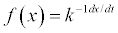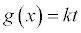Equation Rate-Determining Mechanism Differential Form 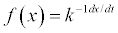Integral Form 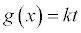EqnNo Diffusion Models         Parabola Law One-Dimensional Diffusion 1/2x x2 D1 Valensi Eqn. Two-Dimensional Diffusion -[ln(1-x)]-1 (1-x)ln(1- x)+ x D2 Jander Eqn. Three-Dimensional Diffusion (3/2)(1-x)2/3[1-(1- x)1/3]-1 [1-(1-x)1/3]2 D3 Ginstling-Brounshtein Eqn. Three-Dimensional Diffusion (3/2)[(1-x)-1/3-1]-1 1-2x/3-(1-x)2/3 D4 Zhuravlevl, Lesokin, Tempelman Eqn. Three-Dimensional Diffusion (3/2)(1-x)4/3[(1- x)-1/3-1]-1 [(1-x)1/3-1]2 D5 Phase Boundary Reaction         Power Law Contracting Cylinder 2(1-x)1/2 1-(1-x)1/2 P1 Power Law Contracting Sphere 3(1-x)2/3 1-(1-x)1/3 P2 Reaction-Order Models         First-order Chemical Reaction (1-x) X R1 Second-order Chemical Reaction (1-x)2 [1/(1-x)]-1 R2 Third-order Chemical Reaction (1-x)3 (1/2)[(1-x)-2-1] R3 Nucleation Models         Mampel power law Nucleation (2/3)x-1/2 x3/2 N1 Mampel power law Nucleation 2x1/2 x1/2 N2 Mampel power law Nucleation 3x2/3 x1/3 N3 Mampel power law Nucleation 4x3/4 x1/4 N4 Exponential law Nucleation X ln x N5 Avrami-Erofeev Eqn. Random Nucleation and Subsequent Growth 2(1-x)[-ln(1-x)]1/2 [-ln(1-x)]1/2 N6 Erofeev Eqn. Random Nucleation and Subsequent Growth 3(1-x)[-ln(1-x)]2/3 [-ln(1-x)]1/3 N7 Prout-Tomkins Ewn. Branching Nuclei x(1-x) ln[x/(1-x)] N8

Table 2: Solid-state reaction expressions examined in this work