 |
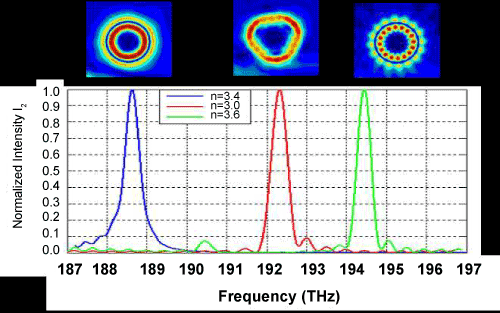
| Figure 8: Spectra of eigenmodes of three SOs with r=1 μm, n=3.4 (blue), 3.0(red) and 3.6 (green). The mode at 188.6 THz is an eigenmode of the SO with r=1 μm, n=3.4 (blue), the mode at 192.2 THz is of the SO with n=3.0,and the mode at 194.4 is the eigenmode of the SO with n=3.6. On top of the peak resonant modes: light intensity resonant inside the SOs at the given frequencies. |