Review Article Open Access
Challenging Conditions to Observe Shear Banding In Highly Entangled Polybutadiene Solutions
Shi-Qing Wang*Morton Institute of Polymer Science and Engineering, University of Akron, Akron, Ohio 44325, USA
- *Corresponding Author:
- Shi-Qing Wang
Morton Institute of Polymer Science and Engineering
University of Akron, Akron, Ohio 44325, USA
Tel: 330-972-7108
E-mail: swang@uakron.edu
Received date: December 07, 2016; Accepted date: March 01, 2017; Published date: March 08, 2017
Citation: Wang S (2017) Challenging Conditions to Observe Shear Banding In Highly Entangled Polybutadiene Solutions. Rheol: open access 1:104
Copyright: © 2017 Wang S. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Rheology: Open Access
Abstract
There is general agreement that the observation of shear banding in well entangled polymer solutions and melts has strong implications for existing models of chain entanglement during large deformation. Understandably, observations of this phenomenon in numerous past measurements have been viewed by some as controversial because of the challenge that these observations raise for the current paradigm of nonlinear polymer rheology. We welcome independent measurements aimed at verifying or refuting the existing conclusions based on carefully prepared, well-characterized and strongly entangled polymer solutions. It is clear that measurements were based on solutions that were either only marginally entangled or polydisperse, which understandably did not exhibit shear banding under the weak shearing conditions that they chose stated “we agree that the sample MW is different from that specified by the supplier and has the Z=22 entanglement number”. But rather than making additional measurements on well entangled relatively monodisperse PB solutions following previous protocols, they continue to speculate that their former measurements were sufficient to demonstrate that shear banding does not exist in highly entangled polymer solutions under all conditions. We find position to be unconvincing and discuss in detail why we reject their conclusions, including a description of why the previous solutions researchers had the correct characterization.
Keywords
Polymer rheology; Shear banding; Polydispersity index; Polybutadiene.
Introduction
Shear banding [1-6] in startup shear of entangled polymer solutions has attracted recent attention from the rheology community. The observation opens a Pondera’s box because shear strain localization makes it ill-defined to carry out traditional rheometric measurements that assume shear homogeneity. Moreover, from the phenomenon emerges the idea of yielding to describe the response of entangled polymers to fast shear. Since 2006, a number of other groups reported shear banding [7-10]. By working with a mischaracterized solution and avoiding the high-shear condition applied to observe shear banding, Li et al. [11] speculated that shear banding may not occur without edge instability. We identified Wang et al. [12] the source of error that caused Li et al. to fail to observe shear banding. Li et al. [13] raised additional questions during their rebuttal that deserved to be examined. We address these questions in this paper.
We first note Li et al. acknowledgement [13] that the molecular weights Mw and molecular mass distributions (as characterized by the polydispersity index, PDI) reported in their original paper [11] were incorrect. Table 1 of Li et al. [13] provide the revised values as well as their previous values. The 1M 10% PB solution of Li et al. [11]) has half or less of entanglements per chain1 relative to most of the PB solutions that were found to show shear banding. Their 1.4 M 10% and 1.4 M 15% solutions have PDIs of 1.8, which is much larger than the PDI~l.03 in most of the PB solutions that we previously reported to show shear banding upon startup continuous shear and non-quiescent relaxation after step-strain.
As indicated in Table 1 of Li et al. [13] out of the eight highly monodisperse samples previously studied with particle-tracking velocimetry (PTV), seven had 40 or more entanglements per chain (Z). One had Z=27. Li et al. reported [11] that they had prepared similarly entangled PB solutions, i.e., Z ≤ 40 with sufficiently low PDI. Li et al. corrected [13] this claim, stating “in re-examining our dynamic data and comparing with the analysis in Wang et al. [12], we agree that the sample MW is different from that specified by the supplier and has the Z=22 entanglement number”. Their samples actually either had Z=20 or PDI around 1.8. It thus turns out that Li et al. [13] samples were not in a regime for shear banding. Since their measurements were not in a regime where shear banding was reported, Li et al. [13] PTV observations do not contradict previous reports of shear banding. They indicated that they “were unable to reproduce any of the observations of Wang and coworkers regarding strain localization and banding in entangled polymers”. Given the characteristics of their samples, we can only expect homogeneous shear, as emphasized by Wang et al. [12].
Shear banding occurs during startup shear if only the PB solutions are sufficiently entangled with narrow molecular weight distribution and sheared at rates deep inside the shear banding regime, mapped out by the “phase diagram” published in Ref. [14]. Wall slip needs to be minimized for a given sample by applying apparent Weissenberg number Wiapp that well exceeds the borderline Wiws-bnl given by:

which is equation 2 in Ref. [14], where bmax is the extrapolation length for full wall slip at the stress plateau. Below Wiws-bnl, in presence of massive wall slip, i.e., for bmax/H>>1, startup shear with a larger only results in more severe wall slip so that the bulk remains weakly sheared. The local shear rate in the bulk stays as low as the reciprocal terminal relaxation time as long as Wiapp<Wiws-bnl, where the subscript “ws-bnl” stands for wall slip to bulk nonlinear response. Although shear banding is not due to edge instability, it is helpful to find a means to eradicate edge effects, as done in Ref. [6]. Below we review key steps necessary to observe shear banding by commenting on the previous unsuccessful investigation of Li et al. [13].
Sufficiently Entangled and Monodisperse Samples are Essential for the Study of Shear Banding and This was not the Case in the Measurements of Li et al. [11]
Insufficient entanglement of 1 M 10% PB solution of Li et al. [11]
In absence of a comparable PB solution to verify or falsify the occurrence of shear banding during startup continuous shear and nonquiescent relaxation after a large stepwise shear; Li et al. insisted that their 1 M 10% PB solution is still entangled enough. How can a 10% PB solution Z ≤ 20 startup-sheared at Wi=4.8 be compared to a 10% PB solution with Z=27 at Wi=13? We suggest that Li et al. [11] prepare comparable solutions2 and apply sufficiently high Weissenberg number Wi if they want to investigate shear banding.
1.4 M 10% and 1.4 M 15% PB solution of Li et al. [11] are polydisperse and never sheared with high Wi in startup shear
The two PB solutions, based on the parent 1.4 M PB obtained from Polymer Source Inc. as P10053-Bd, turned out to have a rather high PDI of 1.8. Moreover, the highest value of Wi used by Li et al. [13] for startup shear was less than Wi=15. The “phase diagram” (or more precisely, the rheological-state diagram since the word ‘phase’ could cause some confusion if taken too literally) is only a qualitative roadmap in the absence of a fundamental theory of shear banding. For maximal accuracy, this prescription of different rheological state under steady shear was proposed for monodisperse and highly entangled polymer samples, for which Wi can be well defined. For polydisperse systems, Wi is not well defined. We maintain that Li et al. [11] belief that they had entered “well into the phase diagram” is unwarranted.
General conclusion about shear banding is unsupported by observations
A necessary condition for shear banding is sufficient chain entanglement. Polydispersity plays an adversary role. Thus, Z and PDI are two implicit variables in the phase diagram. Since there is only empirical and qualitative information about what values of Z and PDI are required respectively and in combination to observe shear banding, it is necessary to go to the interior of the phase diagram instead of staying at the borderlines between homogenous shear and strain localization. As stated in the Summary/Conclusion section by Li et al. [13], “to further address the shear banding problem, it is suggested that a sample with a higher MW or concentration be tested at a higher Wi in the future.” Indeed, this should have been the most essential conclusion. We add that such a future study must first overcome experimental difficulties such as edge fracture.
Edge Effects must be dealt with
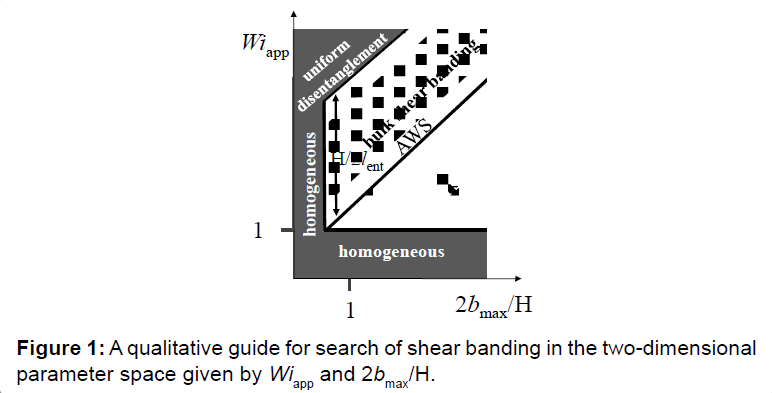
Studies of strongly nonlinear responses in a conventional rheometric setup have been plagued by edge instabilities. In other words, edge effects have limited our ability to probe the deeply nonlinear regime [15] We dealt with the issue of edge fracture from the onset [16]. Wang et al. indicated [14] in Section 3 that reliable rheometric measurements can be obtained free of edge fracture, as demonstrated by Ravindranath and Wang [6] using the home-designed CPP apparatus. Edge effects take time to accumulate. Prolonged shear can avoid edge fracture when the meniscus is wrapped by a flexible film. Such a method allowed Ravindranath et al. [4] to apply high values of Wi to well-entangled monodisperse PB solutions and to reveal shear banding. To verify or falsify these previous PTV observations, Li et al. [13] need to adopt similar or more effective means to insulate the simultaneous PTV and rheometric measurements from any influence of edge fracture. No direct experimental evidence was supplied to show that bulk shear banding can be initiated or created by edge fracture, which was also argued by [17, 18] to be the origin of the entanglementdisentanglement transition [6,16] (Figure 1).
There are a number of cases where shear banding is made to disappear without lowering the level of chain entanglement, i.e., the magnitude of plateau modulus, deep inside the shear banding regime where edge effects and other speculative factors should have produced shear banding according to Li et al. [13] We also note that for a given shear rate to produce a startup shear non-quiescent relaxation is observed to occur after shear cessation at γ1 (>1). The same startup shear does not produce any shear strain localization at a shear strain appreciably beyond the yield strain γy at the stress overshoot where γy can be many times higher than γ1. These two facts contradict the speculation that non-quiescent relaxation arises from edge effect.
The “Phase Diagram” of Wang et al. [14] is not a Quantitative Target
There is significant misunderstanding of the rheological-state diagram in terms of its origin, character and function. The original question was whether shear banding is a physical property of well entangled polymer solutions and not whether the phase diagram is quantitatively accurate or not. Most of the space in Li et al. [13] was used to argue that the data of Li et al. [11] did not fit the phase diagram quantitatively. As emphasized by Wang et al., the phase diagram in Ref. [14] qualitatively depicts the steady-state shear field following a startup continuous shear. The diagram was constructed based on scaling arguments. Wang et al. [12] emphasized that homogeneous shear may be expected “when an entangled polymer solution is not strongly entangled.” Wang et al. [14] repeated emphasized the requirement that solutions be “well-entangled”: “Both (a) and (b) of Figure 2 serve as a roadmap for the steady-state behavior of well-entangled polymers in startup shear” [14]. Figure 1 is a revised plot to emphasize that near the borderline at Wiws-bnl it is more likely to observe apparent wall slip (AWS).
PTV observations of step-strain tests examine whether measurable motions occur after termination of homogeneous stepwise shear. We can construct another rheological-state diagram for step-strain tests. Such a diagram should be a 3D plot, because it requires the strain amplitude γ0 as a third parameter. We find that non-quiescent relaxation occurs only when γ0 is beyond a threshold. In absence of the corresponding stress versus time information and video recording of the entire process, it is unclear why Li et al did not observe nonquiescent relaxation since Li et al. [11] used what appears to be a sufficiently large γ0=3.6.
Regarding Previous Samples Studied at Akron
Ravindranath et al. [3] used a polybutadiene with high vinyl content, labeled as PBD-1.8 K as the solvent, to prepare a 1 M 10% PB solution [3] Since PBD-1.8 K has a viscosity of 97 Pa.s, significantly higher than PBD-15 K, this 1 M (10%)-1.8 K indeed had τ=286, several times higher than τ of 1 M (10%)-15 K. It is surprising that Li et al. [13] casted doubt on this solution before figuring out why this solution should have a much higher relaxation time due to the far more sluggish solvent. Here we followed the notation of Ravindranath et al. [3] when referring the samples in question. All the necessary information was provided in Tables 1 to 3, originally from Ref. [3]. A second example is a 0.7 M (5%)-1.8 K, labeled as 0.7 M (5%)-2 K in Ref. [4], which has a considerably higher τ than 0.7 M (10%)-9 K. A third solution made with this 1.8 K oligomeric PB is a 3% PB solution based on this PBD-1.8K that is nearly 10 times more sluggish at 10°C than a 3% PB solution based on a PBD-9 K, as shown in Ref. [19].
| Sample | Mn (g/mol) | Mw (g/mol) | Mw/Mn | Source |
|---|---|---|---|---|
| 1 M | 1.014ÃÂ?106 | 1.052ÃÂ?106 | 1.03 | University of Akron |
| 0.7M | 0.74ÃÂ?106 | 0.75ÃÂ?106 | 1.02 | Bridgestone |
Table 1: Molecular characteristics of long chain PBDs.
| Sample | Mn (g/mol) |
Mw (g/mol) |
Mw/Mn | Source | Â Â Â Â Â hs (Pa.s) |
|---|---|---|---|---|---|
| PBD-15K | 14020 | 15000 | 1.07 | Bridgestone | 36 |
| PBD-1.8K | 1800 | - | - | Sigma-Aldrich Cat. No. 20,043-3 |
97 |
| oil (DTDP) | 530 | 530 | 1 | Imperial oil | 0.2 |
Table 2: Molecular characteristics of various solvents.
| Solution | Mw/Me | t (s) | tR (s) | η (Pa.s) | η/ηs | lent (nm) | b (mm) |
|---|---|---|---|---|---|---|---|
| 1M(10%)-DTDP | 40 | 18.3 | 0.45 | 60,484 | 302,420 | 17 | 5.1 |
| 1M(10%)-15K | 40 | 66.6 | 1.66 | 2.5ÃÂ?105 | 6,944 | 17 | 0.12 |
| 1M(10%)-1.8K | 40 | 285.7 | 7.14 | 1.25ÃÂ?106 | 12,886 | 17 | 0.22 |
| 0.7M(5%)-DTDP | 13 | 1.25 | 0.096 | 773 | 3,865 | 27 | 0.10 |
Table 3: Properties of PBD solutions.
Previous studies of Struglinsky and Graessaley and Watanabe et al. [20,21] have demonstrated that the terminal relaxation time τ in entangled binary mixtures could be insensitive to the composition because of a subtle cancellation. Thus, 1 M (10%)-9 K and 1 M (15%)- 9 K had comparable τ in Ref. [4]. Similarly, Table 2 of Ravindranath and Wang (listed 1 M (10%)-15 K and 1 M (15%)-15 K to have 71 and 83 s respectively for τ, again rather similar values. Contrary to Li et al. [13], it is therefore incorrect to assert that “the Wang group has some inconsistencies in the characterization of the linear viscoelastic properties of their polytubadiene samples.”
Other Clarifications
Data outside purple rectangle
Wang et al. [14] concentrated on reaching the shear banding regime at sufficiently high Wi beyond the wall slip-dominant regime. Li et al. (2014) cited Ravindranath and Wang [6] as observing shear banding at Wi=16 for M (10%)-1.5 K (for which the dominant character was actually massive wall slip) and Wi=10 for 1 M (10%)-5 K and wondered why their own 1 M 10%-1.5 K and 1.4 M 10%-9 K did not show any strain localization at Wi=4.8 and 9.4 respectively. The answer is that Ravindranath and Wang [6] had Z=40 and PDI=1.03 whereas Li et al. [11] mischaracterized their 1M 10% solution and had either Z ≤ 20 or PDI=1.8. No comparison can be made here. We also note that a previous PTV study reported the recovery toward homogeneous shear beyond the shear banding regime at higher rates, as shown in Figure 2. Had edge instability caused shear banding, should not there be stronger shear banding at the higher rate?
Surface condition
Wang et al. [14] discussed in detail the relation between wall slip and bulk shear banding Wang et al. [12] explicitly notes that previous PTV studies of well entangled PB solutions did not require any surface treatment because the solutions were made using polymeric solvents to suppress the inherent ability of the solutions to undergo measurable wall slip. Wang et al. [12] did not “suggest that surface treatment is irrelevant to the problem”, as Li et al. [11] claimed. In fact, the boundary condition that can be affected by surface treatment is crucially relevant to the problem.
Imaging issues
The CPP/PTV setup [6,22] requires the video-camera to peek into an optical window at an angle. We always verified that the PTV setup worked properly by showing that the initial velocity profile was linear, as shown in Ref. [6] and Ref. [22]. This point was emphasized in V.B of Wang et al. [12]. The situation depicted by Li et al. [13] did not occur in these past studies. Ironically, the speculation of Li et al. would apply equally to the two PTV setups of Li et al. [11].
Moreover, Ravindranath et al. [3] carried out the PTV observations by placing the video-camera horizontally, with the objective lens focused onto a laser-illuminated plane well inside the shear cell through a transparent film. This setup is free of the potential effects hypothesized by Li et al. [13].
Asymmetric boundaries
We have rarely observed symmetric shear banding in entangled PB solutions although it could happen [4] when using parallel-disks. The symmetry breaking has an unknown origin at the present time. The fast shear band is typically situated next to the moving surface of higher surface energy although the opposite case has also been reported in Ravindranath and Wang [6]. In our CPP/PTV setup, the stationary plate has an optical window of a small area. No physics tells us that (a) bulk shear banding would arise and grow along the velocity gradient direction from a wall/polymer interface and (b) asymmetric boundary conditions would be the cause of shear banding. We have made a special-designed counter-rotating parallel-disk shear cell to remove asymmetry. As shown in the PTV movie, a DNA solution (11 mg/mL) studied in Ref. [23] shows symmetric shear banding when sheared at apparent rate of 0.2 s-1 in the counter-rotating device.
Regarding step strain
Most of the previous observations of non-quiescent relaxation involved well entangled monodisperse PB solutions, stepwise sheared at very high values of Wi. It is questionable for Li et al. [13] to quote the testing condition for a styrene-butadiene copolymer melt to validate their step-strain condition because the SBR melt was super-glued onto the shearing plates to prevent wall slip [5].
Further Disagreements with Li et al. [13]
The last paragraph of V.D in Li et al. [13] speculates whether wall slip causes shear banding. Given that the spatial resolution of the current PTV is on the order of 10 μ, it is not possible to distinguish true wall slip involving a monolayer of disentangled chains from a thin shear band of high shear rate. In many of our previous publications, we deduced that a high shear band was present at the shearing surface because the apparent extrapolation length was much higher than bmax. In presence of such apparent wall slip the bulk was saved from undergoing a high rate of shear. Based on our understanding and extensive experiences, suppression of wall slip by improving the surface/polymer interactions always maximizes the condition for shear banding. Thus, we cannot agree with the idea that somehow suppression of wall slip would prevent shear strain localization, as implied in the concluding paragraph of Li et al. [13]
Li et al. [13] stated “Li et al. [11] demonstrate that edge effects can cause apparent shear banding”. They saw shear banding when edge fracture was present. Such an observation is not a demonstration that the shear banding was caused by edge effects. Li et al. [11,13] had neither experimental evidence nor theoretical argument to delineate how edge effects can produce shear banding. In contrast, we have discussed [14,24,25] the fundamental physics that explain the emergence of shear banding and wall slip respectively in terms of localized yielding through chain disentanglement upon force imbalance between the intermolecular potential barrier and entropic retraction force.
There was no evidence that previous PTV observations of nonquiescent relaxation [3,5] involved misalignment. Ravindranath et al. showed with the same setup that the characteristics of entangled polymers including bmax/H systematically dictate how non-quiescent relaxation takes place [25].
Li et al. speculate that other instabilities could be the cause of shear banding. However, there is neither experimental evidence nor analytical understanding to support such speculations as “instability could develop near the surfaces and propagate into the bulk” Li et al. [13] and “this leads to an irregular flow field near to the sample edge which propagates slowly inwards toward the center of the sample and distorts the velocity field, perhaps randomly” Li et al. [11] Since they have never performed these experiments, how did they know that such propagation actually took place? Li et al. [13] states “we postulate that due to the presence of normal forces and the irregularity of wall slip behavior near the clearance, it is reasonable to speculate that secondary flows should exist at or near the clearance in CPP-type geometries.” How do they know that “irregularity of wall slip behavior in the clearance” took place since they did not perform any tests in CCP-type geometries? Without experimental evidence, speculations of Li et al. [11,13] remain as mere speculation.
Conclusion
Shear banding occurs during startup shear at sufficiently large values of Wi presumably because of localized yielding of the entanglement network [24]. The microscopic yielding would not take place if wall slip dominates the stress response. Only at sufficiently high rates, the bulk can undergo strong shear. The subject of wall slip must be fully comprehended before we can investigate bulk behavior such as shear banding. Moreover, when there is insufficient entanglement, yielding does not localize, and shear banding would not be observable. Non-quiescent relaxation3 is presumably due to elastic yielding and has nothing to do with edge effects because it occurs after shear cessation from a moderate strain magnitude. Its observation also requires that the chain entanglement is of a sufficiently high level, and magnitude of step strain is beyond a threshold.
Li et al. [11] used mischaracterized polybutadiene (PB) solutions that were not the same as those studied in the literature. They did not apply comparably high Weissenberg number Wi in their search for shear banding. Their wandered at the borderline between wall slip and banding instead of entering deep into the shear banding dominant regime. Consequently they avoided the challenge to remove the influence of edge instability as Ravindranath and Wang [6] did. Therefore, Li et al. [11] measurements did not test the reproducibility of the shear banding observations. Li et al. [13] had no experimental basis for their suggestion that “the shear banding observed in Ravindranath and Wang [3], Ravindranath and Wang [6], Ravindranath et al. [4] and Boukany and Wang [5] may be due to experimental artifacts rather than to a material nonlinearity induced instability.” It is particularly non-scientific for them to mention the studies [26,27] of Boukany et al. that were based on DNA solutions that they did not work with and were too soft to show any edge effects.
Concerning the emergence of strain localization, there are several outstanding questions that future studies need to resolve:
(1) Do shear banding and non-quiescent relaxation exist in other polymer solutions besides polybutadiene solutions?
(2) If strain localization is confirmed, what causes it? Here one needs to understand the physics behind such behavior t.
(3) Why would strain localization occur in well-entangled polymers?
This is related to the question of whether well-entangled polymers behave like solids and how they undergo yielding. In our current modeling of this complex phenomenon, shear banding and nonquiescent relaxation are both results of localized yielding, due to molecular force imbalance [24]. Although yielding is an unfamiliar concept in the field of polymer melt rheology, such a proposal was actually made long ago by Maxwell and Nguyen. The latest evidence of localized yielding came from the PTV observations of shear strain localization at the die entry during extrusion of polymer melts into a channel die [28] It involved a closed system, i.e., there was no free surface or edge to be concerned with.
(4) What are the theoretical and practical significances of the strain localization phenomena?
In our view, they are the cause of gross and surface melt fracture, i.e., gross extrudate distortion and sharkskin like extrudate surface roughness respectively. They have prompted us to realize that a different picture [24,29] is necessary to describe nonlinear responses of entangled polymeric liquids to fast large deformation of either shear or extension.
It is scientifically healthy to test the reproducibility of previous particle-tracking velocimetric (PTV) observations of shear strain localization since these findings have radically altered our understanding of nonlinear rheological behavior of entangled polymers [30,31]. Moreover, similar PTV studies should be carried out based on other polymers such as polyisoprene and polystyrene solutions. Given the incomplete empirical knowledge about the requirements in terms of specific values of Z and PDI necessary to observe strain localization, additional objective, careful and systematic PTV studies are desirable in the future.
This work is supported, in part, by the National Science Foundation (DMR-1105135).
1Li et al. [13] provided an incorrect description of the number entanglements per chain, Z' for the 1M 10% solution in Li et al. [11] because Li et al. [11] misused the information provided by Wang et al. [12] that stated that the GPC on a recent order of P10053-Bd from Polymer Source Inc. (PSI) yielded only Mw=660 kg/mol instead of the advertised value of 1.4*103 kg/mol. (a) We never reported 560 kg/mol as quoted by Li et al. [13] (b) There is no logic to use our GPC result of P10053-Bd as the estimated molecular weight for their 1 M PB sample because Li et al. [11] ordered P10053-Bd from PSI to prepare their 1.4 M PB solutions and P9762-Bd from PSI to make the 1 M 10% solution. (c) It is also uncertain that the 1.4 M PB solutions had the parent PB with Mw=1.4*103 kg/mol.
Since the relaxation time (Z') of 1 M 10% in Li et al. [11] is 1.4 s, we could try to estimate Z' according to (Z=40)/(Z')=15.6/1.4=(40/Z')3~3.4, where (Z=40)=15.6 s is from Ravindranath and Wang [6]. Thus, we have Z' ranging from 18 to 20, not 22 as assigned by Li et al. [13].
2 If one is looking for shear banding instead of wall slip using PTV with video capture rate of 30 fps, it is advised that a 1 M 10% PB solution be made with oligomeric PB of significantly higher molecular weight than 1.5 K, as was done in most of the past PTV studies. Ravindranath and Wang [6] studied 1 M 10%-1.5 K only because they need to compare with an earlier study of Tapadia and Wang [16] that was based on 1 M 10%-1.5 K.
References
- Tapadia P, Wang S-Q (2006) Direct Visualization of Continuous Simple Shear in Non-Newtonian Polymeric Fluids. Phys Rev Lett 96: 016001.
- Wang S-Q, Ravindranath S, Boukany P, Olechnowicz M, Quirk RP, et al. (2006) Nonquiescent Relaxation in Entangled Polymer Liquids after Step Shear. Phys Rev Lett 97: 187801.
- Ravindranath S, Wang S-Q. (2007) What Are the Origins of Stress Relaxation Behaviors in Step Shear of Entangled Polymer Solutions? Macromolecules 40: 8031-8039.
- Ravindranath S, Wang S-Q, Ofechnowicz M, Quirk RP (2008) Banding in simple steady shear of entangled polymer solutions. Macromolecules 41: 2663-2670.
- Boukany PE, Wang S-Q, Wang X (2009) Step Shear of Entangled Linear Polymer Melts: New Experimental Evidence for Elastic Yielding. Macromolecules 42: 6261-6269.
- Ravindranath S, Wang S-Q (2008) Steady state measurements in stress plateau region of entangled polymer solutions: Controlled-rate and controlled-stress modes. J Rheol 52: 957-980.
- Fang Y, Wang G, Tian N, Wang X, Zhu X, et al. (2011) Shear in homogeneity in poly(ethylene oxide) melts. J Rheol 55: 939-949.
- Hu YT (2010) Steady-state shear banding in entangled polymers? J Rheol 54: 1307-1323.
- Hu YT, Wilen L, Philips A, Lips A (2007) Is the constitutive relation for entangled polymers monotonic? J Rheol 51: 275-295.
- Jaradat S, Harvey M, Waigh TA (2012) Shear-banding in polyacrylamide solutions revealed via optical coherence tomography velocimetry. Soft Matter 8: 11677-11686.
- Li YF, Hu M, McKenna GB, Dimitriou CJ, McKinley GH, et al. (2013) Flow field visualization of entangled polybutadiene solutions under nonlinear viscoelastic flow conditions. J Rheol 57:1411-1428.
- Wang S-Q, Liu G, Cheng S, Boukany PE, Wang Y, et al. (2014) Letter to the Editor: Sufficiently entangled polymers do show shear strain localization at high enough Weissenberg numbers. J Rheol 58: 1059-1069.
- Li YF, Hu M, McKenna GB, Dimitriou CJ, McKinley GH, et al. (2014) Response to: Sufficiently entangled polymers do show shear strain localization at high enough Weissenberg numbers". J Rheol 58: 1071-1082.
- Wang S-Q, Ravindranath S, Boukany P (2011) Homogeneous shear, wall slip, and shear banding of entangled polymeric liquids in simple-shear rheometry: A roadmap of nonlinear rheology. Macromolecules 44: 183-190.
- Pattamaprom C, Larson RG (2001) Constraint release effects in monodisperse and bidisperse polystyrenes in fast transient shearing flows. Macromolecules 34: 5229-5237.
- Tapadia P, Wang S-Q (2004) Nonlinear Flow Behavior of Entangled Polymer Solutions: Yield like Entanglement−Disentanglement Transition. Macromolecules 37: 9083-9095.
- Inn YW, Wissbrun KF, Denn MM (2005) Effect of edge fracture on constant torque rheometry of entangled polymer solutions. Macromolecules 38: 9385-9388.
- Sui C, McKenna GB (2007) Instability of entangled polymers in cone and plate rheometry. Rheol Acta 46: 877-888.
- Li X, Wang S-Q (2010) Elastic yielding after step shear and during LAOS in the absence of meniscus failure. Rheol Acta 49: 985-991.
- Struglinski MJ, Graessley WW (1985) Effects of polydispersity on the linear viscoelastic properties of entangled polymers.1. Experimental observations for binary mixtures of linear polybutadiene. Macromolecules 18: 2630-2643.
- Watanabe H, Sakamoto T, Kotaka T (1985) Viscoelastic properties of binary blends of narrow molecular weight distribution polystyrenes. 2. Macromolecules 18: 1008-1015.
- Cheng S, Wang S-Q (2012) Is shear banding a metastable property of well-entangled polymer solutions? J Rheol 56: 1413-1428.
- A PTV movie capturing startup shear of DNA-glycerol solution at concentration 11 mg/mL and a shear rate 0.2 (1/s) using a special-desigened counter-rotating device fit onto MCR 301 rotational rheometer at room temperature, made at University of Akron by Pouyan Boukany, USA.
- Wang S-Q, Ravindranath S, Wang Y, Boukany P (2007) New theoretical considerations in polymer rheology: Elastic breakdown of chain entanglement network. J Chem Phys 127: 064903.
- Ravindranath S, Wang S-Q, Olechnowicz M, Chavan V, Quirk R (2011) How polymeric solvents control shear inhomogeneity in large deformations of entangled polymer mixtures. Rheol Acta 50: 97-105.
- Boukany PE, Wang S-Q (2009) Shear banding or not in entangled DNA solutions depending on the level of entanglement. J Rheol 53: 73-83.
- Boukany PE, Wang S-Q (2009) Exploring the transition from wall slip to bulk shearing banding in well-entangled DNA solutions. Soft Matter 5: 780-789.
- Zhu X, Yang W, Wang S-Q (2013) Exploring shear yielding and strain localization at the die entry during extrusion of entangled melts. J Rheol 57: 349-364.
- Wang S-Q, Wang Y, Cheng S, Li X, Zhu X, et al. (2013) New experiments for improved theoretical description of nonlinear rheology of entangled polymers. Macromolecules 46: 3147-3159.
- Wang S-Q (2015) Nonlinear rheology of entangled polymers at turning point. Soft Matter 11: 1454-1458.
- Wang S-Q (2017) Nonlinear polymer rheology: Macroscopic phenomenology and molecular foundation. New York: Wiley.
Relevant Topics
Recommended Journals
Article Tools
Article Usage
- Total views: 2888
- [From(publication date):
March-2017 - Aug 31, 2025] - Breakdown by view type
- HTML page views : 1993
- PDF downloads : 895