Research Article Open Access
Computer Simulation of Blood Flow with Nanoparticles in a Magnetic Field as a Third Grade Non-Newtonian Through Porous Vessels by Flex PDE Software
Akbari N1, Ganji DD2*, Gholinia M3 and Gholinia S21Shahid Sattari Aeronautical University of Science and Technology, Tehran, Iran
2Department of Mechanical Engineering, Babol University of Technology, Babol, Iran
3Department of Mechanical Engineering, Science and Technology University, Babol, Iran
- *Corresponding Author:
- Ganji DD
Department of Mechanical Engineering
Babol University of Technology, P.O. Box 484
Babol, Iran
Tel: +98 111 32 34 501
E-mail: ddg_davood@yahoo.com
Received date: March 21, 2017; Accepted date: April 20, 2017; Published date: April 27, 2017
Citation: Akbari N, Ganji DD, Gholinia M, Gholinia S (2017) Computer Simulation of Blood Flow with Nanoparticles in a Magnetic Field as a Third Grade Non-Newtonian Through Porous Vessels by Flex PDE Software. Innov Ener Res 6:160.
Copyright: © 2017 Akbari N, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Innovative Energy & Research
Abstract
In this paper, we used Flex-PDE software to study the blood flow with nanoparticles in a magnetic field as a third grade non-Newtonian through porous vessels. Viscosity of Nano fluid is clear via Constant, Vogel’s and Reynolds’ patterns. The performance of Flex-PDE software is briefly raised and employed to derive solution of nonlinear equations. Attempts are performed in order to indicate the validity and performance of the present software in comparison with Collocation Method (CM). Comparison between the Flex-PDE software and analytical conclusions of the issue, illustrates excellent complying in solving this nonlinear differential equation. As well as, in the present perusal, the impact of various physical parameters like: Grashof number, pressure gradient, thermophoresis parameter, Brownian motion parameter and magnetic field intensity on concentration, velocity and temperature profiles are examined. Conclusions displays that velocity profile has direct relationship with thermophoresis parameter Nt but Brownian motion Parameter Nb has reverse relationship with velocity profile V(r). In addition, this study illustrate that Flex-PDE is strong software to solve nonlinear differential equations, such as the issue introduced in this research.
Keywords
Porous vessels; Flex-PDE software; Collocation Method (CM); Magnetic field
Introduction
The study of non-Newtonian fluids has become important in the past two decades and this is mainly due to the widespread use of this fluid. The recent advances in nanotechnology have led to develop a new group of technology in heat transfer named Nano fluids, as far as the study in the field of Nano fluids has found very broad dimensions. Particularly, these fluids are used in industrial applications such as glues, coal slurries, biological solutions, polymers solution or melts, asphalts, paints, greases and lubricant, cooling issues, filtration practice and hydrocarbon oils etc. [1-7]. However, on the one hand, researchers are pursuing the preparation and manufacturing of Nano fluids with variety of nanoparticles and nanotubes having different size distributions, regarding increasing of thermal conductivity and heat transfer of fluids; while, some of the researchers are dealing with investigating the issue of stability and non-settling of nanoparticles during the heat transfer process and the lack of agglomeration or migration of them. However, close examination of sources shows that a very little attention is paid to the non-Newtonian Nano fluids (proportional to the extent of the ability of the fluid) [8].
Human blood is a combination of white blood cells, red blood cells, and platelets in a fluid called plasma, which contains organic and mineral salts and protein. According to the high volumetric percentage of red blood cells relative to other particles (97%), physically the blood behavior is mostly similar to the red cells and proteins of the plasma. The plasma has a Newtonian behavior; however, the blood shows equivalent non-Newtonian behavior of shear thinning with increasing of shear rate and reduction in viscosity, so that sometimes the viscosity changes up 5 to 10 times. However, it is almost constant in high shear rates and the blood has a behavior similar to Newtonian fluids. Now, studies in this area have found very broad dimensions. Ogulu and Amos [9] created the pulsatile blood flow model using the Navier- Stokes equation in the cardiovascular system and found that with increasing porosity of the medium, an increase in the wall shear stress is observed. Nandakumar et al. [10] the effects of Reynolds number (Re) and percentage stenosis on steady flow, and Womersley number (Wo) on pulsatile flow, of blood via a two-dimensional channel with stenosis are considered. Their outcomes illustrate that applying a Newtonian model will explain reasonably accurate conclusions for plaque growth in aorta-sized vessels and wall shear stress. Moyers- Gonzalez et al. [11] on the designing of oscillatory blood flow in a pipe, observed that by increasing frequency of the (constant amplitude), shear stress, the top amounts of the velocity field and pressure gradient oscillations decreases. Recently, Srinivas et al. [12] the flow and heat transfer of blood carrying gold nanoparticles in a porous channel with moving/stationary walls in the attendance of thermal radiation are studied. They applied the Homotopy Analysis Method (HAM) to solve governing equations of blood carrying gold nanoparticles. In an empirical study Sinha et al. [13] investigated concerning the impact of externally imposed periodic body acceleration on the flow of blood by taking into account the slip velocity at the wall of the artery and blood as a non-Newtonian fluid through a time-dependent stenosed arterial segment. Many researches are focused on second and third grade non- Newtonian fluids which some of them are introduced in this article. Solution and modeling of the unsteady flow of an incompressible third grade fluid within a porous medium aboard a porous sheet is analyzed by Aziz and Aziz [14]. They assumed that the fluid is electrically conducted used transversely to the flow in the attendance of a uniform magnetic field. Flow analysis and heat transfer for blood conveying gold nanoparticles as a third degree non-Newtonian in porous medium with attendance of magnetic field are simulated by Hatami et al. [15]. Baoku et al. [16] studied the influence thermos physical parameters and third degree, partial slip on the steady flow, heat and mass transfer past of an infinite vertical insulated plate of viscoelastic third degree fluid expose to suction throughout the boundary layer. Moreover, many scholars examined on non-Newtonian Nano fluids and their applications on the blood field and other [17-19]. In this paper, we have applied Flex PDE software to find the solution of nonlinear differential equations governing the blood flow with nanoparticles in a magnetic field as a third grade non-Newtonian through porous vessels. As well as, the concentration, velocity and temperature profiles are shown and the impact of Grashof number, pressure gradient, thermophoresis parameter, Brownian motion parameter and magnetic field intensity are studied. The acquired results from Flex-PDE software are compared with those of acquired from Collocation Method (CM) to check the precision of the explained Solution. Method (CM) is an efficient manner based on the trial Function that is for study of nonlinear issues. The comparison of the conclusion of Flex-PDE software and Collocation Method (CM) illustrate excellent complying in solving this nonlinear issue.
Problem Description
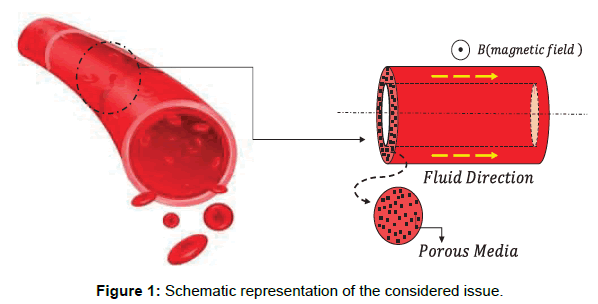
Consider a porous artery containing steady, incompressible, non- Newtonian Nano fluid in presence of a magnetic field. The outline and coordinates of the issue are presented in Figure 1 in order to have a better understanding. In this paper, the blood flow is designed as the one-dimensional issue. Although blood flow is a three-dimensional problem, its modeling is currently not possible regarding the long computation time that is required to model the vascular network as well as the fluid-solid interaction between the blood and the vessel wall. As well as, the blood is considered as a third-grade non-Newtonian fluid containing nanoparticles. The governing boundary layer equations acquired by Rahbari et al. [20], as systems of nonlinear ordinary differential equation are given by:
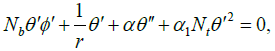 (1)
(1)
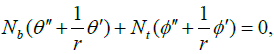 (2)
(2)
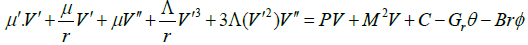 (3)
(3)
The boundary conditions are [20]:
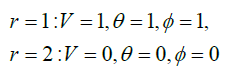 (4)
(4)
Where ‘prime’ denotes differentiation with respect to r. Nb, Nt, M, C and Gr Parameters are Brownian motion parameter, thermophoresis parameter, MHD parameter, pressure gradient and Grashof number, respectively.
This problem for three case of μ has been examined
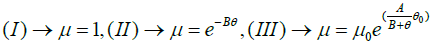 (5)
(5)
Mathematical Procedures
In this section two solution have been examined for solve differential equation:
Flex-PDE software
Flex-PDE is unique software to build and perform multiple analyses of mathematical models of real systems and patterns and to identify and describe the problems and their performance. This software is able to produce statistical model from different data in the fields of physics, mechanics, electromagnetics, chemical reactions, particle emissions, etc. and to address the analysis of models behavior and stress in a structured environment in the form of 1D, 2D and 3D. Numerous articles in various fields of non-Newtonian Fluids have been given by this software [21,22].
Some features of this software are including:
• Build and analyze mathematical models from real systems.
• Use from dependence equations, differential, and integral for modeling.
• The possibility of customizing models and graphs and annotating on them.
• Solving several nonlinear complex equations, simultaneously.
• The ability to descriptive analysis of equations.
Boundary conditions section
In this software, boundary conditions are applied when specifying the problem boundaries. The primary kinds of boundary conditions are boundary are VALUE and NATURAL. VALUE boundary conditions define the amount of a variable on the boundary of the domain, NATURAL boundary conditions define the amount of a variable on the boundary of the domain, NATURAL boundary conditions define the value of charge on the boundary of the domain problem definition is divided into diverse parts in Flex PDE software.
Accuracy control section
The tolerance in this software is named ERRLIM which is adjusted in the SELECT part in the text. This command tells the Flex-PDE to break any cell for which the error of the consistency study is more than 0.001% and perform out the solution again. The advantage of this software is that it amends the grid twice. This means that Flex- PDE has a high consistency with the numerical solution. In this paper, we compare the conclusions of Flex-PDE software with obtained conclusions from CM and by writing Flex-PDE software codes for Eqs. (1) and (3). This table is parts of the Flex-PDE software codes. For guidance of codes written in this article.
Collocation Method (CM)
Weighted residual manner was first introduced by Ozisk [23] to solve the differential equation in heat transfer; Galerkin and Collocation manner are analytical methods that are based on the weighted residual manner. In Collocation Method, a trial family of approximate solution T, containing a finite number of undetermined coefficient C1, C2,… and Cn can be constructed by the superposition of some basic functions like polynomials, the trial solution and trigonometric functions is so selected that it satisfies the essential boundary conditions for the issue. Hereupon, the issue of constructing an approximate solution becomes one of determining the unknown coefficients C1, C2, … and Cn. Thus, the residual stays close to zero throughout the domain of the solution.
Application of Described Software and Method in the Issue
Flex-PDE software
Parts of Flex-PDE software code: Title Computer Simulation of blood flow with nanoparticles in a magnetic field as a third grade non- Newtonian through porous vessels. Coordinates cartesian1 Variables V, ϴ, ɸ.
Definitions:
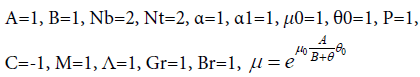
Equations:
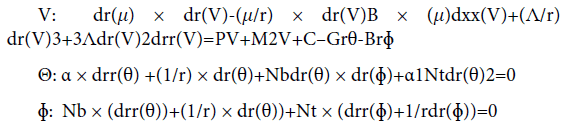
Boundaries:
Region 1 start (1) Point value (V)=1 Point value (θ)=1.
Point value (ɸ)=1 Line to (2) Point value (V)=0 Point load (θ)=0 Point value (ɸ)=0.
Plots Elevation (V) from (1) to (2).
Elevation (θ) from (1) to (2) Elevation (ɸ) from (1) to (2) Tecplot (V).
Tecplot (θ), Tecplot (ɸ) End. Region 1.
Collocation Method (CM)
Since Trial Function must satisfy the boundary conditions in Eq. (4), so they will be considered as:
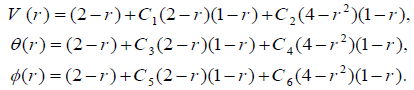 (6)
(6)
We select the collocation locations r=1/3 to 2/3 which are evenly spaced throughout the domain. Introducing these values into the residual Eq. (6). Thus, we have five algebraic equations for the determination of the five unknown coefficients C1 to C6. For example, Using collocation method with (Nb, t=2, C=-1, α=1, M=1, �?=1, Gr=1, Br=1, P=1), V(r), θ(r) and ɸ(r) are as follows:
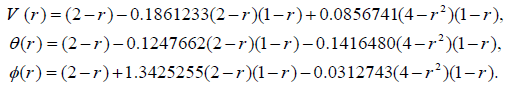 (7)
(7)
Results and Discussion
The comparison of the outcome of Flex-PDE software with the outcome of the CM was done. In addition, this investigation shows that Flex-PDE is strong software to dissolve nonlinear differential equations.
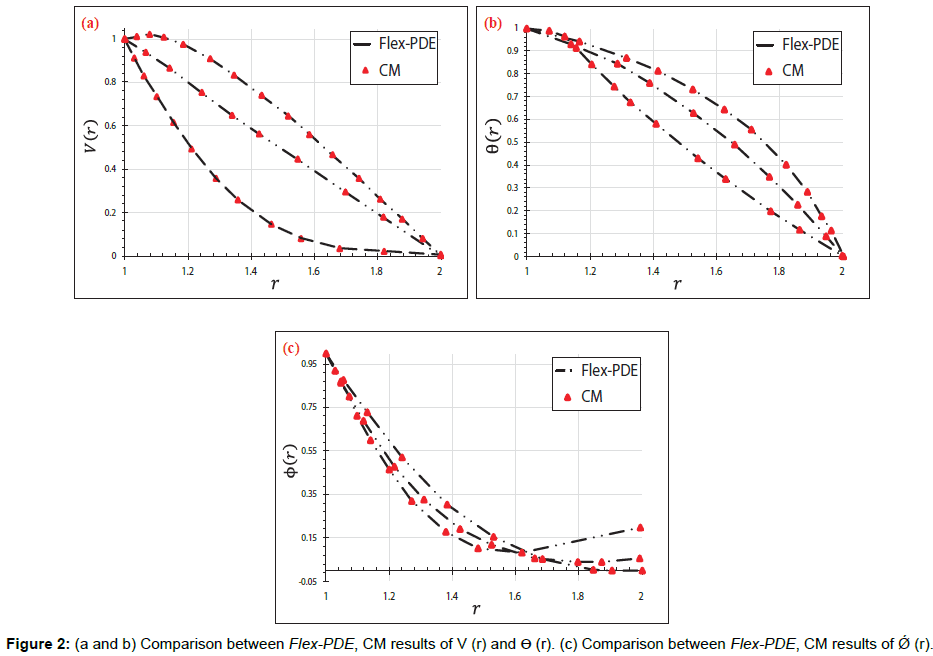
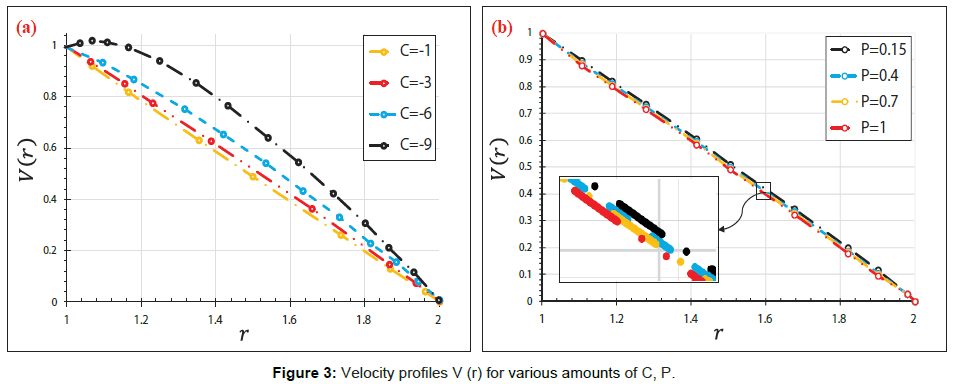
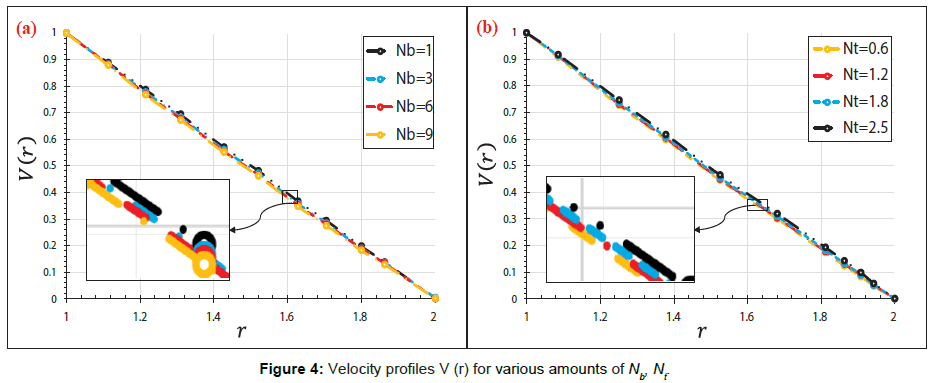
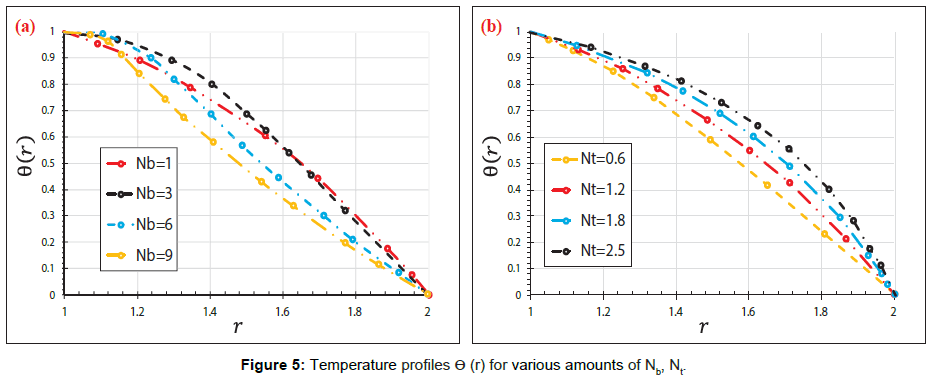
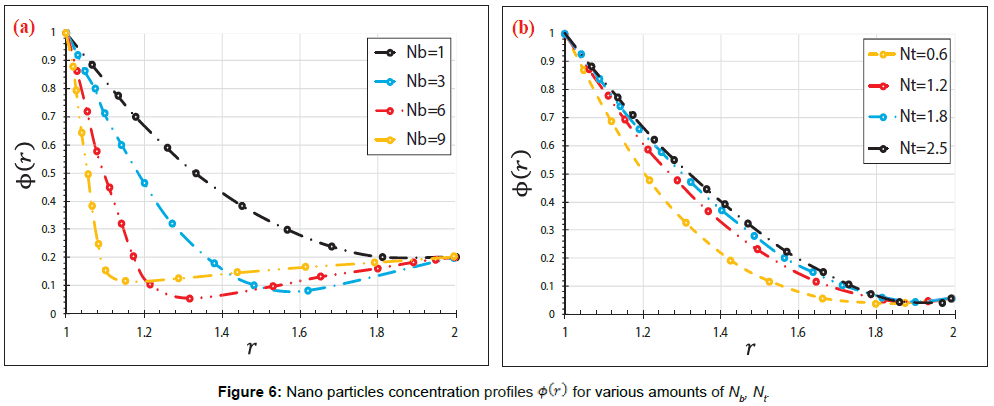
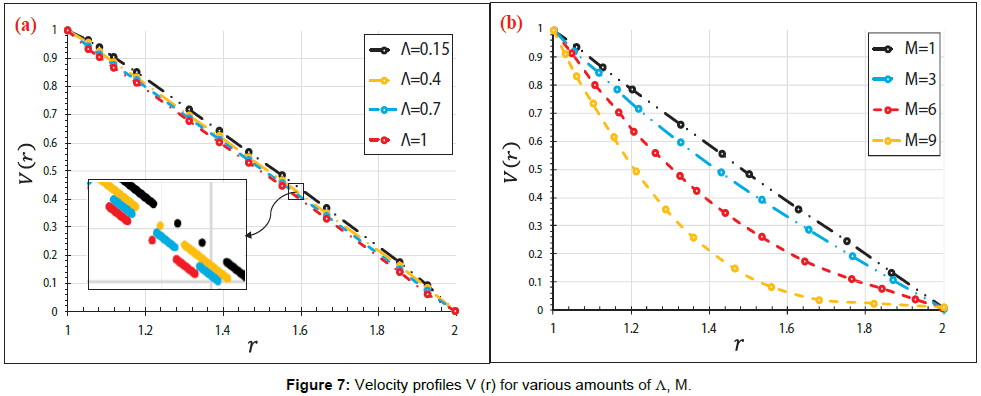
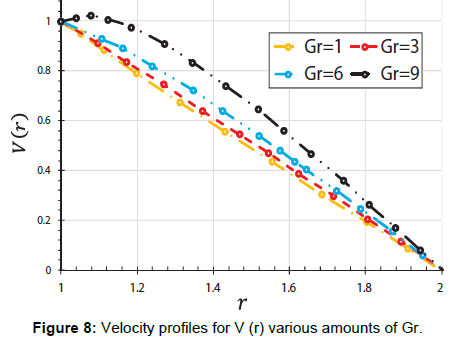
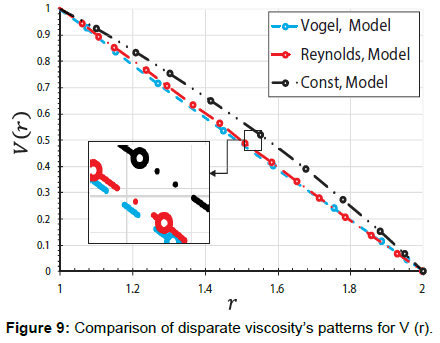
In the present article, the Numerical study on the blood flow with nanoparticles in a magnetic field as a third grade non-Newtonian through porous vessels by using Flex-PDE software to acquire an explicit reply of blood flow with nanoparticles (Figure 1). In order to verify the precision of the present conclusion, we have compared Flex-PDE software outcome with CM method. Comparison between the Flex-PDE software, CM results for various amounts of active parameter are shown in Tables 1-3 and Supplementary Figure A. Also in this perusal, the timings of the solution in order to better assess the present study are shown in Supplementary Figure B. The slight error in Tables 1 and 2; Supplementary Figure B indicates that Flex-PDE is high accuracy software to solve these issues. Figures 2a and 2c represent the comparison between the conclusions of Flex-PDE software, CM method. Due to the observed figures, error is very small between the figures; this means there is complying between the Flex-PDE software, CM method. As well as, in this research the efficacy of various parameters such as the Grashof number, pressure gradient, thermophoresis parameter, Brownian motion parameter and magnetic field intensity on concentration, velocity and temperature profiles are studied. The impact of pressure gradient (C) on velocity profile V (r) is depicted in Figure 3a. The pressure gradient created between the venous end and the arterial of the excursion is the moving force creating blood flow via the vessels, which is negative across the aortal valve throughout the cardiac cycle. Due to the Figure 3a, by decreasing of pressure gradient (C) the amount of velocity profile V(r) increases. Figure 3b shows the impact of different amount of porosity parameter (P) on velocity profile V(r). The velocity repartition is not much affected by variation of various amount of (P), anyway velocity profile slightly increases with Decrease in porosity. Figure 4a and 4b indicates the influence of Brownian motion Parameter Nb and thermophoresis parameter Nt on velocity profile V(r), respectively. Conclusions displays that velocity profile has direct relationship with thermophoresis parameter Nt but Brownian motion Parameter (Nb) has reverse relationship with velocity profile V(r). Figure 5a and 5b depicted the effect of Brownian motion Parameter (Nb) and thermophoresis parameter (Nt) on the temperature profiles ϴ (r) graph, respectively. In Figure 5a, it is clear that Brownian motion parameter does not have a predictable behavior. On the other, it is clear that Brownian motion Parameter (Nb) plays a biotic role in affecting the flow route of platelets or any other cells. Conclusion of Figure 5b illustrate that thermophoresis parameter (Nt) has reverse relationship with temperature profiles. The effect of Brownian motion Parameter (Nb) and thermophoresis parameter (Nt) on the nanoparticles concentration profile ϴ (r) graph, are shown in Figure 6a and 6b, respectively. Conclusion displays that thermophoresis parameter (Nt) has direct relationship with nanoparticles concentration profile ϴ (r) graph, but Brownian motion Parameter (Nb) has reverse relationship with it. This is maybe due to the reality that the effect of thermic conductivity increases by enhancement in (Nb) which leads to the decline in the ϴ (r). Figure 7a and 7b shows the influence of third grade parameter (�?) and MHD parameter (M) on the velocity profile V(r), respectively. According to the Figure 7a, by increasing third grade parameter (�?) velocity profile V(r) decline. However, in Figure 7b, it is observed that the velocity decreases at higher amounts of magnetic field severity. This means, the magnetic field exposure slows down the blood velocity. The impact of Grash of number (Gr) on the velocity profile V(r) graph, are observed in Figure 8. In this Figure, with the increasing Grash of number (Gr), velocity profile V(r) increases. Figure 9 explains the velocity profile V(r) for various Nano fluid viscosity models. It is clear that the highest amounts of velocity are arrived when the Vogel’s model is applied for viscosity of Nano fluid.
| Parts of the Flex-PDE software codes | |
|---|---|
| Title | Definition of title to solve the problem is done in this section |
| Select | User controls that change the default behavior of Flex-PDE |
| Coordinate | It is defining the coordinate system |
| Variables | They are called the dependent variables here |
| Definitions | Parameters, relationships or desired functions are defined in this section |
| Intial values | Determining the initial value of the variables is performed in this section |
| Equations | Each variable is a partial differential equation |
| Constraints | Desired constraints are applied on the problem in this section |
| Extrusion | Extending two-dimensional area in the third dimension in order to build a three-dimensional geometry is performed in this the section |
| Boundaries | Geometry while moving on the boundary domain is created by putting sections of linear or arc together |
| Resolve | Network improvement control command is applied in this section |
| Front | Network improvement control command for issues that are a progressive front is applied in this section |
| Plots | Command of graphic displays the results is applied in this section |
| End | End of the text is determined in this section |
Table 1: Parts of the Flex-PDE software.
| r | Flex– | CM | Error | Flex– | CM | Error |
|---|---|---|---|---|---|---|
| 1 | 1.000000 | 1.000000 | 0.000000 | 1.000000 | 1.000000 | 0.000000 |
| 1.2 | 0.817946 | 0.817831 | 0.000115 | 0.840992 | 0.841852 | -0.000860 |
| 1.4 | 0.436538 | 0.437432 | -0.000894 | 0.571693 | 0.570753 | 0.000940 |
| 1.6 | 0.229196 | 0.227123 | 0.002073 | 0.406767 | 0.405551 | 0.001216 |
| 1.8 | 0.129594 | 0.129071 | 0.000523 | 0.231979 | 0.231121 | 0.000858 |
| 2 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
Table 2: Comparison between the Flex-PDE and CM results for v (left) and θ (Right) at various P, C, Nt, Nb when M=Gr=∧=1.
| r | Flex– | CM | Error |
|---|---|---|---|
| 1 | 0.000000 | 0.000000 | 0.000000 |
| 1.2 | 0.463620 | 0.461451 | 0.002169 |
| 1.4 | 0.987362 | 0.985323 | 0.002039 |
| 1.6 | 0.080756 | 0.081358 | -0.000602 |
| 1.8 | 0.168795 | 0.169280 | -0.000485 |
| 2 | 0.199795 | 0.198857 | 0.000938 |
Table 3: Comparison between the Flex-PDE and CM results for Φ (r) at various P, C, Nt, Nb when Nt=M=Gr=∧=1.
Conclusion
In this essay, the blood flow with nanoparticles in a magnetic field as a third grade non-Newtonian through porous vessels is investigated. For this purpose, new efficient software called Flex-PDE is introduced which solves nonlinear problems. As well as, the impact of various physical parameters like Grashof number, pressure gradient, thermophoresis parameter, Brownian motion parameter and magnetic field intensity on concentration, temperature and velocity profiles are examined. Outcomes displayed that:
• By decreasing of pressure gradient, (C) the amount of velocity profile V(r) increases.
• Result is clear that Brownian motion parameter doesn’t have a predictable behavior.
• The highest amounts of velocity are arrived when the Vogel’s model is applied for viscosity of Nano fluid.
• Conclusions displays that velocity profile has direct relationship with thermophoresis parameter (Nt) but Brownian motion Parameter (Nb) has reverse relationship with velocity profile V(r).
In addition, the performance of the biological systems can be improved by controlling the nanoparticle behavior. This Problem lets helping in the effective transfer of cargo within cells or tissues. Finally, it will be clear that Flex-PDE is excellent analytical software and due to its efficiency, it could be used for solving different issues.
References
- Rashidi MM, Abbasbandy S (2011) Analytic approximate solutions for heat transfer of a micropolar fluid through a porous medium with radiation. Commun Nonlinear Sci Numer Simul 16: 1874-1889.
- Sajid M, Hayat T, Asghar S (2007) Comparison between the HAM and HPM solutions of thin film flows of non-Newtonian fluids on a moving belt. Nonlinear Dyn 50: 27-35.
- Uddin MJ, Yusoff NM, Bég OA, Ismail AM (2013) Lie group analysis and numerical solutions of boundary layer flow of non-Newtonian nanofluids along a horizontal plate in porous medium with internal heat generation. Physica Scripta 87: 025401.
- Bohme G (1987) Non-Newtonian Fluid Mechanics. Elsevier.
- Makinde OD (2007) Thermal stability of a reactive third grade fluid in a cylindrical pipe: an exploitation of Hermite–Padé approximation technique. Appl Math Comput 189: 690-697.
- Loureiro JBR, Freire AS (2013) Asymptotic analysis of turbulent boundary-layer flow of purely viscous non-Newtonian fluids. Journal of Non-Newtonian Fluid Mechanics 199: 20-28.
- Shin S, Ahn HH, Cho YI, Sohn CH (1999) Heat transfer behavior of a temperature-dependent non-Newtonian fluid with Reiner–Rivlin model in a 2: 1 rectangular duct. Int J Heat Mass Transfer 42: 2935-2942.
- Baieth HA (2008) Physical parameters of blood as a non-Newtonian fluid. Int J Biomed Sci 4: 323-329.
- Ogulu A, Amos E (2007) Modeling pulsatile blood flow within a homogeneous porous bed in the presence of a uniform magnetic field and time-dependent suction. Int Comm Heat Mass Trans 34: 989-995.
- Nandakumar N, Sahu KC, Anand M (2015) Pulsatile flow of a shear-thinning model for blood through a two-dimensional stenosed channel. European Journal of Mechanics-B/Fluid 49: 29-35.
- Moyers-Gonzalez MA, Owens RG, Fang J (2008) A non-homogeneous constitutive model for human blood: Part III. Oscillatory flow. Journal of Non-Newtonian Fluid Mechanics 155: 161-173.
- Srinivas S, Vijayalakshmi A, Reddy AS (2016) Flow and Heat Transfer of Gold-Blood Nanofluid in a Porous Channel with Moving/Stationary Walls. J Mech 1-10.
- Sinha A, Shit GC, Kundu PK (2013) Slip effects on pulsatile flow of blood through a stenosed arterial segment under periodic body acceleration. ISRN Biomed Eng 2013: 1-10.
- Aziz A, Aziz T (2012) MHD flow of a third grade fluid in a porous half space with plate suction or injection: an analytical approach. Appl Math Comput 218: 10443-10453.
- Hatami M, Hatami J, Ganji DD (2014) Computer simulation of MHD blood conveying gold nanoparticles as a third grade non-Newtonian nanofluid in a hollow porous vessel. Comput Methods and Programs Biomed 113: 632-641.
- Baoku IG, Olajuwon BI, Mustapha AO (2013) Heat and mass transfer on a MHD third grade fluid with partial slip flow past an infinite vertical insulated porous plate in a porous medium. Int J Heat Fluid Flow 40: 81-88.
- Mekheimer KS, Haroun MH, El Kot MA (2012) Influence of heat and chemical reactions on blood flow through an anisotropically tapered elastic arteries with overlapping stenosis. Appl Math 6: 281-292.
- Reasor DA, Clausen JR, Aidun CK (2012) Coupling the lattice�?�Boltzmann and spectrin�?�link methods for the direct numerical simulation of cellular blood flow. Int J Num Methods Fluid 68: 767-781.
- Hatami M, Ganji DD (2013) Heat transfer and flow analysis for SA-TiO2 non-Newtonian nanofluid passing through the porous media between two coaxial cylinders. J Mol Liq 188: 155-161.
- Rahbari A, Fakour M, Hamzehnezhad A, Vakilabadi MA, Ganji DD (2017) Heat transfer and fluid flow of blood with nanoparticles through porous vessels in a magnetic field: A quasi-one dimensional analytical approach. Math Biosci 283: 38-47.
- Akbari N, Ganji DD, Gholinia M, Gholinia S (2016) Analytical and Numerical Study to Nonlinear Heat Transfer Equation in Strait Fin. Innov Ener Res 5: 148.
- Gholinia M, Ganji DD, Poorfallah M, Gholinia S (2016) Analytical and Numerical Method in the Free Convection Flow of Pure Water NonNewtonian Nano fluid between Two Parallel Perpendicular Flat Plates. Innov Ener Res 5: 142.
- Ozisik MN (1993) Heat conduction. John Wiley & Sons, USA.
Relevant Topics
- Advanced Photovoiltoic Cells
- Advanced Photovoiltoic Panels
- Advanced Photovoiltoic Systems
- Advanced Photovoiltoic Technologies
- Alternative Energy
- Biomass Energy
- Coal Energy
- Energy Management
- Environmental Policy
- Green Energy
- Hydro Electric Energy
- Hydrogen Energy
- Hydropower Energy
- Photovoltoics
- Renewable Energy and Research
- Renewable Geothermal Energy
Recommended Journals
Article Tools
Article Usage
- Total views: 4229
- [From(publication date):
June-2017 - Aug 18, 2025] - Breakdown by view type
- HTML page views : 3204
- PDF downloads : 1025