Convective Ramped Wall Temperature and Concentration Boundary Layer Flow of a Chemically Reactive Heat Absorbing and Radiating Fluid over a Vertical Plate in Conducting Field with Hall Current
Received: 11-Jan-2016 / Accepted Date: 12-Feb-2016 / Published Date: 19-Feb-2016
Abstract
An exact solution for an unsteady MHD free convection flow of a viscous incompressible, electrically conducting, optically thick radiating and heat absorbing fluid past an accelerated moving vertical plate with variable ramped wall temperature and as well as ramped wall concentration in the presence of Hall current is investigated. The dimensionless governing equations are solved in the closed form using Laplace transform technique. The expressions for the fluid velocity, fluid concentration and fluid temperature are obtained. The effects of various physical parameters on fluid velocities, fluid temperature and fluid concentration are displayed graphically where as those of shear stress and rate of heat transfer at the plate are presented in the tabular form.
Keywords: MHD; Hall effect; Radiation; Heat absorption; Ramped wall temperature; Ramped wall concentration
18533Introduction
Effect of thermal radiation on hydro magnetic free convection flow plays an important role in several scientific and industrial processes such as high temperature casting and levitation, thermo-nuclear fusion, furnace design, glass production, solar power technology, etc. Chandrakala [1] analyzed radiation effects on flow past an impulsively started vertical oscillating plate with uniform heat flux. Chandram et al. [2] investigated natural convection near a vertical plate with ramped wall temperature. Prasad and Reddy [3] observed radiation effects on an unsteady MHD convective heat and mass transfer flow past a semi-infinite vertical permeable moving plate embedded in a porous medium. Chandrakala and Bhaskar [4] considered thermal radiation effects on MHD flow past a vertical oscillating plate. Israel-Cookey et al. [5] examined MHD oscillatory couette flow of a radiating viscous fluid in a porous medium with periodic wall temperature. Jain and Singh [6] noticed that Hall and thermal radiation effects on an unsteady rotating free convection slip flow along a porous vertical moving plate. Aurangzaib and Sharidan [7] obtained effects of Soret and Dufour on unsteady MHD flow by mixed convection over a vertical surface in porous media with internal heat generation, chemical reaction and Hall current. Chaudhary et al. [8] presented effects of Hall current and thermal radiation on an unsteady free convection slip flow along a vertical plate embedded in a porous medium with constant heat and mass flux. Shateyi et al. [9] analyzed the effects of thermal radiation, Hall currents, Soret and Dufour on MHD flow by mixed convection over a vertical surface in porous media. Seth et al. [10] discussed effects of thermal radiation and rotation on unsteady hydromagnetic free convection flow past an impulsively moving vertical plate with ramped temperature in a porous medium. Shit and Haldar [11] have investigated combined effects of thermal radiation and Hall current on MHD free-convective flow and mass transfer over a stretching sheet with variable viscosity. Singh and Pathak [12] studied effect of rotation and Hall current on mixed convection MHD flow through a porous medium in a vertical channel in presence of thermal radiation. Takhar and Ram [13] assumed free convection in hydromagnetic flows of a viscous heat-generating fluid with wall temperature oscillation and Hall currents. Ahmed and Sharma [14] have considered the radiation effect on a transient MHD flow with mass transfer past an impulsively fixed infinite vertical plate. Rajesh and Varma [15] solved radiation effects on MHD flow through a porous medium with variable temperature or variable mass diffusion. Vijayalakshmi and Kamalam [16] established effects of radiation on an accelerated vertical plate with uniform mass diffusion. Ahmad et al. [17] examined unsteady MHD free convective flow past a vertical porous plate immersed in a porous medium with Hall current, thermal diffusion and heat transfer. Ahmed and Sarmah [18] MHD transient flow past an impulsively started horizontal porous plate in a rotating system with Hall current. Seth et al. [19] obtained effect of rotation on unsteady hydromagnetic natural convection flow past an impulsively moving vertical plate with ramped temperature in a porous medium with thermal diffusion and heat absorption. Malique and Sattar [20] presented the effects of variable properties and Hall current on steady MHD laminar convective fluid flow due to a porous rotating disk. Seth and Ansari [21] analyzed MHD natural convection flow past an impulsively moving vertical plate with ramped wall temperature in the presence of thermal diffusion with heat absorption. Seth et al. [22] discussed hartmann flow in a rotating system in the presence of inclined magnetic field with Hall effects. Kumar et al. [23] has investigated hydromagnetic couette flow in a rotating system with Hall effects. Seth et al. [24] studied Hall effects on oscillatory hydromagnetic couette flow in a rotating system. Kinyanjui et al. [25] assumed magneto hydrodynamic free convection heat and mass transfer of a heat generating fluid past an impulsively started infinite vertical porous plate with Hall current and radiation absorption. Cookey et al. [26] have considered influence of viscous dissipation and radiation on unsteady MHD free convection flow past an infinite heated vertical plate in a porous medium with time dependent suction. Aboeldahab and Aziz [27] solved viscous dissipation and Joule heating effects on MHD free convection from a vertical plate with power-law variation in surface temperature in the presence of Hall and ion-slip currents. Seth et al. [28] established effect of rotation on heat transfer characteristics of hydromagnetic channel flow in the presence of inclined magnetic field. Seth [29] examined effects of Hall current on unsteady hydro magnetic couette flow in a rotating system. Muthucumaraswamy and Ganesan [30] obtained radiation effects on the flow past an impulsively started infinite vertical plate with variable temperature. Seth et al. [31] presented effect of hall current on hydromagnetic free and forced convection flow in a rotating channel. Seddeek et al. [32] analyzed radiation effects on unsteady MHD free convection with hall current near an infinite vertical porous plate. Aboedahab and Elbarbary [33] have investigated hall current effect on magneto hydrodynamic free-convection flow past a semi-infinite vertical plate with mass transfer. Kumar et al. [34] studied effect of inclination of applied magnetic field and hall current on generalized oscillatory MHD Couette flow. Das et al. [35] has considered unsteady hydromagnetic flow of a heat absorbing dusty fluid past a permeable vertical plate with ramped temperature. Thermal and solutal buoyancy effect [36,37] on MHD boundary layer flow of a visco-elastic fluid past a porous plate with varying suction and heat source in the presence of thermal diffusion was investigated by Chandra et al. [38] recently. Unsteady MHD free convection flow of a viscous dissipative Kuvshinski fluid past an infinite vertical porous plate in the presence of radiation, thermal diffusion and chemical effects were considered by Vidyasagar et al. [39]. Heat and mass transfer in MHD mixed convection flow on a moving inclined porous plate was investigated by Raju et al. [40].
The aim of the present study is to investigate an unsteady MHD free convection flow of a viscous incompressible, electrically conducting, optically thick radiating and heat absorbing fluid past an accelerated moving vertical plate with variable ramped wall temperature and as well as ramped wall concentration in the presence of Hall current.
Formulation Of The Problem And Its Solution
Consider unsteady hydro magnetic free convection flow of a viscous, incompressible, electrically conducting, optically thick radiating and heat absorbing fluid past a moving infinite vertical plate with variable ramped temperature. We choose the Cartesian coordinate system (x1, y1, z1) in such a way that x1-axis is along the vertical plate upward direction, y1-axis is normal to x1y1-plane. A uniform transverse magnetic field of strength B0is applied in a direction parallel to y1-axis. Initially, i.e., at time t1 < 0, both the plate and surrounding fluid are at rest and maintained at uniform temperatureT∞1. At time t1 > 0, the plate starts moving along x1direction with a velocity U(t1) = a1t1 (a1 being arbitrary constant) and at the same time temperature of the plate is raised to 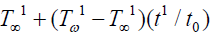 when
when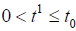 and it is maintained at uniform temperature
and it is maintained at uniform temperature 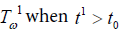 (t0 being critical time for rampedness).
(t0 being critical time for rampedness).
Since plate is of infinite extent along x1 and z1directions, all physical quantities except pressure depend on y1 and t1 only. Induced magnetic field produced by fluid motion in neglected in comparison to applied one. This is justified because magnetic Reynolds number is very small for liquid metals and partially ionized fluids, which are commonly used in various industrial processes. Since no external electric field is applied into the flow-field so the effect of polarization of fluid is negligible which corresponds to the case where no energy is added or extracted from the fluid by electrical means.
With the assumptions made above, the governing equations for the fluid flow problem considering Hall current, under Boussinesq approximation, are given by
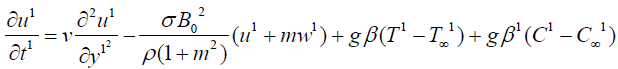 (1)
(1)
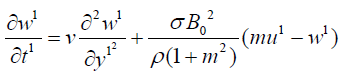 (2)
(2)
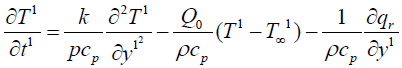 (3)
(3)
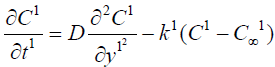 (4)
(4)
Initial and boundary conditions to be satisfied are
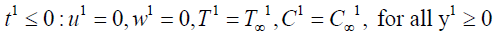 (5)
(5)
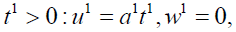
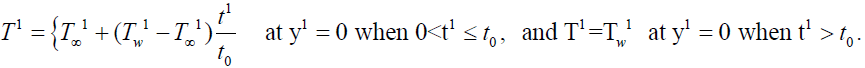 (6)
(6)
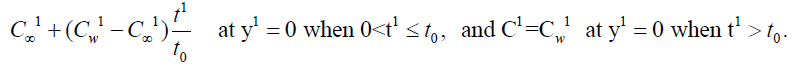
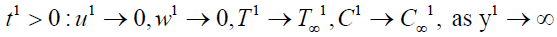 (7)
(7)
For an optically thick gray fluid, the radiative heat flux qr is approximated by Ross eland approximation that is given
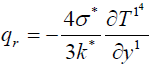 (8)
(8)
It is assumed that the temperature difference between fluid in the boundary layer region and free-stream is very small so that t14 may be expressed as a linear function of temperatureT1. Expanding t14 in Taylor series about T∞1 and neglecting second and higher order terms, we get
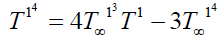 (9)
(9)
Using equations (9) and (8) in (3) we get
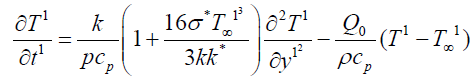 (10)
(10)
We introduce following non dimensional quantities and flow parameters to present (1), (2) and (10) along with initial and boundary conditions (5)-(7) in non-dimensional form
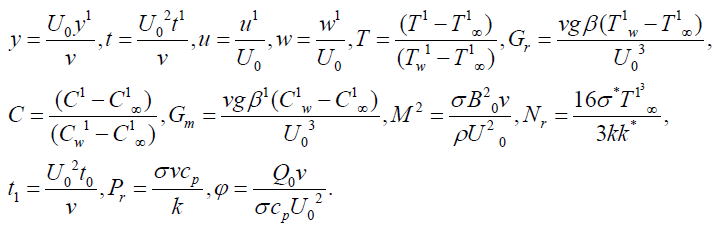 (11)
(11)
Making use of equation (11), equations (1), (2), (4) and (10), in non-dimensional form, reduce to
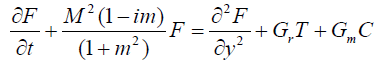 (12)
(12)
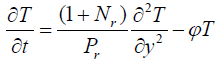 (13)
(13)
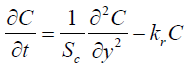 (14)
(14)
Where F( y,t) = u( y,t) + iw( y,t).
Initial and boundary conditions (5) to (7), in non-dimensional form, are given by
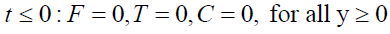 (15)
(15)
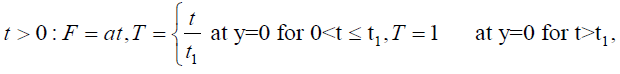 (16)
(16)
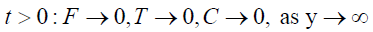 (17)
(17)
Where 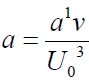 is non-dimensional constant
is non-dimensional constant
It is evident from equation (12), (13) and (14) that energy equation (13) is uncoupled from momentum equation (13). Using Laplace transform technique, first the solution for fluid temperature T (y,t) is obtained by solving equation (13) and second the solution fluid concentrate C (y,t) is obtained by solving equation (14) subject to the initial and boundary conditions (15) to (17) and then using this solution in equation (12), solution for fluid velocity F (y,t) is obtained. The exact solutions for fluid temperature T (y, t), the exact solutions for fluid concentrate C (y,t) and fluid velocity F (y,t) are obtained and expressed in the following simplified form (equations 18, 19 and 20 are solutions).
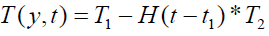 (18)
(18)
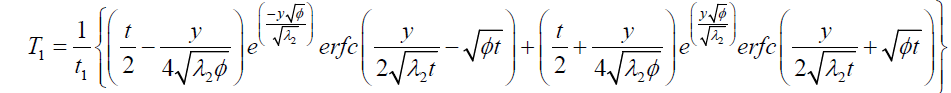
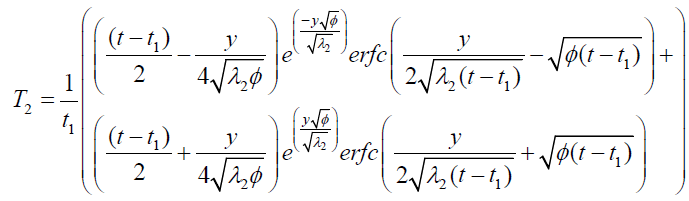
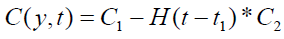 (19)
(19)
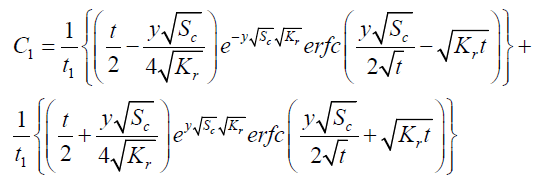
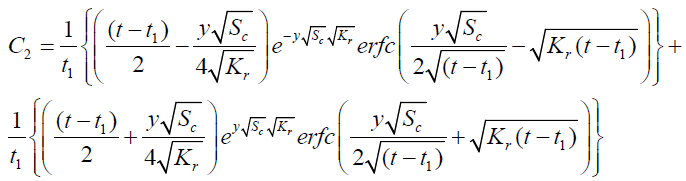
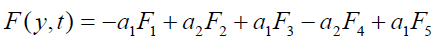 (20)
(20)
where
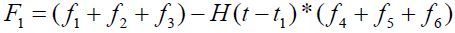
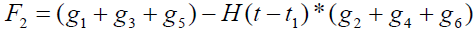
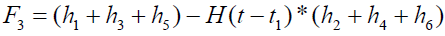
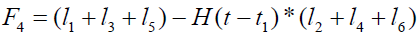
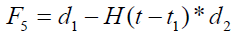
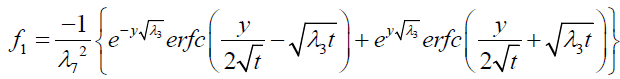
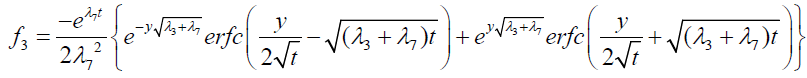
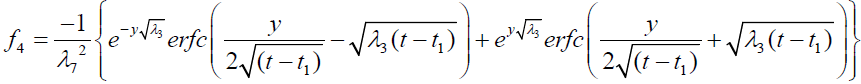
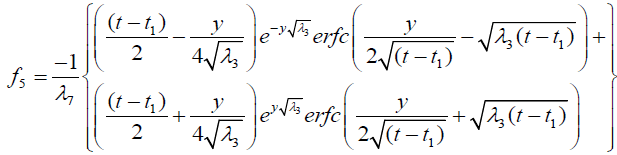
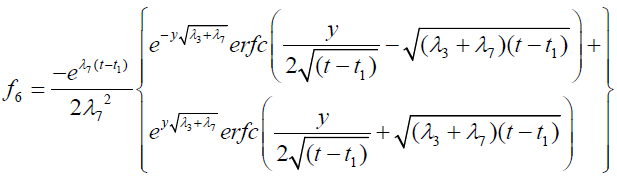
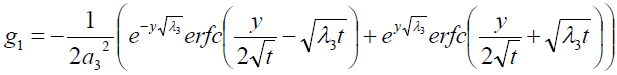
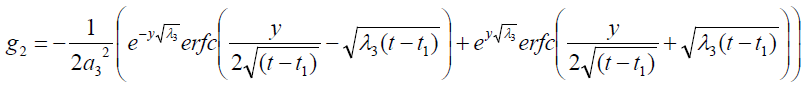
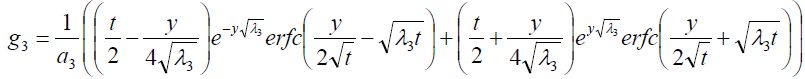
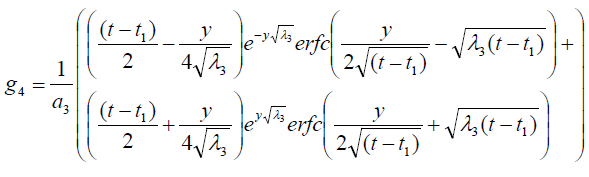
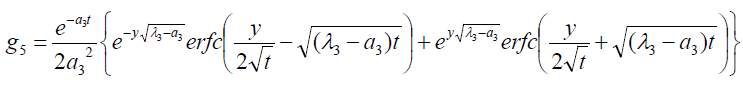
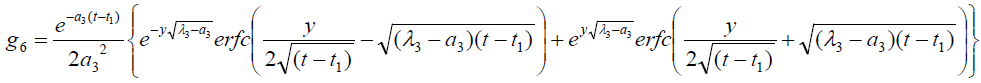
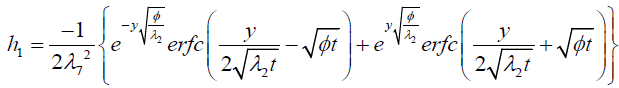
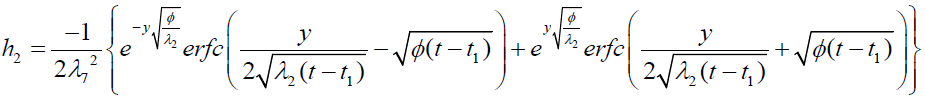
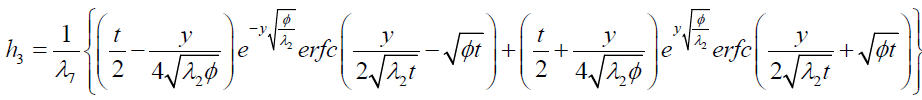
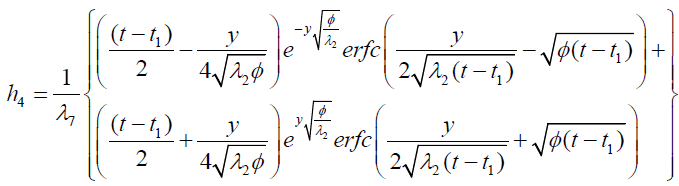
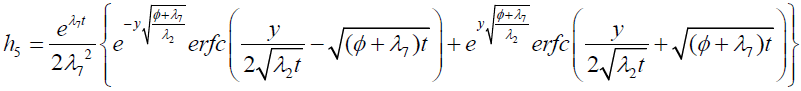
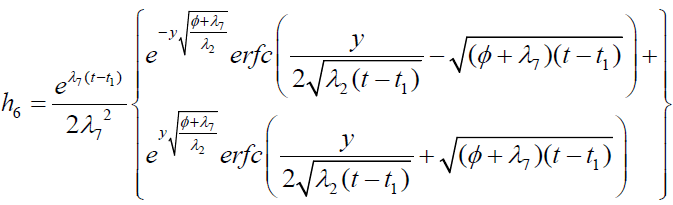
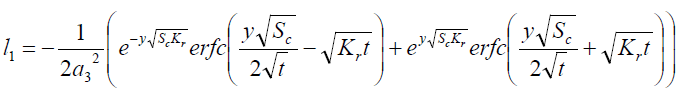
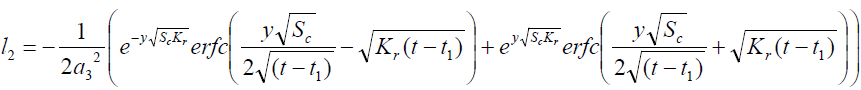
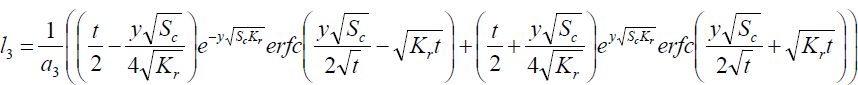
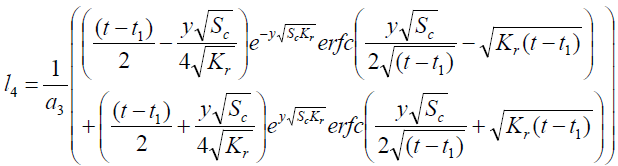
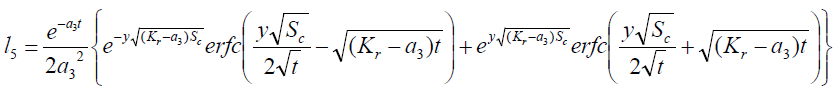
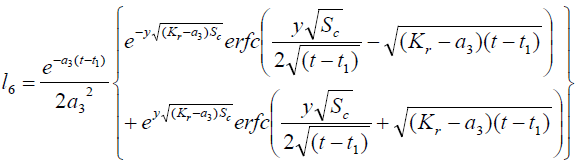
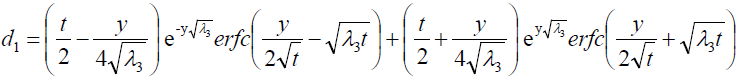
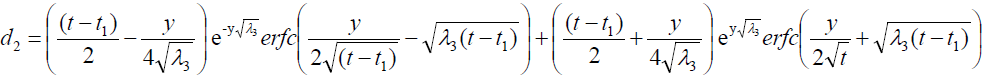
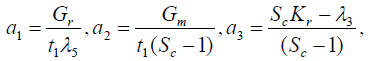
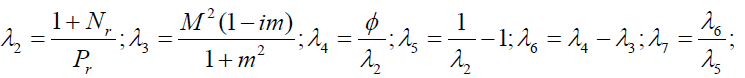
Expression for rate of heat transfer at the plate, i.e., the rate of heat transfer in terms of Nusselt number is given by
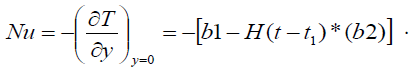 (21)
(21)
Another important physical quantity is the mass transfer coefficient, i.e., the Sherwood number, which is in non-dimensional form, is given by
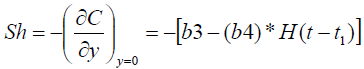 (22)
(22)
The skin friction at the plate in non-dimensional form is given by
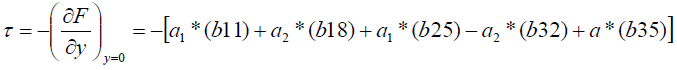 (23)
(23)
Where
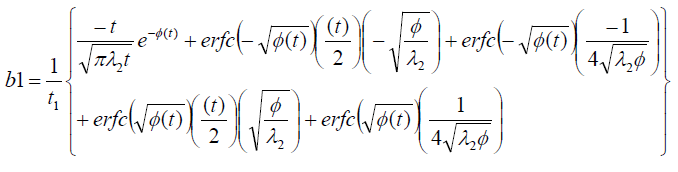
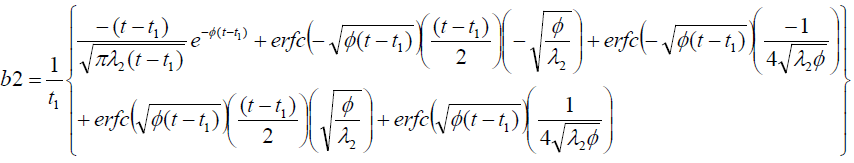
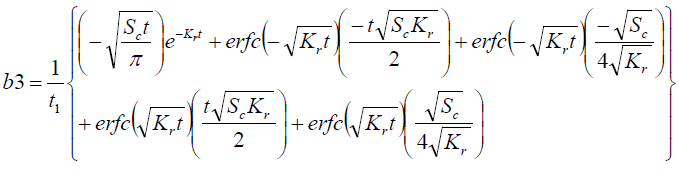
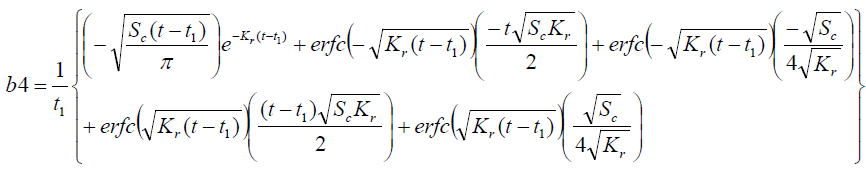
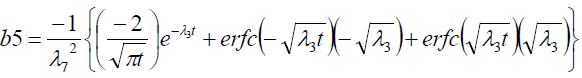
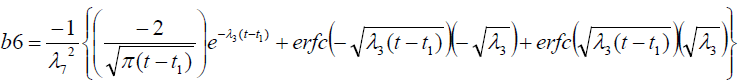
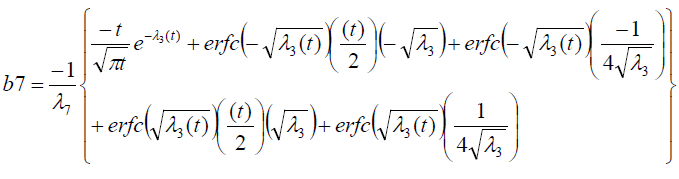
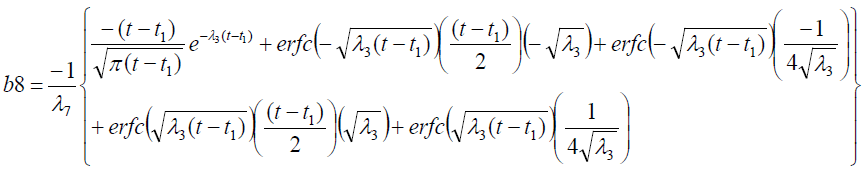
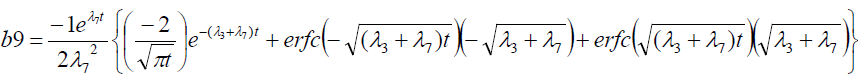
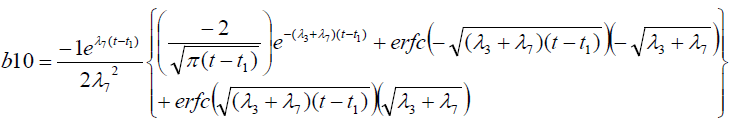
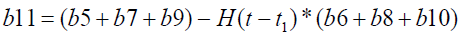
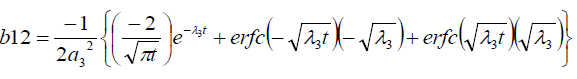
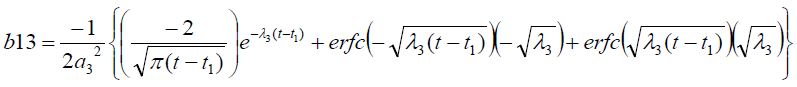
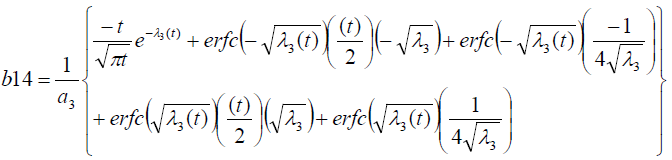
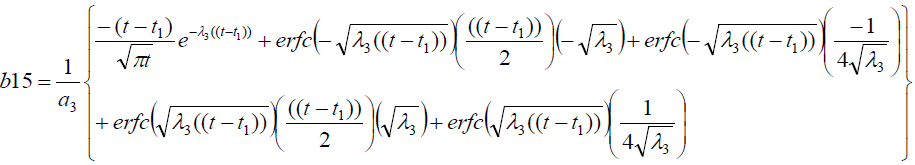

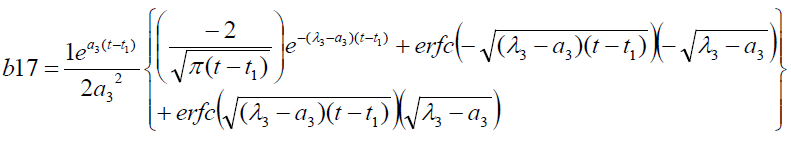
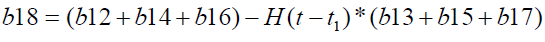
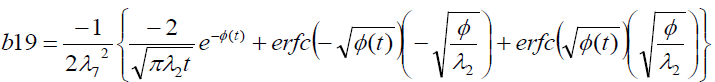
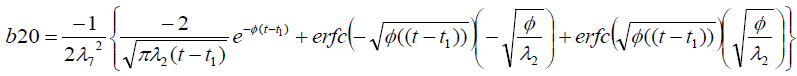
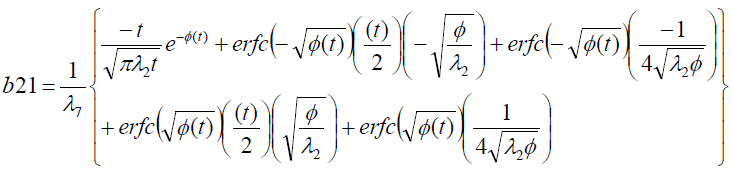
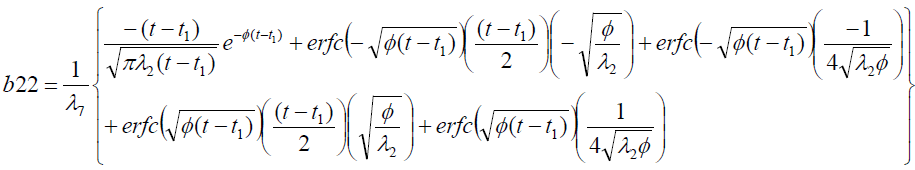
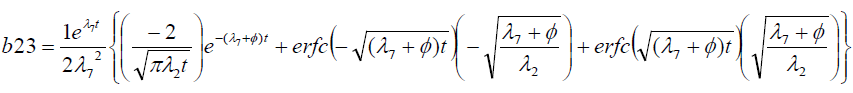
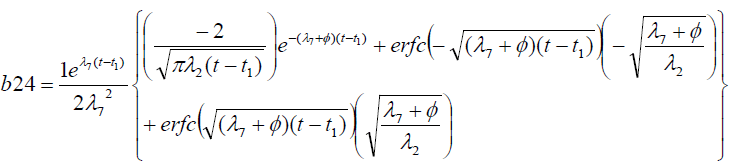
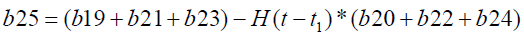
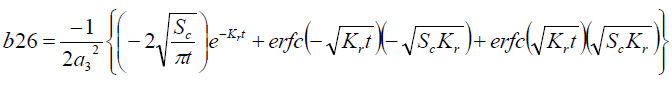
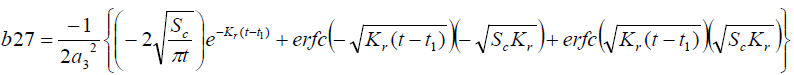
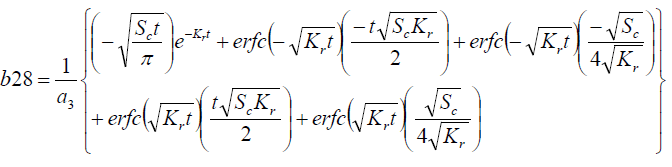
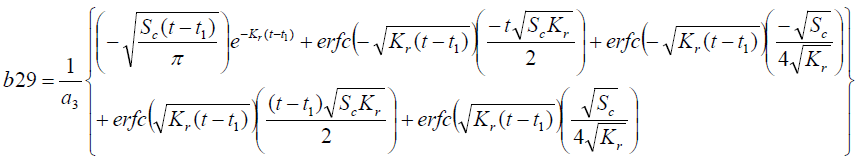
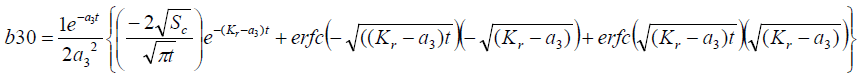
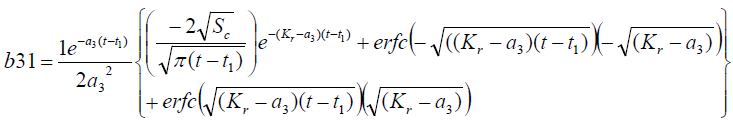
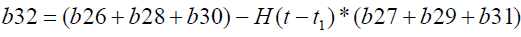
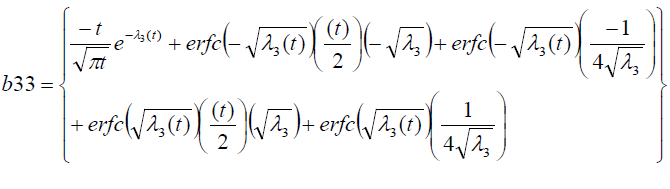
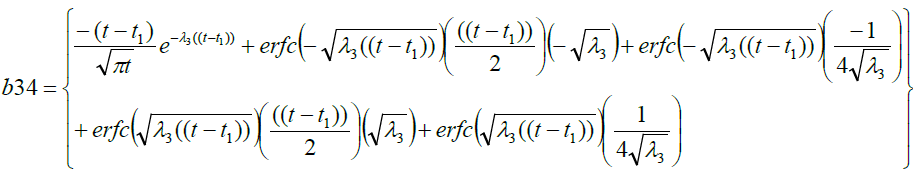
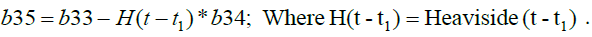
Results And Discussion
To gain a perspective of the physics of the flow regime, we have studied numerically the effects of Magnetic field (M), Grashoff number (Gr), modified Grashof number (Gm), Prandtl number (Pr), heat absorption parameter (Q orφ ), radiation parameter (Nr), Schmidt number (Sc), chemical reaction parameter (Kr), Hall current (m1) and various values of critical time for rampedness (t1) on the velocity, temperature, concentration, shear stress function, Nusselt number and Sherwood number.
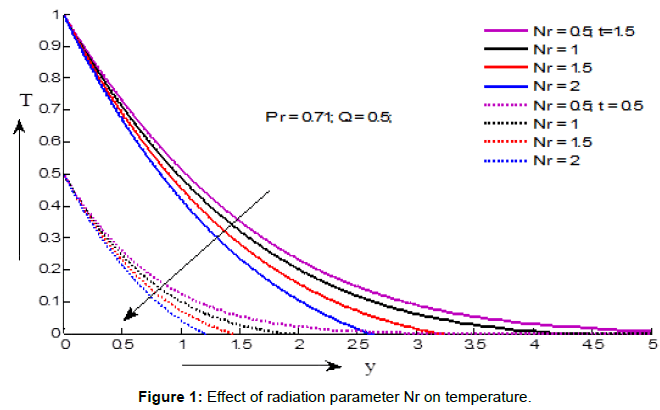
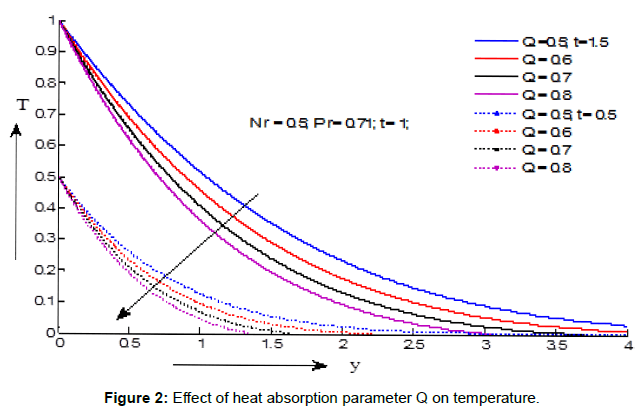
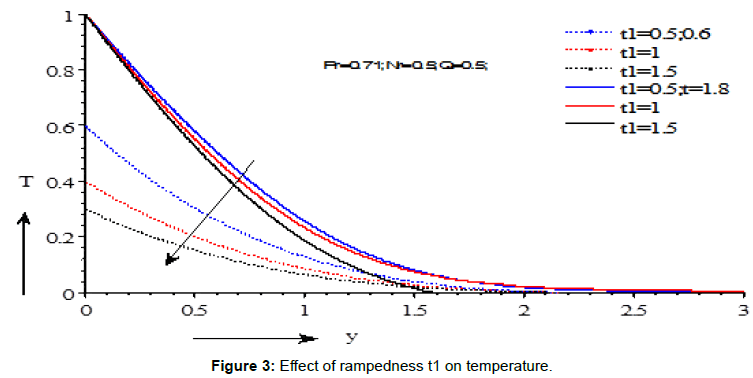
Figures 1-3 demonstrate the variations of the fluid temperature under the effects of different parameters. The effects of radiation parameter on temperature are presented in Figure 1 and it is seen that the surface temperature decreases with the increasing values of radiation parameter for both the cases of t = 1.8 and t = 0.6. The effect of heat absorption parameter on temperature is exhibited in Figure 2. It shows that the temperature decreases with the increasing values of heat absorption parameter for the values of t=1.5 and t=0.5. The effects of critical time for rampedness on temperature are exhibited in Figure 3. It is observed that the temperature decreases with the increasing values of critical time for rampedness for the values of t=1.8 and t=0.6.
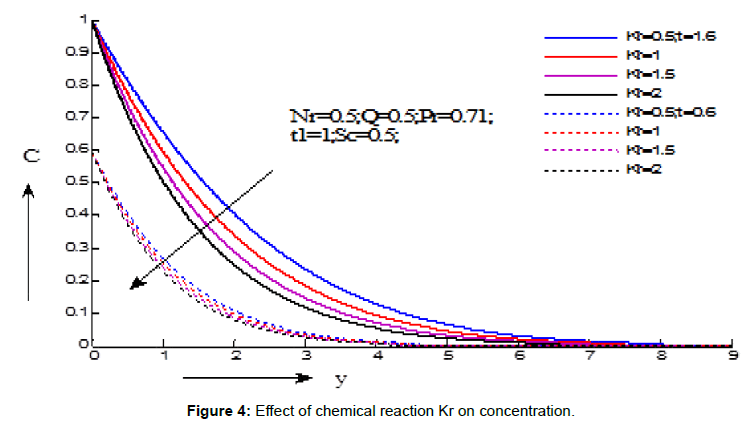
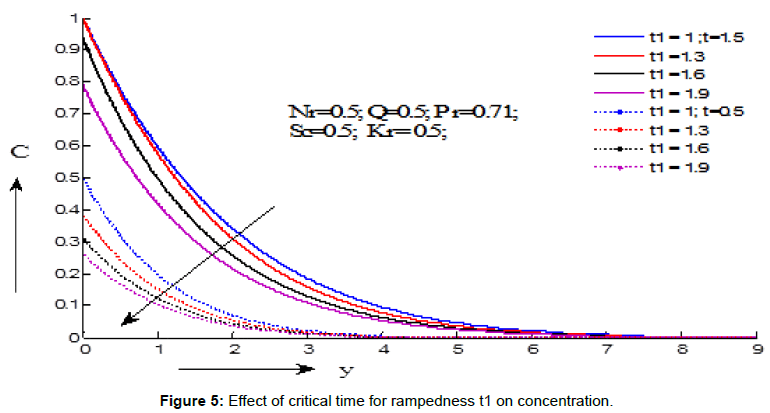
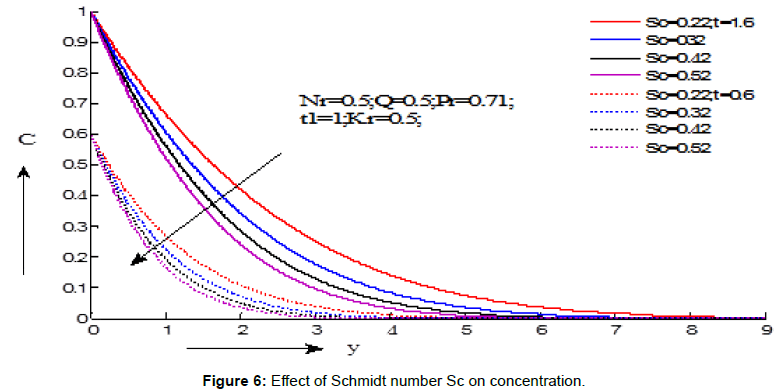
Figures 4-6 indicates the variations of the fluid concentration under the efects of different parameters. Figure 4 illustrates the influence of chemical reaction on the concentration. It is noticed that concentration decreases with the increasing values of chemical reaction for the values of t=1.6 and t=0.6. Figure 5 exhibits the influence of critical time for rampedness on the concentration. It is seen that concentration decreases with the increasing values of critical time for rampedness for the values of t=1.5 and t=0.5. Figure 6 presents the influence of Schmidt number on the concentration. It is perceived that concentration decreases with the increasing values of Schmidt number for the values of t=1.6 and t=0.6.
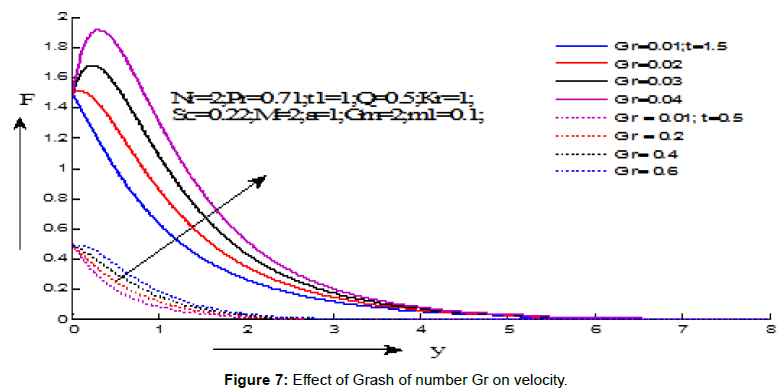
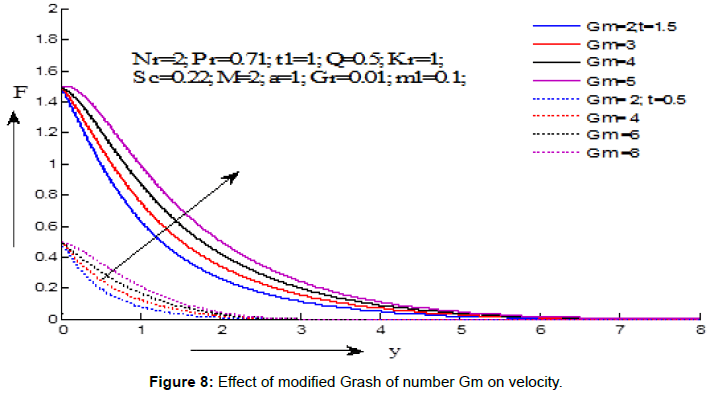
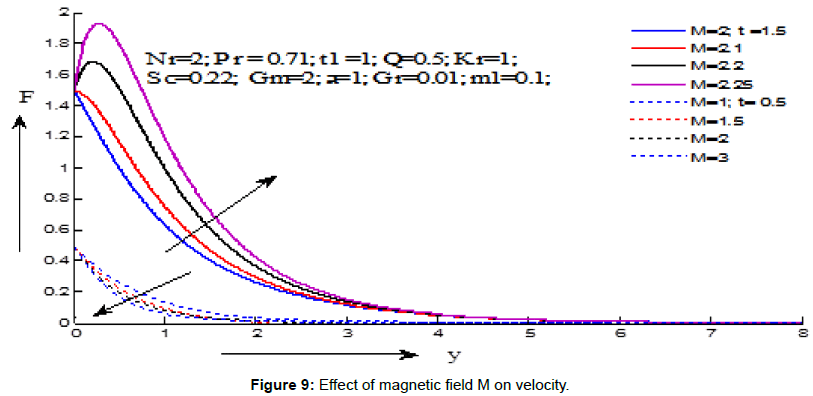
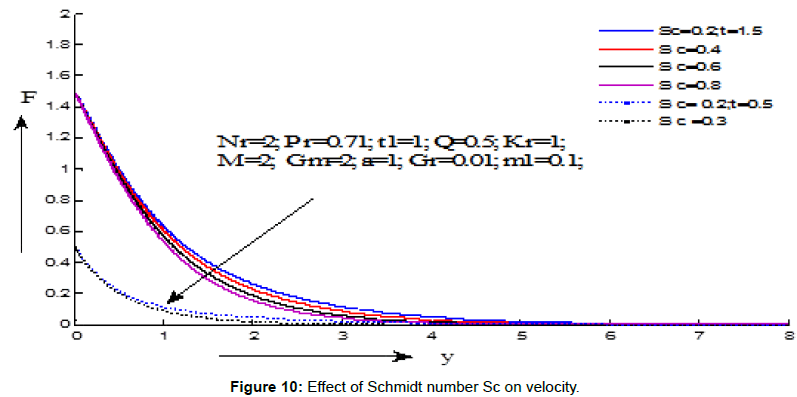
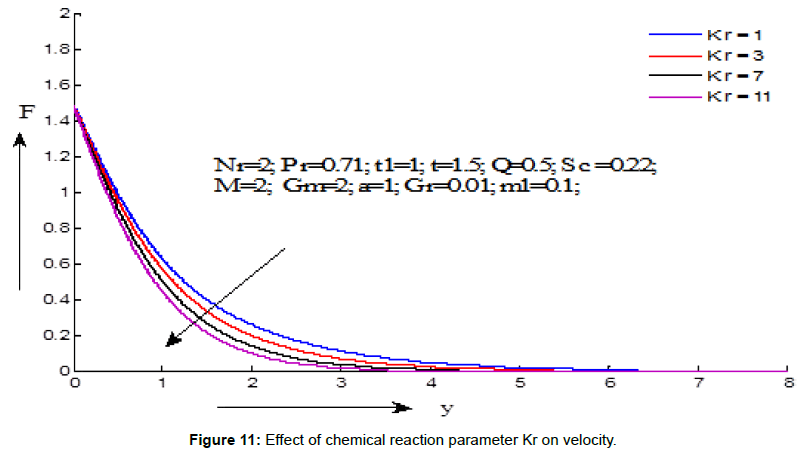
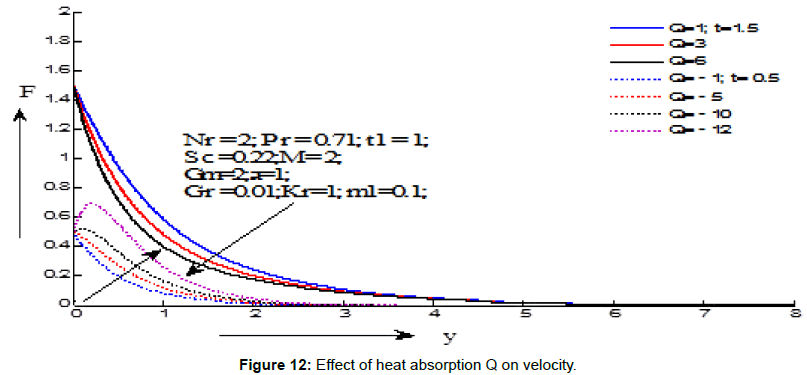
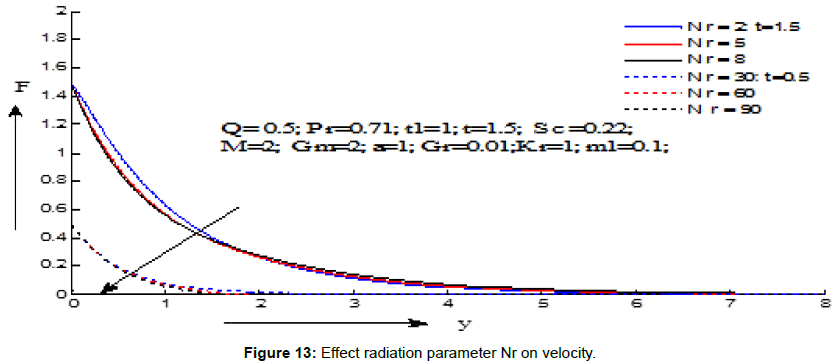
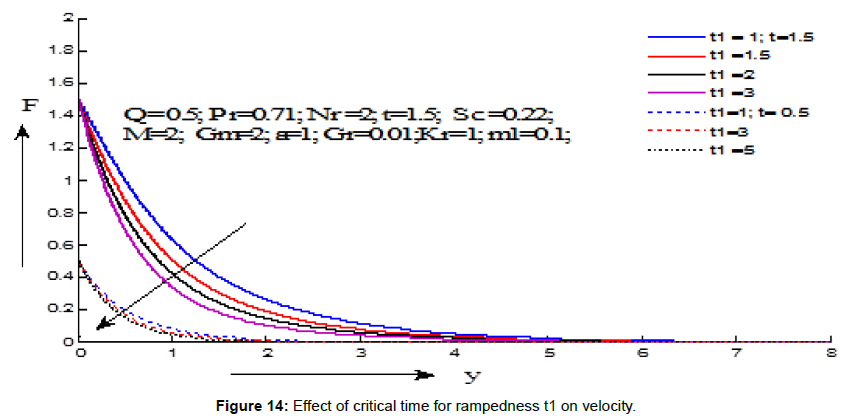
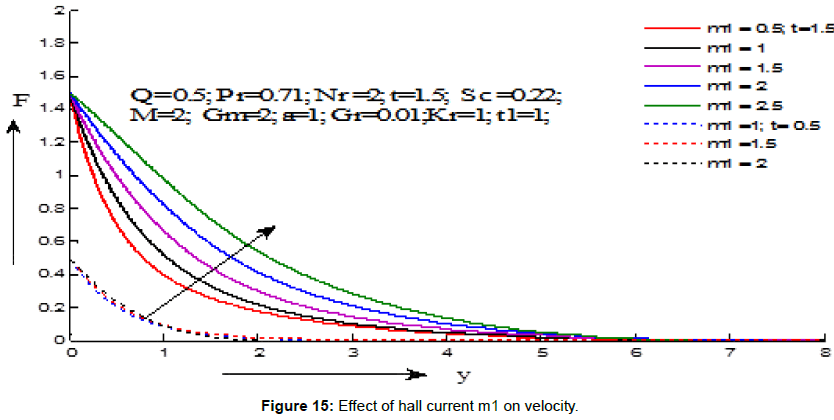
Figures 7-15 demonstrate the variations of the fluid velocity under the effects of different parameters. Figure 7 shows the effect of Grashf numer on velocity distribution. It is noticed that the velocity increases with the increasing values of Grashf number for the values of t=1.5 and t=0.5. Figure 8 depicts the effect modified Grashf numer on velocity distribution. It is shows that the velocity increases with the increasing values of modified Grashf number for the values of t=1.5 and t=0.5. Figure 9 exhibites the effect of Magnetic field on velocity distribution. It is observed that the velocity increases with the increasing values of Magnetic field number for the value of t=1.5 but decreses for the value of t=0.5. Figure 10 displays the effect of Schmidt number on velocity distribution. It is noticed that the velocity decreases with the increasing values of Schmidt number for the values of t=1.5 and t=0.5. Figure 11 demonstrates the effect of chemical reaction on velocity distribution. It is seen that the velocity decreases with the increasing values of chemical reaction parameter for the values of t=1.5 and t=0.5. Figure 12 displays the effect heat absorption on velocity distribution. It can be seen that the velocity decreases with increasing the values of heat absorption parameter for the value of t=1.5 but velocity increses with decreasing values (negative values) of heat absorption parameter for the value of t=0.5. Figure 13 presents the effect of radiation parameter on velocity distribution. It is perceived that the velocity decreases with the increasing values of radiation parameter for the values of t=1.5 and t=0.5. Figure 14 depicts the effect of critical time for rampedness on velocity distribution. It is shows that the velocity decreases with the increasing values of critical time for rampedness for the values of t=1.5 and t=0.5. Figure 15 depicts the effect of Hall current on velocity distribution. It is noticed that the velocity increases with the increasing values of Hall current for the values of t=1.5 and t=0.5.
We also recorded numerical values of the surface skin friction (τ), Nusselt number (Nu) and Sherwood number (Sh) in tabular form. From Table 1 it is observed that Nusselt number and skin fraction decreases for increasing values of Nr. From Table 2 it is noticed that Nusselt number decreases for the increasing values of Nr. whereas skin friction increases for increasing values of Nr. From Table 3 it is noted that Nusselt number increase due to an increase in heat absorption parameter Q orφ and skin friction decrease due to an increase in heat absorption parameter. From Table 4 it is cleared that both Nusselt number and skin friction increase due to an increase in heat absorption parameter. From Table 5 it is shows that both Nusselt number and skin friction decrease due to an increase in rampedness t1. From Table 6 it is noticed that Nusselt number decrease due to an increase in rampedness and skin friction increase due to an increase in rampedness. From Table 7 it is observed that Sherwood number increase due to an increase in reaction parameter Kr (but reverse skin friction) and skin friction increase due to a decrease in chemical reaction. From Table 8 it is cleared that both Sherwood number and skin friction increase due to an increase in chemical reaction parameter. From Table 9 it is noted that Sherwood number increase due to an increase in Schmidt number (but reverse skin friction) and skin friction increase due to a decrease in Schmidt number. From Table 10 it is shows that both Sherwood number and skin friction increase due to an increase in Schmidt number. From Table 11 it is observed that skin friction increase due to an increase in Grashof number. From Table 12 it is show that skin friction decrease due to an increase in Grashof number. From Table 13 it is noticed that skin friction decrease due to an increase in modified Grashof number. From Table 14 it is cleared that skin friction increase due to an increase in modified Grashof number. From Table 15 it is examined that skin friction decrease due to an increase in Hall current (m1). From Table 16 it is noticed that skin friction increase due to an increase in Hall current (m1). From Tables 17 and 18 it is observed that skin friction decrease due to an increase in Magnetic field.
| Nr at t=1.5 | Nu | Sh | τ |
| 0.5 | 0.6939 | 0.4986 | 12.9691 |
| 1 | 0.6009 | 0.4986 | 4.1934 |
| 1.5 | 0.5375 | 0.4986 | 2.7115 |
| 2 | 0.4906 | 0.4986 | 2.1841 |
Table 1: Variations in skin friction, Nusselt number and Sherwood number with Nr and t.
| Nr at t=0.5 | Nu | Sh | τ |
| 0.5 | 0.8073 | 0.4337 | 0.1530 |
| 1 | 0.6992 | 0.4337 | 0.1569 |
| 1.5 | 0.6254 | 0.4337 | 0.1579 |
| 2 | 0.5709 | 0.4337 | 0.1582 |
Table 2: Variations in skin friction, Nusselt number and Sherwood number with Nr and t.
| Q (=Φ) at t=1.5 | Nu | Sh | τ |
| 0.5 | 0.6939 | 0.4986 | 12.9691 |
| 1 | 0.9308 | 0.4986 | 7.5404 |
| 1.5 | 1.1226 | 0.4986 | 4.5406 |
| 2 | 1.2857 | 0.4986 | 2.8746 |
Table 3: Variations in skin friction, Nusselt number and Sherwood number with Q and t.
| Q (=Φ) at t=0.5 | Nu | Sh | τ |
| 0.5 | 0.8073 | 0.4377 | 0.1530 |
| 1 | 0.8026 | 0.4377 | 0.1556 |
| 1.5 | 0.8065 | 0.4377 | 0.1579 |
| 2 | 0.8169 | 0.4377 | 0.1599 |
Table 4: Variations in skin friction, Nusselt number and Sherwood number with Q and t.
| T1(=t1) at t=1.5 | Nu | Sh | τ |
| 1 | 0.6939 | 0.4986 | 12.9488 |
| 2 | 0.5488 | 0.4661 | 7.7797 |
| 2.5 | 0.4390 | 0.3729 | 6.7712 |
| 3 | 0.3658 | 0.3108 | 6.0989 |
Table 5: Variations in skin friction, Nusselt number and Sherwood number with T1 and t.
| T1(=t1) at t=0.5 | Nu | Sh | τ |
| 1 | 0.8073 | 0.4337 | 0.1530 |
| 1.5 | 0.5382 | 0.2891 | 0.1325 |
| 2 | 0.4037 | 0.2169 | 0.2753 |
| 2.5 | 0.3229 | 0.1735 | 0.3610 |
Table 6: Variations in skin friction, Nusselt number and Sherwood number with T1 and t.
| Kr att=1.5 | Nu | Sh | τ |
| 1 | 0.6939 | 0.4986 | 12.948 |
| 2 | 0.6939 | 0.6723 | 12.7890 |
| 3 | 0.6939 | 0.9394 | 12.4151 |
| 4 | 0.6939 | 1.1492 | 11.9682 |
Table 7: Variations in skin friction, Nusselt number and Sherwood number with Kr and t.
| Kr at t=0.5 | Nu | Sh | τ |
| 1 | 0.8073 | 0.4337 | 0.1530 |
| 2 | 0.8073 | 0.4881 | 0.2045 |
| 3 | 0.8073 | 0.5849 | 0.3570 |
| 4 | 0.8073 | 0.6699 | 0.5873 |
Table 8: Variations in skin friction, Nusselt number and Sherwood number with Kr and t.
| Sc at t=1.5 | Nu | Sh | τ |
| 0.22 | 0.6939 | 0.4986 | 12.9488 |
| 0.42 | 0.6939 | 0.6889 | 12.7812 |
| 0.62 | 0.6939 | 0.8370 | 12.6031 |
| 0.82 | 0.6939 | 0.9626 | 12.4050 |
Table 9: Variations in skin friction, Nusselt number and Sherwood number with Sc and t.
| Sc at t=0.5 | Nu | Sh | τ |
| 0.22 | 0.8073 | 0.4337 | 0.1530 |
| 0.42 | 0.8073 | 0.5992 | 0.5992 |
| 0.62 | 0.8073 | 0.7281 | 0.7281 |
| 0.82 | 0.8073 | 0.8373 | 0.8373 |
Table 10: Variations in skin friction, Nusselt number and Sherwood number with Sc and t.
| Gr at t=1.5 | Nu | Sh | τ |
| 0.01 | 0.6939 | 0.4986 | 12.9488 |
| 0.02 | 0.6939 | 0.4986 | 25.1820 |
| 0.03 | 0.6939 | 0.4986 | 37.4152 |
| 0.04 | 0.6939 | 0.4986 | 49.6484 |
Table 11: Variations in skin friction, Nusselt number and Sherwood number with Gr and t.
| Gr at t=0.5 | Nu | Sh | τ |
| 0.01 | 0.8073 | 0.4337 | 0.1530 |
| 0.02 | 0.8073 | 0.4337 | 0.1382 |
| 0.03 | 0.8073 | 0.4337 | 0.1235 |
| 0.04 | 0.8073 | 0.4337 | 0.1088 |
Table 12: Variations in skin friction, Nusselt number and Sherwood number with Gr and t.
| Gm at t=1.5 | Nu | Sh | τ |
| 2 | 0.6939 | 0.4986 | 12.9488 |
| 3 | 0.6939 | 0.4986 | 12.2898 |
| 4 | 0.6939 | 0.4986 | 11.6308 |
| 5 | 0.6939 | 0.4986 | 10.9718 |
Table 13: Variations in skin friction, Nusselt number and Sherwood number with Gm and t.
| Gmatt=0.5 | Nu | Sh | τ |
| 2 | 0.8073 | 0.4337 | 0.1530 |
| 3 | 0.8073 | 0.4337 | 0.5886 |
| 4 | 0.8073 | 0.4337 | 1.0242 |
| 5 | 0.8073 | 0.4337 | 1.4598 |
Table 14: Variations in skin friction, Nusselt number and Sherwood number with Gm and t.
| M1(=m1) at t=1.5 | Nu | Sh | τ |
| 0.11 | 0.6939 | 0.4986 | 12.9488 |
| 0.12 | 0.6939 | 0.4986 | 10.9715 |
| 0.13 | 0.6939 | 0.4986 | 8.9805 |
| 0.14 | 0.6939 | 0.4986 | 7.0080 |
Table 15: Variations in skin friction, Nusselt number and Sherwood number with M1 and t.
| M1(=m1) at t=0.5 | Nu | Sh | τ |
| 0.11 | 0.8073 | 0.4337 | 0.1540 |
| 0.12 | 0.8073 | 0.4337 | 0.1550 |
| 0.13 | 0.8073 | 0.4337 | 0.1562 |
| 0.14 | 0.8073 | 0.4337 | 0.1575 |
Table 16: Variations in skin friction, Nusselt number and Sherwood number with M1 and t.
| M at t=1.5 | Nu | Sh | τ |
| 1.1 | 0.6939 | 0.4986 | 2.3497 |
| 1.2 | 0.6939 | 0.4986 | 1.6780 |
| 1.3 | 0.6939 | 0.4986 | 1.1263 |
| 1.4 | 0.6939 | 0.4986 | 0.6335 |
Table 17: Variations in skin friction, Nusselt number and Sherwood number with M and t.
| M at t=0.5 | Nu | Sh | τ |
| 1.1 | 0.8073 | 0.4337 | 1.9972 |
| 1.2 | 0.8073 | 0.4337 | 1.6224 |
| 1.3 | 0.8073 | 0.4337 | 1.6224 |
| 1.4 | 0.8073 | 0.4337 | 1.3165 |
Table 18: Variations in skin friction, Nusselt number and Sherwood number with M and t.
Conclusion
The non-dimensional governing equations of the problems are solved by using Laplace transform method. The variations in the velocity, temperature and concentration with the effects of various parameters encountered in the problem are studied through graphs and the effects some of the above parameters on skin friction, Nusselt number and Sherwood number are observed.
• The velocity increases with decreasing values of (negative values) heat absorption parameter (Qor) (at t = 0.5). The velocity decreases with increasing values of heat absorption parameter (Qor) (at t=1.5).
• The fluid concentration decreases with the increasing values of chemical reaction Kr, Schmidt number various values of critical time for rampedness (t1).
• Skin friction decreases for increasing values of critical time for rampedness (t1) (at t=1.5) but reverse (at t=0.5).
• Skin friction decreases for increasing values of Hall Effect (t=1.5) but reverse (t=0.5).
References
- Chandrakala P (2011) Radiation effects on flow past an impulsively started vertical oscillating plate with uniform heat flux.Int J Dyn Fluids 7: 1–8.
- Chandram P, Sacheti NC, Singh AK (2005) Natural Convection near a vertical plate with ramped wall temperature. Heat Mass Tranasfer 41: 459-464.
- Prasad VR, Reddy NB (2008) Radiation effects on an unsteady MHD convective heat and mass transfer flow past a semi-infinite vertical permeable moving plate embedded in a porous medium. J Energy, Heat and Mass Transfer 30: 57-78.
- Chandrakala P, Bhaskar PN (2009) Thermal radiation effects on MHD flow past a vertical oscillating plate. Int. J. Applied Mechanics and Engineering 14: 349-358.
- Israel-Cookey C, Amos E, Nwaigwe C (2010) MHD oscillatory Couette flow of a radiating viscous fluid in a porous medium with periodic wall temperature. Ameri J SciIndustRes 1: 326-331.
- Jain NC, Singh H (2012) Hall and thermal radiative effects on an unsteady rotating free convection slip flow along a porous vertical moving plate. Int J of ApplMechEng 17: 53-70.
- Aurangzaib, Sharidan S (2011) Effects of Soret and Dufour on unsteady MHD flow by mixed convection over a vertical surface in porous media with internal heat generation, chemical reaction and Hall current. Canadian J SciEngg Math 2: 153-162.
- Chaudhary D, Singh H, Jain NC (2013) Effects of Hall current and thermal radiation on an unsteady free convection slip flow along a vertical plate embedded in a porous medium with constant heat and mass flux, Applied Mathematics and Physics 1: 11-26.
- Shateyi S, Mosta SS, Sibanda P (2010) The effects of thermal radiation, Hall currents, Soret and Dufour on MHD flow by mixed convection over a vertical surface in porous media, Mathematical Problems in Engineering.
- Seth GS, Nandkeolyar R, Ansari MS (2013) Effects of thermal radiation and rotation on unsteady hydro magnetic free convection flow past an impulsively moving vertical plate with ramped temperature in a porous medium. Journal of Applied Fluid Mechanics 6: 27-38.
- Shit GC, Haldar R (2010) Combined effects of thermal radiation and Hall current on MHD free-convective flow and mass transfer over a stretching sheet with variable viscosity. Physics Fluid-dynamics.
- Singh KD, Pathak R (2012) Effect of rotation and Hall current on mixed convection MHD flow through a porous medium in a vertical channel in presence of thermal radiation. Indian Journal of Pure & Applied Physics 50: 77-85.
- Takhar HS, Ram PC (1991)Â Free convection in hydro magnetic flows of a viscous heat-generating fluid with wall temperature oscillation and Hall currents. Astrophysics and Space Science 183: 193-198.
- Ahmed N, Sharma HK (2009) The radiation effect on a transient MHD flow with mass transfer past an impulsively fixed infinite vertical plate. International Journal of Applied Mathematics and Mechanics 5: 87-98.
- Rajesh V, Varma SVK (2010) Radiation effects on MHD flow through a porous medium with variable temperature or variable mass diffusion. Int. J. of Appl. Math and Mech6: 39-57.
- Vijayalakshmi AR, Kamalam AF (2013) Effects of radiation and rotation on an accelerated vertical plate with uniform mass diffusion. International Journal of Engineering Research and Technology 2: 1-9.
- Ahmed N, Kalita H, Barua DP (2010) Unsteady MHD free convective flow past a vertical porous plate immersed in a porous medium with Hall current, thermal diffusion and heat source. International Journal Engineering Science and Technology 2: 59-74.
- Ahmed N, Sarmah HK (2011) MHD transient flow past an impulsively started infinite horizontal porous plate in a rotating system with Hall current. Int. J. of. Appl. Math and Mech 7: 1-15.
- Seth GS, Nandkeolyar R, Ansari MS (2011) Effect of rotation on unsteady hydromagnetic natural convection flow past an impulsively moving vertical plate with ramped temperature in a porous medium with thermal diffusion and heat absorption. Int. J. of Appl. Math andMech 7: 52-69.
- Malique MA, Sattar MA (2005)The effects of variable properties and Hall current on steady MHD laminar convective fluid flow due to a porous rotating disk. Int J Heat and Mass Transfer 48: 4963-4972.
- Seth GS, Ansari MdS (2010) MHD natural convection flow past an impulsively moving vertical plate with ramped wall temperature in the presence of thermal diffusion with heat absorption. Int J ApplMechEngg 15: 199-215.
- Seth GS, Nandkeolyar R, Ansari MdS (2010) Hartmann flow in a rotating system in the presence of inclined magnetic field with hall effects. Tamkang Journal of Science and Engineering13: 243-252.
- Kumar A, Seth GS, Talib A (2007) Hydromagnetic Couette Flow in a Rotating System with Hall Effects, ActaCienciaIndicaXXXIII M: 937-945.
- Seth GS, Nandkeolyar R, Ansari MdS (2009) Hall Effects on Oscillatory Hydromagnetic CouetteFlow in a Rotating System. Int J Acad Res 1: 6-17.
- Kinyanjui M, Kwanza JK, Uppal SM (2001) Magneto hydrodynamic free convection heat and mass transfer of a heat generating fluid past an impulsively started infinite vertical porous plate with Hall current and radiation absorption. Energy Conversion and Management 42: 917-931.
- Cookey CA, Ogolu AO, Omubo-pepple VB (2003) Influence of viscous dissipation and radiation on unsteady MHD free convection flow past an infinite heated vertical plate in a porous medium with time dependent suction. International Journal of Heat and Mass Transfer 46: 2305-2311.
- Abo-eldahab EM, El Aziz MA (2005)Â Viscous dissipation and Joule heating effects on MHD free convection from a vertical plate with power-law variation in surface temperature in the presence of Hall and ion-slip currents. Applied Mathematical Modelling 29: 579 -595.
- Seth GS, Mahto N, Singh SK (2003) Effect of rotation on heat transfer characteristics of hydro magnetic channel flow in the presence of inclined magnetic field. Adv Math Stat Comp Methods Sci Tech 113-118.
- Seth GS (2003) Effects of Hall Current on Unsteady Hydro magnetic Couette Flow in a Rotating System. Adv Math Stat Comp Methods Sci Tech 169-174.
- Muthucumaraswamy R, Ganesan P (2003) Radiation effects on the flow past an impulsively started infinite vertical plate with variable temperature. Int J ApplMechEng 8: 125-129.
- Seth GS, Mahan MK, Ahmad N (2003) Effect of hall current on hydro magnetic free and forced convection flow in a rotating channel. Adv Math Stat Comp Methods Sci Tech 141-152.
- Seddeek AM, Aboeldahab ME (2001) Radiation effects on unsteady MHD free convection with hall current near an infinite vertical porous plate. IJMMS 26: 249–255.
- Aboeldahab EM, Elbarbary EME (2001) Hall current effect on magneto hydrodynamic free-convection flow past a semi-infinite vertical plate with mass transfer. Int J Engineering Science 39: 1641-1652.
- Kumar, Seth GS, Talib A (2003) Effect of Inclination of Applied Magnetic Field and Hall Current on Generalized Oscillatory MHD Couette Flow. Adv Math Stat Comp Methods Sci Tech 153-160.
- Das M, Mahatha BK, Nandkeolyar R, Mandal BK, Saurabh K (2014)Unsteadyhydromagnetic flow of a heat absorbing dusty fluid past a permeable vertical plate with ramped temperature. J Appl Fluid Mech 7: 485-492.
- Raju MC, Reddy NA, Varma SVK (2011) Hall-current effects on unsteady MHD flow between stretching sheet and an oscillating porous upper parallel plate with constant suction. Thermal science 15: 527-536.
- Reddy TS, Reddy OSP, Raju MC, Varma SVK (2012) MHD free convection heat and mass transfer flow through a porous medium bounded by a vertical surface in presence of Hall current. Advances in Applied Science Research 3: 3482-3490.
- Chandra RP, Raju MC, Raju GSS (2015) Thermal and Solutal Buoyancy Effect on MHD Boundary Layer Flow of a Visco-Elastic Fluid Past a Porous Plate with Varying Suction and Heat Source in the Presence of Thermal Diffusion. Journal of Applied & Computational Mathematics 4: 249.
- Vidyasagar B, Raju MC, Varma SVK (2015) Unsteady MHD Free Convection Flow of a Viscous Dissipative Kuvshinski Fluid Past an Infinite Vertical Porous Plate in the Presence of Radiation, Thermal Diffusion and Chemical Effects. Journal of Applied & Computational Mathematics 4: 255.
- Raju MC, Veeresh C, Varma SVK, Rushi Kumar B, Vijaya Kumar AG (2015) Heat and Mass Transfer in MHD Mixed Convection Flow on a Moving Inclined Porous Plate. Journal of Applied Computational Mathematics 4: 259.
Citation: Reddy LR, Raju MC, Raju GSS (2016) Convective Ramped Wall Temperature and Concentration Boundary Layer Flow of a Chemically Reactive Heat Absorbing and Radiating Fluid over a Vertical Plate in Conducting Field with Hall Current. Innov Ener Res 5: 130.
Copyright: ©2016 Reddy LR, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Usage
- Total views: 12550
- [From(publication date): 6-2016 - Aug 16, 2025]
- Breakdown by view type
- HTML page views: 11442
- PDF downloads: 1108