Research Article Open Access
Interference Effects of Excess Lithium on the Emission Signal of the Calcium and Strontium Ionic Lines during Inductively Coupled Plasma Emission Spectrometry: Simulation in Terms of the Simplified Collisional Radiative Recombination Rate Model
Mark Fungayi Zaranyika1* and Courtie Mahamadi21Professor, Chemistry Department, University of Zimbabwe, Zimbabwe
2Chemistry Department, Bindura University of Science Education, Zimbabwe
- *Corresponding Author:
- Mark Fungayi Zaranyika
Chemistry Department
University of Zimbabwe
P. O. Box MP 167 Mount Pleasant
Harare, Zimbabwe
Tel: 263-4-303211Ext.15051
E-mail: Zaranyika@science.uz.ac.zw
Received date: March 31, 2014; Accepted date: April 29, 2014; Published date: May 01, 2014
Citation: Zaranyika MF, Mahamadi C (2014) Interference Effects of Excess Lithium on the Emission Signal of the Calcium and Strontium Ionic Lines during Inductively Coupled Plasma Emission Spectrometry: Simulation in Terms of the Simplified Collisional Radiative Recombination Rate Model. J Anal Bioanal Tech 5:190 doi: 10.4172/2155-9872.1000190
Copyright: © 2014 Zaranyika MF, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Analytical & Bioanalytical Techniques
Abstract
ICP-AES Ca and Sr ion line signals were measured on 0-30 μg/mL Ca and Sr solutions, in the absence and presence of 1000 μg/mL Li as easily ionizable interferent, and the effect of the interferent on analyte calibration curve simulated using a simplified collisional radiative recombination rate model. Close agreement between experiment and theory was obtained for the full range of concentrations studied in the case of SrII, while the theoretical Ca ion line calibration curve exhibited close agreement below 10 μg/mL Ca concentration in the test solution, and a positive deviation of up to 18% from the experimental curve at higher Ca concentrations. The data obtained successfully demonstrates the potential of the simplified collisional radiative recombination rate model for simulating the effects of easily ionizable interferents on high ionization potential analytes.
Keywords
Inductively coupled plasma atomic emission spectrometry; Interference effects; Easily ionizable elements; Simplified rate model; Collisional radiative recombination; Calcium; Strontium
Introduction
The enhancement of emission lines from the analyte during inductively coupled plasma atomic spectrometry as a result of matrix effects has been reported by several workers [1-6]. A major objective of plasma diagnostics is to be able to predict or simulate the effects of interferents on analyte signal during such atomic spectrometric measurements. Recently we showed that the interference effects of easily ionizable elements, EIEs, on analyte absorbance or emission signal is given by Equation 1 [7-9]
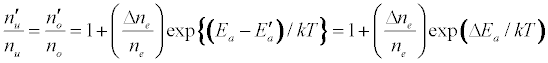
Where n denotes number density, the subscripts u and o denote analyte excited state and ground state respectively, the subscript e denotes electron, Ea denotes electron activation energy, the prime denotes quantities measured in the presence of the interferent, Δne denotes the change in the electron number density upon the introduction of the interferent, k is the Boltzmann constant and T is the absolute temperature.
the absolute temperature. It can be shown on the basis of the Boltzmann population distribution law for bound states that [9,10]:
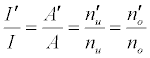
where I and A denote emission and absorbance signal intensity respectively, and the prime denotes quantities measured in the presence of the interferent as before. Substitution into Equation 1 leads to Equations 3 and 4 which can be used to predict or simulate the effects of EIE interferents on analyte calibration curve during atomic absorption and emission spectrometry respectively:
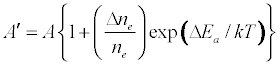
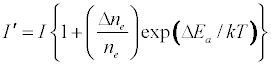
Equation 1 assumes that the effects of interferents on analyte signal arise from analyte ion – electron collisional radiative recombination [7-9,11]. Current theory of atomic spectrometry assumes local thermal equilibrium (LTE), which in turn assumes that, upon ionization, electrons are ejected with kinetic energy equal to the ionization potential of the parent atom or ion, but quickly loose this energy through thermal collisions so that at thermal equilibrium all the electrons will have kinetic energy equal to kTe, whereTe is the electron temperature corresponding to LTE conditions. Zaranyika and co-workers have shown that under the conditions of LTE, ΔEa in Equations 1, 3 and 4 is equal to zero. Experimentally ΔEa has been shown to be non-zero [7-9,11], and that during air-acetylene flame and ICP atomic spectrometry analyte ion – electron collisions occur from the ambipolar diffusion state or the LTE state, so that ΔEa is given by Equations 5 and 6 respectively:
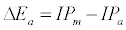
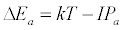
where IPm and IPa denote interferent and analyte ionization potential respectively
In a previous paper [11] we demonstrated that the Mg emission calibration curve, determined in the presence of excess Ca, Ba and Sr using air-acetylene flame atomic emission spectrometry, can be simulated with close agreement between theory and experiment using Equations 3 and 5. In this communication we report the results obtained when Equations 4 and 6 are used to simulate the effect of excess Li on the ICP-AES calibration curve for CaII and SrII. The interference effects of excess Li on CaI and SrII have been simulated before with good agreement between theory and experiment using a simplified rate model based on charge transfer between analyte ions and excited interferent atoms [12]. The charge transfer rate model differs from the collisional radiative recombination rate model in that the charge transfer rate model assumes charge transfer involving interferent electrons in bound excited states, whereas the radiative recombination rate model assumes collisions involving interferent electrons in the continuum state. The short-comings of the charge transfer rate model have been discussed previously [7], and include the fact that the charge transfer rate model is not able to explain the non-involvement of Ar species in the collisional processes leading to the observed interference effects.
Experimental
ICP equipment
A Unicam 701-Emission Inductively Coupled Argon Plasma Echelle Spectrophotometer with “crossed” dispersion was used. The spectrophotometer was fitted with an aperture plate of 90 mm by 1.5 nm slits etched at 2 mm intervals, a photomultiplier tube (PMT) detector mounted on a movable frame for radial view of the ICP, a torch with three concentric tubes for outer gas, auxiliary gas and sample transport, a 40.68 MHz R.F. generator which supplies power up to 2 kW, a grid type nebulizer fitted with Pt screens and Pt orifice, a 5-channel computer controlled peristaltic pump, and an automatic Ar gas flow rate optimizer.
The argon (99.95%) was supplied from a pressurised tank (BOC GAS Ltd, Zimbabwe): The outer gas was supplied at 14 L min-1, power 1.0 kW, nebulizer pressure 40 psi (280 kPa) and auxiliary gas at 1 L min-1. Under these conditions the plasma temperature is between 7000 and 9000 K [13]. The optimum zone for analysis was established using the strong emission line of Mn, and the maximum temperature of 9000 K was used in the calculations for maximum effect of the interferent. CaII and SrII line emission signals were recorded at 393.3 and 407.8 nm respectively.
Materials
The following were used: Calcium chloride dehydrate, M = 147.02 g/mol., AR grade (impurities present: sulphate 0.005%, total nitrogen 0.005%, phosphorous 0.001%, lead 0.001%, iron 0.0005%, magnesium 0.01%, sodium 0.01% and potassium 0.01%); Strontium chloride hexahydrate, M = 266.62 g/mol., AR grade (impurities: water insoluble matter 0.005%, sulphate 0.001%, lead 0.0002%, iron 0.0001%, zinc 0.0001%, barium 0.02%, and substances not precipitated by sulphuric acid 0.0002%); Lithium Chloride, M = 42.39 g/mol., Merck GR grade (impurities: sulphate 0.005%, total nitrogen 0.001%, heavy metals ( as lead) 0.0005%, iron 0.0005%, calcium (Ca) 0.005%, magnesium (Mg) 0.005%, sodium (Na) 0.002% and potassium (K) 0.02%) (Merck, Darmstadt, Germany); Deionised water of conductivity 0.001 μSm-1.
Procedure
The experimental procedure was described previously [7,8]. Two sets of standard solutions containing 0 to 30.0 mg/L analyte (Sr or Ca) were prepared from freshly prepared solutions of their chloride salts. One set was spiked with 1000 mg/L of LiCl as EIE interferent. The other set was left unspiked. The experiment was designed such that the interferent concentration was kept constant at a very high level (1000 mg/L) relative to that of the analyte, whilst the analyte concentration was varied. In this way changes in the physical properties of the test solution upon the introduction of the interferent could be minimized, and be compensated for by taking blank readings of a solution containing the interferent salt only. Preliminary experiments were run to determine the aspiration rate and the nebulization efficiency for the type of solutions under analysis [10,14,15]. Mean values obtained for the aspiration rate and nebulization efficiency were 1.00 ± 0.04 L/min and 5.0 ± 0.7% (n = 8) respectively
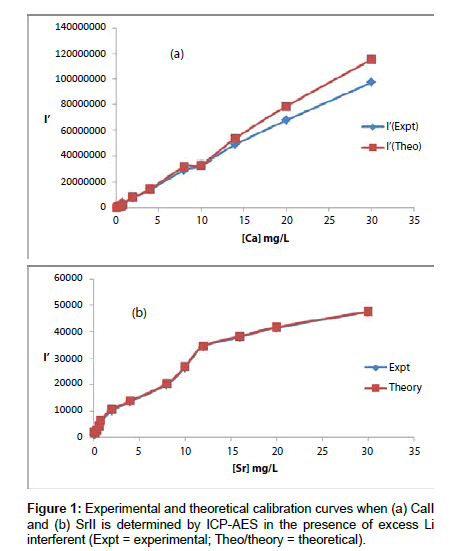
Analyte line emission signals, I and I’ where the prime denotes presence of the interferent, were read in triplicate. Typical I and I’ results obtained are shown in Table 1. The values of I’ for Ca were corrected for the contribution from contamination from the interferent, and plotted as a function of analyte concentration in the test solution in Figure 1.
| c* | CaII | SrII | ||
|---|---|---|---|---|
| [Li]= 0 mg/L | [Li]= 1000 mg/L | [Li]= 0 mg/L | [Li] = 1000 mg/L | |
| 0.0 | 142250 ± 1588 | 126216 ± 921 | ||
| 0.1 | 877 ± 11 | 1983 ±13 | ||
| 0.2 | 778553 ± 6645 | 2081694 ± 1484 | 1178 ± 10 | 2179 ± 9 |
| 0.4 | 1235614 ± 1237 | 2689027 ± 6978 | 2182 ± 33 | 3033 ± 35 |
| 0.6 | 1908893 ± 2111 | 3626017 ± 1882 | 3590 ± 58 | 4488 ± 52 |
| 0.8 | 2721784 ± 4162 | 4079534 ± 2820 | 5651 ± 46 | 6679 ± 43 |
| 2.0 | 8306215 ± 7933 | 8355747 ± 1425 | 9976 ± 122 | 11482 ± 119 |
| 4.0 | 14615291 ± 5822 | 14617597 ± 579 | 13388 ± 253 | 14606 ± 250 |
| 8.0 | 32097324 ± 1829 | 29707464 ± 2815 | 20044 ± 232 | 20986 ± 256 |
| 10.0 | 33203770 ± 1859 | 33214872 ± 4407 | 26421 ± 324 | 27399 ± 336 |
| 12.0 | 34207 ± 315 | 34789 ± 345 | ||
| 14.0 | 53349413 ± 1126 | 49002586 ± 2537 | ||
| 16.0 | 37960 ± 456 | 38909 ± 412 | ||
| 20.0 | 78537595 ± 1057 | 67945785 ± 5195 | 41483 ± 513 | 42271 ± 522 |
| 30.0 | 120000000 ± 1566 | 97605488 ± 3163 | 47523 ± 815 | 49376 ± 789 |
c = analyte concentration in test solution (mg/L)
Table 1: I and I’ values: Effect of excess Li interferent on CaII line (λ = 393.6 nm) and SrII line (λ = 407.8 nm) (n =3).
Theoretical calculations
Analyte and interferent ion number densities were calculated assuming the aspiration rate and nebulization efficiency values obtained above and 9000 K temperature. Sr+ and Ca+ number densities assumed 99.40% and 98.90% degree of ionization respectively [16], while those for Sr2+ and Ca2+ assumed 19.72% and 6.43% degree of ionization respectively [17]. The number density of Li+ ions was calculated using the Saha equation [18]:
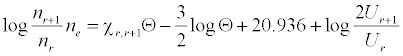
where nr and nr+1 are the number densities of atoms in the r and r+1 stages of ionization, Ne is the number density of electrons, χr, r+1 is the ionization potential in eV from the r to the r+1 stage of ionization, Θ = 5040°K/T (T = plasma temperature), Ur and Ur+1 are the partition coefficients, and the factor 2 represents the statistical weight of an electron. Number densities obtained are shown is Table 2 [19].
| M* | Flow number density (atoms/ions cm-3s-1) | ||
|---|---|---|---|
| MI | MII | MIII | |
| Ca | 2.5147 ×1010 c** | 2.46 ×1010c | 1.5818 ×109 c |
| Sr | 1.1377 ×1010 c | 1.1309 ×1010 c | 2.2301 ×109 c |
| Ar | 2.6883 ×1019 | 2.9242 ×1016 | |
| Li | 1.4367 ×1014 | 1.4367 ×1014 | |
*M = element; **c = concentration in test solution (mg/L)
Table 2: Analyte and interferent atom and ion number densities in the ICP (T =9000°C, 1.0 L.min-1, and 5.0% nebulization efficiency).
Results and Discussion
Substitution of the appropriate ionization potentials into Equation 6 yields the ΔEa values in Table 3 for CaII/Li and SrII/Li analyte/interferent systems. Substitution of the appropriate values from Tables 2 and 3 into Equation 4 yields the equations for 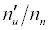 in Table 3.
in Table 3.
| Analyte | IPa (eV)a | Interferent | IPm(eV)a | ΔEa (eV) | 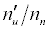 Equationb Equationb |
|---|---|---|---|---|---|
| CaII | 11.868 | Li | 5.39172 | -11.092 | 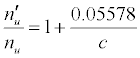 |
| SrII | 11.03013 | Li | 5.39172 | -10.255 | 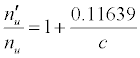 |
aSee Ref. [20]. bkT = 0.775503 eV (T = 9000°C); bc = analyte concentration in the test solution
Table 3: ΔEa values and u n n′ n equations for CaII and SrII in the ICP.
Assuming Equation 4 holds, then the emission signals in the presence of the interferent for the CaII/Li and SrII/Li analyte/interferent systems are given Equations 8 and 9 respectively:
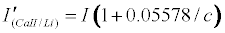
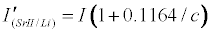
Theoretical calibration curves predicted on the basis of Eqs 8 and 9 for the effects of 1000 mg/L excess Li on CaII and SrII line emission signals in the ICP are shown in Figure 1, together with the experimental I’/I curves for comparison. It is apparent from Figure 1 that for SrII good agreement between the theoretical and experimental calibration curves is obtained throughout the range of Sr concentration studied. For CaII, good agreement is also obtained, although a negative deviation of the experimental calibration curve from the theoretical curve of up to about 18% is obtained above 10 mg/L Sr concentration in the test solution. This negative deviation of the experimental curve could be due to a drift in the plasma temperature during the course of the determinations. Errors due to system drift have been reported by Cheung et al. [20]. Otherwise, a deviation of 18% can be considered acceptable experimental error for the type of experiments under consideration.
The agreement between experiment and theory as shown in Figure 1 confirm the assumptions made in arriving at Equation 4, namely (a) that Ar species and electrons from the ionization of Ar are not involved in collisional processes leading to the observed interference effects when analytes are determined by ICP-AES in the presence of easily ionizable interferents, and (b) that collisional radiative recombination is the major collisional process leading to analyte excited state, and hence the observed interference effects [7,8]. The results obtained correspond to pre-LTE collisional radiative recombination in the absence of the interferent, and LTE collisional radiative recombination in the presence of the interferent [7-9], i.e., electronic collisions involving electrons from the ionization of the analyte occur from the ambipolar diffusion state, while collisions involving electron from the ionization of the EIE interferent occur from the LTE state after thermal equilibration. The fact that electrons from the ionization of Ar are not involved in the collisional processes leading to observed interference effects, can only be explained by assuming that collisions with these electrons occur while the electrons are still in the ambipolar diffusion layer, when their kinetic energy at 15.755 eV (i.e., the ionization potential of Ar) is far in excess of that required for radiative recombination with CaII and SrII ions. Such collisions must be elastic, otherwise the effects of collisional radiative recombination involving electrons from the ionization of the interferent, at much lower concentration in the plasma, would not be observed. The results also confirm our earlier observation [7-9] that the lifetime of electrons in the ambipolar diffusion layer appears to be inversely related to the ionization potential of the parent atom or ion. A kinetic model to account for this observation has been proposed [8]. Further work is underway in our laboratories to test the applicability of Equation 4 to other analyte/interferent systems.
Conclusion
From the foregoing discussion we conclude that interference effects due to easily ionizable elements on analyte line emission signal during ICP-AES can be simulated successfully using the simplified rate model based on collisional radiative recombination as the major collisional process leading to the observed interference effects. Although the work presented in this paper is rather limited in scope, the remarkable success of the model in predicting the interference of excess Li on the emission signal of SrII, confirms the potential of the model in simulating analyte emission signal enhancement interference effects during ICP-AES. The results presented constitute further confirmation that the ICP is not in LTE, and suggest that electrons from the ionization of easily ionizable elements exist primarily in the LTE state, while those from the high ionization potential analytes and Ar exist primarily in the ambipolar diffusion state.
Acknowledgements
Financial support for this work was provided by a grant from the Research Board of the University of Zimbabwe (UZ). The assistance of the Director and staff of the Institute of Mining Engineering, UZ, and the management and staff of Bindura Nickel Corporation, Bindura, Zimbabwe, in availing us the use of their ICP equipment is gratefully acknowledged.
References
- Blades MW, Horlick G (1981) Interference from easily ionizable element matrices in inductively coupled plasma emission spectrometry – A spatial study. Spectrochimica Acta B 36: 881-900.
- Galley PJ, Glick M, Hieftje GM (1993) Easily Ionizable Element Interferences in Inductively Coupled Plasma Atomic Emission Spectroscopy - I.; Effect on Radial Analyte Emission Patterns.Spectrochim Acta B 48: 769-788.
- Lazar AC, Farnsworth PB (1999) Matrix effect studies in the inductively coupled plasma with monodisperse droplets. Part 1: The influence of matrix on the vertical analyte emission profile.; Appl Spectrosc 53: 457-464.
- Todoli JL, Gras L, Hermandis V, Mora J (2002) Elemental matrix effects in ICP-AES: A Review. J Anal At Spectrom 17: 142-169.
- Chan GC-Y, Hieftje GM (2004) Using Matrix Effects as a Probe for the Study of the Charge-Transfer Mechanism in Inductively Coupled Plasma-Atomic Emission Spectrometry. Spectrochim Acta B 59: 163-183.
- Taylor N, Mckay-Bishop KN, Spencer RL, Farnworth PB (2014) A novel approach to understanding the effect of matrix composition on analyte emission in an inductively coupled plasma. J Anal At Spectrom 29: 644-656.
- Zaranyika MF, Chirenje AT, Mahamadi C (2012) Interference Effects of Easily Ionizable Elements in ICP-AES and Flame AAS: Characterization in terms of the Collisional Radiative Recombination Activation Energy. Spectroscopy Letters: An International Journal for Rapid Communication 45: 1-12.
- Zaranyika MF, Mahamadi C (2013) Departure from Local Thermal Equilibrium during Inductively Coupled Plasma Atomic Emission Spectrometry: Characterization in terms of Collisional Radiative Recombination Activation Energy. Pure Appl Chem 85: 2231-2248.
- Zaranyika MF, Chirenje AT, Mahamadi C (2013) Plasma Diagnostics through kinetic modeling: Characterization of matrix effects during ICP and flame atomic spectrometry in terms of collisional radiative recombination activation energy. A review. J Anal Bioanal Tech 4: 173.
- Zaranyika MF, Nyakonda C, Moses P (1991) Effect of excess sodium on the excitation of potassium in an air-acetylene flame: A steady state kinetic model which takes into account collisional excitation. Fresenius J Anal Chem 341: 577-585.
- Zaranyika MF, Chirenje AT, Mahamadi C (2012) Interference Effects of Excess Ca, Ba and Sr on Mg Absorbance During Flame Atomic Absorption Spectrometry: Characterization in Terms of a Simplified Collisional Rate Model. In Atomic Absorption Spectroscopy, Muhammad Akhyar Farrukh edition, InTech Publishers 131-142.
- Zaranyika MF, Chirenje AT, Mahamadi C (2007) Interference effects from easily ionizable elements in flame AES and ICP-OES: A possible simplified rate model based on collisional charge transfer between analyte and interferent species. Spectroscopy Letters: An International Journal for Rapid Communication 40: 835-850.
- Labexchange (1993) Unicam 701.Unicam Ltd, Cambridge, UK.
- Zaranyika MF, Makuhunga P (1997) A Possible Steady State Kinetic Model for the Atomization Process during Flame Atomic Spectrometry: Application to Mutual Atomization Interference Effects between Group I Elements. Fresenius J Anal Chem 357: 249-257.
- Zaranyika MF, Chirenje AT (2000) A possible steady state kinetic model for the atomization and excitation processes during inductively coupled plasma atomic emission spectrometry: Application to interference effects of lithium on calcium. Fresenius J Anal Chem 368: 45-51.
- Pupyshev AA, Semenova EV (2001) Formation of doubly charged atomic ions in the inductively coupled plasma. Spectrochim Acta 56B: 2397-2418.
- Blades PWJM (1987) Inductively Coupled Plasma Emission Spectroscopy, Part 2, Applications and Fundamentals. Wiley Interscience, NY.
- Allen CW (1955) Astrophysical Quantities. Athrone Press, London.
- Lide DR (1992) Handbook of Chemistry and Physics. 73rd edition, Taylor & Francis, London.
- Cheung Y, Chan GC-Y, Hieftje GM (2013) Flagging matrix effects and system drift in organic-solvent-based analysis by axial-viewing inductively coupled plasma-atomic emission spectrometry. J Anal At Spectrom 28: 241-250.
Relevant Topics
Recommended Journals
Article Tools
Article Usage
- Total views: 15389
- [From(publication date):
July-2014 - Aug 18, 2025] - Breakdown by view type
- HTML page views : 10718
- PDF downloads : 4671