Mathematical Modeling of Diffusive Transport in Vitreous Body
Received: 28-Jun-2021 / Accepted Date: 23-Aug-2021 / Published Date: 30-Aug-2021 DOI: 10.4172/1165-158X.1000202
Abstract
This research contains a mathematical model of drug distribution in the vitreous body & study about the parameter effect on injected drug concentration in the vitreous body also discussed the change in concentration profile with the time. We checked the effect of diffusion coefficient and depth of vitreous on concentration of injected drug. A prediction of model for the same initial conditions when these matched with the experimental measurements provides the concentration of drug.
Keywords: Vitreous body; Concentration profile; Computational model; Drug, Diffusion coefficient
Introduction
A few vitroretinal infections, for example, cytomegalovirus retinitis, age-related macular degeneration (AMD), retinitis pigmentosa (R.P.), diabetic retinopathy and a mix of comparable retinal illnesses are at present being treated by utilizing drug intravitreal infusion or control discharge embed of drugs. The dissemination of medication, convection of glassy outpouring, enzymatic response (digestion), binding and adequacy of delivery system fundamentally control the bioavailability of medication after its intravitreal infusion and controlled delivery embed. Numerous medications used to treat vitreoretinal sicknesses have a thin fixation range in which they are compelling and might be poisonous at higher focuses. Consequently, it is basic to know the medication conveyance inside the glassy after conveyance by intravitreal infusion or controlled deliveries embed. The capacity to anticipate drug conveyance can expand the remedial advantages and limit potential unfavorable impact, for example, conceivable tissue harm brought about by unreasonably high centralizations of medication.
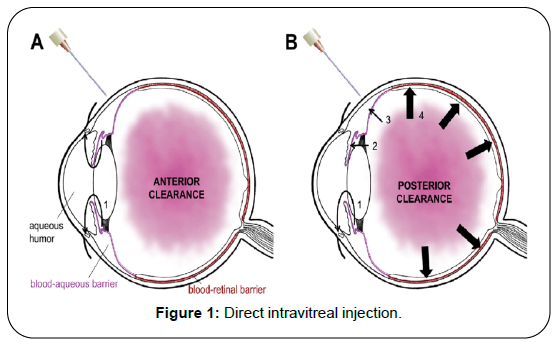
A numerical investigation of the medication fixation and hypothetical examination of the impacts of physiological boundaries on the fixation may explain the system of medication transport in the glassy and may add to the improvement of present comprehension of the bio availability of medications needed for the treatment of vitroretinal illnesses. The barrier of blood in vitreous allows the small amount of drug penetrate from blood in the vitreous body. There are lot of barriers in the way to deliver the drug retina which affects the concentration of drug distribution [1] (Figure 1).
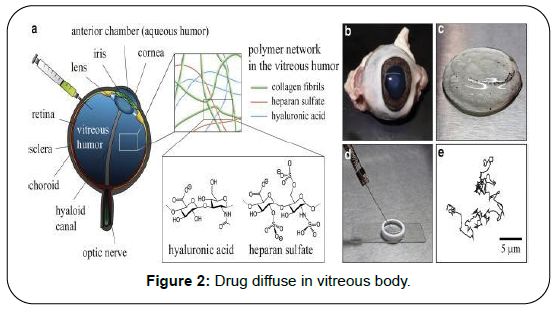
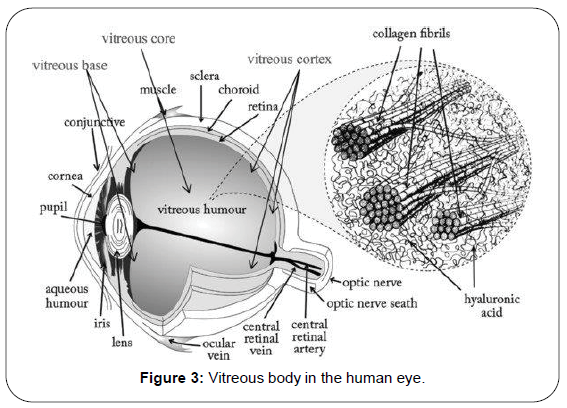
To conserve the rates of drug delivery and collect the information about the transport phenomenon is essential, for this purpose, the most important parameter is diffusion coefficient of vitreous body. To measure this we are developed an algorithm which applied for predict the rates of transport of various compounds for application to vitreous humor. For this purpose we discussed in earlier publication but we are not elaborate on that here [2]. We discussed different mechanism even this process happens similar in the eyes (Figure 2). We are focusing on diffusive transport and measurement of drug concentration and diffusion coefficient. To prepare the translation & scientific progress of drug delivery in the vitreous body, deep knowledge of transport process is very essential. Over last years the lot of progress made in numerical modeling of ocular drug delivery [3-8] (Figure 3).
There are many fatal diseases; these may affect the vitreous or retina. Eye required the treatment over long time and drug must maintained in their therapeutic window, here we are mentioning some diseases likediabetic retinopathy, Glaucoma age related macular degeneration. Now the classical methods of treatment has been changed, now a days almost are using new technique name is direct Intravitreal injection or Intravitreal implant of drug. The mathematical models play a very important role to understand the drug delivery and parameter effects on model [9-11].
The current work is worried about the improvement of a basic numerical model for the steady state concentration distribution in the vitreous body [12]. The objective of the current work was to explore the impacts of the boundaries metabolic rate and intraocular tension on the drug fixation conveyance of the intravitreally infused drugs and on change in drug focus with time in the vitreous. Other than the some other physiological parameters on the drug concentration moreover has been noticed. To explain this model, we used partial differential equations. With some exceptions, it accepted that the vitreous has little or none fluid through it, so it is true that all the ciliary body produced aqueous and the out through the anterior pathways of the eye, by using the rout of uveoscleral and the trabecular meshwork. The diffusive transport is responsible to dominate almost models of solute transport within the vitreous humor, and it is assumed that adjectives transport to be negligible. Colter et al. told about the age-related changes in the mechanical properties of the vitreous humor. More recently, Shultz et al. analyzed 190 whole human vitreous body samples extracted from donors aged 33 to 92 via shear rheology.
Mathematical Model And Solution Of Model
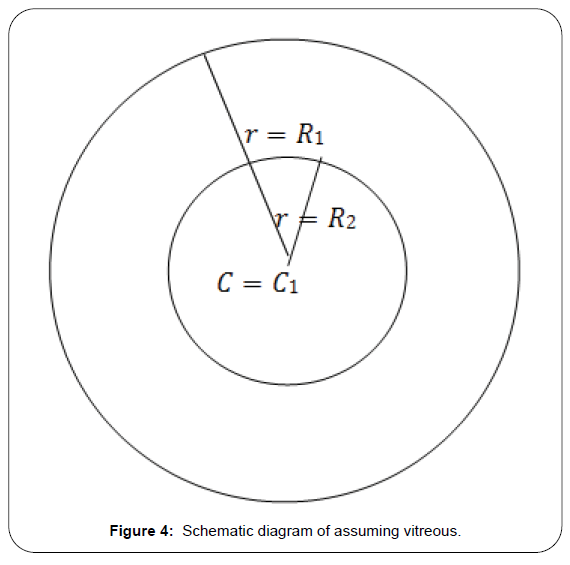
Consider the shape of vitreous is spherical and the diffusion equation in spherical redial coordinates which works as governing equation (Figure 4),
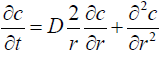 (1)
(1)
Boundary conditions
We assume that the vitreous is in spherical shape of radius R1 the surface of which is to the flux boundary condition:
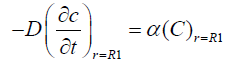 (2)
(2)
At t=0a spherical bolus of radius r=R2 having drug concentration Cα is injected in center. The initial concentration of vitreous is C=0
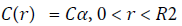 (3)
(3)
Solution of model
Let the solution of (1) is
![]()
Using (4), (1) become
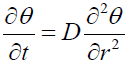 (5)
(5)
We make further substitution
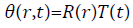 (6)
(6)
We got the solution of
T=e-pt (7)
And 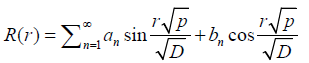 (8)
(8)
Where p is eigen values of solution as C~θr, this term is allowed in sine terms, otherwise the function will diverge to origin, and all bn are zero
Now apply boundary condition
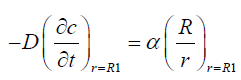 (9)
(9)
R(r) is the spital component of θ(r,t) replacing the right hand side of equation (8) for R The condition of equation (8) for each of eigen values can be express as
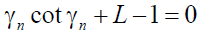 (10)
(10)
The γn roots are such that except for very short times, it is only necessary to consider the root for n=1
Where
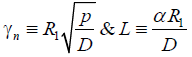 (11)
(11)
From equation (11) 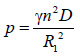
The coefficients an for each of the Eigen functions can be determine by following
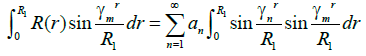 (12)
(12)
Eigen functions are orthogonal for r in the interval (0 to R1) for m=n equation (12) will be non-zero then
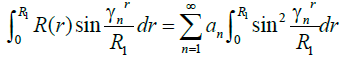 (13)
(13)
The initial condition of (6) will be transformed as Ri(r)=rCi0<r<R1 By using initial condition, an will be expressed by
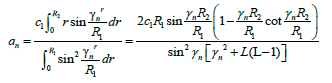 (14)
(14)
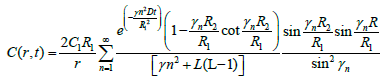 (15)
(15)
Now consider the case R2=R1. When the bolus fills the entire vitreous then equation (15) reduced as
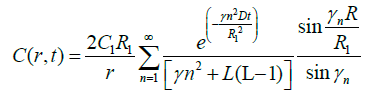 (16)
(16)
After long time, only first term have significant value. If we leave the dependency of t, so spital dependence of concentration in the established quasi-state, we have
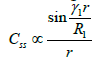 (17)
(17)
In 1991, Araie and maurice, expressed this spital dependence normalizing on concentration of drug in the centre C0 & taking limit r to zero
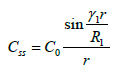 (18)
(18)
An approximation for average concentration of vitreous Cv will be obtained by the integrating equation (15) over the vireous sphere and divided by volume of vitreous and the result will be:
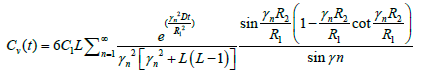 (19)
(19)
In special case R1=R2
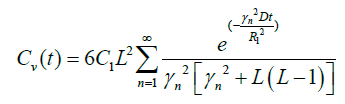 (20)
(20)
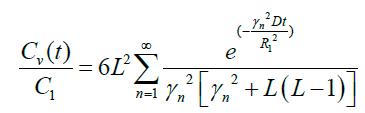 (21)
(21)
Where
Cv - Concentration of vitreous injected drug
γn - Eigen value D=Diffusion coefficient
c1 - Concentration of injected drug in bolus r-radial coordinate
Results And Discussion
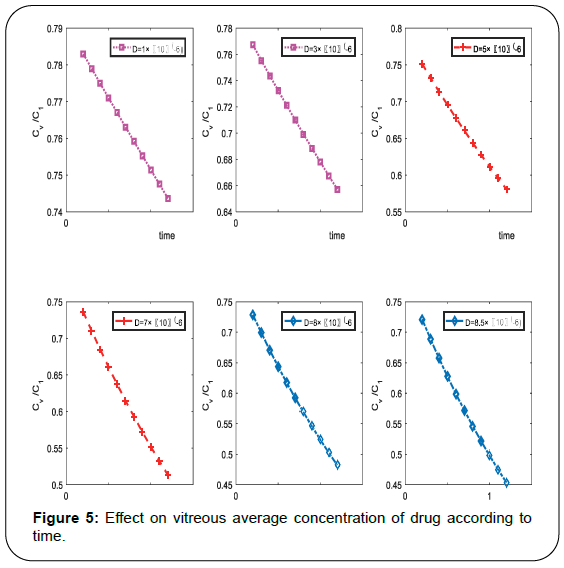
The distribution of drug concentration of injected drug and the variability in drug concentration with time at the center of vitreous are relevant for treatment of some vitro-retinal diseases such as, agerelated macular degeneration (AMD), retinitis pigmentosa, glaucoma, Rhematogeneous retinal detachment etc. Also concentration of drug depends on radius of vitreous and diffusion coefficient it also depends on γn&L and by using equation (11) we can determine the γn&L. Authors draw computational graphs and describe the effect of depth, time and diffusion on drug concentration. Plotted diagram shows that concentration profile with time for the condition such that 20μl bolus of concentration is injected on the center of vitreous which radius is 78 cm with different diffusivity constant which is occupied by the boundary condition (2). Also the value of α such that the value of L obtained by equation (10). By literature review we observed that the same values used by Araie and Maurice for fluorescein. The concentration decay mode n=1 used in equation (18), Figure 5 shows the decay modes of contribute to the vitreous concentration according to time. It shows the changes not within long time but in very short time duration it shows the sufficient decay in concentration of injected drug in the vitreous.
It is very clear from computational result, the average concertation of injected drug in vitreous is decrease according to time, it is clear that the concentration of drug is very high at the time of injected when it starts diffuse in the vitreous, it decrease as time increase. Also we conclude from above representation the concentration is sufficient effected from diffusion coefficient, as diffusivity increase the concentration decease rapidly.
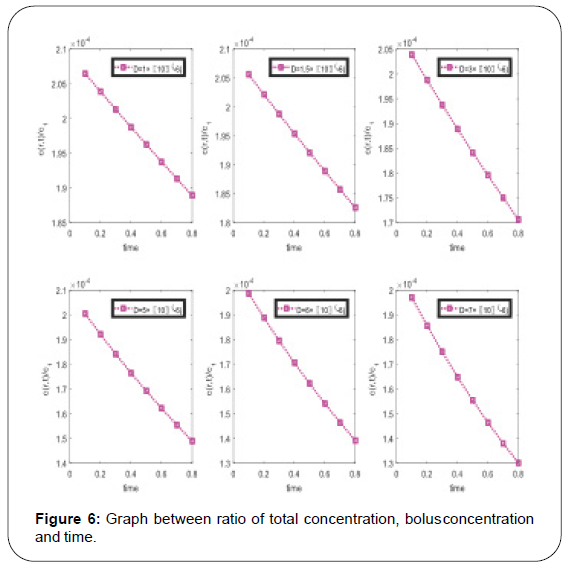
From the graphical representation in Figure 6 it is concluding remark that all concentration is decay according to time and sufficient effect of diffusion coefficient. To draw the above graphs, we use same numerical values of coefficient same as Figure 5.
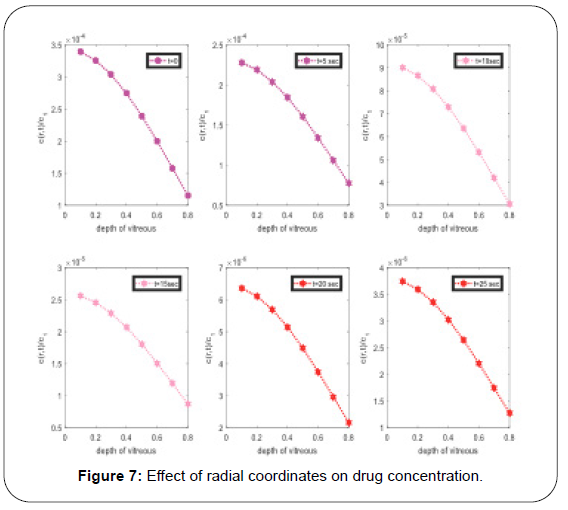
Another very important graphical representation in Figure 7, the effect of depth on injected drug concertation, it concluding remark from graphs, as the injected drug move towards to the center of vitreous, the concentration of drug which injected in vitreous decrease and at center it may reach very small. At initial stage it decrease rapidly then decrease slowly. In these graphs authors checked the effect of time on concentration, after t time it decay (Table 1).
| S .No | Epitome | Descript ion of epitome | Value of epitome | Unit | Source |
|---|---|---|---|---|---|
| 1 | D | Diffusio n coefficient | (1 - 9) × 10 | cm2/S | [13] |
| 2 | L | Constant | 3 | Dim. les | [13] |
| 3 | R | Radial coordin ates |
0. 1 - 0.77 | cm | [13] |
| 4 | R1 | Radius of vitreous body |
0.78 | cm | [13] |
| 5 | R2 | Radius of bolus |
0. 2 | cm | [13] |
Table 1: Values of constants.
Conclusion
From all above discussion we reached at following conclusion that this model is very effective to study the concentration of injected drug in the vitreous body, also derived formulae to explain the full concentration of injected drug in the eye and average concentration of injected drug in vitreous body. Finally from computational discussion, it is clear that the sufficient effect of diffusion coefficient, change in concentartion profile with respect to time and depth on concentration of injected drug in the vitreous body, during this study we discussed a very important time factor on concentration profile. This model not only used to deep study of total concentration of drug and to study of concentration of drug in the vitreous body but also retina.
Conflict of Interest
The authors have no conflict of interest.
Acknowledgement
The authors are greatfully acknowledge the constructive and fruitful comments of this research paper by reviewers of main manuscript
References
- Duvvuri, S., Majumdar, S., & Mitra, A. K.nDrug delivery to the retina: Challenges and opportunities.nExpert Opin Biol Ther., 2003;3(1): 45-56.
- Kumar, A.nMathematical Modeling of Drug Transport in vitreous humor.nInt J Pharmaceut Res., 2000;12(Sp1): 704-708.
- Kathawate, J. & Acharya, S.nComputational modeling of intravitreal drug delivery in the vitreous chambernwith different vitreous substitutes.nInt J Heat Mass Transfer., 2008;51: 5598–5609.
- Kim, S. H., Lutz, R. J., Wang, N. S., & Robinson, M. R.nTransport barriers in transscleral drug delivery for retinal diseases.nOphthalmic Res., 2007;39(5): 244-254.
- Haghjou, N., Abdekhodaie, M., Cheng, Y., & Saadatmand, M.,nComputer modeling of drug distribution after intravitreal administration.nWorld Acad Sci Eng Technol., 2011;77: 706-716.
- Stay, M. S., Xu, J., Randolph, T. W., & Barocas, V. H.nComputer simulation of convective and diffusive transport of controlled-releasendrugs in the vitreous humor.nPharm Res, 2003;20(1): 96-102.
- Ohtori, A. & Tojo, K.nIn vivo/in vitro correlation of intravitreal delivery of drugs with the help ofncomputer simulation.nBiol Pharm Bull., 1994;17(2): 283- 290.
- Balachandran, R., & Barocas, V.nComputer Modeling of Drug Delivery to the Posterior Eye: Effect of ActivenTransport and Loss to Choroidal Blood FlownPharm Res., 2008;25(11): 2685-2696.
- Balachandran, R. K., & Barocas, V. H.nComputer modeling of drug delivery to the posterior eye: effect of activentransport and loss to choroidal blood flow.nPharm Res., 2008;25(11): 2685-2696.
- Friedrich, S., Cheng, Y. L., & Saville, B.nFinite element modeling of drug distribution in the vitreous humor of the rabbitneye.nAnn Biomed Eng., 1997;25(2): 303-314.
- Pontrelli, G. & Monte F.nMass diffusion through two-layer porous media: an application to the drugelutingnstent.nInt J Heat and Mass Transfer., 2007;50(17-18): 3658-3669.
- Deepak, T., & Chader Gerald, J.nOcular Drug Delivery Systems Barriers and Application of Nano particulatenSystem scrc press. Taylor & Francis Group., 2007.
Citation: Kumar A, Seth D, Avtar R (2021) Mathematical Modeling of Diffusive Transport in Vitreous Body. Cell Mol Biol 67: 202. DOI: 10.4172/1165-158X.1000202
Copyright: © 2021 Kumar A, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Tools
Article Usage
- Total views: 2710
- [From(publication date): 0-2021 - Dec 12, 2025]
- Breakdown by view type
- HTML page views: 1907
- PDF downloads: 803