Review: Measurement Techniques for Intraocular Pressure
Received: 16-May-2016 / Accepted Date: 07-Jun-2016 / Published Date: 10-Jun-2016 DOI: 10.4172/2476-2075.1000118
Abstract
The literature on intra-ocular pressure dynamics is reviewed, including tonometer design and calibration, the influence of corneal-scleral mechanics, and scleral rigidity factors. Drugs that influence the outflow facility of the trabecular meshwork (TM) are discussed. Transmural pressure drop across the lamina cribosa (LC) is an important parameter, in terms of quantifying potential glaucoma damage to the optic nerve.
Keywords: Intraocular pressure; Glaucoma; Tonometer; Ocular rigidity; Calibration
6763Introduction
It is important to determine the intra-ocular pressure, the fluid pressure inside the eye, in order to evaluate for patients at risk from glaucoma, because of potential damage to the optic nerve [1,2]. Tonometers are calibrated to measure pressure in millimeters of mercury [mmHg]. There are many different types of tonometers, including Schiotz, Goldmann, Perkins, Marg-MacKay, Air-Puff (American Optical), and the new “Triggerfish” wireless contact lens (Sensimed AG) [3-8]. Preliminary mechanics and development work in this area was presented by Friedenwald [9]. This list is certainly not exhaustive, as there are many new devices developed in recent years, including the Tono-Pen, ocular bounce, resonant tonography, and dynamic pascal tonometry [10].
By comparison, tonographs, a different type of device can be used to measure the outflow facility. Quigley [2] reviewed the world-wide prevalence and incidence of glaucoma. Wang et al. [11-13] discussed ROP (often associated with rapid juvenile myopia rates) and glaucoma related studies.Direct and remote intra-ocular pressure measuring techniques were reviewed by Downs [14], Nuyen et al. [15], Okaforet al. [16], Sit [17], Clement et al. [18] and Stamper [19].
Basically, there are two types of tonometry, indentation and applanation (Table 1). Indentation involves corneal buckling, with attendant volumetric change ΔV, applanation involves corneal bending. Basic equations for corneal bending and buckling are listed here in Nomenclature. Various bio-mechanical factors contribute to the problem of tonometer design and calibration, including cornealscleral mechanics [20,21], aqueous outflow, diurnal fluctuations [23] and amount of axial myopia [24-27]. Nuyen et al. [15] reported 24 h fluctuations of intra-ocular pressure, measured with an instrumented contact lens.
| Type | Accuracy | Year | Area | Cost | Reference |
|---|---|---|---|---|---|
| Indentation | |||||
| (1) Schiotz | ± 2 mmHg | 1915 | 3.0 mm | $250 - $500 | [4] |
| Applanation | |||||
| (2) Goldmann | ± 1.9 mmHg | 1955 | 3.05 mm | $3,000 - 5,000 | [3] |
| (3) Perkins [Portable Goldmann] |
± 2 mmHg | 1980 | 3.0 mm | $1,380 | [5] |
| [4] Marg-MacKay | ± 1 mmHg | 1960 | 1.0 mm | n.a. | [6,28] |
| [5] Tono-Pen [Portable Marg-Mackay] |
± 2 mmHg | 1988 | 2.0 mm | $2,500 - $3,000 | [29] |
| Miscellaneous | |||||
| [6] Air-Puff | ± 1 mmHg | 1975 | n.a. | $4,000 - $8,000 | [7] |
| [7] DiatonTonom. (transpalpebral) |
± 2 mmHg | 1995 | 3.0 mm | $2,750 | [30] |
| [8] Ocular Resonance (vibration) |
± 4 mmHg | 1965 | 4.0 mm | n.a. | [31-33] |
| [9] Sensimed AG (Wireless Contact) |
± 3 mmHg | 2012 | 14 mm | $10,000 – 12,000 | [8] |
Table 1: Comparison of Tonometers.
The cornea is involved in most I.O.P. measurement methods, and its bio-mechanical properties influence the measurement results. Corneal thickness does not always correlate with corneal hysteresis. In order to properly calibrate tonometers, an evaluation of the cornea properties required new special methods [34,35].
Accommodation affects I.O.P. dynamics. The ciliary body has two main functions: regulation of the lens optical power and producing fluid. The accommodation tension is responsible for an increasing intra-ocular liquid production [36]. Eyes with progressive myopia were characterized with evident pathology of the trabecular meshwork [37,38], which reduced the aqueous outflow. The eyes with progressive myopia are distinguished with an elevated I.O.P., which possibly is a cause of the myopic eyeball extension, development of axial myopia [39], and lower than normal scleral rigidity [27].
Pierscionek et al. [40] measured scleral rigidity in the range 0.0017 to 0.0022 where K = the ratio of loge (IOP) to the change in volume, using Friedenwald’s definition. Coquart et al. [41] measured and modeled the normal-mode resonant frequencies of the pre-stressed corneo-scleral shell, a form of resonant tonometry, finding a correlation between resonant frequency and I.O.P. Woo et al. [42] measured non-linear stress-strain response of the cornea and sclera, finding that a tri-linear model worked best with the finite element technique Kobayashi et al. [43].
Literature Review
Friedenwald [9] provides provided some of the first measurements of the important “ocular rigidity” parameter [ln (mmHg)/mm3], and how that relates to the calibration and measurement of intra-ocular pressure. Nash et al. [20] reviewed corneal mechanics, measuring the Young’s modulus for cornea, an important parameter in terms of determining the effects of corneal bending and buckling. Ku et al. [21] measured the Young’s modulus for sclera, including the effects of oscillating and reverse loads, similar to the brief impulse loading during tonometry.
Modern work on new devices would include the studies of Bao et al. [44] who reported the performance of the ocular response analyser, a device for evaluating corneal hysteresis, Raina et al. [45] and Feng et al. [46], evaluated the Air-Puff tonometer, and Ottobelli et al. [47] reported on ocular resonance tonography, to measure the aqueous flow-rate through the trabecular meshwork [mm3/min]. Ophthalmologists sometimes use a water drinking test to monitor the response of the system to excess fluid intake, Yassein et al. [48].
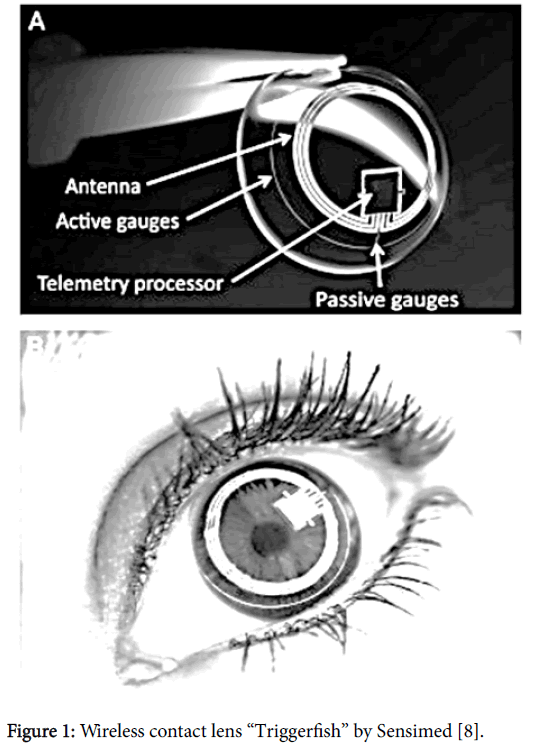
Using microfabricated strain gauges embedded in a contact lens, Zarbin et al. [8] reported measurements of circumferential changes in the area of the corneoscleral junction that indicated changes in IOP (Table 1 and Figure 1). Wireless powering and communication between the contact lens and the recording unit were achieved with a miniature microprocessor onboard the lens and a 9 mm loop antenna. This device, a miracle of modern electronics, allows continuous monitoring of fluctuations in the intra-ocular pressure, interrupted only during blinking. Transpalpebral tonometry is now possible [29], Table 1, allowing measurements through the lid, without anesthesia.
Figure 1: Wireless contact lens “Triggerfish” by Sensimed [8].
Collins [49] developed an implantable, remotely monitored pressure transducer, about the size of an aspirin tablet that was surgically inserted into the vitreous cavity, which directly and continuously measured the vitreous pressure, an important parameter in the study of glaucoma. Downs [14] reviewed the laboratory usage of similar remotely monitored intra-ocular pressure transducers. Injection of small volumes into the vitreous resulted in elevated I.O.P. [40,50].
Goyal et al. [51] used tonography to measure the aqueous outflow facility [mm3/mmHg], i.e. the flow “resistance” of the trabecular meshwork. Phillips et al. [52] used hollow rubber balls of various sizes to pre-calibrate tonometers. Coudrillier et al. [53] reviewed the effects of ageing on scleral collagen mechanical response, i.e. stiffness, an important factor with indentation tonometry. Girard et al. [54] reviewed the practical clinical applications of ocular mechanics research. The pressure drop across the lamina cribosa (LC) is an important parameter, in terms of quantifying the stress on LC fibers, Quigley [2], Hasnain [1].
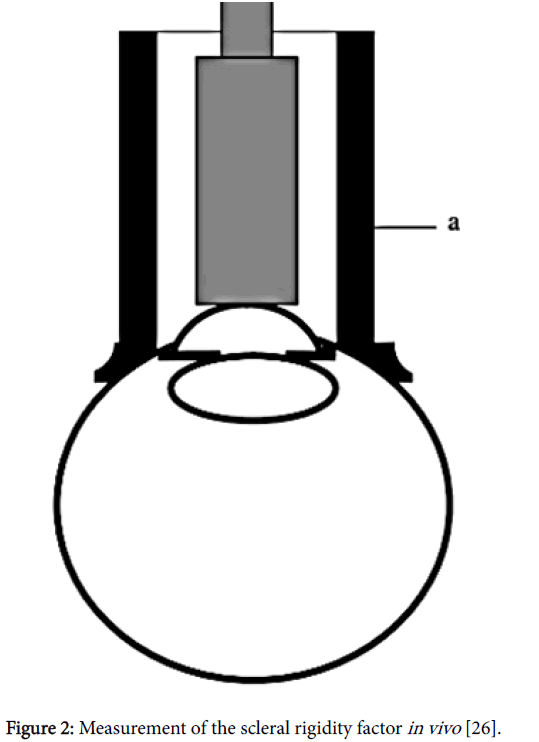
Corneo-scleral stress-strain contributions to the overall mechanical response of the globe were measured in several studies [20,21,23,25,34,35], as they related to volumetric changes induced by indentation tonometry (Figure 2). Genest et al. [55,56] modeled the chick eye with a finite element model, which simulated glaucoma with internal pressure in the range 50 to 100 mmHg or greater. Uchio et al. [57], Ljubimova et al. [58] and Coquart et al. [41] used the finite element technique to model various aspects of ocular mechanics, including accommodation, impact, and vibration.
Figure 2: Measurement of the scleral rigidity factor in vivo [26].
Silver et al. [59] reported measurements of intra-ocular volume increase with pressure increase, finding a combined linear plus logarithmic equation, showing that both logarithmic (ocular rigidity) and linear (ocular stiffness) co-efficients are present. Pallikaris et al. [60] measured ocular rigidity in living human eyes, using injected manometry, finding that ocular rigidity increases with age, and decreases with axial length.
Discussion
Scleral rigidity
Another factor of clinical importance is the amount of axial myopia, because the scleral rigidity (Figure 2) is different for high myopes [23,61,62]. Ethier et al. [63] reviewed ocular mechanics, scleral rigidity, aqueous flow parameters, etc. Bellezza et al. [64], Roberts et al. [65], and Sigal et al. [66] calculated finite element stress-strain results for the lamina cribosa (LC). Using A.P. ultrasound, Avetisov [50] and Sergienko et al. [26] measured the different mechanical properties of emmetropic and myopic eyes, reporting that the myopic eye has a lower scleral rigidity, as shown schematically in Figure 2.
Clinical applications
Accommodation dynamics and intra-ocular pressure have been suggested as relevant to the development of axial myopia and high myopia. The drug Atropine, at various concentration levels and application rates, has been explored in several clinical studies, to reduce the progressive myopia rate [67]. Tonography devices measuring the outflow facility of the trabecular meshwork (TM) are beyond the scope of this report. Commonly used drugs, used routinely with glaucoma patients for reducing the intra-ocular pressure, include Pilocarpine and Timilol. Wang et al. [13] reviewed the development of Rho-kinase, as a means of reducing intra-ocular pressure.
Conclusions
There are slight, but significant differences between various types of tonometers, some over-estimating and some under-estimating the intraocular pressure [68]. Therefore, as practiced by some ophthalmology and optometry clinics, to achieve an average and accurate results, two different instruments can be used for comparison. Generally speaking, scleral rigidity is only relevant with indentation tonometry, because the indented volume ΔV [mm3] is larger than with applanation techniques. Moses et al. [69] presented an indirect graphical technique for calculating the scleral rigidity, using several different tonometer weights. Clinical tonometry has advanced to the point where reliable measurements can be taken through the lid, or through a contact lens, thus obviating the need for corneal anesthesia, an important convenience in the modern clinic. Lastly, at present, it seems that none of these instruments were designed specifically to measure the ocular or scleral rigidity (Figure 2), parameters that may prove useful in terms of estimating patient susceptibility to axial myopia.
Nomenclature
dP = incremental increase in ocular pressure
I.O.P. = intra-ocular pressure [mmHg]
dV = incremental increase in ocular volume
K = ocular rigidity = d (ln P)/dV [mm-3]
k = ocular stiffness = dP/dV [mmHg/mm3]
Q = aqueous inflow rate [mm3/min]
c = outflow facility of the trabecular meshwork [mm3/mmHg]
Goldmann Eq. I.O.P. = (1/c) × (Q – U) + E.V.P.
E.V.P. = episcleral venous pressure
U = uveo-scleral outflow rate [mm3/min]
R (t) = axial myopia [diopters] at age t [yrs]
TM = trabecular meshwork
ROP = retinopathy of prematurity
LC = lamina cribosa ONH = optic nerve head
w = sqr [3 (1 – v2)] P a / (E × h2), corneal indentation, a = radius, h = thickness [70]
Pcrit = E * h3/(a x sqr [3 (1 – v2)]), corneal buckling, (Timoshenko et al. [70])
S crit = P crit R/2h, spherical buckling load for sclera (von Karman [22]), R = radius
1 atm. = 760 mmHg = 29.92 inch-Hg = 14.7 lb/in2 = 101.3 KPa = pressure conversions\
Conflict of Interest Statement
The authors have no proprietary or financial conflicts of interest.
References
- Hasnain SS (2016) Pathogenesis of Orderly Loss of Nerve Fibers in Glaucoma. Optom open access 1: 1-4.
- Goldmann H (1954) A new applanation tonometer. Bull MemSocFrOphtalmol 67: 474-477.
- Cridland B (1917) The tonometer of schiotz. Br J Ophthalmol 1: 352-358.
- Perkins ES (1965) Hand-held applanation tonometer. Br J Ophthalmol 49: 591-593.
- Mackay RS, Marg E, Oechsli R (1960) Automatic tonometer with exact theory: various biological applications. Science 131 :1668-1669.
- Myers KJ, Scott CA (1975) The non-contact ("air puff") tonometer: variability and corneal staining. Am J Optom Physiol Opt 52: 36-46.
- Zarbin MA, Arlow T, Ritch R (2013) Regenerative nanomedicine for vision restoration. Mayo ClinProc 88: 1480-1490.
- FriedenwaldJS (1937) Contribution to the theory and practice of tonometry. American Journal of Ophthalmology 20 :985-1024.
- Özcura F, Yildirim N, Sahin A, Çolak E (2015) Comparison of Goldmannapplanation tonometry, rebound tonometry and dynamic contour tonometry in normal and glaucomatous eyes. Int J Ophthalmol 8 :299-304.
- Wang SK, Callaway NF, Wallenstein MB, Henderson MT, Leng T, et al. (2015) SUNDROP: six years of screening for retinopathy of prematurity with telemedicine. Can J Ophthalmol 50: 101-106.
- Henderson MT, Wang SK, MoshfeghiDM (2013) A new paradigm for incorporating the joint statement screening guidelines for retinopathy of prematurity into clinical practice: outcomes from a quaternary referral program. Ophthalmic Surg Lasers Imaging Retina 44 :442-447.
- Wang SK, Chang RT (2014) An emerging treatment option for glaucoma: Rho kinase inhibitors. ClinOphthalmol 8: 883-890.
- Downs JC (2015) IOP telemetry in the nonhuman primate. Exp Eye Res 141: 91-98.
- Nuyen B, Mansouri K (2015) Fundamentals and Advances in Tonometry. Asia Pac J Ophthalmol (Phila) 4: 66-75.
- Okafor KC, Brandt JD (2015) Measuring intraocular pressure. CurrOpinOphthalmol 26: 103-109.
- Sit AJ (2014) Intraocular pressure variations: causes and clinical significance. Can J Ophthalmol 49: 484-488.
- Clement CI, Bhartiya S, Shaarawy T (2014) New perspectives on target intraocular pressure. SurvOphthalmol 59: 615-626.
- Stamper RL (2011) A history of intraocular pressure and its measurement. Optom Vis Sci 88: E16-28.
- Nash IS, Greene PR, Foster CS (1982) Comparison of mechanical properties of keratoconus and normal corneas. Exp Eye Res 35: 413-424.
- Ku DN, Greene PR (1981) Scleral creep in vitro resulting from cyclic pressure pulses: applications to myopia. Am J OptomPhysiol Opt 58: 528-535.
- Karman TV (1939) The buckling of spherical shells by external pressure. J Aeronaut Sci 7 :43-50.
- Srinivasan S, Choudhari NS, Baskaran M, George RJ, Shantha B, et al. (2016) Diurnal intraocular pressure fluctuation and its risk factors in angle-closure and open-angle glaucoma. Eye (Lond) 30: 362-368.
- Greene PR (1985) Closed-form ametropic pressure-volume and ocular rigidity solutions. Am J OptomPhysiol Opt 62: 870-878.
- Lewis JA, Garcia MB, Rani L, Wildsoet CF (2014) Intact globe inflation testing of changes in scleral mechanics in myopia and recovery. Exp Eye Res 127: 42-48.
- Sergienko NM, Shargorogska I (2012) The scleral rigidity of eyes with different refractions. Graefes Arch ClinExpOphthalmol 250: 1009-1012.
- AvetisovES, Savitskaya NF, Vinetskaya MI, Iomdina EN (1983) A study of biochemical and biomechanical qualities of normal and myopic eye sclera in humans of different age groups. MetabPediatrSystOphthalmol 7: 183-188.
- Moses RA, Marg E, Oechsli R (1962) Evaluation of the basic validity and clinical usefulness of the Mackay-Marg tonometer. Invest Ophthalmol 1: 78-85
- Minckler DS, Baerveldt G, Heuer DK, Quillen-Thomas B, Walonker AF, et al. (1987) Clinical evaluation of the OculabTono-Pen. Am J Ophthalmol 104: 168-173.
- Cacho I, Sanchez-Naves J, Batres L, Pintor J, Carracedo G (2015) Comparison of Intraocular Pressure before and after Laser In Situ Keratomileusis Refractive Surgery Measured with Perkins Tonometry, Noncontact Tonometry, and Transpalpebral Tonometry. J Ophthalmol 2015: 683895.
- Ward B (1965) Vibration tonometry and ocular rigidity. Am J Optom Arch Am AcadOptom 42: 534-548.
- Jóhannesson G, Hallberg P, Eklund A, Lindén C (2012) Introduction and clinical evaluation of servo-controlled applanation resonance tonometry. ActaOphthalmol 90: 677-682.
- Eklund A, Hallberg P, Lindén C, Lindahl OA (2003) An applanation resonator sensor for measuring intraocular pressure using combined continuous force and area measurement. Invest Ophthalmol Vis Sci 44: 3017-3024.
- Sergienko NM, Shargorodska IV (2014) Corneal biomechanical property measurement with an IOP loading method in keratoconic patients. Curr Eye Res 39: 994-999.
- Sergienko NM,Shargorodska IV (2016) Evaluation of the risk of corneal ectasia. New Front Ophthalmol 2: 52-54.
- Sergienko NM, KondratenkoIuN (1989) Accommodative hyperemia of the ciliary body as one of the pathogenetic factors in myopia. OftalmolZh : 474-476.
- Sergienko NM, KondratenkoIuN (1986) Ophthalmotonus and the gonioscopic picture in progressive and stable myopia. VestnOftalmol 102: 20-23.
- Sergienko NM, KondratenkoJN (1997) Intra ocular pressure and anterior chamber angle in patients with myopia. XI- th Congress of the European Soc of Ophthalmol Budapest 350.
- Sergienko NM, KondratenkoIuN (1988) Hypothesis of the pathogenesis of myopia. OftalmolZh : 138-143.
- PierscionekBK, Asejczyk-Widlicka M, Schachar RA (2007) The effect of changing intraocular pressure on the corneal and scleral curvatures in the fresh porcine eye. Br J Ophthalmol 91: 801-803.
- Coquart L, Depeursinge C, Curnier A, Ohayon R (1992) A fluid-structure interaction problem in biomechanics: prestressed vibrations of the eye by the finite element method. J Biomech 25:1105-1118.
- Woo SL, Kobayashi AS, Schlegel WA, Lawrence C (1972) Nonlinear material properties of intact cornea and sclera. Exp Eye Res 14: 29-39.
- Kobayashi AS, Woo SL, Lawrence C, Schlegel WA (1971) Analysis of the corneo-scleral shell by the method of direct stiffness. J Biomech 4: 323-330.
- Bao F, Huang Z, Huang J, Wang J, Deng M, et al. (2016) Clinical Evaluation of Methods to Correct Intraocular Pressure Measurements by the GoldmannApplanation Tonometer, Ocular Response Analyzer, and Corvis ST Tonometer for the Effects of Corneal Stiffness Parameters. J Glaucoma25: 510-519.
- Raina UK, Rathie N, Gupta A, Gupta SK, Thakar M (2016) Comparison of Goldmannapplanation tonometer, Tono-Pen and noncontact tonometer in children. Oman J Ophthalmol 9: 22-26.
- Feng CS, Jin KW, Yi K, Choi DG (2015) Comparison of Intraocular Pressure Measurements Obtained by Rebound, Noncontact, and GoldmannApplanation Tonometry in Children. Am J Ophthalmol160:937-943.
- Ottobelli L, Fogagnolo P, Frezzotti P, De Cillà S, et al. (2015) Repeatability and reproducibility of applanation resonance tonometry: a cross-sectional study. BMC Ophthalmol 15: 36.
- Yassein HA, Hamdi MM, Abdelshafik MA, Galal AS (2016) The Value of Water Drinking Test as a Clue for Short Term Intraocular Pressure Fluctuation. Journal of Clinical & Experimental Ophthalmology 7: 1-9.
- Collins CC (1967) Miniature passive pressure transensor for implanting in the eye. IEEE Trans Biomed Eng 14: 74-83.
- Avetisov SE, Erichev VP, Budzinskaia MV, Karpilova MA, Gurova IV, et al. (2012) Age-related macular degeneration and glaucoma: intraocular pressure monitoring after intravitreal injections. VestnOftalmol128:3-5.
- Goyal S, Beltran-Agullo L, Rashid S, Shah SP, Nath R, et al. (2010) Effect of primary selective laser trabeculoplasty on tonographic outflow facility: a randomised clinical trial. Br J Ophthalmol94:1443-1447.
- Phillips CI, Shaw TL (1970) Model analysis of impression tonometry and tonography. Exp Eye Res 10: 161-182.
- Coudrillier B, Pijanka J, Jefferys J, Sorensen T, Quigley HA, et al. (2015) Collagen structure and mechanical properties of the human sclera: analysis for the effects of age. J BiomechEng 137: 041006.
- Girard MJ, DuppsWJ, Baskaran M, Scarcelli G, Yun SH, et al. (2015) Translating ocular biomechanics into clinical practice: current state and future prospects. Curr Eye Res40:1-18.
- Genest R, Chandrashekar N, Irving E (2012) The effect of intraocular pressure on chick eye geometry and its application to myopia. ActaBioengBiomech14: 3-8.
- Genest R, Chandrashekar N, Irving EL (2013) Finite Element Model of The Chick Eye to Study Myopia. Journal of Medical and Biological Engineering 33: 215-220.
- Uchio E, Ohno S, Kudoh J, Aoki K, Kisielewicz LT (1999) Simulation model of an eyeball based on finite element analysis on a supercomputer. Br J Ophthalmol 83: 1106-1111.
- Ljubimova D, Eriksson A, Bauer S (2008) Aspects of eye accommodation evaluated by finite elements. Biomech Model Mechanobiol 7: 139-150.
- Silver DM, Geyer O (2000) Pressure-volume relation for the living human eye. Curr Eye Res 20: 115-120.
- PallikarisIG, Kymionis GD, Ginis HS, Kounis GA, Tsilimbaris MK (2005) Ocular rigidity in living human eyes. Invest Ophthalmol Vis Sci 46: 409-414.
- Perkins ES, Phelps CD (1982) Open angle glaucoma, ocular hypertension, low-tension glaucoma, and refraction. Arch Ophthalmol 100: 1464-1467.
- Perkins ES (1981) Ocular volume and ocular rigidity. Exp Eye Res 33: 141-145.
- Ethier CR, Johnson M, Ruberti J (2004) Ocular biomechanics and biotransport. Annu Rev Biomed Eng 6: 249-273.
- BellezzaAJ, Hart RT, Burgoyne CF (2000) The optic nerve head as a biomechanical structure: initial finite element modeling. Invest Ophthalmol Vis Sci 41: 2991-3000.
- Roberts MD, Sigal IA, Liang Y, Burgoyne CF, Downs JC (2010) Changes in the biomechanical response of the optic nerve head in early experimental glaucoma. Invest Ophthalmol Vis Sci51:5675-5684.
- Sigal IA, Flanagan JG, Tertinegg I, Ethier CR (2004) Finite element modeling of optic nerve head biomechanics. Invest Ophthalmol Vis Sci45:4378-4387.
- Li SM, Wu SS, Kang MT, Liu Y, Jia SM, et al. (2014) Atropine slows myopia progression more in Asian than white children by meta-analysis. Optom Vis Sci 91: 342-350.
- Galgauskas S, Strupaite R, Strelkauskaite E, Asoklis R (2016) Comparison of intraocular pressure measurements with different contact tonometers in young healthy persons. Int J Ophthalmol9: 76-80.
- Moses RA, GrodzkiWJ (1971) Theory and calibration of the Schiotz tonometer. VII. Experimental results of tonometric measurements: scale reading versus indentation volume. Invest Ophthalmol10: 716-723.
- Timoshenko SP, Woinowsky-Krieger S (1959) Theory of plates and shells. McGraw-Hill.
Citation: Greene PR, Sergienko NM, Wang SK (2016) Review: Measurement Techniques for Intraocular Pressure. Optom Open Access 1: 118. DOI: 10.4172/2476-2075.1000118
Copyright: © 2016 Greene PR, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Tools
Article Usage
- Total views: 18196
- [From(publication date): 6-2016 - Aug 20, 2025]
- Breakdown by view type
- HTML page views: 16961
- PDF downloads: 1235