Stress Analysis of Finite Steel Plate with a Rectangular Hole Subjected to Uniaxial Stress Using Finite Element Method
Received: 20-Mar-2018 / Accepted Date: 05-Jun-2018 / Published Date: 09-Jun-2018 DOI: 10.4172/2155-9910.1000254
Abstract
The orientation of a rectangular opening in a plate subject to a uniaxial stress has an important effect on stress distribution. In this paper, the effect of von mises stress has been investigated for various corner radius of rectangular opening to opening width ratio of a finite rectangular plate, from this analysis the suitable model has been selected and on the basis of that model the effect of von mises stress also has been investigated for various opening width to length ratio and from this analysis most desirable model has been selected when the value of opening width to length ratio is 0.5. Openings are reinforced to restore partially the effective cross section area and reduce stress concentration. In this paper, the effect of von mises stress on various types of reinforcements have been investigated and from this analysis it has been observed that single doubler plate gives the most suitable reinforced model. Finally, the convergence test has been performed for the most suitable reinforced model. The aim of this paper is to analyze a finite steel plate with a rectangular hole subjected to uniaxial stress and observe the effect of variation in reinforcement.
Keywords: Stress concentration; Finite element analysis; Reinforcement
Introduction
A rectangular elastic plate with central hole under static loading, have found widespread applications in various fields of engineering such as Aerospace, Marine and Automobile. For design of plates with hole, accurate knowledge of deflection and stress are required. Stress concentration arises from abrupt change in geometry of plate under static loading. As a result, stress distribution is not uniform throughout the cross section. Failures such as fatigue cracking and plastic deformations frequently occur at points of stress concentration. Since stress concentration can be a critical condition in many cases, engineers have worked on the stress concentration effect. It is, however, almost impossible to have a structure without the stress concentration effect. Our issue was not to remove the stress concentration from the structure but to minimize the effect on structures. The designer is always faced with the problem of stress concentrations at sections having abrupt changes of shape. The best that can be done is to minimize their effects. A study of the stress concentration curves for various geometries show that, in general, the sharper the corner and the larger the magnitude the change in contour, the worse will be stress concentration. The presence of holes in the structure makes it prone to stress concentration and the stress near the stress raisers becomes larger than the nominal stress by a certain amount. This stress can be found by experimental, analytical and numerical method. Though experimental methods give the most reliable results, it is very costly, as it requires special equipment’s, testing facilities etc. Analytical solution of every problem is almost impossible because of complex boundary conditions and shapes. For this reason the numerical methods had become the ultimate choice by the researchers in the last few decades. Invention and rapid improvement of the computing machines i.e. sophisticated high performance computers, also played an important role for the increasing popularity of the numerical methods.
Stress analysis of a steel structure with holes requires the solution of partial differential equations. There are various numerical methods available for the solution of partial differential equations. Among them most popular methods are Finite Element Method (FEM) and Finite Difference Method (FDM). The Finite Element Method is a numerical technique for obtaining approximate solution to a wide variety of engineering problems. FEM divides the structure in to small but finite, well defined, elements. In this analysis, finite element analysis software ABAQUS has been employed to find out the localized stresses in the plate.
Literature Review
The referenced collection of stress concentration factor data is in Peterson [1]. This book compiles the theoretical and experimental results of many researchers in to useful design charts from which the values of stress concentration kt (for normal stress), for various geometric parameters and types of loading can be read. Rorak and Young [2] also provide tables of stress concentration factors for a number of cases. The ratio of the maximum stress over the average stress computed in the critical section of the discontinuity is kt= σmax/σapp
Where σmax and σapp are the maximum stress and applied stress, respectively. The value of kt was plotted by Frocht (discussed by Beer and Johnston [3]). Amelio M. D’Arcangelo [4], investigated the variation of the maximum stress concentration factor as a function of the corner radius to the opening width ratio in a rectangular plate with a central hole. Howland [5] determined the solution of the problem of a long isotropic rectangular plate with a centered hole subject to a tension load. In plane theoretical stress concentration factors for short rectangular plates with centered circular holes subjected to uniform tension using finite element method is analyzed by Troyani N, et al. [6] .Stress concentration around a circular hole for laminated composite plate has been considered by Ko [7]. The principal cause of stress raisers like holes & notches, because concentrated stresses larger than theoretical cohesive strength will generally cause local plastic deformation and redistribution of stresses investigated by P. Stanley, B.V. Day on Stressconcentrations at an oblique hole in a thick flat plate under an arbitrary in-plane biaxial loading [8]. Abd-Elhady [9] was studied the variations of stress and strain concentration factors for plate with small central notch, circular notch and double U-notch subjected to uniaxial and biaxial loading. Mekalke et al. [10] investigated a plate with a circular hole applied to a uniform stress and examined the deviation in the results obtained through different meshes. Therefore, more study or more investigation is required to minimize the stress concentration effects of the structure. In this paper, modelling and static analysis of rectangular plate of different ratio (hole to width) has been performed.
Description of the Problem
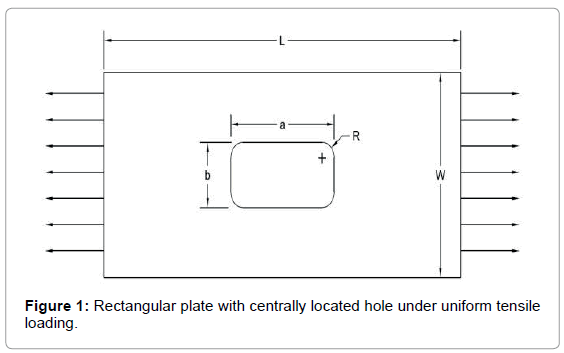
The geometry of the problem has been shown in Figure 1. The material of the plate is 0.2% C hot rolled steel; Poisson’s ratio v=0.30, Young’s modulus E=200GPa, Yield Strength Y=250MPa [11]. Plate length L=1.016 m, plate width W=1.3462 m, plate thickness t=0.00635 m. Uniform tensile load (σx) 34MPa is applied to the plate’s lengthwise direction and in this case one-quarter of the full area, with loading and boundary conditions is needed to solve stresses.
Results and Discussion
Opening in ship structures are made for access, cargo handling, passage of pipes, ducts and cables, lightening of the structure, drainage and air escape, weld relief, etc. Figure 2. Any opening in a stressed structural member, no matter how small or how well designed and fabricated, always causes a stress concentration. Ship openings that are improperly designed, poorly located, or involve bad workmanship in cutting and welding may lead to serious structural failures. To serve as a guide, some simple rules resulting from experience and experimentation will follow. These rules will deal with opening control, opening location and workmanship, rounding of the corners, relative size, shape, proportions and reinforcements Figure 3. In this section maximum Von mises stress for different corner radius to opening width ratio (r/b), opening width to length ratio (b/a) and the effect of various reinforcements of the centrally rectangular hole in the elastic plate have been determined with the help of ABAQUS. The results have been displayed with the help of graphs, tables and figures.
Effect of various corner radius to opening width ratio (r/b) on von mises stress for b/a=0.5
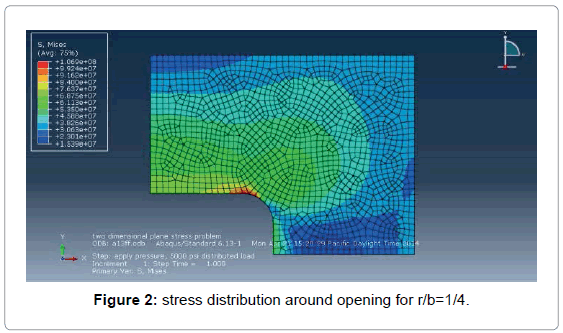
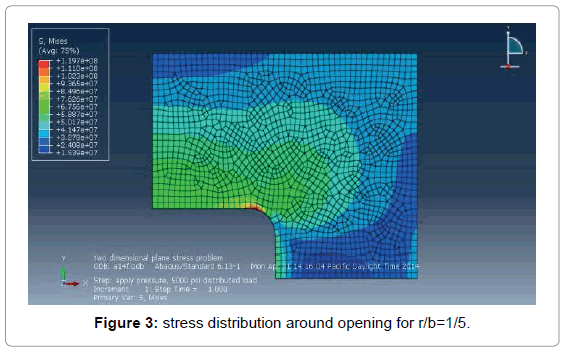
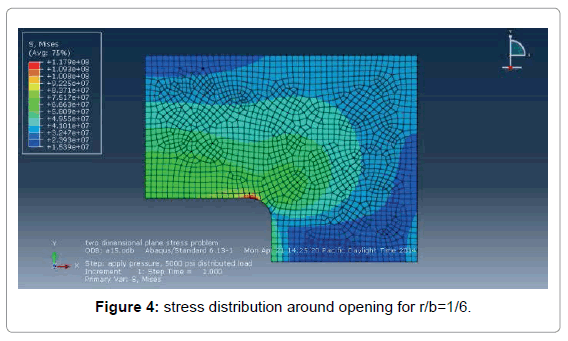
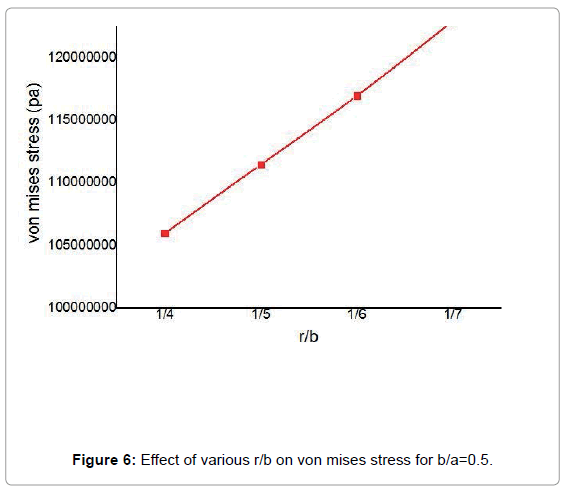
The stress concentration factor in a rectangular opening is strongly influenced by the ratio r/b. In this ratio r is the radius at the corner of the rectangular opening and b is the width of the opening Figure 4. A value of r/b between one-fourth and one-eight is used in shipbuilding. In this analysis value of r/b between one-fourth and one-seventh has been used Figure 5.
It has been observed from Figure 6 that maximum von mises stress for a central hole in a rectangular plate for r/b=1/4 is 106 MPa. The maximum von mises stress increases with the decreasing values of r/b. So, a generous corner radius is fundamental to reduce stress concentration.
Effect of various opening width to length ratio (b/a) on von mises stress for r/b=1/4
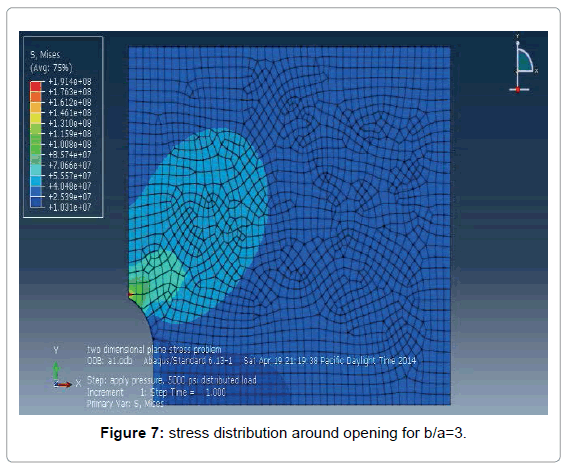
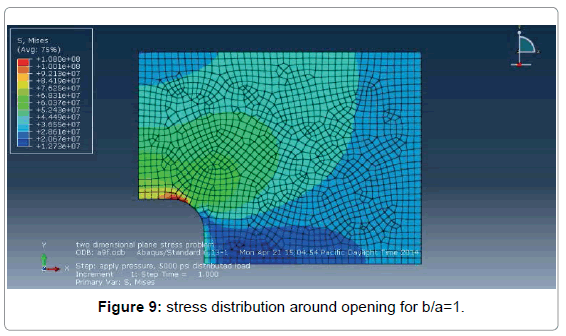
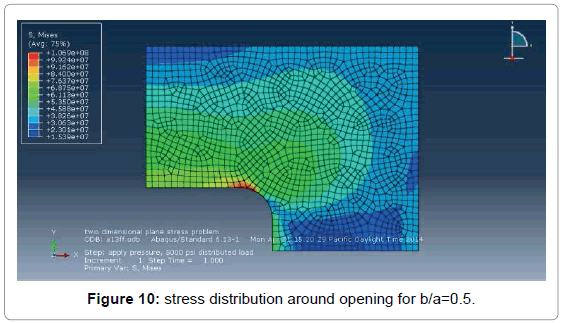
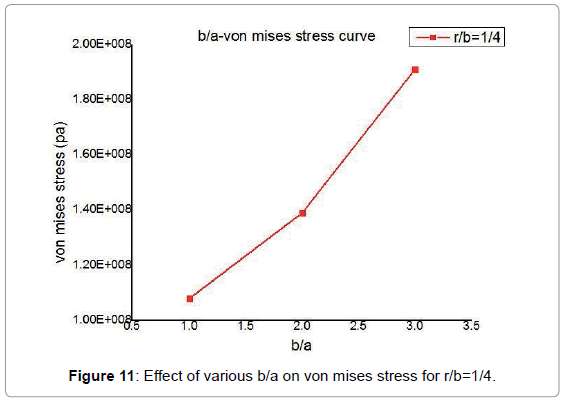
The b/a ratio of an opening in a stressed plate, has a definite influence on the value of maximum stress concentration factor Figures 7-10. Where b (opening width) is the dimension across the direction of tensile load and a (opening length) is dimension in the direction of tensile load. In this analysis value of b/a between 3 and 0.5 has been used.
It has been observed from Figure 11 that maximum von mises stress for a central hole in a rectangular plate for b/a=0.5 is 106 MPa. The maximum von mises stress increases with the increasing values of b/a. It is seen that a change of b/a from one-half to three almost doubles von mises stress. So, to keep the stress concentration factor low, it is necessary to keep the long dimensions of openings parallel to the direction of load Figure 12.
Effect of various types of reinforcements on von mises stress
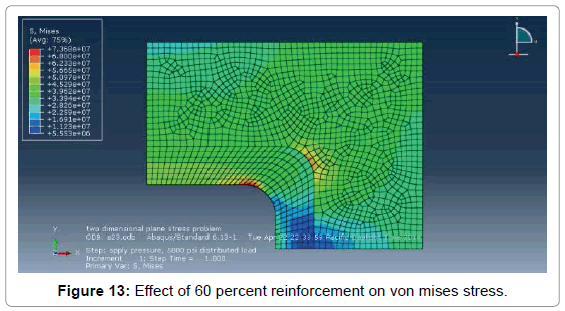
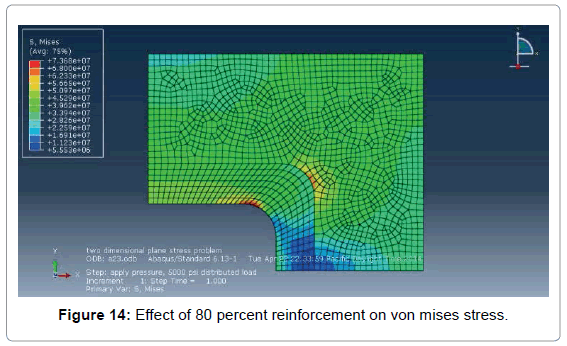
Openings are reinforced to restore partially the effective cross section area and reduce stress concentration. Actually, in way of an opening, no amount of restored material (reinforcement), however disposed, can reduce the stress concentration to unity or restore the complete strength of the uncut plate Figure 13. Three types of reinforcement are used almost exclusively in welded construction, namely: single doubler reinforcement, face bar reinforcement and insert plate reinforcement Figure 14.
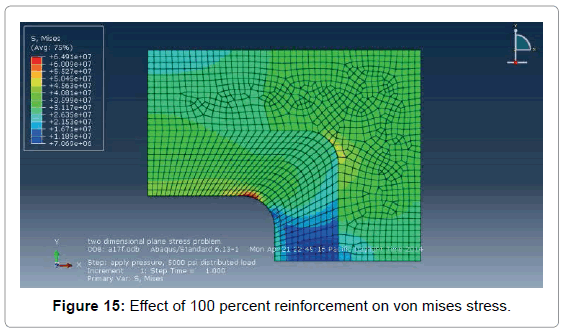
When the percentage of reinforcement will greater than the optimum indicated in Table 1, the reinforcement acted as a rigid inclusion in the body plate and failure occurred in the weld joining the outer edge of reinforcement to the body plate. In this analysis a rectangular plate with a central hole whose b/a=0.5, r/b=1/4 and maximum von mises stress was 106 MPa has been taken and various types of reinforcements have been employed Figure 15.
| Type of reinforcement | Optimum percentage |
|---|---|
| single doubler plate | 90-100 |
| Face bar | 34-40 |
| Insert plate | 30-60 |
Table 1: Optimum percentage of reinforcement.
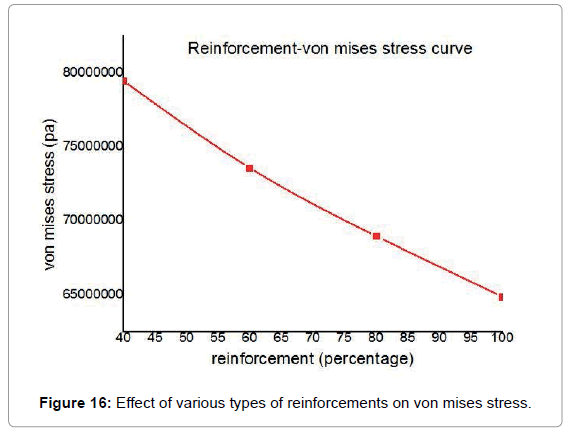
It has been observed from Figure 16 that maximum von mises stress decreases with the increase of reinforcement and maximum von mises stress for 100 percent reinforcement is 65 MPa. 100 percent reinforcement gives almost double stress than the applied stress (34 MPa). So, when the single doubler plate has been used, to obtain its maximum efficiency, it is necessary to use 90 to 100 percent reinforcement.
Effect of thickness change of reinforcement on von mises stress
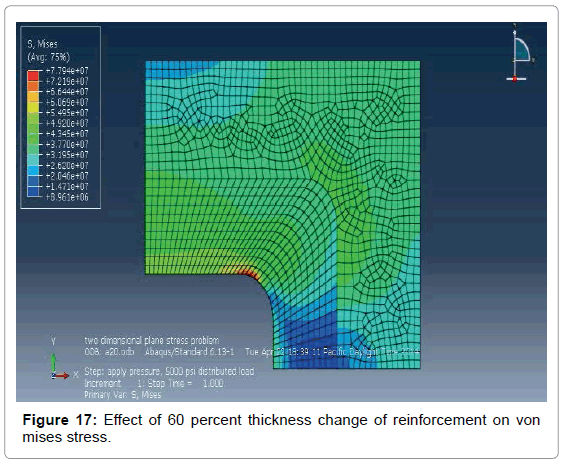
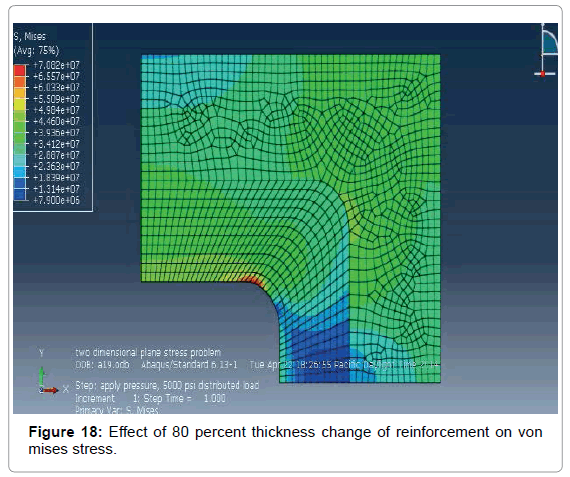
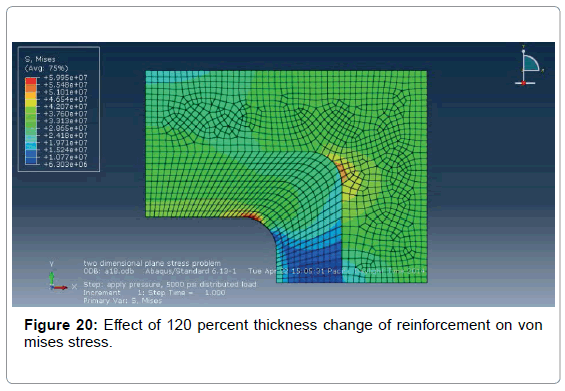
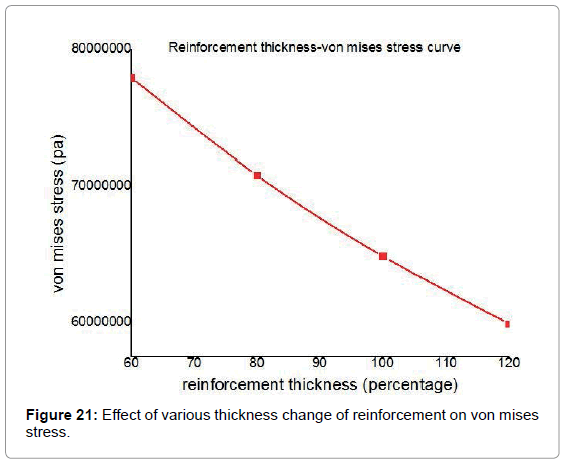
The change of thickness of reinforcement has an important effect on von mises stress. In this analysis various types of thickness are employed in the 100 percent reinforced model whose b/a=0.5, r/b=1/4 and maximum von mises stress is 65MPa Figures 17-20.
It has been observed from Figure 21 that maximum von mises stress decreases with the increase of the thickness change of reinforcement and maximum von mises stress for 120 percent thickness change of reinforcement is 59 MPa. 120 percent thickness change of reinforcement gives almost 1.75 times stress than the applied stress (34 MPa).
Mesh convergence test
It is important that to use a sufficiently refined mesh to ensure that the results from ABAQUS simulation are adequate. Coarse meshes can yield inaccurate results in analyses. The mesh is said to be converged when further mesh refinement produces a negligible change in the solution. In this analysis various types of mesh are employed in the 100 percent reinforced model whose b/a=0.5, r/b=1/4 and maximum von mises stress is 65MPa.
From Table 2 it has seen that the coarse and normal mesh predicts less accurate von mises stress due to skewness effect at the corner of the opening. The maximum von mises stress converges much more slowly because stress are calculated from displacement gradients; thus, a much finer mesh is required to predict accurate maximum von mises stress.
| Mesh | Maximum von mises stress |
|---|---|
| Coarse | 5.74E7 |
| Normal | 5.96E7 |
| Fine | 6.49E7 |
| Very fine | 6.55E7 |
Table 2: Results of mesh refinement study.
Conclusion
In this study Finite element method is used for the solution of two dimensional problems of rectangular plate having centrally located holes. Finite element results have been carried out by using commercial software ABAQUS. The following conclusions can be drawn in regard to the present study:
1. The maximum von mises stress increases with the decreasing values of r/b. So, a generous corner radius is fundamental to reduce stress concentration.
2. The maximum von mises stress increases with the increasing values of b/a. A change of b/a from one-half to three almost doubles von mises stress. So, to keep the stress concentration factor low, it is necessary to keep the long dimensions of openings parallel to the direction of load.
3. The maximum von mises stress decreases with the increase of reinforcement and 100 percent reinforcement gives almost double stress than the applied stress.
4. The maximum von mises stress decreases with the increase of the thickness change of reinforcement.
References
- Peterson RE (1974) Stress Concentration Factors, John Wiley & sons, New York.
- Rorak RJ, Young WC (1992) Formulas for Stress and Strain, 6th ed. McGraw-Hill.
- Beer FP, Johnston RJr (1992) Mechanics of Material, 2nd ed. McGraw-Hill.
- D’Arcangelo AM (1964) A Guide to Sound Ship Structures, Cornell Maritime Press, INC.
- Howland RCJ (1929) On the stresses in the neighborhood of circular hole in a strip under tension. Phil. Trans Roj Soc 229: 49-86.
- Troyani N, Gomes C, Sterlacci G (2002) Theoretical stress concentration factors for short rectangular plates with centered circular holes. Journal of Mechanical Design 124: 126-128.
- Ko W (1985) Stress concentration around a small circular hole in the Hi-Mat composite plates, NASA TM 86038.
- Stanley P, Day BV (1993) Stress concentrations at an oblique hole in a thick flat plate under an arbitrary in plane biaxial loading. Journal of strain analysis for engineering design 28: 223-235.
- Abd-Elhady AA (2014) 3-D Finite Element Analysis of Plate with Small Notch Subjected to Biaxial Loading. Emirates Journal for Engineering Research 19: 27- 35.
- Mekalke GC, Kavade MV, Deshpande SS (2012) Analysis of a Plate with a Circular Hole by FEM. IOSR J. Mech. Civil Engg 1: 25-30.
- Chandrupatala TR, Belegundu AD (2004) Introduction to Finite Elements in Engineering, 3rd ed Pearson Education.
Citation: Rahman S (2018) Stress Analysis of Finite Steel Plate with a Rectangular Hole Subjected to Uniaxial Stress Using Finite Element Method. J Marine Sci Res Dev 8: 254. DOI: 10.4172/2155-9910.1000254
Copyright: © 2018 Rahman S. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Tools
Article Usage
- Total views: 12500
- [From(publication date): 0-2018 - Dec 18, 2025]
- Breakdown by view type
- HTML page views: 11160
- PDF downloads: 1340