Influence of Cooling Constant on the Stirling Dish System Efficiency
Received: 05-Jul-2013 / Accepted Date: 27-Jul-2013 / Published Date: 02-Aug-2013 DOI: 10.4172/2157-7617.1000150
Abstract
Solar energy is the source of the most promising energy and the powerful one among renewable energies. Photovoltaic electricity (statement) is obtained by direct transformation of the sunlight into electricity, by means of cells statement. Greenius is a powerful simulation environment for the calculation and analysis of renewable power projects such as solar thermal trough power plants, photovoltaic systems, wind parks or Dish/Stirling systems. In this work, we simulated the operation of the concentrator dish Stirling, this simulation allowed us correctly to predict the influence of the meteorological parameters (direct normal insolation, ambient temperature, air density (altitude), the angle elevation of the sun, and wind speed) on the system efficiency.
Keywords: Stirling Dish System; Cooling; Simulation
11328Introduction
Solar thermal power generation utilizes the sun as a source of heat which can be exploited by concentrating that heat and using it to drive a heat engine to produce power. As such, solar thermal power generation is much more closely related to traditional forms of power generation based on fossil-fuel combustion which also rely on heat engines to convert heat into electrical energy. Current solar thermal power technologies are distinguished in the way they concentrate solar radiation, such as
a) parabolic trough systems,
b) solar tower systems and
c) solar dish systems [1].
Solar dish technology is the oldest of the solar technologies with a number of installations and operation of demonstrated solar dish systems between mid 80s and mid 90s. Solar dish systems high efficiency, high power densities, modularity, versatility, hybrid operation and their potential for long term low maintenance operation, continues to interest developers and investors in investing in solar dish technology and thus reducing their capital cost. As a result solar dish systems can provide an economical source of electricity and can become a key source of renewable energy in the coming years.
Dish/engine systems, in general, comprise a parabolic dish concentrator, a thermal receiver, and a heat engine/generator located at the focus of the dish to generate power [2]. As the thermal receiver plays a role of transferring the solar heat to the engine, and heat loss of the thermal receiver can significantly reduce the efficiency and consequently the cost effectiveness of the system, it is important to assess and subsequently improve the thermal performance of the thermal receiver [3,4].
Mathematical Model
Our software of simulation Greenius is based on the following mathematical model: the gross electrical performance is given by the equation (1): [5]
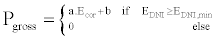 (1)
(1)
Where Ecor is the corrected irradiance inW/m2, EDNI is the direct normal irradiance inW/m2 and EDNI,min is the minimal direct normal irradiance for starting generation inW/m2.
The coefficients of the gross power are: a is performance model constant in 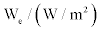 and b is the performance model constant in We .So the corrected irradiance is given by:
and b is the performance model constant in We .So the corrected irradiance is given by: 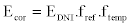 , and the correction factors are :
, and the correction factors are :
ftemp : the temperature correction factor and fref : the reflection correction factor.
The expression of the reflection correction factor is given by the equation (2):
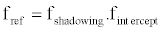 (2)
(2)
Where fshadowing is the shadowing and blockage factor and fintercept is the intercept factor. The temperature correction factor is shown in this equation (3):
 (3)
(3)
Then 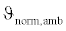 is the normalized temperature for performance model in °C and
is the normalized temperature for performance model in °C and 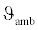 is the actual ambient temperature
is the actual ambient temperature
Or 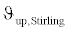 is the upper Stirling temperature in °C and the
is the upper Stirling temperature in °C and the 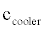 is the cooler constant in
is the cooler constant in 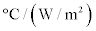
Results and Discussions
Once the gross power is obtained, the net power can be found by subtracting the parasitic power used to run the tracking, cooling, and control systems from the gross power. The net power from a Stirling dish system is given by equation (4):
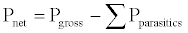 (4)
(4)
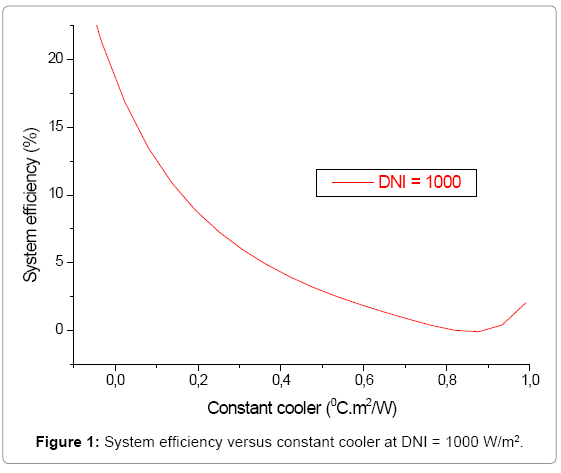
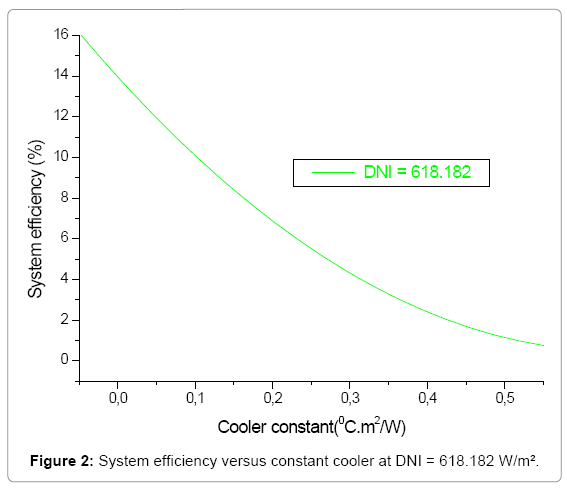
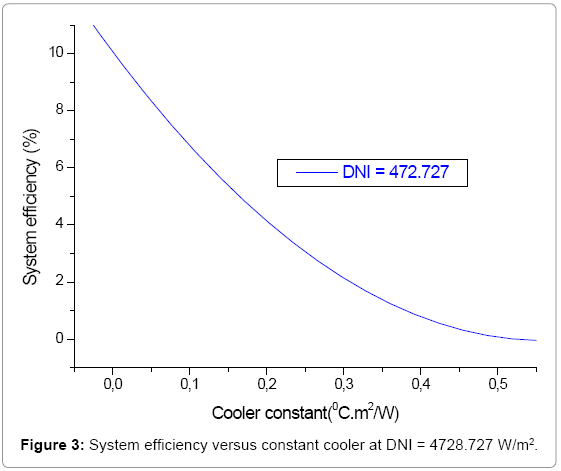
In Figures 1- 3, one notes that the system efficiency decrease with the increase in the constant of cooling until its cancellation, for great solar insolations, the constant of cooling takes lower values and consequently the important outputs.
Stirling engine cooler
The Stirling engine utilizes a cooler to reduce the temperature of the compression space and improve the engine performance. Many Stirling engine coolers use a shell-and-tube heat exchanger with the hydrogen working fluid on the tube-side and a secondary fluid on the shellside [3]. The SES engine, for instance, uses 400- 3mm diameter tubes for each of the four coolers in every cylinder with hydrogen passing within the tubes [3]. The shell-and-tube heat exchanger operates with a counter-flow heat exchange regime when the hydrogen flows from the regenerator into the compression space, and acts as a parallel-flow heat exchanger when hydrogen moves from the compression space back through the regenerator at a rate of thirty times per second. The effectiveness of the cooler and the capacitance rate of hydrogen will dictate the compression space temperature. The temperature of the engine working fluid into the cooler can be estimated by rearranging equation (5):
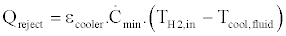
Where 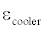 is the cooler heat exchanger effectiveness,
is the cooler heat exchanger effectiveness, 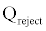 is the thermal load rejected from the Stirling engine into the cooler,
is the thermal load rejected from the Stirling engine into the cooler, 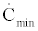 is the minimum capacitance rate of the hydrogen or cooling fluid,
is the minimum capacitance rate of the hydrogen or cooling fluid, 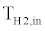 is the temperature of the hot fluid entering the cooler from the regenerator, and
is the temperature of the hot fluid entering the cooler from the regenerator, and 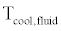 is the temperature of the cold fluid entering the cooler from the radiator loop. The temperature of the compression space can then be determined by rearranging equation (6):
is the temperature of the cold fluid entering the cooler from the radiator loop. The temperature of the compression space can then be determined by rearranging equation (6):
 (6)
(6)
Where 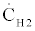 is the capacitance rate of the engine working fluid, and
is the capacitance rate of the engine working fluid, and 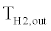 is the temperature of the compression space. The effectiveness of the cooler will vary when the capacitance rate of hydrogen or cooling fluid changes. The effectiveness-NTU relationship for a shelland- tube cooler is given by Equations (7) and (8). The UA for specific operating conditions can be determined using Equation (10) where
is the temperature of the compression space. The effectiveness of the cooler will vary when the capacitance rate of hydrogen or cooling fluid changes. The effectiveness-NTU relationship for a shelland- tube cooler is given by Equations (7) and (8). The UA for specific operating conditions can be determined using Equation (10) where  is the minimum volumetric flow rate of the hydrogen working fluid or cooling fluid during operating conditions,
is the minimum volumetric flow rate of the hydrogen working fluid or cooling fluid during operating conditions, 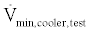 is the minimum volumetric flow rate of the hydrogen working fluid or cooling fluid during test conditions, and
is the minimum volumetric flow rate of the hydrogen working fluid or cooling fluid during test conditions, and 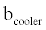 is a coefficient that is taken to be 0.7.
is a coefficient that is taken to be 0.7.
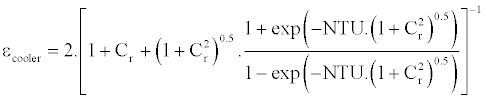 (7)
(7)
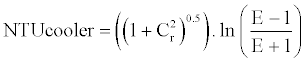 (8)
(8)
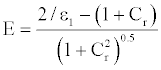 (9)
(9)
 (10)
(10)
Conclusion
A computational model was created and used to investigate the effects of system design parameters for a Stirling dish system. The model, implemented in Greenius, can be used to predict the variation of the dish Stirling system efficiency in a specific location using input weather data files. The model is expected to have greater accuracy predicting the system performance in different locations due to the additional properties of the wind velocity, sun elevation angle, and altitude. This model ideally will be used by designers to optimize design parameters and by researchers or utilities to obtain a better representation of a Stirling dish systems location specific performance.
References
- Poullikkas A (2009) Introduction to power generation technologies. Nova Science Publishers.
- Mancini TR, Kolb GJ, Chavez JM (1994) Solar thermal power todayand tomorrow. Mechanical Engineering 116: 74-79.
- Stine WB, Diver RB (1994) A compendium of solar dish/stirlingtechnology. Sandia National Laboratories.
- Stine W (1993) An international survey of parabolic dish/Stirling engineelectrical power generation technology. Solar Engineering. In: Proceedings of ASME/ASES Joint Solar Energy Conference,Washington,DC.
- Heidemann W, Drück H (2005) Institute for Thermodynamics and Thermal Engineering. University of Stuttgart, Germany.
Citation: Kaddour A, Benyouce B (2013) Influence of Cooling Constant on the Stirling Dish System Efficiency. J Earth Sci Clim Change 4: 150. DOI: 10.4172/2157-7617.1000150
Copyright: ©2013 Kaddour A, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Tools
Article Usage
- Total views: 14823
- [From(publication date): 8-2013 - Dec 09, 2025]
- Breakdown by view type
- HTML page views: 10011
- PDF downloads: 4812