A Finite Difference Model for the Thermal History of the Earth
Received: 25-Feb-2014 / Accepted Date: 05-Apr-2014 / Published Date: 08-Apr-2014 DOI: 10.4172/2157-7617.1000196
Abstract
The present study is an investigation of the thermal history of the earth using heat transfer modeling. Assuming that the earth was a hot ball at a homogeneous temperature upon its formation, the model makes the following two predictions about conditions 4.5 Ga later (the earth's approximate present age): (i) there will be a geothermal gradient within a range of 1.5-5.0 C per 100 meters in the first km of the earth crust; and (ii) the earth's crust will be about 45 km thick, which is in agreement with average continental crust thickness. The fact that oceanic crust is much thinner (around 5-10 km thick) is explained by convective heat transfer and plate tectonics. The strong agreement between the predicted thicknesses of earth's crust with the average actual continental crust thickness helps confirm the accuracy of the current inner core model of the earth indicating a solid inner core made of iron based on seismological studies.
Keywords: Thermal history; Homogenous temperature; Earth crust; Core; Geothermal gradient
7742Introduction
The first heat-diffusion model applied to the earth was Kelvin's model [1,2]. Although attempts have been made to modify Kelvin's model to account for radiogenic heating, these predictions suffer from the fact that: the model uses an estimate of the earth's initial temperature that is far below current estimates, and uses Cartesian coordinates that do not fit the geometry of the earth.
It has been suggested that the radioactive decay of uranium, thorium and potassium isotopes may be an important heat source for magma [3]. For example, the radioactive decay of plutonium 238 can produce very high temperatures. While plutonium 238 is a very active isotope, it does not occur in nature, and has a very short halflife of 87.74 years. Most radioactive isotopes that do occur naturally are much more stable and produce far less heat. However, radiogenic heating could have a significant effect due to the large amount of time between the start of the cooling to the present. According to a recent publication [4], radioactive decay could contribute to about half of earth's total heat flux. Here, we propose a model that can be used to assess the effect of factors such as radiogenic heating on the thickness of the earth's crust. We assume that that when the earth formed, it was a hot ball at a homogeneous temperature that cooled down over time via heat conduction. Solving the Fourier law in spherical coordinates should allow us to test our assumptions by making some useful predictions, such as the thickness of the earth's crust after 4.5 Ga, and earth's surface geothermal gradient.
Methods
Fourier heat diffusion model
The Fourier heat diffusion model should be expressed in spherical coordinates in order to apply to the earth. The equation in spherical coordinates is as follows:
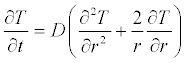 (1)
(1)
Where T is the temperature, r the radius, t the time, and D the thermal diffusivity.
In order to solve (1), we need to set the initial and boundary conditions. Consider a hot ball of radius a.
At time zero, our hot ball has a uniform temperature:
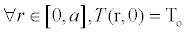 (2)
(2)
The earth's surface temperature is a constant:
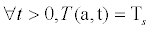 (3)
(3)
Considering a single phase system, the solution to this problem is obtained using the method of variable separation [5], and the resulting differential equation is turned into a Sturm-Liouville problem. The solution to this problem is as follows:
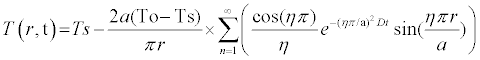 (4)
(4)
Numerical solutions are obtained by applying the summation term between n = 1 and n large enough such that (4) converges.
Still, (4) assumes a single phase system and does not account for the latent heat fusion of magma, differences in thermal diffusivity between solid and liquid magma, and radiogenic heating. In order to account for these factors, a numerical method is proposed below.
Finite-difference model of the earth's solid-liquid system
Because the cooling earth is a solid-liquid system, the latent heat fusion of magma is released when the magma crystallizes into rocks to form the crust. To model this system, we apply the finite-difference method. We use an explicit discretization scheme which is simpler to implement than the implicit scheme, although more computationally intensive for large time scale.
Equation (1) including radiogenic heating may be expressed as follows:
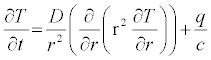 (5)
(5)
where q is the radiogenic heating in units of energy per time and mass, and c the specific heat of magma.
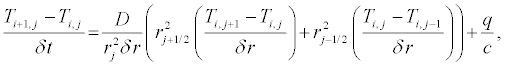 (6)
(6)
where the subscript i designates the increments in the time lattice, j the increments in the radial lattice 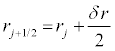 and
and 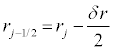 .
.
Finally we get:
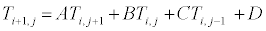 (7)
(7)
Where A, B, C and D are given in Table 1.
| When j > 0 | |
|---|---|
| A | 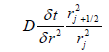 |
| B | 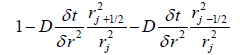 |
| C | 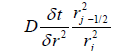 |
| D | 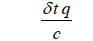 |
| When j = 0 | |
| A | 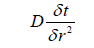 |
| B | 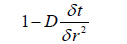 |
| C | 0 |
| D | 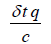 |
Table 1: Co-efficients in the explicit discretization scheme.
The stability condition for this discretization scheme is 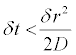
Because the cooling of the earth was concentrated primarily in its external layers, it is reasonable to consider that no cooling occurred at the earth's inner core. In addition, we assume that the inner core temperature of the earth has increased over time due to the effect of radiogenic heating. Hence, the thermal effect of radiogenic heating on the earth's inner core is expressed as follows:
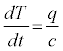 (8)
(8)
We can now compute the initial temperature of the earth, which is:
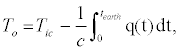 (9)
(9)
where Tic is today's inner core temperature, and the age of the earth.
In the present model we consider a time variable radiogenic heating function to account for higher radiogenic heating in the past due to the half-life disintegration of radioactive isotopes. Yet the effect of radiogenic heating remains negligible, because using today's inner core temperature as the initial temperature of the earth implies that past radiogenic heating is already factored into the model from (9).
In order to account for the latent heat fusion of magma, or the energy converted into heat during the crystallization of magma, we introduce the enthalpy which is expressed as follows:
H = ρscsT, when T<Tf (10)
H = ρscsTf +ρlcl (T-Tf)+ρh, when T<Tf (11)
where ρs and ρl are the density of the solid and liquid phases, cs and cl are the specific heat of the solid and liquid phases, h the latent heat fusion of magma, and Tf the melting point of magma.
As the cooling of the earth starts at a fully liquid phase, we introduce the energy of the latent heat fusion of magma Qi,j at each node of the lattice, which is initially set to ρh. For each incremental calculation, we then check whether Ti+1,j<Tf and Qi,j> 0. If this is the case, we first decrease Qi,j by ρcl(Tf-Ti+i,j), and if Qi+1,j is still positive, we set Ti+1,j= Tf ; otherwise, Ti+1,j = Tf +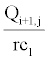 . This algorithm is equivalent to the Stefan problem. In our problem, the boundary between the solid and liquid phases is between the two adjacent nodes Ni,j and Ni,j+1, where Qi,j> 0 and Qi,j+1≤ 0. In contrast, the Stefan formulation involves solving the following equation:
. This algorithm is equivalent to the Stefan problem. In our problem, the boundary between the solid and liquid phases is between the two adjacent nodes Ni,j and Ni,j+1, where Qi,j> 0 and Qi,j+1≤ 0. In contrast, the Stefan formulation involves solving the following equation:
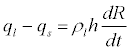 (12)
(12)
Where R is the radius at the solid-liquid interface, ql and qs are the heat fluxes in the radial direction, in liquid and solid phases respectively, at the solid-liquid interface.
When solving the above finite-difference problem, we have the ability to adapt the thermal diffusivity with the corresponding values for the solid and liquid phases depending on the state of a given node. The model can be further refined by introducing a function of the thermal diffusivity with respect to temperature given data that is available.
Parameters
Using the above model we can make predictions about the evolution of the thickness of the earth's crust at different ages. We need to input the parameters below into the model:
The thermal diffusivity of solid basalt is about 7 × 10-7 m2/s at room temperature [6], and about 5× 10-7 m2/s when close to the melting point, whereas the thermal diffusivity of molten basalt is estimated at 3× 10-7 m2/s [7]. We use the latter value for the thermal diffusivity of the liquid phase. For granite, the thermal diffusivity is about 3× 10-7 m2/s at room temperature, and 30% lower at 200°C [8]. In order to give a consistent geothermal gradient for the earth's surface, we assume that the continental crust is made up of a layer of granite to the depth where temperature is 90°C and below a layer of diffusivity comparable to basalt such as granulite. If we assume that all of earth crust's crust is made of granite, we need to put a lower limit on the thermal diffusivity of solid granite of about 7.3× 10-7 m2/s [9]. By using linear temperature dependence for the thermal diffusivity, we get:
For T< 363K: D = (19.6-0.0222T) × 10-7 m2/s
For 363 <T< 1050 K: D = (7.850.00284-T) × 10-7 m2/s
For T > 1050 K: D = 3 × 10-7 m2/s
The radiogenic heating of earth today is about 4.7 × 10-12 W/kg [10]. By taking into account the half-life of radiogenic isotopes using data in table 2 (using first-order rate kinetics for the disintegration of radioactive isotopes), the following function for radiogenic heating with respect to time is obtained:
| Uranium-238 | Thorium-232 | Potassium-40 | |
|---|---|---|---|
| Today's concentration in ppm per mass [14,15] | 0.02 | 0.08 | 130 |
| Heat generation in µW/kg [16] | 97 | 27 | 0.0036 |
| Half-life in Ga | 4.4 | 14 | 1.2 |
Table 2: Radiogenic heating data for the earth.
q(t) = 3:95 10-12exp (-0:16 t) + 2.7 × 10-12exp (-0:05 t) + 6:36 × 10-12exp (-0:58 t), where t is the time from earth's formation in Ga, and q is in units of W/kg.
The latent heat of crystallization of basaltic magma is about 4.0 105 J/kg [11].
The specific heat of basaltic magma is about 1.3 × 103 J/kg/°C
The density of basalt is about 3.0 × 103 kg/m2.
The radius of the earth is 6,371 km.
The average surface temperature of the earth is 15°C (288 K).
The inner core temperature of the earth today is 6,370 K [12]. We assume that when it formed, the earth was a hot ball of uniform temperature equal to the earth's core temperature minus the effect of radiogenic heating. Hence, using (9) and the radiogenic heating function, we obtain an initial temperature for the earth of 5,553 K.
The melting point of basaltic magma is about 700-800°C at 1 atm [13]. At 40 km below earth's surface, the pressure is about 1 GPa. By taking a melting curve slope of 5°C/kbar, at this pressure the melting point of magma is on the order of 50°C higher. For estimating the thickness of the earth's crust, let us consider a melting point of magma of 1,050 K (table 2).
Results And Discussion
Model hypotheses
A model hypothesis is that the earth's surface temperature did not change over time. This assumption may not be valid for earth's earliest years, as the surface cooled via thermal radiation until it reaches equilibrium with solar irradiation. It is reasonable to assume that the earth reached thermal equilibrium relatively quickly, and the early period of cooling therefore does not affect our predictions. The first traces of archaebacteria found in the oldest sediments in western Greenland are dated to almost 3.8 Ga [17,18]. Today, hyperthermophile Archea are found in volcanic vents, and are reported to grow at temperature between 90 and 113°C in the Mid-Atlantic Ridge [19]. The upper temperature may be used as the earth's average surface in sensitivity analysis of our model. This would lead to only small differences in our predictions. We assume that a thin crust formed on the earth in a short amount of time, on the order of a hundred Myr; hence, the age of the oldest minerals found on earth should give a reasonable estimate of the earth's age. The oldest minerals analyzed to date are crystals of zircon from Western Australia as old as 4.4 Ga [20]. The model also indicates that the earth's inner core temperature did not undergo cooling for 4.5 billion Ga; hence, taking today's inner core temperature minus the effect of radiogenic heating as the initial temperature for our problem is a reasonable assumption. Another question is: What is the effect of the water layer on the oceanic crust? The thermal diffusivity of water is about 1.4 ×10-7 m2/s, which is much lower than the thermal diffusivity of magma. The temperature at the bottom of the oceans is around 3°C [21], which may indicate that cold currents make a diffusion model inappropriate. Therefore, the oceanic water layer should not affect the prediction made by the heat-conduction model about the earth's crust.
Earth's crust thickness and surface geothermal gradient
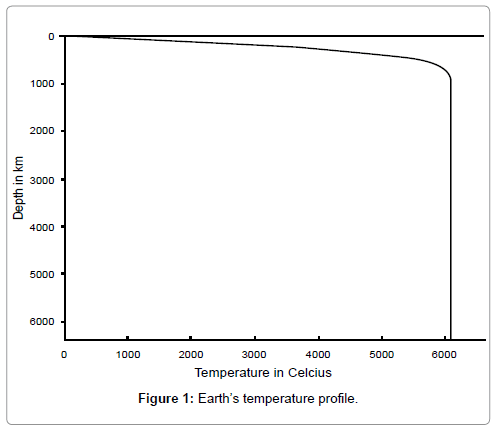
The earth's surface geothermal gradient is sensitive to our assumptions of thermal diffusivity of the earth crust. In many parts of the world, the earth's surface geothermal gradient is about 3°C per 100 meters. In order for the model to fit this value, we had to assume that the continental crust is made of granite below which lies a rock of comparable thermal diffusivity to basalt. This adjustment did not produce large changes in earth's crust thickness, which stayed between 43-45 km. The best values for the geothermal gradient in the first km of the crust are obtained by using a granite layer limited by a temperature boundary in the range of 80-135°C. Due to the coarse mesh used in the explicit discretisation scheme, it was difficult to obtain an accurate figure for the earth's surface geothermal gradient; however, values for the first km of the crust fall within a range of 1.5-5.0°C per 100 m for the granite boundaries considered. Assuming that all of the earth's crust is made of granite gave an excessively high geothermal gradient in the first km of the crust of about 13°C per 100 m. This result suggests the crust is actually made of a layer of granite, and with rocks of lower thermal diffusivity below such as gneiss, amphibolite [22] and granulite [9]. In comparison, the model envisaged for the Deccan province in India [23], consists of four layers: 8 km thick mixture of 70% magmatic gneiss with 30% granite, 9 km thick mixture of 70% tonalitic gneiss with 30% granite, 3 km thick transition layer, and 17 km thick granulite layer from top to bottom. In contrast, the present study model suggests a thin layer of pure granite of about 5 km thick, with rocks of lower thermal diffusivity below (Figure 1).
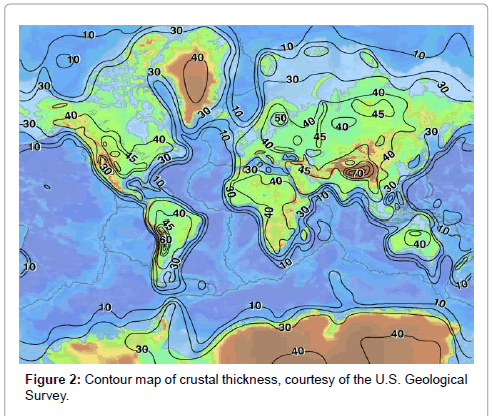
Figure 1 shows the geotherm of today's earth given by the present study model. We see that temperature increases up to a depth of 1,000 km, as only the external layer of the earth undergoes cooling. From the melting point of magma, the model indicates a crust thickness of about 45 km 4.5 Ga after the earth's formation, which is in agreement with the average thickness of the continental crust; however, the oceanic crust which covers about 60% of earth's surface is about 5 to 10 km thick, which we explain later with convection and plate tectonics. Figure 2 is a map of the crustal thickness with contour intervals of 10 km; the 45 km contour was also included for greater detail on the continents.
In Figure 2, we see two locations with anomalies in the thickness of the continental crust: the Himalaya of India, with a crust thickness of 70 km, and the Andean Cordillera of South America, with a crust thickness of 60 km. The crust thickness of the Andean Cordillera is the result of the subduction of the Nazca Plate under the South American plate. The Nazca Plate has been calibrated to be moving at a rate of 3.7 cm/year to the east, among the fastest rates of travel recorded for any tectonic plate. The thickness of the crust at the Himalaya is the result of the collision between the Indian subcontinent and Eurasia.
Excluding these anomalies, the strong agreement between the predicted thicknesses of earth's crust with the average actual continental crust thickness, helps confirm the accuracy of the current inner core model of the earth. The prediction of earth's crust thickness would fail to match the actual thickness of the continental crust, if the earth's inner core temperature deviated too far from today's estimate. This estimate is based on the iron phase diagram for the inner core composition, and seismological studies indicating a solid inner core [24,25].
The 660 km seismic discontinuity
The seismic discontinuity at 660 km depth in the earth’s mantle has been attributed to the phase change in olivine to denser silicate perovskite and magnesiowstite, respectively [26]. According to phase diagram of these components the 660 km discontinuity is assumed to take place at about 2,000 K. In contrast our thermal model of the earth indicates a temperature of 5,900 Celsius at 660 km. Recent findings of a hydrous mantle transition zone at depths between 410 and 660 km indicated by ringwoodite inclusion in a diamond from Juina, Brazil [27] could bring a new explanation to the 660 km discontinuity. The change in water content of the magma at these depths would affect viscosity of the medium resulting in a seismic discontinuity.
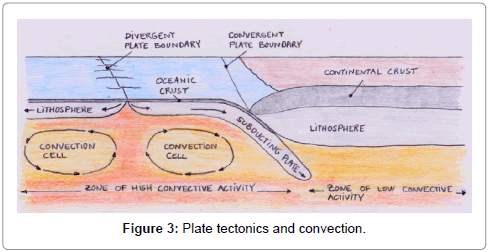
Plate tectonics of the oceanic crust and convective heat transfer
Figure 3 shows the relationship between plate tectonics and convection. At the mid ocean ridges, a divergent plate boundary occurs where the two plates slide apart from each other. At the convergence boundary between the oceanic and continental plates, a subduction zone occurs as the oceanic plate moves underneath the continental plate, where it ends up melting. The dynamics of the oceanic plates suggest convection cells in the mantle below the oceans. In contrast, the level of convective activity is much lower below the continental crust. Convection in the mantle therefore appears to explain the difference in the crust thickness between the oceanic and continental plates. Convective heat transfer brings heat from the center of the earth to the surface, causing the crust to be thinner at zones of high convective activity - a phenomenon which is not captured by a heat-conduction model. In addition, due to the lateral motion of the oceanic plates with respect to mid-ocean ridges, the renewal time of these plates is on the order of a hundred Myr. The present study mode indicates a crust thickness of about 10 km 100 Myr after formation, suggesting that the short renewal time of the oceanic plates does not allow enough time for the crust to build up.
Conclusion
The present model predicts a thickness of about 45 km for the earth's crust, 4.5 Ga after the earth's formation. This value agrees with the average thickness of the continental crust. The fact that oceanic crust is about 5 to 10 km thick is explained by convective heat transfer and plate tectonics. Convection occurring in the mantle below the oceanic plate brings heat from the interior of the earth to the surface which is not captured by a heat conduction model. In addition, the renewal time of oceanic plates is on the order of a hundred Myr, and therefore does not allow enough time for the crust to build up.
For the model to fit the geothermal gradient of 3.0°C per 100 meters for the first km of crust seen today, we had to consider the continental crust to be made of a layer of granite, and rocks of lower thermal diffusivity such as gneiss, amphibolite, and granulite below. Main sources of uncertainties with regard to model predictions arise from the difficulty of obtaining precise estimates for the input parameters. The model is particularly sensitive to the following parameters: the initial temperature of the earth, the thermal diffusivity of the liquid phase, and the effect of pressure on the melting point of magma. The model may be improved over time as more accurate estimates are obtained in the future. Yet the predicted earth's crust thickness closely agrees with actual continental crust thickness when today's estimate of the inner core temperature was used to compute the initial temperature. This estimate was based on seismological studies indicating a solid inner core made of iron. In conclusion, our model corroborates today's inner core model of the earth.
References
- Harrison TM (1987) Comment on Kelvin and the age of the earth. J Geol 95: 725-727.
- Jochum KP, Hofmann AW, Ito E, Seufert HM, White WM (1983) KU and Th in mid-oceanridgebasalt glasses and heat production, K/U and K/Rb in the mantle. Nature 306: 431-436.
- Gando A, Gando Y, Ichimura K, Ikeda H, Inoue K, et al. (2011) Partial radiogenicheat model for Earth revealed by geoneutrinomeasurements. Nature Geosci 4: 647-651.
- Sirousazar M, Mohammadi-Doust A, Achachlouei BF (2009) Mathematical Investigation of the Effects of Slicing on the OsmoticDehydration of Sphere and CylinderShaped Fruits. Czech J Food Sci 27: 95-101.
- Ruether J (2011) The validation of the LMC device: Analysis of Icelandicbasalticrocks. Master'sthesis, The School for RenewableEnergy Science, in affiliation with the University of Iceland and University of Akureyri, Iceland.
- Whittington AG, Hofmeister A, Nabelek PI, Galenas MG, Romine, WL (2009) Thermal Diffusivity of Magmas: Implications for Heat Transport in PartiallyMolten Zones. Am Geophy Union, Fall Meeting, USA.
- Kim J, Lee Y, Koo M (2007) Thermal Properties of Granite fromKorea. American Geophysical Union, Fall Meeting, USA.
- Seipold U, Gutzeit W (1982) The distribution of thermal diffusivity in the Earth crust. Physics Earth PlanetaryInteriors 29: 69-72.
- Jaupart C, Labrosse S, Mareschal JC (2007) Temperature, Heat and Energy in the Mantle of the Earth. D. Bercovici (edn.). Mantle Dynamics - Treatise on Geophysics, Elsevier 7: 253-303.
- Kuritani T, Yokoyama T, Nakamura E (2007) Rates of Thermal and Chemical Evolution of Magmas in a Cooling Magma Chamber: A Chronological and TheoreticalStudy on Basaltic and Andesitic Lavas fromRishriVolcano, Japan. J Petrol 48: 1295-1319.
- Alfe D, Gillian MJ, Price GD (2003) Thermodynamicsfrom first principle: temperature and composition of the Earth'score. Mineralogical Magazine 67: 113-123.
- McDonough WF, Sun S (1995) The composition of the Earth. Chem Geol 120: 223-253.
- Stacey FD, Davis MP (2008) Physics of the earth. Cambridge UniversityPress, UK.
- Clauser C (2009) Heat Transport Processes in the Earth'sCrust. Survey in Geophysics 30: 163-191.
- Hahn J, Haug P (1986) Traces of archaebacteria in ancientsediments. System Appl Microbiol 7: 178-183.
- Chappe B, Albrecht P, Michaelis W (1982) Polar lipids of archaebacteria in sediments and petroleums. Sci 217: 65-66.
- Blochl E, Rachel R, Burggraf S, Hafenbradl D, Jannasch HW, et al. (1997) Pyrolobusfumarri, gen. and sp. Novrepresents a novel group of archaea, extending the uppertemperaturelimit for life to 113 C. Extremophiles 1: 14-21.
- Wilde SA, Valley JW, Peck WH, Graham CM (2001) Evidence fromdetrital zircons for the existence of continental crust and oceans on the Earth 4.4 Gyrago. Nature 409: 175-178.
- Groves DG (1989) The Oceans: A Book of Questions and Answers. John Wiley and Sons, USA.
- Seipold U, Huenges E (1998) Thermal properties of gneisses and amphibolites - height pressure and high temperature investigations of KTB-rock samples. Teconophysics 291: 173-178.
- Roy S, Rao RM (1999) Geothermal investigations in the 1993 Laturearthquake area, Deccan Volcanic Province, India. Tectonophysics 306: 237-252.
- Engdahl ER, Flynn EA, Masse RP (1974) DifferentialPkiKPtravel times and the radius of the core. Geophysical J Royal Astro Soc 40: 457-463.
- Monnereau M, Calvet M, Margerin L, Souriau A (2010) LopsidedGrowth of Earth'sInnerCore. Sci 328: 1014-1017.
- Boehler R (1996) Meltingtemperature of the earth’smantle and core: Earth’s Thermal Structure. Annu Rev Earth Planet Sci 24: 15-40.
- Pearson DG, Brenker FE, Nestola F, McNeill J, Nasdala L, et al. (2014) Hydrousmantle transition zone indicated by ringwoodite includedwithindiamond. Nature 507: 221-224.
Citation: Heymann Y (2014) A Finite Difference Model for the Thermal History of the Earth. J Earth Sci Clim Change 5: 196. DOI: 10.4172/2157-7617.1000196
Copyright: © 2014 Heymann Y. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Tools
Article Usage
- Total views: 15113
- [From(publication date): 7-2014 - Aug 18, 2025]
- Breakdown by view type
- HTML page views: 10510
- PDF downloads: 4603