A New Approach of Solving the Nonlinear Equations in Biofiltration of Methane in a Closed Biofilter
Received: 26-May-2018 / Accepted Date: 31-May-2018 / Published Date: 04-Jun-2018 DOI: 10.4172/2155-9872.1000405
Keywords: New homotopy perturbation method; Mathematical modeling; Nonlinear equations; Biofiltration; Methane; Carbon dioxide
Nomenclature
A: Specific surface of the packing material (m2/ m3); CP: Concentration of P within the gas phase (g/m3); D: Biofilter inlet diameter (m); DP: Diffusion coefficient of P in the biofilm (m2/s); EC: Elimination Capacity (g/m3/h); H: Height of the packing material within the biofilter (m); HP: Henry coefficient of P (dimensionless); SCH4 : Concentration of methane in the biofilm phase; SCO2 : Concentration of carbon dioxide in the biofilm phase; 4 CCH : Concentration of methane in the gas phase; CCO2 : Concentration of carbon dioxide in the gas phase; DCH4 : Diffusion coefficient of methane in the biofilm; DCO2 : Diffusion coefficient of carbon dioxide in the biofilm; IL: Inlet Load (g/m3/h) in inlet flow; k(T): Maximum substrate utilisation rate at a T Temperature (1/s); Km: Monod Constant (g/m3) out outlet flow; P: CH4 or CO2; Pendo: Endogenous Production of CO2 (g/m3/h); PCO2: CO2 Production (g/ m3/h); Q: Gas Flow Rate (m3/h); r: CH4 Consumption rate (g/m3 (filter bed)/s); SP: Concentration of P within the Biofilm (g/m3); T: Time (s); T: Temperature (°C); ug: Gas Superficial velocity within the Biofilter (m3/ m2/s); V: Biofilter Bed Volume (m3); x: Depth coordinate in the Biofilm (m); Xb: Density of Biomass in the Biofilm (g/m3); X: Conversion (%); Y: Biomass Yield Coefficient (g biomass/gCH4); z: Biofilter Height Coordinate (m).
Greek symbols
αCO2 /CH : Yield of CO2 (g gaseous CO2 produced/gCH4 consumed); δ: Biofilm thickness (m); ε: Filter bed porosity (dimensionless); μ: Specific growth rate of the microorganisms within the biofilm (1/s); μm: Maximum specific growth rate of microorganisms within the biofilm (1/s); σ: CH4 Consumption rate (g/m3 (filter bed)/s); θ: Temperature Coefficient (dimensionless).
Introduction
A methane is assimilated by the methanotrophs: these bacteria use the methane as their sole and unique carbon source to satisfy their metabolic needs. In addition to the methanotrophic population, the availability of nutrients (mainly as nitrogen and phosphorus elements) and supportive operating conditions, such as the moisture of the packing material, the gas superficial velocity and the inlet CH4 concentration, are all to be accounted for among the factors needing to be closely controlled for operating a successful bioprocess. During the past 3 decades, several mathematical models dealing with the biofiltration of pollutants, such as volatile organic or inorganic compounds, have been developed in order to predict the efficiency of the bioprocess and the behaviour of the pollutants, and products. In general, models take into account physical, chemical and biological phenomena occurring in biofilteration such as diffusion, mass transfer of the pollutants and biodegradation kinetics, which have been described in detail in the review conducted by Devinny and Ramesh [1].
Mohseni and Allen [2] have reported that the constituents of the biofilm have a significant impact on the solubility of the hydrophobic substrates in the biofilm. In their view, air/biofilm distribution coefficient, which accounts for the lipophilic characteristics of the biofilm, should be used, instead of the usual air/water distribution coefficient, for modeling the biofiltration of hydrophobic VOCs. Important parameters, mathematical modeling of biofilters looks quite challenging. Kiranmai et al. [3] have applied the differential evolution method for determining the biokinetics in their fixed-film reactor modeling problem.
Among these researches, the direct route that converts methane into high hydrocarbons in one step by the oxidative coupling reactions is more economically attractive and consequentially has been thoroughly studied [4,5]. The mathematical modeling of catalyst pellet in OCM process which is considered the heart of catalytic fixed bed reactor is the most important model used in describing the behavior of fixed bed reactor [6-17].
Many important physical phenomena on the engineering and science fields are frequently modeled by nonlinear differential equations.
Such equations are often difficult or impossible to solve analytically. Nevertheless, analytical approximate methods to obtain approximate solutions have gained importance in recent years [18]. There are several methods employed to find approximate solutions to nonlinear problems like homotopy perturbation method (HPM) [19,20], homotopy analysis method (HAM) [21,22], Adomian decomposition method (ADM) [23,24] and Picard’s iterative method [25,26] etc. Recently, Rajendran et al. solved the nonlinear differential equations in biosensor and biofuel cells using various analytical method [27-33].
However, to the best of our knowledge, till date there was no rigorous analytical expression of the concentrations for methane and carbon dioxide in a closed biofilter for all possible values of reactiondiffusion parameters have been reported [17]. The purpose of this communication is to derive approximate analytical expressions for the concentrations methane and carbon dioxide for all possible values of parameters using new approach of homotopy perturbation method.
Mathematical Formulation of the Boundary Value Problem
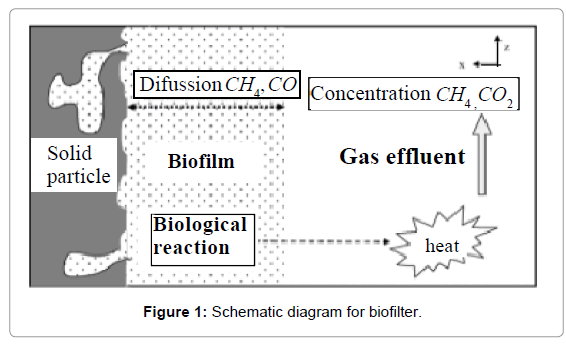
The general assumption of the mathematical models for methane bioelimination involving the closed biofilter is described [17]. Figure 1 denotes the phenomena occurring within the biofilter and considered in the present model. It contains the two components CH4 and CO2 through the gas phase and biofilm phase. During steady state operations, there is no accumulation of the pollutant, of the by-products or of the products within the biofilter. The general mass balances within the gas phase involve essentially three terms: an accumulation term, a convection term, and a mass exchange term through the interface of the gas phase with the biofilm. Within the biofilm phase, CH4 becomes biodegraded, forming CO2 among others. The mass balances equation of CH4 and CO2 gives as follows [17]:
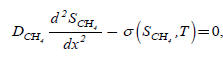 (1)
(1)
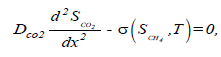 (2)
(2)
The boundary conditions are:
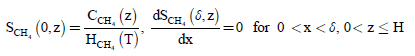 (3)
(3)
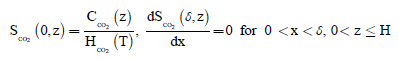 (4)
(4)
Where,
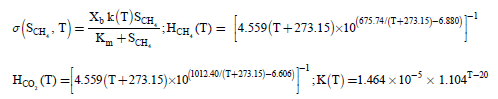 (5)
(5)
where SCH4 and SCO2 represents the concentration of methane and carbon dioxide in the biofilm phase. Xb and Km represents density of biomass in the biofilm and Monod constant. H(T) depends on the temperature T in °C, K(T) is the temperature dependent maximum substrate utilization rate and s is the consumption rate of CH4. The concentrations CH4 and CO2 within the gas phase described by the following equation:
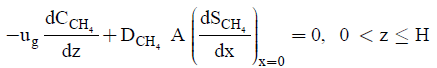 (6)
(6)
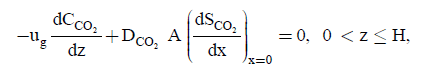 (7)
(7)
The initial conditions for the Eqn. (6) and (7) are:
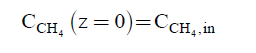 (8)
(8)
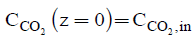 (9)
(9)
where CCH4 and CCO2 represents the concentration of methane and carbon dioxide in the gas phase. DCH4 and DCO2 represents the diffusion coefficient of methane and carbon dioxide in the biofilm respectively. ug and A represents the gas superficial velocity within the biofilter and specific surface of the packing material. The elimination capacity (EC) is:
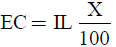 (10)
(10)
Where,
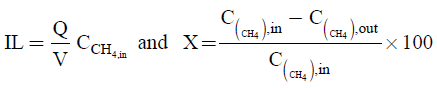 (11)
(11)
Analytical Expression of the Concentration of CH4 and CO2 in the Biofilm and Gas Phase Using New Homotopy Perturbation Approach
In recent days, new homotopy perturbation approach is often employed to solve several nonlinear problems in physics, chemistry and biochemical engineering. Furthermore, new homotopy perturbation approach is a simple, accurate and efficient method. The analytical solution of nonlinear equation is of great importance due to its wide application in scientific research. The new homotopy perturbation approach [34,35] is used to obtain the approximate analytical solution of non-linear reaction/diffusion Eqns. (1-2). Using the new homotopy perturbation approach (Appendix A), we can obtain the of the concentrations for methane and carbon dioxide in a closed biofilter as follows:
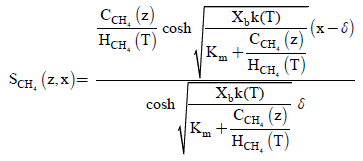 (12)
(12)
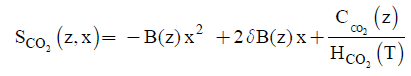 (13)
(13)
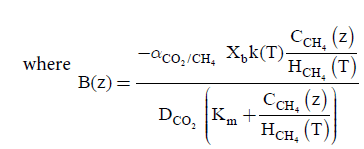 (14)
(14)
Also solving Eqns. (6-7) and (8-9) using the analytical method, we can obtain the concentration of CH4 and CO2 in the gas phase are as follows:
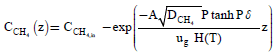 (15)
(15)
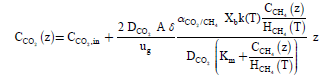 (16)
(16)
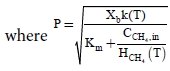 (17)
(17)
Using the Eqns. (10), (11), and (16) we can also obtain the elimination capacity.
Discussion
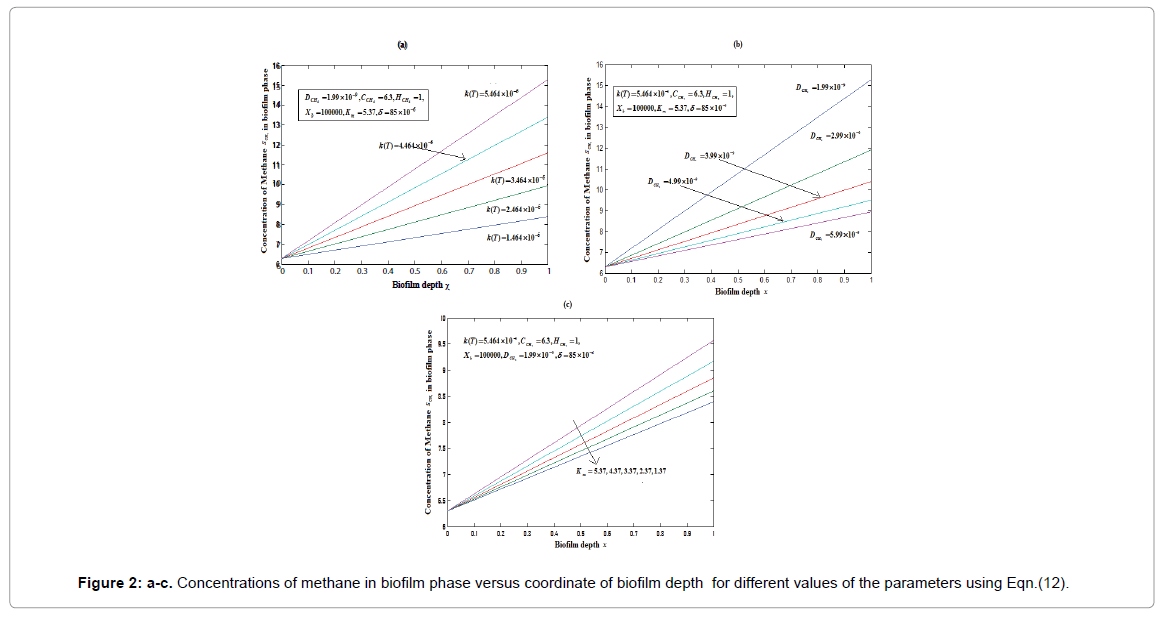
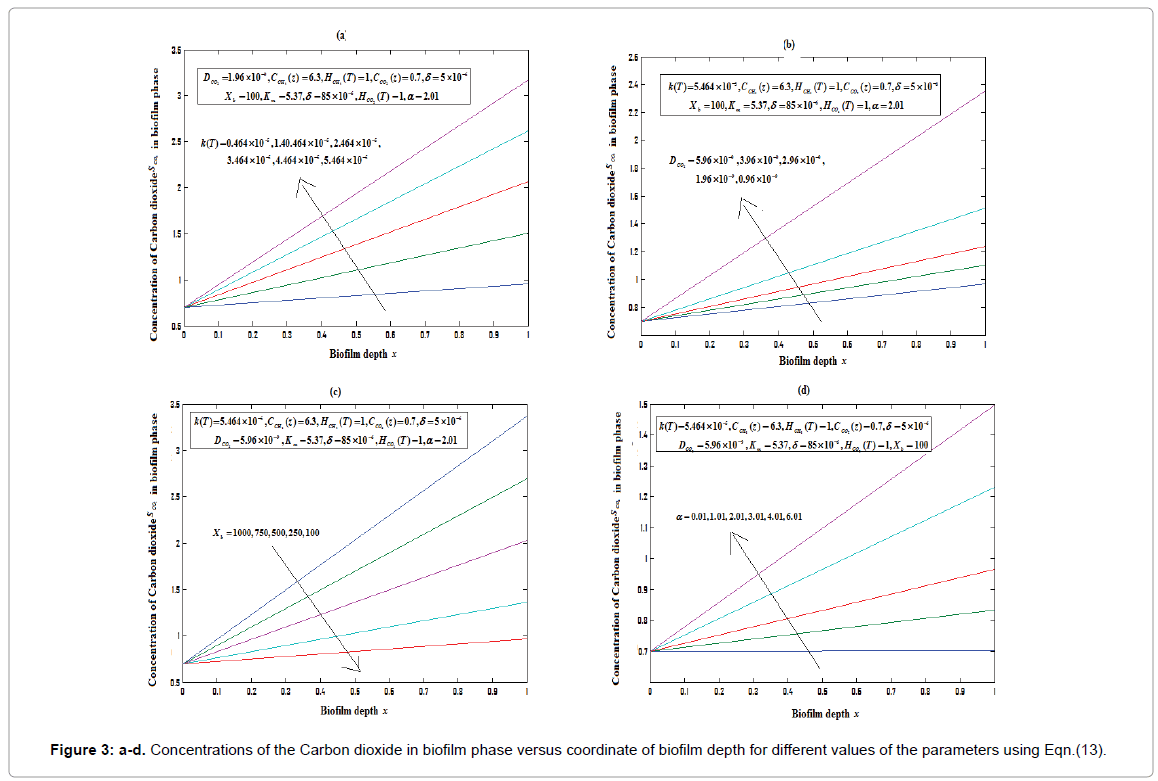
Equations (12) and (13) are the new and simple approximate analytical expressions of the concentrations of the methane and carbon dioxide in biofilm base calculated using homotopy perturbation method. The concentration profiles of methane versus height coordinate are expressed in Figures 2a-2c. From these Figures, it is inferred that the value of the concentration decreases when A and δ increase. The concentration of methane is increases when Monod constant Km is increases. The concentration profiles of carbon dioxide versus height coordinate are expressed in Figures 3a-3c. From these figures, it is observed that the value of the concentration of carbon dioxide decreases when Km increase. The concentration of carbon dioxide is increases when A and δ is increases (Table 1).
| Parameters | Values |
| A | 2750 m2/m3 |
| D | 0.015 m |
| DCH4 | 1.49 × 10-9 m2/s |
| DCO2 | 1.96 × 10-9 m2/s |
| Km | 5.37 g/m3 |
| Pendo | 7 g/m3/h |
| V | 0.0177 m3 |
| Xh | 100,000 g/m3 |
| Y | 0.34 g biomass/g CH4 |
| H | 1 m |
| CO2/CH4 | 2.01 g CO2/g CH4 |
| ε | 0.40 |
| δ | 85 × 10-6 m |
| µm | 4.98 × 10-6 S-1 |
| θ | 1.104 |
Table 1: Numerical value of parameters used in this work.
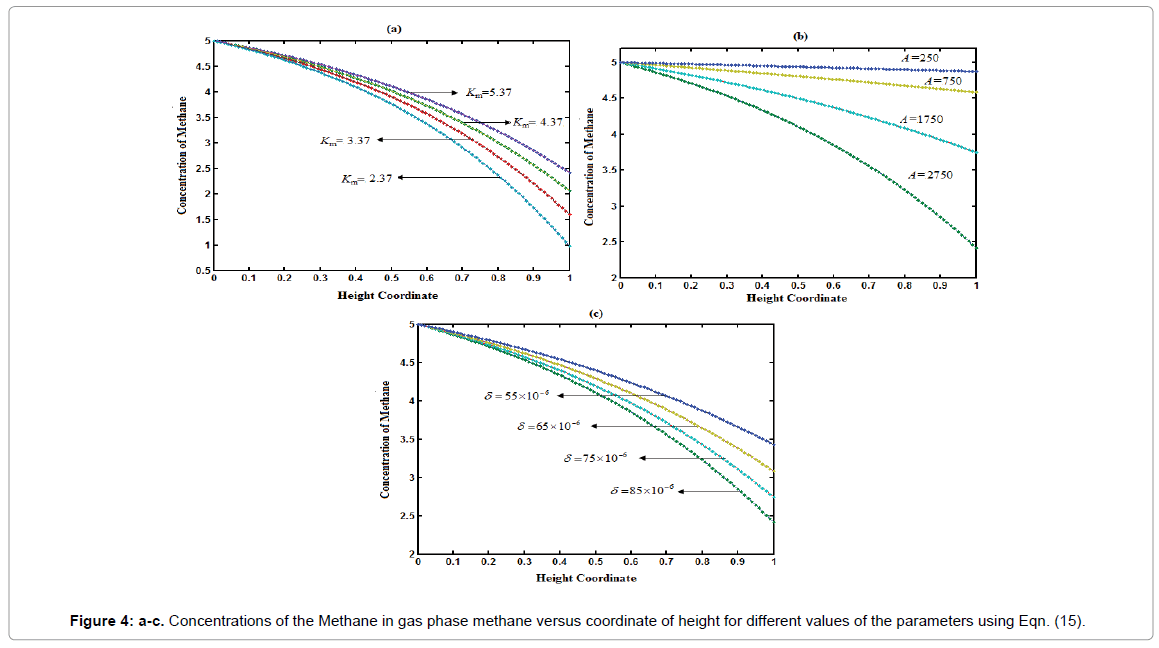
Equations (15) and (16) are represent the new and simple approximate analytical expressions of the concentrations of the methane and carbon dioxide in gas base. The concentration profiles of methane versus height coordinate are expressed in Figures 4a-4c. From these Figures, it is inferred that the value of the concentration of methane decreases when A and δ increase or Monod constant Km is decreases. Also, the concentrations of the methane in gas phase decreases slowly from its initial value for all values of parameters due to biodegradation of methane in gas phase.
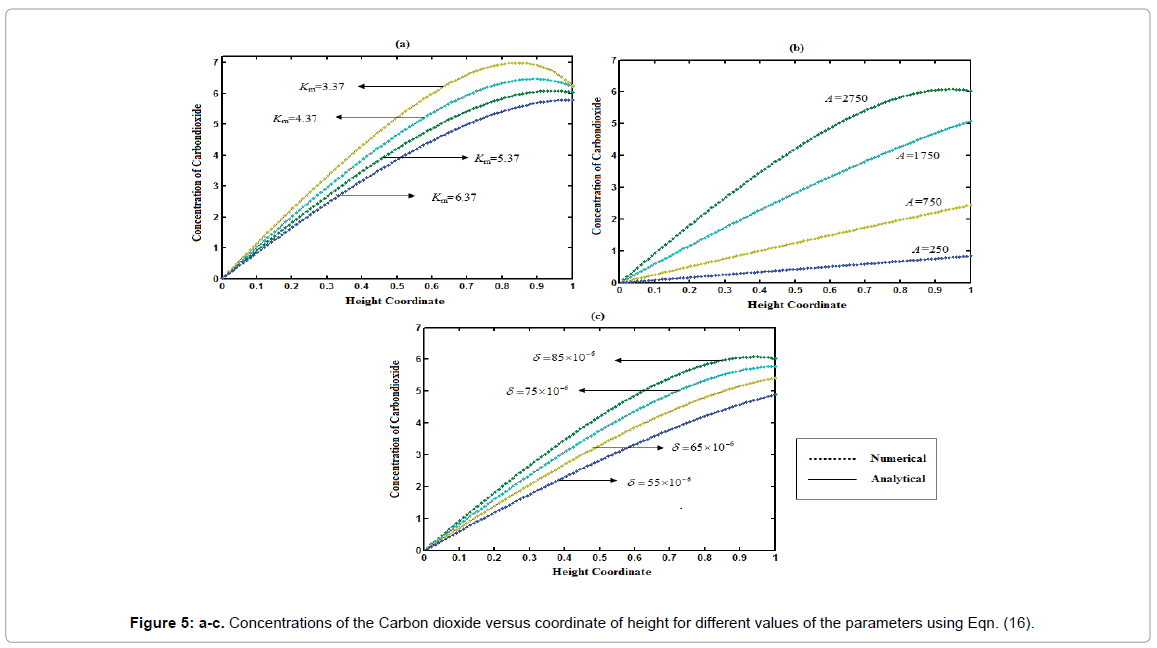
The concentration profiles of carbon dioxide versus height coordinate is represented in Figures 5a-5c. From these figures, it is observed that the value of the concentration of carbon dioxide increases when A and δ is increases or K decreases. The concentration of carbon dioxide is always increases due to production of carbon dioxide in gas phase. Our analytical results for the concentration of methane and carbon dioxide in gas phase is compared with simulation results (Matlab). Satisfactory agreement is noted.
Conclusion
In this paper, steady-state of solutions of a nonlinear reaction equations arising in elimination of methane has been studied. The theoretical model of biofilms Monod-type inhibition kinetics for the steady state condition is discussed. The nonlinear differential equation for methane and carbon dioxide has been solved analytically using the new homotopy perturbation method. The obtained results have a good agreement with those obtained using numerical methods. Theoretical results obtained in this paper can also be used to predict the response of biofilms.
References
- Devinny JS, Ramesh J (2005) A phenomenological review of biofilter models. Chemical Engineering Journal 113: 187-196.
- Mohseni M, Grant Allen D (2000) Biofiltration of mixtures of hydrophilic and hydrophobic volatile organic compounds. Chemical Engineering Science 55: 1545-1558.
- Kiranmai D, Jyothirmai A, Murty CVS (2005) Determination of kinetic parameters in fixed-film bio-reactors: an inverse problem approach. Biochemical Engineering Journal 23: 73-83.
- Keller GE, Bhasin MM (1982) Synthesis of ethylene via oxidative coupling of methane: I. Determination of active catalysts. Journal of Catalysis 73: 9-19.
- Krylov OV (1992) Free-radical reactions involved in C1-C3 hydrocarbons interaction with oxide catalysts. Catalysis Today 4: 481-486.
- Andrigo P, Bagatin R, Pagani G (1999) Fixed bed reactors. Catalysis Today 2: 3197-3221.
- Biazar J, Babolian E, Islam R (2004) Solution of the system of ordinary differential equations by Adomian decomposition method. Applied Mathematics and Computation 147: 713-719.
- Arriga S, Serrano MA, Barba de la Rosa AP (2012) Methanol vapor biofiltration coupled with continuous production of recombinant endochitinase Ech42 by Pichia Pastoris. Process Biochemistry 12: 2311-2316.
- Mohseni M, Grant Allen D (1999) Transient performance of biofilters treating mixtures of hydrophilic and hydrophobic volatile organic compounds. Journal of the Air & Waste Management Association 12: 1434-1441.
- Mohseni M, Allen DG, Nichols KM (1998) Biofiltration of alpha-pinene and its application to the treatment of pulp and paper air emissions. Tappi Journal 8: 205-211.
- Moradi O (2011) The Removal of Ions by Functionalized Carbon Nanotube: Equilibrium, Isotherms and Thermodynamic Studies. Chemical and Biochemical Engineering Quarterly 25: 229-240.
- Shareefdeen Z, Baltzi BC, Oh YS, Bartha R (1993) Biofiltration of methanol vapor. Biotechnology and Bioengineering 41: 512-524.
- Rene ER, Jin Y, Veiga MC, Kennes C (2009) Two-stage gas-phase bioreactor for the combined removal of hydrogen sulphide, methanol and α -pinene. Environmental Technology 91: 1261-1272.
- Premkumar R, Krishnamohan N (2010) Removal of methanol from waste gas using biofilteration. Journal of Applied Science Research 6: 1898-1907.
- Moradi O (2013) Adsorption behavior of basic red 46 by single-walled carbon nanotubes surfaces, Fullerenes. Nanotubesan and Carbon Nanostructures 4: 286-301.
- Elnashaie SSEH, Elshini SS (1996) Dynamic Modelling, Bifurcation and Chaotic Behaviour of Gas-solid Catalytic Reactors. Gordon and Breach Publishers, Amsterdam.
- Nikiemaa J, Payreb G, Hweita M (2009) A mathematical steady state model for methane bioelimination in a closed bioï¬lter. Chemical Engineering Journal 150: 418-425.
- Ellahi R, Zeeshan A (2011) Analytical solutions for nonlinear partial differential equations. Lambert Academic Publishing GmbH & Co. KG, Germany.
- He JH (1999) Homotopy perturbation technique. Computer Methods in Applied Mechanics and Engineering 178: 257-262.
- He JH (2005) Application of homotopy perturbation method to nonlinear wave equations. Chaos, Solitons and Fractals 26: 695-700.
- Liao SJ (1992) PhD Thesis. Shanghai Jiao Tong University, Shanghai, People’s Republic of China.
- Liao SJ (2012) Homotopy analysis method in nonlinear differential equations. Springer: Berlin, Germany.
- Adomian G (1991) A review of the decomposition method and some recent results for nonlinear equations. Computational Mathematics and Application 21: 101-127.
- Adomian G, Rach R (1993) Analytic solution of nonlinear boundary-value problems in several dimensions by decomposition. Journal of Mathematical Analysis and Applications 174: 118-137.
- Ramos J (2009) Picard’s iterative method for nonlinear advection-reaction- diffusion equations. Applied Mathematics and Computation 215: 1526-1536.
- Szinvelski CR, Vilhena MT, Carvalho JC, Degrazia GA (2006) Semi- analytical solution of asymptotic langevin equation by the Picard’s iterative method. Environmental Modeling and Software 21: 406-410.
- Anitha S, Rajendran L (2013) Reply to comments on analytical solution of amperometric enzymatic reactions based on Homotopy perturbation method by Ji-Huan He, Lu-Feng Mo. Electrochimica Acta 102: 474-476.
- Meena V, Indira K, Kumar S, Rajendran L (2014) A new mathematical model for effectiveness factors in biofilm under toxic conditions. Alexandria Engineering Journal 53: 917-928.
- Meena V, Praveen T, Rajendran L (2016) Mathematical modeling and analysis of the mole concentrations of ethanol, acetaldehyde and ethyl acetate inside the catalyst particle. Kinetics and Catalysis 57: 125-134.
- Meena V, Rajendran L (2016) Mathematical modeling of gas phase and bioï¬lm phase bioï¬lter performance. Egyptian Journal of Basic and Applied Sciences 3: 94-105.
- Meena V, Kirthiga OM, Rajendran L (2014) Analytical expression of concentration of substrate in biofilm reactor using Adomian decomposition method. Analytical & Bioanalytical Electro Chemistry 6: 713-732.
- Kirthiga OM, Rajendran L (2014) Analytical expressions of the concentrations of substrate, biomass, and ethanol for solid-state fermentation in biofuel production. Energy Technology 2: 574-578.
- Kirthiga OM, Rajendran L (2016) Analytical expression pertaining to the concentrations of biomass, sugar and ethanol production from wastewaters of the soft drink industries. International Journal of Modern Mathematical Sciences 4: 352-364.
- Biazar J, Eslami M (2011) A new homotopy perturbation method for solving systems of partial differential equations. Computers & Mathematics with Applications 62: 225-223.
- Rabbani M (2013) New homotopy perturbation method to solve nonlinear problems. Journal of Mathematics and Computer Science 7: 272-275.
Citation: Rani FMJ, Meena V, Rajendran L (2018) A New Approach of Solving the Nonlinear Equations in Biofiltration of Methane in a Closed Biofilter. J Anal Bioanal Tech 9: 405. DOI: 10.4172/2155-9872.1000405
Copyright: © 2018 Rani FMJ, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Open Access Journals
Article Tools
Article Usage
- Total views: 5210
- [From(publication date): 0-2018 - Dec 09, 2025]
- Breakdown by view type
- HTML page views: 4240
- PDF downloads: 970