A Parametric Study of the Effect of Building Distributions and Size on the Propagation of Sound in the Urban Environment

Whilst most of the work on noise in cities over the last five decades has been primarily concerned with the concept of noise as a nuisance or annoyance, there has recently been a move towards studies of responses to relatively low noise levels where environmental quality is the major consideration. There is considerable interest in the concept of soundscape and in the possible creation of acoustically pleasant areas as islands of relative calm in busy urban environments [1]. In this context, there may be no dominant source of noise, such as a nearby urban highway, but the area is characterized by a relatively low level of ambient noise arising from the combined effect of many distant sources. Until recently work on devising a prediction method for this situation was limited to an early attempt by Shaw and Olson to develop a theory of steady state urban noise for an homogeneous city [2]. This work involved theoretical modelling based upon a distribution of sources over an urban site. Comparison of predicted and measured levels was employed to obtain an estimate of the shielding effect of obstacles in the transmission path such as buildings. More recently work has been carried out on the propagation of sound for more complex situations than that along streets by Kang [3,4] who investigated the acoustical conditions in urban squares, and Thorsson, Ogren and Kropp [5] who investigated propagation between parallel street canyons.

This paper is concerned with an investigation of a more fundamental approach to that of Shaw and Olson for predicting the background noise levels in urban areas based upon modelling the propagation of sound through an urban location consisting of a distribution of small low rise buildings. What differentiates the propagation of sound through this type of urban fabric from street propagation, which has been extensively studied by many researchers [6-10] is the effect of occlusion by which individual buildings shield other buildings in the course of the propagation process. This situation also differs from the configurations referred to in ISO 9613-2 which concern groups of buildings in close proximity to a major noise source such as a highway [11]. The net effect at a point deep in the urban fabric of noise arising from the operation of multiple distant sources can be expected to be a function of the building density in this area. Early work in this area was carried out by Leschnik [12] and Kuttruff [13] who treated buildings as point scatterers of sound with a finite capture cross section. This approach is suited to a low density distribution of small buildings. However, in this paper the concern relates to the relatively dense concentrations of low rise and medium sized buildings that characterize the urban residential areas of many cities.

The underlying physics behind sound propagation through an urban area is very complicated as involves specular and diffuse reflections, partial absorption, diffraction and scattering. The urban fabric includes a huge number of facades, each facade being composed of various materials and with different geometrical configurations [6,14]. In this paper a simplified model will be described in which the building facades of the city are replaced by a network of nodes which act as secondary sources, assigning sound energy to other facades. The facades are assumed to be totally Lambertian diffuse surfaces, radiating reflected energy to other facades. Although the reflection characteristics of building facades are generally considered to be partially specular and partially diffusely reflecting, recent work has established that there is a rapid transfer of energy from the specular reflected field to the diffusely reflected field as the order of reflection increases [13].

The use of this approach for modelling the propagation of sound in urban areas can be justified as the noise sources found in such areas tend to be broadband in nature and the sound field at any point will be the result of multiple reflections and hence interference effects are not significant. If values of parameters such as facade absorption coefficient are employed then values corresponding to that applicable to an A weighted traffic noise spectrum can be employed. This approach is the basis of the radiosity [14] method which has been extensively employed by Kang [3,4,9] in investigations of urban noise propagation but over relatively small areas.

There are three possible approaches to the investigation of sound propagation through the urban fabric. The first is by means of field studies in real locations, however, this is not practical for studying propagation over a wide area where numerous independent sources are in operation and the resulting ambient noise levels are relatively high. The second is to employ scale models, as used for example by Horoshenkov, Hothersall and Mercy [15] to study noise propagation in a street canyon. However, this is again not practical if noise propagation over a large area is to be studied as the large scale factor that would be required would mean working at very high frequencies with problems of instrumentation and air absorption. The final approach is computer modelling which has been the approach favoured by many investigators in modelling aspects of urban noise propagation [6].

In developing the model the main problem that had to be overcome was to devise a technique for dealing with the complexity of the propagation path and in particular the occluding effect that occurs with propagation through a complex array of buildings.

As mentioned above, there is considerable difficulty in modelling the actual complexity of an array of building facades and a simplified approach is necessary. The computer model in the study considers the urban fabric as being composed of a regular arrangement of simple rectangular blocks with façades that are diffusively reflecting rectangular planes. The site is assumed to be perfectly flat; hence it is a flat city model as defined by Thorssen et al. [15]. The computer program is employed to generate a Cartesian co-ordinate system representation of the building layout, with all streets and building faces aligned in either the X or Y direction.

Non straight streets, tapering streets, non-perpendicular intersections, etc. are ignored in this stage of the study, for simplicity and for the sake of reducing computing time. The building blocks are separated by corridors or streets, the streets aligned in the X direction are termed longitudinal streets and those aligned in the Y direction are termed lateral streets.

Parameters that might be expected to affect the propagation of sound through a distributed array of buildings include the density of the building fabric, the ground floor dimensions of the building, the building height, and facade absorption characteristics. In order to carry out a parametric investigation of the effect of these parameters a large number of site models need to be constructed. For this study a computer model was developed which utilised the above parameters as inputs and enabled the rapid construction and testing of a range of different models.

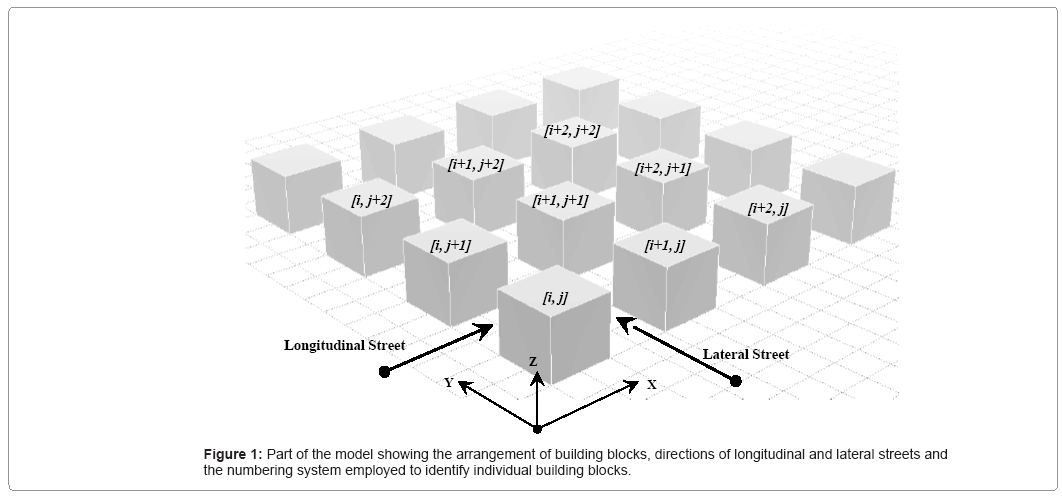
The development of the computer model required a number of simplifying assumptions. A rectangular site plan of Length L and width W was assumed and a Cartesian co-ordinate system was employed with the length direction aligned with the X axis and the width dimension aligned with the Y axis. Buildings, represented in the form of simple rectangular blocks, were arranged nx rows and ny columns as illustrated in Figure 1.

Figure 1: Part of the model showing the arrangement of building blocks, directions of longitudinal and lateral streets and the numbering system employed to identify individual building blocks.

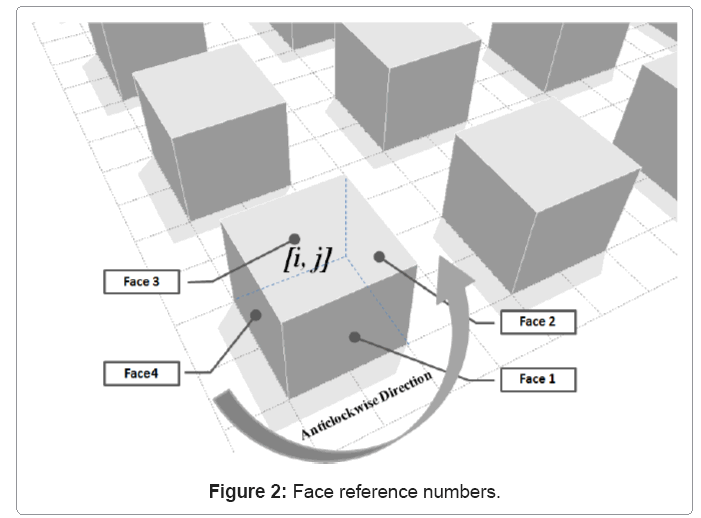
The location of a particular building block inside the whole building pattern is defined by two variables, the number of columns of blocks, i, and the number of rows, j, as shown in Figure 1. The perpendicular faces of a block are identified by a further subscript which relates to the alignment of the faces as shown in Figure 2.

Figure 2: Face reference numbers.

The co-ordinates of the centres of the buildings are given by:

x_i=i L/(n_X+1)

y_j=jW/(n_y+1)

The second simplifying assumption was to assume an equal spacing, d, of the building blocks. From this the following expressions for the ground floor dimensions of the blocks, LB and WB,could be determined:

L_B= L/n_X–d

W_B=W/n_y–d

The value of d is a function of the building fabric density, ρB, and is given by the following expression:

d=(n_XW+n_YL–[(n_XW+n_YL)2–4 n_X ²n_YL²W(-ρB,)]^0.5)/2n_Xn_Y

The dimensions of the building ground floor dimensions are thus simply related to the building density and number of rows and columns of buildings specified by the user and thus the input variables are kept to a minimum whilst allowing great flexibility in designing the building layout. In the present model all buildings are assumed to be all of the same height.

The effect of different building heights on sound propagation remains an area for further study.

Additional parameters required are the number of field points required along the streets and the height of these points plus to coordinates and power of the sound source. With these input variables it is possible to generate different configurations of rectangular shaped building layouts, with different building heights and plot area density.

In this study an arrangement of square buildings on a square site was assumed, thus L=W and nX=nYt. For this configuration it is possible to write the following simple expression relating the block ground floor dimensions, LB, to the building density and number of rows or columns:

L_B=L ρ^0.5/(nX)

The sound propagation mechanism assumed is based upon the interchange of energy between faces. This is a function of the positions of the faces relative to each other and their surface area, and hence the position of the building edges points and the position of the sources. The computer program thus calculates the Cartesian co-ordinates of all the edge points of the buildings.

The sound propagation mechanism considered is based upon the interchange of energy between facades arising from diffuse reflections from the facades. In the model, the building facades of the city are replaced by a network of nodes which act as secondary sources assigning, energy to other facades. The propagation process proceeds until steady state conditions are achieved. The distribution of sound energy starts with the energy assigned directly from a source to those facades which are not occluded by any obstructing objects present in the transmission path. It then continues with the interchange of energy, between the illuminated areas of those facades and the facades of all other the building blocks that are not completely occluded.

The main stages in the development of a model for sound propagation through the urban fabric are thus:

1. The initial distribution of sound energy (or “illumination”) from a source to building facades;

2. The re-distribution of energy from the “illuminated” facades to other facades;

3. The re-distribution of energy from the “illuminated” facades to locations, termed field points, in the street channels.

In the course of the propagation process, stages 2 and 3 will be repeated according to the different order of reflections. At each order of reflection the illuminated areas of the facades can be considered to be secondary sources. However, the situation is complicated by the fact that different faces will be illuminated, either totally or partially, at different orders of reflection in a similar way to that for the initial distribution of sound from a point source as illustrated in Figure 3. The white areas shown in Figure 3 illustrate those parts of the facades that are illuminated by the sound from the source. It can be seen that the distribution and characteristics of the secondary sources, both their positions and effective areas, will vary with each order of reflection.

Figure 3: Assignment of sound energy building surfaces–white areas indicate parts of facades illuminated by sound from a point source.

Thus, two problems have to be overcome in developing the model. The first is to devise a method for the treatment of occlusion in relation to the initial distribution of sound from a specified point source to visible facades, the distribution of sound from illuminated facades to other facades and from illuminated facades to specified field points. The second is to devise an efficient method of treating the facade to facade radiation of sound throughout the urban fabric which can deal with the varying nature of the secondary sources.

Once the geometrical environment is constructed, the next step is to distribute the sound energy of the source to those facades which are within the scope of the source and this means that occlusion is to be taken into account, hence these two problems will be considered together.

The treatment of occlusion

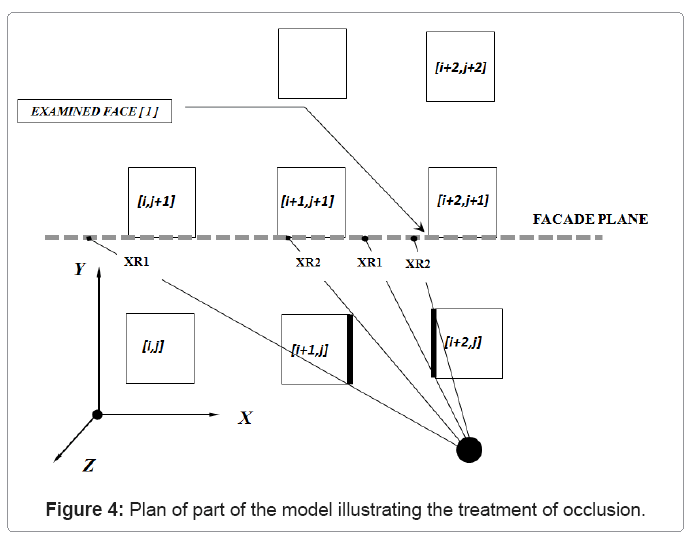
The effect of occlusion is treated by first identifying those facades that cannot be illuminated by the source. For example, for the arrangement shown in Figure 4, if the X co-ordinate of the source position is less than that of the X co-ordinate corresponding to that of face 2 of a row of building blocks then these faces cannot be illuminated. However, if the X co-ordinate of the source position is greater than that of the X co-ordinate corresponding to that of face 4 of a row of building blocks then these faces cannot be illuminated. Similarly, if the Y coordinate of the source position is less than that of the Y co-ordinate corresponding to that of face 2 of a row of building blocks then these faces cannot be illuminated whilst if the Y coordinate of the source position is greater than that of the Y co-ordinate corresponding to that of face 4 of a row of building blocks then these faces cannot be illuminated. As a result of this process, those facades not involved in the interaction process can be filtered out of the calculation procedure.

Figure 4: Plan of part of the model illustrating the treatment of occlusion.

Having identified those planes that can potentially be illuminated, it is then necessary to establish their degree of occlusion by calculating the occluded ranges on each facade line as illustrated in Figure 4. These ranges are then compared with the vertex co-ordinates of the facades lying along this line from which it can be established if a particular facade is totally occluded, partially occluded or not occluded.

For the case presented in Figure 4, facade 1 of block [i+1,j+1] can be seen to be partiallyoccluded whilst facade 1 of block [i,j+1] is totally occluded. The same procedure can be applied for facades lying along the Y direction and for facade lines corresponding to situations where there are more than one row of building blocks between the source and the tested facades.

The assignment of first order energy

As stated above, in developing the model, diffuse reflection of sound from the facades is assumed. Kang has demonstrated that the technique of radiosity is suitable for modeling sound propagation due to diffuse reflections [6]. In radiosity treatment, the distribution of energy from a point source to a receiving surface is treated by means of a configuration factor. This relates the total sound power of a source to the average energy received over the surface. In the context of the initial distribution of energy from the source to the building faces, the configuration factor for a particular illuminated facade relates to the area that is illuminated. Each face that is either not occluded or only partially occluded is identified as described in the previous section. In the case of partially occluded faces, the extent of the illuminated region of that face is established. For example, in Figure 4 it can be seen that the examined face of middle block is partially occluded such that the X co-ordinates of the illuminated region range from XR2 to that of the right hand corner of this block.

With the initial distribution of sound energy established, the next stage is to begin the process of exchanging this energy between all the faces in the model. A form factor is employed in conventional radiosity to relate the excitance of a diffuse area emitter to the average sound energy it produces over a receiving area. The use of these parameters contributes to the efficiency of any computational process where multiple orders of reflection are being considered, such as in a street canyon, if all the surface areas contribute to the resultant sound field and if their effective areas remain constant for all orders of reflection.

However, as can be seen from Figure 3, when dealing with sound propagation through an array of building blocks, these conditions will not apply due to the effect of occlusion. At any given order of reflection, some surfaces will be fully occluded, some surfaces will be partially occluded and some surfaces will not be occluded. Thus, there will not be a fixed array of faces, each of a constant area and each reacting with all other facades during each order of reflection. Hence there is a need to develop a technique which takes into account the complexity of this situation.

In the model described in this paper, two strategies are employed to deal with the problem.

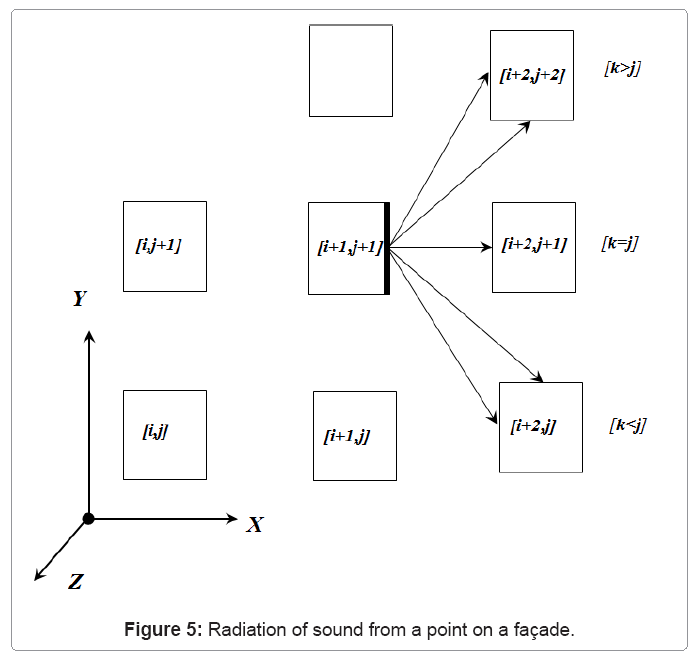
First, at each stage in the process (i.e. each order of reflection) each potentially receiving facade is tested to check if it is occluded by intervening blocks using a similar procedure to that developed for determining occlusion for the initial sound distribution from the point source. Secondly, radiation from individual facades is modelled by means of a hemispherical radiation from a point centred on the illuminated area of this facade, as illustrated in Figure 5, and with a sound power determined by the energy incident on that illuminated area. Thus at each order of reflection new arrays of point sources are generated corresponding to the face areas illuminated due to radiation from other faces. The energy arriving at a receiving face is determined by the solid angle subtended by that face relative to the location of the assumed point source.

Figure 5: Radiation of sound from a point on a façade.

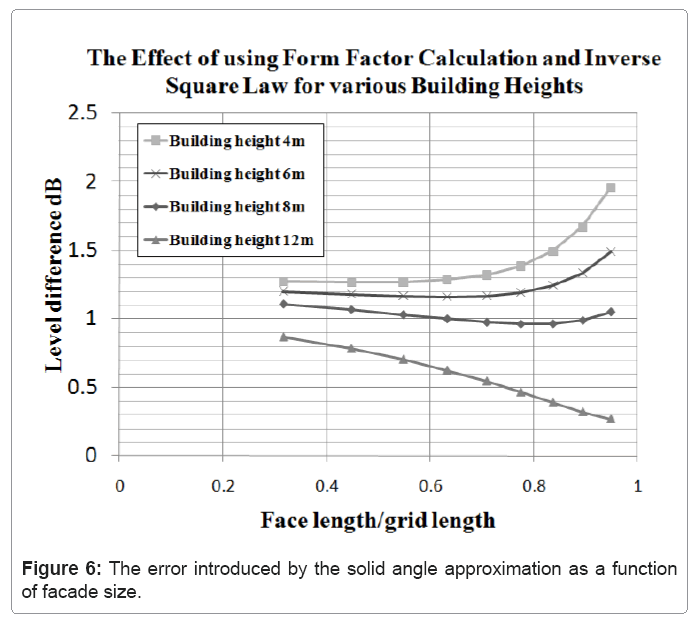
The effect of this simplifying assumption was tested for the worst case scenario that of two large rectangular faces separated by a small distance, by comparison with calculations made using accurate form factors and the radiosity method. By variation of building density (face length to grid length ratio) and the building height, the difference between obtained by the two methods could be investigated for different facade areas, facade aspect ratios and separations and the results are shown in Figure 6. It can be seen that apart from the highest ratios of face length to grid length, which correspond to impractically high building densities, the error is typically of the order of 1dB with the solid angle approximation tending to underestimate the levels. This level of inaccuracy was judged acceptable in view of the large gains in computational efficiency.

Figure 6: The error introduced by the solid angle approximation as a function of facade size.

The objective of the model is to investigate the sound level in the external environment as afunction of building density and building size. A number of field points can be specified alongany particular street with a specified height. Field point height variation is not possible in thisstage but may be included in further development of the program, thus all the field points areat equal height.

The first stage in determining the total energy arriving at a given field point is to test eachfacade for occlusion. This is essentially the same procedure as employed for determining theocclusion effect and initial distribution of sound energy from the point source. With the all thefacades that can radiate energy to a field point identified, it is then possible to calculate aconfiguration factor which relates the average energy over the visible portion of the face tothe sound energy received at a point.

The total amount of energy that arrives at each field point from the non-occluded and partially occluded faces for all orders of reflection considered is summed. In order to allow post processing of the data using different arrays of field points, and to reduce the complexity of the calculation, the energy arriving at each facade was summed over all orders of reflection. In calculating sound radiation to a field point from a partially occluded facade, the energy radiated was assumed to be equal to the total energy collected on that façade over all orders of reflection, multiplied by the ratio of visible face area to total face area.

The objective of this work is to study the effect of the building density and building size on the propagation of sound over a large distance through the urban fabric. It differs from work on street propagation where the objective is to study the channelling effect of a street, normally lined by a continuous arrangement of buildings and where propagation is normally considered over a relatively short distance.

The first configuration investigated was of a site measuring 1,000 m × 1,000 m with a building density of 50% and building height of 9 m. The building block dimensions were adjusted to be approximately 20 m × 20 m by inputting a value of 34 for the number of rows or columns into Equation 6. The values of these parameters were judged to be appropriate for the modeled urban form which was considered to be largely residential in nature. A façade absorption coefficient of 0.1 was assumed, in line with that suggested by most other researchers in this area [7], and a source was located at the centre of the site with an acoustic power of 1 watt. Field points were located at each street intersection.

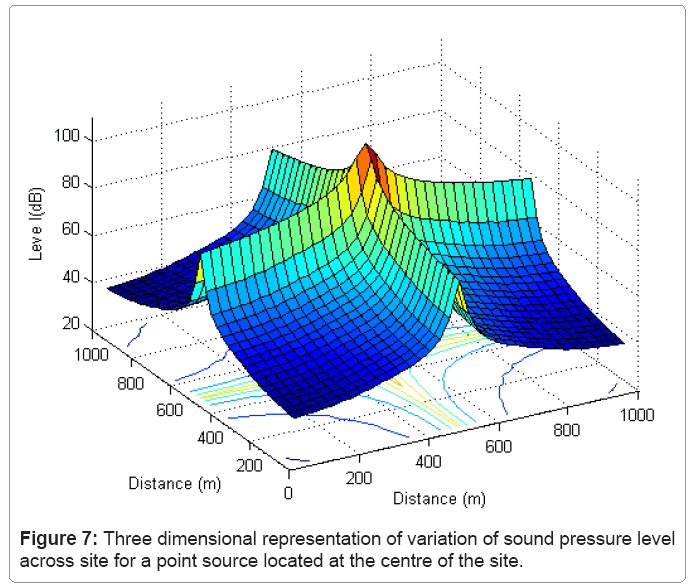
Figure 7 shows a three dimensional plot of the levels obtained. From examination of Figure 7 the effect of a street on the channelling of sound from the source can be seen very clearly.

Figure 7: Three dimensional representation of variation of sound pressure level across site for a point source located at the centre of the site.

The location of the source, at the centre of the site, means that there is a direct path from the source to all facades lining the two central streets and this, coupled with the relatively efficient energy exchange between parallel facades on either side of a street, gives rise to the distinctive ridges that can be seen on Figure 7.

Another feature that is visible on Figure 7 is the apparent sharp drop in level at the site boundaries. This is an artefact resulting from the calculation method. As sound propagates outwards from the position of the source, each newly illuminated façade acts as a secondary source and it energy is re-distributed. The effect is that facades close to the source will receive illumination from many other facades a number of times (corresponding to a large number of orders of reflection) whilst faces very far from the source will be illuminated a relatively few times.

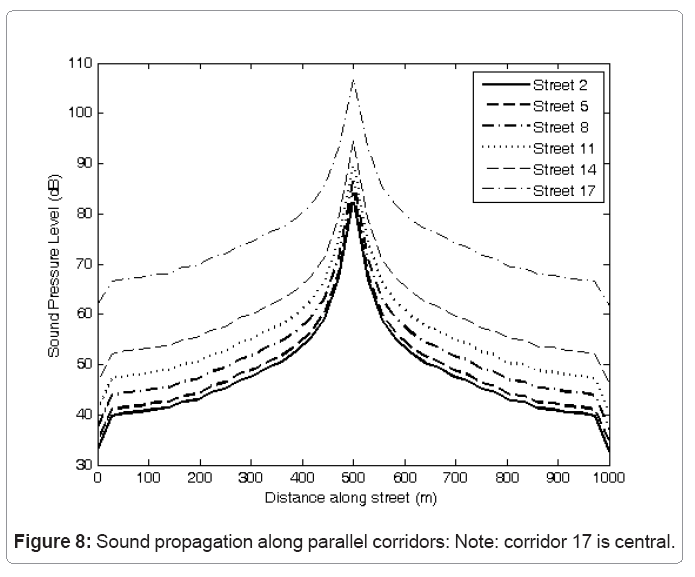
Figure 8 shows the variation of sound pressure level along a number of parallel streets. The streets are numbered from the site boundary and thus street 17 corresponds to that at the site centre. It can be seen that the sound pressure level decay characteristics are similar for all streets but are lower for those streets furthest from the centre line. As the distance from the centre line increases the differences between the decay characteristics of neighbouring corridors decreases.

The propagation characteristics shown in Figure 7 and Figure 8 are determined by the form of the building layout that has been modelled with the regular arrangement of buildings and source located between the facades lining two streets which results in the street channeling effect. The propagation characteristics across a less regular distribution of buildings can be investigated by considering a line of field points not aligned with the street structure and in this way the effect of varying different parameters can be investigated.

Figure 8: Sound propagation along parallel corridors: Note: corridor 17 is central.

Figure 9 shows the propagation characteristics along a site diagonal for four different site configurations. These sites each measured 500 m×500 m and the source was located at the origin (the bottom left hand corner of the site). This position was selected so that there would be no line of sight between the source and field points located on a site diagonal which passed through the origin. Thus, all data collocate would relate to sound reflected via the facades. The reduced site dimensions were employed to avoid the redundancy observed when considering the source at the central location of the 1,000 m×1,000 m site.

Figure 9: Effect of building density on sound propagation across the urban fabric.

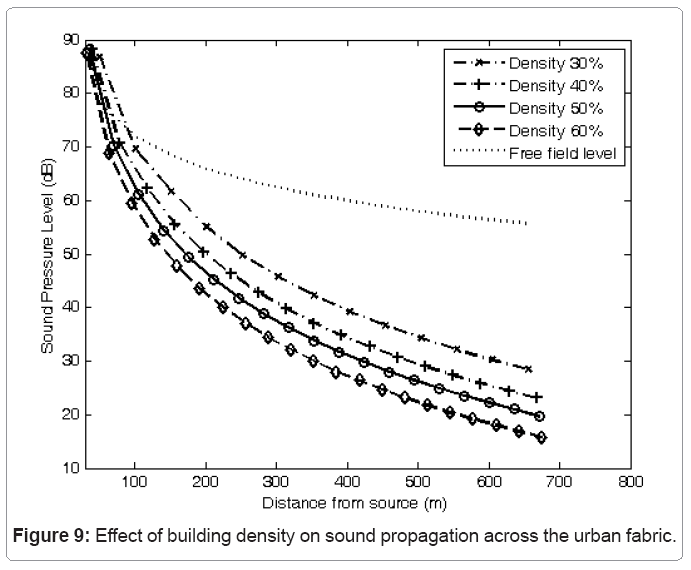
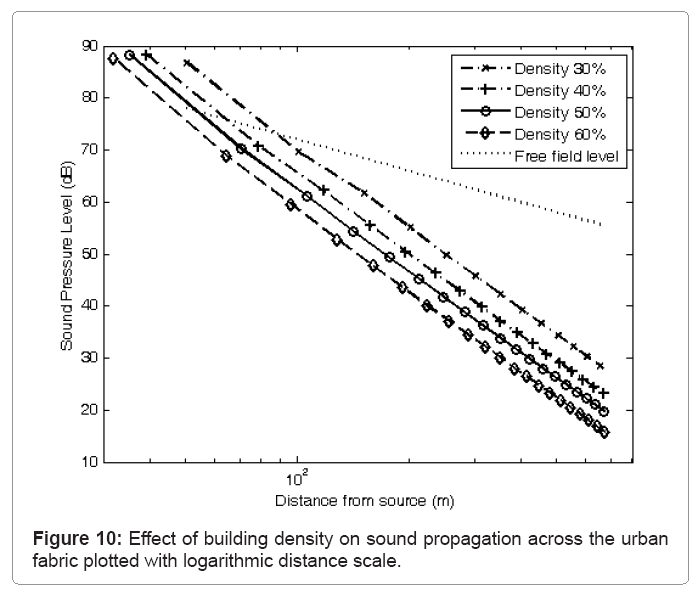
This part of the work involved an investigation of the effect of building density on the noise propagation characteristics of urban areas. Building densities of 30, 40, 50 and 60% were examined whilst keeping the block area dimensions approximately 20 m×20 m and the block height at 9m. It can be seen from Figure 9 that there is a systematic decrease in the far field noise levels as the building density increases with a difference between the 30% density and 60% density approaching 10 dB at 600 m. This is probably due to the greater occluding effect resulting from the increased building density.

Also shown on Figure 9 is the sound pressure level variation over distance for a source of acoustic power 1 watt located in the ground plane and assuming hemispherical radiation. It can be seen that the effect of the buildings is to enhance the noise level above that from the source in free field conditions for points relatively close to the source location due to strong reflections from the closest facades. However, as the source receiver distance increases the effect of occlusion becomes greater resulting in the noise level arising from sound propagation through the urban fabric becoming less than that for unobstructed free field propagation.

Figure 10 shows the same data but plotted with a logarithmic scale for the distance. It can be seen that whilst the curves for each configuration are similar but have different sound pressure levels at any specified distance from the source, the sound attenuation rates for each density are linear on this plot and are virtually identical at approximately 52dB per decade. The difference in levels at a particular location can be attributed to the near field effect of local occlusion in the vicinity of the source which will be greater for the cases with higher building density. The similar attenuation rates suggest that after the initial occlusion effect has determined the amount of sound energy that progresses to the far field, the effect of occlusion for a higher building density is compensated for by reflections from the increased number of facades.

Figure 10: Effect of building density on sound propagation across the urban fabric plotted with logarithmic distance scale.

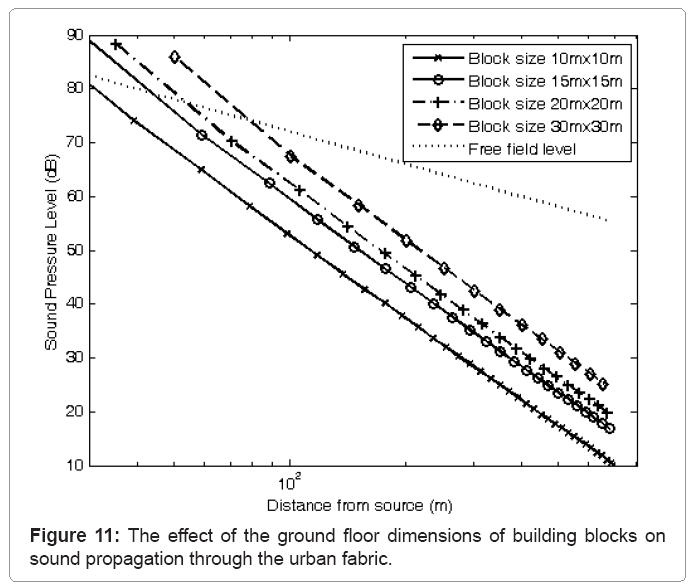
In the previous examples a building a block area of dimensions of 20 m x 20 m was assumed along with a building height of 9 m which were judged to be appropriate for the modeled urban form which was considered to be largely residential in nature. Figure 11 shows the effect on sound propagation of variations of floor area dimensions from 10 m x 10 m to 30 m x 30 m for a fixed building density of 50% and building height of 9 m. It can be seen that the curves for each configuration are similar but have different sound pressure levels at any specified distance from the source. The sound attenuation rates for each configuration are again linear and are virtually identical at approximately 52dB per decade. The far field noise level increases with increasing floor area dimensions. This may be due to the fact that decreasing the block areas whilst maintaining the building density requires a greater number of building blocks with a resulting increase in occlusion.

Figure 11: The effect of the ground floor dimensions of building blocks on sound propagation through the urban fabric.

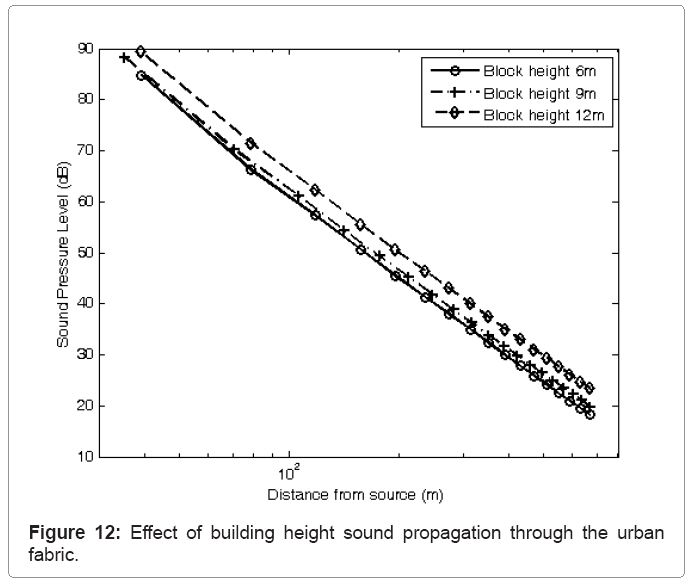
Figure 12 shows the effect on sound propagation through the urban fabric of variations in building heights from 6 m to 12 m on sound propagation. In this study a building density of 50% was assumed with block area dimensions of 20 m×20 m. It can be seen that the curves for each configuration are again similar but have different sound pressure levels at any specified distance from the source. The sound attenuation rates for each configuration are again linear and are virtually identical at approximately 52 dB per decade. The noise level at any given distance is slightly larger for the highest buildings considered. This is due to the larger facades resulting in more effective façade to façade energy interchange with less energy being scattered up to the sky.

Figure 12: Effect of building height sound propagation through the urban fabric.

Sound propagation through an urban fabric consisting of an array of medium sized buildings has been investigated, assuming that building facades give rise to diffuse reflections.

Diffusion is introduced to take account of the complex nature of sound propagation through the urban fabric, such as multiple reflection and diffraction. The geometrical complexity of the urban scene, and the intense nature of the radiosity calculations, suggested the need to devise an alternative simple investigative tool. The method adopted was to calculate the energy exchange between facades by means of solid angles, assuming hemispherical propagation from a point at the centre of a facade. Thus, the energy exchange between faces is replaced by arrays of point sources located at the centre of each face. Results obtained from this approach were compared with those obtained from applying the radiosity theory and proved to be comparable.

The model was developed using Fortran, and has been used to investigate the effect of different building parameters on the propagation of sound through the urban fabric. For the very regular street configuration employed in the model, it was found that there was a strong channelling effect when the source was located between the facades lining a street. This channelling effect was observed both for sound propagation along the street containing the source and also along parallel streets.

The propagation of sound across a more irregular fabric configuration as a function of building density, building plan dimensions and building height was investigated. It was found that the sound attenuation rates for each configuration are linear and virtually identical at approximately 52 dB per decade. However, for each configuration there are differences in levels at a particular location that can be attributed to the near field effect of local occlusion in the vicinity of the source. The similar attenuation rates suggest that after the initial occlusion effect has determined the amount of sound energy that progresses to the far field, the effect of occlusion is compensated for by reflections from the facades. It should be noted that these findings relate to the configurations examined where the building sizes were not large.

The model has been demonstrated capable of facilitating a detailed investigation of the effect of different parameters on sound propagation through the urban fabric. Further development of the model could involve including the effect of atmospheric absorption.

Future investigations will include the effect on urban noise propagation of buildings with different aspect ratios and variations in street widths over the site area. Finally, the effect of noise due to a distribution of local sources within the site plus a dominant source external to the site such as a busy urban highway will be investigated with a view to developing a model for the prediction of the ambient noise levels in urban locations. Such a model could be valuable in devising acoustic strategies for improving aural comfort in busy cities.