Research Article Open Access
Acoustic Logging Methods in Fractured and Porous Formations
Sudad H Al*
University of Hayat, Erbil, Iraq
- *Corresponding Author:
- Sudad H Al
Professor
University of Hayat
Erbil, Iraq
Tel: + 964 750 977 1896
E-mail: drsudad@gmail.com
Received Date: May 04, 2017; Accepted Date: May 11, 2017; Published Date: May 19, 2017
Citation: SH (2017) Acoustic Logging Methods in Fractured and Porous Formations. Oil Gas Res 3: 139. doi: 10.4172/2472-0518.1000139
Copyright: © 2017 Al SH. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Oil & Gas Research
Abstract
Formation fractures have significance importance in the rocks permeability of oil and gas reservoirs. In real conditions, the opening of vertical fractures exceeds the opening of horizontal fractures and the permeability of reservoirs in conditions of horizontal wells is higher than in vertical conditions. For the sonic log longitudinal waves, unlike the transverse waves, the attenuation rate strongly depends on the wave path direction. It is shown that the mechanism of attenuation of sound waves in porous rocks is represented by the scattering of “soft” microheterogeneous inclusions. For reservoir rocks with a porosity coefficient (φ) of (10-20)%, the attenuation decrement is several times higher than the decrement of the other mechanisms.
Keywords
Porosity; Fractures; Pores; Acoustic logging; Attenuation decrement; Permeability; Longitudinal waves; Transvers waves
Introduction
The fractures and pores of rocks, in many ways, determine the hydrocarbon content of oil and gas fields. However, measuring the porosity and permeability of reservoir rocks, using geophysical methods is a difficult task. In the solution of the permeability problem, a significant progress has now been made in connection with the invention of the method based on monitoring the penetration of drilling mud into the near-wellbore space [1,2]. The effectiveness of this method depends on the completeness of the information about the geometry and degree of the opening of rocks fractures, which play the role of channels in the process of fluid flow. Naturally, the main interest here is those fractures that are oriented in a direction orthogonal to the borehole axis. The study of fractures in rocks is devoted to extensive geological and geophysical literature [3,4]. However, unfortunately, there are very few publications devoted to the method of studying the direction of the surface of fractures and the degree of their unfolding. Therefore, in dealing with this problem, one can use only the most general provisions of geology and mechanics:
1) Fractures at the stage of formation under the action of tectonic processes have a complex form and, more often, an arbitrary spatial orientation of the surface;
2) In the further evolution of rocks, the characteristics of fractures opening become dependent on their direction relative to the compressive pressure (usually vertical). In view of the fact that vertical compression is stronger than horizontal compression, there is a greater “collapse” of horizontal fractures, which leads to their predominance over vertical ones. Therefore, from the point of view of higher oil recovery, horizontal wells have advantages over vertical ones, since the fractures surrounding them are orthogonal to the well axis.
Experiment of Physical Modelling to Study the Effect of Structures with Directional Fractures on the Field of Seismic Waves
A visual representation of the possibilities of acoustic methods for revealing geological structures cut by a system of parallel fractures is given by a physical modelling experiment performed on sheet models [5]. In these models the enclosing medium was imitated by a thin aluminium sheet and the fractures in crosscuts of this sheet. During the experiment, the probing base turned relative to the normal to the direction of fractures in a circle from angle ?=-π/2 (coinciding with the direction of fractures) to the angle ?=π/2 (to the opposite direction of the fractures). The wave fields of the longitudinal and transverse waves are shown in Figure 1. The first path on the left corresponds to the standard (solid) object in which fractures are absent. A comparison with the standard allows us to visually see the influence of fractures, namely: reducing the speed - signal delay and an increase in the attenuation -reduction of amplitude and increase of the visible period (decrease in frequency band) of the probe pulse (Figure 1). The influence of fractures on the physics of propagation of longitudinal waves is quite expected: When the beam (ray) is directed orthogonally to the surface of the fractures, the velocity becomes minimal, and the attenuation is maximal. As for the effect of the fractures on the physics of propagation of transverse waves, the result of the experiment here is unexpected. Indeed, the change in the direction of probing with respect to the direction of the fractures practically does not affect either the propagation velocity or the attenuation of the probing wave. Therefore, information about the presence of directional fractures in the probed medium actually carries only longitudinal waves.
Study of Fractures and Pores of a Probed Medium by Standard Acoustic Logging Probes
Typical for industrial practice, the design of the sonic logging tool contains a magnetostrictive source that located at some distance from it two geophones (piezoelectric receivers of sound signals). The distance between the source and the nearest geophone is most often selected in L1=1-2 m. The distance between the near and far geophones is L2=0.4 m. In the industrial environments, the acoustic parameters of the probed medium are usually determined on the basis of the spatial interval of L2. The speed of sound, typically measured in the simplest way: as the ratio of the base L2 to the interval time of wave propagation t2 - t1:
V=L2/(t2 - t1)
Decrement of attenuation could happen by decreasing the amplitude of the wave, while less often by an increase visible period. Since the observation base L2 used in the probes has a relatively small length, which is done in order to increase the spatial resolution in the study of a thin layered geo-acoustic medium, this fact limits the measurement accuracy both of the propagation velocity of the wave V and attenuation decrement Q-1. We attempted to develop a measurement technique with improved accuracy both for the seismic velocity and the decrement of the attenuation of the sounded geo-acoustic medium. This technique is based on the use of information on the total length of the wave trajectory (from the source to the far geophone L=L1 + L2), the essence of which is to analyse the changes in the signal of the far geophone when the probe moves in the borehole. Another way of realizing the maximum length of the probe, which does not require structural changes, was also successfully tested. This way is based on the use of the change in the spectral relationships (and hence the shape) of the broadband probing signal, which take place in the absorbing and scattering media. Indeed, a greater attenuation of the high-frequency components of the spectrum, compared to low-frequency components, leads to a decrease in the central frequency of the spectrum fc. A consequence of this is the elongation of the “visible” (apparent) period of the pulsed probing signal Tv=1/fc. Using this effect, leads to the following formula:
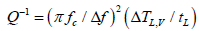 (1)
(1)
Where:
Δf - The width of the frequency band of the probing signal;
ΔTL,V - The increment of the “visible” period that occurs when the wave propagates in the time interval tL.
The relative value of the frequency spectrum of the signal represents the sensitivity of this method.
Method for Studying the Fracturing of the Probed Geoacoustic Medium on the Basis of Analysis of Information about the Measured Speed Parameters
Among the possible physical criteria that can be used to obtain information about the existence of directed fractures in rocks, the anomalous value of Poisson’s ratio KPoiss is quite obvious. In fact, in the plate environment, which is actually a mechanical equivalent of a continuous solid body, dissected by a system of parallel fractures, the value of KPoiss in a direction orthogonal to the surface of the fractures should be minimal, and in the direction of the surface of the fractures, the maximum. In the acoustic logging method, the Poisson ratio can be determined according to the measurement of the ratio of the sound velocities of the transverse Vs and the longitudinal Vp waves [6-8]:
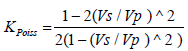
Since the minimum value of KPoiss occurs at the maximum of the ratio Vs/Vp, then it is the determination of the Vs/Vp ratio from the log analysis of seismic wave velocities that carries information about the Poisson’s ratio. Unfortunately, the value of KPoiss depends not only on the presence of fractures, but also on the material composition of the probed medium. Actually, if the average value of the Poisson ratio of rocks is KPoiss ~ 0.33 (which corresponds to the ratio Vs/Vp=0.5), then in viscous “water-like” rocks of clay type, the value of the Poisson’s ratio is much higher, and in brittle “plug-like” rocks such as limestone and sandstone, on the contrary, lower. Therefore, the range of variation of the Poisson’s ratio, due to the change in the real composition of the probed medium, is an obstacle in the study of the fractures by the method of analysing the Poisson’s ratio. The magnitude of this range is quite significant. For example, for oil well, the range of variation in KPoiss along the depth of the well is approximately 20%, while the effect of fractures on the KPoiss value is significantly smaller. Therefore, when analysing the presence of fractures, it is correct to take into account not the absolute value of the KPoiss values, but either its deviation from the average value for a given rock type or its dependence on the direction of probing. If neither of these is possible, then we must use other methods of studying the fractures and, first of all, by analysing the attenuation of the probing waves.
Method for Studying the Fractures of the Probed Geoacoustic Medium Based on the Information Analysis of the Measured Attenuation Parameters
Study of the influence of micro heterogeneous inclusions on the characteristics of a geo-acoustic medium, carried out by means of physical modelling, has showed that among the parameters of velocity and Q factor, the Q factor has a higher sensitivity to the influence of micro-heterogeneous inclusions. Thus, in the case of studying the porosity coefficient [5], it was found that when using the attenuation decrement as the output measured value, the sensitivity with respect to the change in the porosity coefficient is Q (Q-factor) times higher than with respect to the change in one of the velocity parameters. When working in high-quality rocks, including most reservoir rocks, this means a very significant advantage of the “attenuation method” - for one to two orders of magnitude. The qualitative aspect of the influence of directional fractures on attenuation of seismic waves is visible on seismograms (Figure 1). The increase in decrement leads to a drop in the amplitude and apparent period increase (a decrease in the upper boundary of the frequency range) of the measurement signal for the longitudinal wave. As can be seen, the minimum attenuation occurs when the medium is probed along the fractures (? →0). When ? > 0, the magnitude of the attenuation increases, reaching its maximum when ? → π/2, i.e., with the direction of the probing beam orthogonal to the direction of the fractures, and hence orthogonal to the well axis.
Method for Determining the Rocks Attenuation Parameters from the Ratio of the Amplitudes of the Longitudinal and Transverse Waves
Method for processing acoustic log data was developed, which was based on the use of the ratio of the amplitude of the longitudinal and transverse waves of the probing signal Up/Us [6]. Unfortunately, the authors do not give a physical explanation for the work of their proposed method. In our opinion, the dependence of the ratio Up/Us should be sought in the difference in the decrements of the attenuation of the longitudinal and transverse waves. Since the measurement of the amplitudes of the probing signal waves is a simple technological procedure, it is logical to apply this method to evaluate the fractures of the probed rocks. We use the expressions for amplitudes of the probing signal of acoustic logging in the following form:
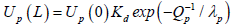 (2)
(2)
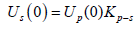
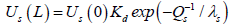 (3)
(3)
Where;
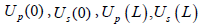 : The amplitudes of the longitudinal and transverse waves at the distances L=0 and L respectively.
: The amplitudes of the longitudinal and transverse waves at the distances L=0 and L respectively.
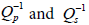 : The decrements in the attenuation of longitudinal and transverse waves.
: The decrements in the attenuation of longitudinal and transverse waves.
λp and λs: The lengths of the longitudinal and transverse waves.
Kp-s: The conversion coefficient of the longitudinal wave to the transverse wave.
Kd: The divergence coefficient.
Based on Eq.2 and Eq.3 we obtain:
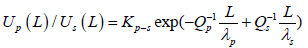 (4)
(4)
Representing an approximately exponential function in the form of a power series, we get:
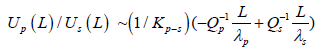 (5)
(5)
In the presence of fractures having a direction orthogonal to the direction of the probing wave, the attenuation decrement of the longitudinal wave exceeds the decrement of the transverse wave: 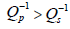 . Furthermore, the length of the transverse wave is usually twice as long as the longitudinal wave. Therefore, in the case under consideration, with an acceptable approximation, we can put
. Furthermore, the length of the transverse wave is usually twice as long as the longitudinal wave. Therefore, in the case under consideration, with an acceptable approximation, we can put
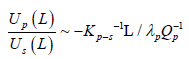 (6)
(6)
Thus, the ratio of 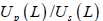 is proportional to the decrement of attenuation of longitudinal waves and hence can be used as a measure of fracturing. Note that the amplitude of the probing signal is a parameter easy to measure, minimally susceptible to errors and failures. The wave fields shown in Figure 1 refer to structures cut by gas-filled fractures. However, by simple logical reasoning, they can be extended to structures in which the filler of the fractures is a liquid (oil or water). Actually, taking into account, that the replacement of gas with liquid has very little effect on the wave fields of transverse waves, since the wave impedance in the interior of a fractured medium Z=ρ V remains close to zero. This is because the velocity of the transverse waves Vs in the liquid is also zero, as in the gas. In contrast to this, for longitudinal waves, the acoustic wave impedance in the interior of a fractured medium Z, when the gas is replaced by a liquid significantly increases. This will significantly reduce the anomalous effects for both velocity and attenuation.
is proportional to the decrement of attenuation of longitudinal waves and hence can be used as a measure of fracturing. Note that the amplitude of the probing signal is a parameter easy to measure, minimally susceptible to errors and failures. The wave fields shown in Figure 1 refer to structures cut by gas-filled fractures. However, by simple logical reasoning, they can be extended to structures in which the filler of the fractures is a liquid (oil or water). Actually, taking into account, that the replacement of gas with liquid has very little effect on the wave fields of transverse waves, since the wave impedance in the interior of a fractured medium Z=ρ V remains close to zero. This is because the velocity of the transverse waves Vs in the liquid is also zero, as in the gas. In contrast to this, for longitudinal waves, the acoustic wave impedance in the interior of a fractured medium Z, when the gas is replaced by a liquid significantly increases. This will significantly reduce the anomalous effects for both velocity and attenuation.
Attenuation Mechanism of Seismic Waves in Porous Rocks on the Principle of Dispersion (Reemission of Seismic Waves by Inertial Forces Arising on Microheterogeneous Inclusions of Reduced Density)
Of the two possible anomalous effects of rocks, seismic velocity and attenuation, exploration geophysics more often uses seismic velocity. The parameter of attenuation is still given much less attention. Using a means of ultrasonic seismic modelling, a series of experimental studies was previously carried out, showing that the attenuation decrement has a much higher sensitivity to the porosity parameter than the parameter of the seismic velocity. However, the results of these experiments could not be linked to the results of the theoretical analysis at that time. The fact is that in classical works on acoustics, the central place is occupied by works on the study of the regularities of the propagation of waves in gases and liquids. In General works such as encyclopedic monographs [7], a review of the achieved results concerning the study of regularities of the attenuation of the sound waves is limited to objects that are liquid enclosing medium and micro-heterogeneous inclusions of very small dimensions. The final conclusions in this work cannot be used in analysing the propagation of waves in rocks. So, for example, the widely known conclusion from popular acoustics about the transparency of small-sized obstacles for probing sound waves can only mislead geophysicists. The theoretical analysis, in the recent geophysical work [8-11], was carried out using significant simplifications and approximations, qualitatively changing the real physics of propagation of sound waves in rocks. For example, in order to realize an approximate solution of the equation of motion of a flowing fluid, micro-heterogeneous inclusions consider in the form of ellipsoids of rotation, which is an unacceptable simplification for most objects of interest to practical oil and gas geophysics [12]. Experiments of physical modelling have shown that the mechanism of viscous friction plays a secondary role in the attenuation of seismic waves in highly porous rocks. This is confirmed by the following fact: Substitution within the fractures and pores of low viscosity water with high viscosity oil has little effect on attenuation, and replacing any liquid with a gas having a very low viscosity leads even to an increase, and not to a decrease in attenuation. An analysis of the experimental facts leads to the conclusion that the main reason for the significant attenuation of seismic waves in porous and fractured rocks is the effect of their dispersion. This is due to the appearance of a force field on the “soft” (with respect to the surrounding medium) micro-heterogeneous inclusions, randomly located inside the oil and gas reservoir. To prove this, let us consider the wave field that arises when a porous geoacoustic medium is probed with a plane harmonic sound wave having an oscillatory velocity 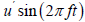 . This wave corresponds to the acceleration
. This wave corresponds to the acceleration 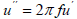 and the pressure
and the pressure  [7]. Where V0 and ρ are the seismic velocity and density of the medium. The dependence of pressure on the vibrational velocity is called the acoustic Ohm’s law. Some i-th element of the medium under consideration, having volume Vi and correspondingly the mass of
[7]. Where V0 and ρ are the seismic velocity and density of the medium. The dependence of pressure on the vibrational velocity is called the acoustic Ohm’s law. Some i-th element of the medium under consideration, having volume Vi and correspondingly the mass of 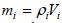 , as a result of the action of acceleration
, as a result of the action of acceleration 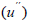 acts on the host medium with the force
acts on the host medium with the force 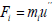 According to the condition of chaotic distribution in a medium of micro-heterogeneous inclusions, and hence, of secondary force sources, the latter are independent. Each power source emits oscillatory displacement
According to the condition of chaotic distribution in a medium of micro-heterogeneous inclusions, and hence, of secondary force sources, the latter are independent. Each power source emits oscillatory displacement 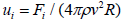 [13], which physically means the energy extraction from the source of the probing wave, and hence the occurrence of attenuation, decrement value which can be estimated as follows. The decrease in the amplitude of the wave
[13], which physically means the energy extraction from the source of the probing wave, and hence the occurrence of attenuation, decrement value which can be estimated as follows. The decrease in the amplitude of the wave 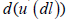 on a small space interval dl, dl, which is determined as a consequence of the pressure drop d( p(dl )) on the basis of the acoustic Ohm’s law and a value of the wave resistance V0, is equal to
on a small space interval dl, dl, which is determined as a consequence of the pressure drop d( p(dl )) on the basis of the acoustic Ohm’s law and a value of the wave resistance V0, is equal to
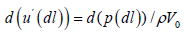 (7)
(7)
The value of the pressure drop d( p(dl )) is the result of the action, on the space interval dl, of the sum of elementary sources of forces F:
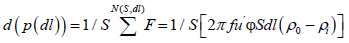 (8)
(8)
Where;
N(S, dl): The number of elementary power sources Fi in the volume of the propagation space of the Sdl.?: The coefficient of porosity.
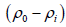 : The difference between the density of the enclosing rock ρ0 and the density of the interstitial fluid ρi.
: The difference between the density of the enclosing rock ρ0 and the density of the interstitial fluid ρi.
Further, passing from a small spatial interval dl to an interval of finite length L, we obtain: 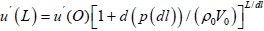
Given that for small arguments of the function x is exp x~ (1 +x) and hence (1+x)N ~ Nx, and also taking into account the ratio of f/ u´=1/λ (where λ is the wave length), we get:
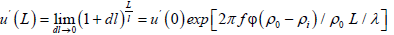 (9)
(9)
In acoustics, the traditional expression for the attenuation of a sound wave is the relation;
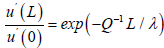
Where Q-1: The attenuation decrement.
Comparison of this relation with Eq. 9 shows their compliance with the value of the decrement equal to
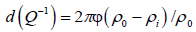 (10)
(10)
Thus, the attenuation decrement of the porous rocks is equal to the product of the coefficient of porosity by the difference relative density of interstitial fluid. Let us pay attention to the fact that neither the dimensions, nor, the more so, the shape of the micro-heterogeneous inclusions, do not affect the magnitude of the decrement. The influencing factor is only the cumulative volume of microheterogeneous inclusions, which is the porosity of the probed geoacoustic medium. In real rocks, the relative density of the interstitial fluid varies in relatively narrow limits-from 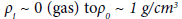 (water). Therefore, the maximum relative change
(water). Therefore, the maximum relative change 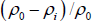 in the attenuation value Q-1 is not more than 30%. This makes it difficult to diagnose the material composition of the interstitial fluid according to the parameter Q-1. Here, electromagnetic methods have advantages over acoustic ones. As for the possibility of diagnosing the porosity coefficient, then, as follows from Eq.10, the attenuation effect is a very convenient factor for its determination. We did not take into account the attenuation value that takes place in a “continuous” (devoid of pores) geo-acoustic medium, assuming that Q−1(?→0)→0 . In the oil and gas geophysics this assumption is close to the truth, since the attenuation decrement of consolidated rocks usually does not exceed several hundredths Q−1(? ~ 0) < 0.05 . It should also be noted that it is possible to introduce an amendment to the attenuation of waves in a continuous medium, using the statistical relationship between the decrement and the seismic velocity of rocks. The latter can be approximated by an empirical relation [14];
in the attenuation value Q-1 is not more than 30%. This makes it difficult to diagnose the material composition of the interstitial fluid according to the parameter Q-1. Here, electromagnetic methods have advantages over acoustic ones. As for the possibility of diagnosing the porosity coefficient, then, as follows from Eq.10, the attenuation effect is a very convenient factor for its determination. We did not take into account the attenuation value that takes place in a “continuous” (devoid of pores) geo-acoustic medium, assuming that Q−1(?→0)→0 . In the oil and gas geophysics this assumption is close to the truth, since the attenuation decrement of consolidated rocks usually does not exceed several hundredths Q−1(? ~ 0) < 0.05 . It should also be noted that it is possible to introduce an amendment to the attenuation of waves in a continuous medium, using the statistical relationship between the decrement and the seismic velocity of rocks. The latter can be approximated by an empirical relation [14];
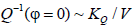
Where V is the velocity of sound and KQ is an empirical coefficient.
Since the value of the seismic velocity V is usually well known, it is possible to consider the initial value of the decrement Q−1(? = 0) . That allows specifying the part of decrement of which porosity is introduced into the medium of its total value (Q−1Σ) .
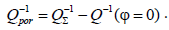
With the purpose of studying the regularities determining the effect of the rock porosity on the attenuation of seismic waves, a series of laboratory experiments using means of physical (ultrasonic) modelling was carried out earlier [5]. To this end, a group of physical models containing micro-heterogeneous inclusions (pores), filled with either gas or liquid (oil or water), has been developed. The experiments were carried out with two-dimensional (sheet) and three dimensional (volumetric) models. Two-dimensional models were built on the basis of thin sheet of aluminium. Such models were equivalent to two-dimensional (cylindrical) of the enclosing environment. Microheterogeneous gas-filled inclusions were imitated by perforations in the body of the sheet. The main type of three-dimensional (volumetric) models was built on the principle of a mixture of foam plastic granules and epoxy resin. Such models correspond to rocks containing gas-filled pores. When the size of the foam plastic granules is of the order of 1 to 4 mm and the wavelength of the probing signal is 5 to 50 mm, the condition for the smallness of the dimensions of the micro-heterogeneous inclusions with respect to the wavelength of the probing signal is always attained under natural conditions of seismic probing. The coefficient of porosity of such a medium is equal to the volume of foam granules in relation to the volume of epoxy resin. The models were prepared in the form of rectangular blocks having dimensions 250 ? 250 ? 28 mm3. The foam plastic inclusions represented granules of the order of 1 x 1 x 1.5 mm3. Four blocks were prepared in which the porosity coefficients were φ=0.8, 16 and 23%.The experiments were carried out on longitudinal waves. Each block was placed in an aquatic medium, in which it was transmitted through an ultrasonic wave. The central frequency of the probe pulse was chosen within the range of f ∼130-300 kHz. The wavelength in the epoxy resin was 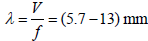 . The obtained measurement results are summarized in Table 1. The experiment shows the qualitative agreement of the attenuation decrement values obtained experimentally and analytically.
. The obtained measurement results are summarized in Table 1. The experiment shows the qualitative agreement of the attenuation decrement values obtained experimentally and analytically.
| Pororsity, φ | 0 | 0.08 | 0.16 | 0.23 |
| Qtheor(-1)=2πφ | 0 | 0.5 | 1.0 | 1.45 |
| Uwater/Uφ | 1.03 | 2.18 | 4.75 | 3.9 |
| fv, Hz | 140 | 187 | 140 | 140 |
| λv, mm | 14.3 | 14.35 | 19 | 19.5 |
| Qexp(-1)=λv/L ln(Uwater/Uφ) | 0.015 | 0.4 | 1.08 | 0.94 |
Table 1: The obtained measurement results.
Conclusions
In geological structures, vertical pressure prevails over horizontal pressure. Therefore, the opening of vertical fractures exceeds the opening of horizontal fractures and the permeability of reservoirs for horizontal wells is higher than for vertical ones.
The highest sensitivity with respect to the factor of presence of fractures is the criterion of wave attenuation. For longitudinal waves, the attenuation decrement has a strong dependence on the direction of the ray (beam) relative to the plane of the fractures. The change in the decrement takes place from the minimum that occurs when the direction of wave propagation close to the direction of the surface of fractures, up to a maximum that occurs in the orthogonal direction. For the transverse waves, the attenuation decrement is practically independent of the direction of propagation of the wave.
A method for measuring the decrement of the attenuation of longitudinal waves, and hence the study of fractures in the method of acoustic logging, is a method based on measuring and interpreting the ratio of the amplitudes of the longitudinal and transverse waves of the probing signal.
In the present work, an attempt is made to explain the cause of high attenuation of seismic waves in a porous medium on the basis of the mechanism associated with the appearance of a force field on “soft” micro-heterogeneous inclusions. In this case, the increment of the attenuation decrement is expressed by the product of the porosity coefficient by the relative density of the interstitial fluid.
For highly porous oil and gas reservoir rocks, the attenuation decrement due to this mechanism is ten times higher than the decrement value due to other mechanisms.
The attenuation decrement for a given mechanism does not depend on the shape of the incoherent inclusions, but also on the frequency and amplitude of the probing signal.
References
- Kashevarov AA, Eltsov IN, Epov MI (1996) Hydrodynamic model of formation of the penetration zone in well drilling.Vol-44,pp: 148-157.
- Yeltsov IN, Kashevarov AA, Reshetova GV, Cheverda VA (2004) The manifestation of the heterogeneous features of the zone of penetration of geophysical fields along a well bore Geophysics, pp: 17-21.
- Smekhov EM, Dorofeeva TV (1987) Secondary porosity of reservoir rocks oil and gas,p: 180.
- Dobrynin VM, Wendelshtein B, Kozhevnikov Y, Rosh DA (1999) The role of petro physics in the identification and study of oil and gas deposits. NTV "Logging" Tver, pp: 15-30.
- Gik LD (1997) Physical modelling of seismic propagation waves in porous and fractured media Geology and geophysics,pp: 804-815.
- Koksharov VZ, Nefedkin Yu, A Bazelev, Suzdalnitsky FM (1996) Prospects for the use of frequent acoustic probing for separating gas-saturated intervals and studying complex reservoirs fields,p: 86.
- Isakovich MA (1973) General Acoustics,p: 496
- Lynn ??, Ca?pagna D, Si?on ??, Beckha? WE (1999) Relationship of P-wave seismic attributes azimuthal anisotropy commercial gas ??? in 3-D P-wave multi azimuth data Rulison field Piceance Basin. Colorado Geophysics, 64: 1293-1311.
- Hudson JA (1981) Wave speeds and attenuation of elastic waves in material containing cracks. Geophysics J Int, 64: 133-150.
- Bakulin AV,Molotkov PA (1998) Effective seismic models fractured and porous media.SPb Un-ta,p: 141.
- Bakulin ?,Grechka V,Tsvankin I (2000) Estimation of fracture parameters from reflection of seismic data Part 1: HTI model due to ? single fracture set.J. Geophysics, 65: 1788-1802.
- Chichinin TI,Sabinin VI,Ronkiyo-KharijoKh,Obolentseva IR (2006) QVOA method to search for fractured reservoirs. Geology and geophysics,pp: 259-277.
- Luzyrev NN,Trigubov AV, Brody LYu(1985) Seismic exploration by the method of transverse and exchange waves M: Nedra,p: 278.
- Gurvich VP,Nomokonova (1981)Seismic prospecting: Handbook of Geophysics. MNedra, p: 464.
Relevant Topics
Recommended Journals
- Oil & Gas Research Journal
- Renewable Energy and Applications Journal
- Oceanography Journal
- Industrial Pollution Control Journal
- Coastal Zone Management Journal
- Climatology & Weather Forecasting Journal
- Geoinformatics & Geostatistics Journal
- Engineering and Technology Journal
- Petroleum & Environmental Biotechnology Journal
- Polymer Sciences Journal
Article Tools
Article Usage
- Total views: 2925
- [From(publication date):
August-2017 - Aug 01, 2025] - Breakdown by view type
- HTML page views : 2029
- PDF downloads : 896

