Research Article Open Access
Actions and Strategies for the Urban Pollution Produced by Heating Plants
Nicoletti G*, Bruno R, Arcuri N and Nicoletti G
Department of Mechanical, Energetic and Management Engineering, University of Calabria, 87030 Arcavacata Di Rende (CS), Italy
- *Corresponding Author:
- Nicoletti G
Department of Mechanical, Energetic and Management Engineering
University of Calabria, 87030 Arcavacata Di Rende (CS), Italy
Tel: +3909844911
E-mail: giovanni.nicoletti@unical.it
Received date: September 04, 2015; Accepted date: October 16, 2015; Published date: October 20, 2015
Citation: Nicoletti G, Bruno R, Arcuri N, Nicoletti G (2015) Actions and Strategies for the Urban Pollution Produced by Heating Plants. Oil Gas Res 1:102. doi: 10.4172/2472-0518.1000102
Copyright: © 2015 Nicoletti G, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Oil & Gas Research
Abstract
In urban areas, the emission of pollutants produced in combustion processes causes the air contamination. Regarding traditional combustion products released from heating plants of residential sector, a study on their environmental impact and the proposal of appropriate strategies for urban pollution reduction, has been carried out. In the first part, some initiatives to reduce urban air pollution linked to heating systems operation, in order to increase the livableness of cities, are proposed. In the second part, a quantitative comparison among different fossil fuels which supply heating plants, both under the environmental and safety points of view, has been carried out. The investigation has included solar-hydrogen as new and cleaner energy carrier for the future. At this purpose, suitable quality indexes which measure the flammability and the expansiveness characteristics of the fuels have been introduced. Another quality index was used in order to evaluate the environmental impact, by considering the pollutant substances produced during the combustion reaction. Finally, a classification among the considered fuels was determined by means a global impact index, which summarizes all the mentioned aspects. An economic analysis involving the real costs of considered fuels was carried out by moving the focus of the investigation to the end of the process of energy production, and by extending the evaluation of the real costs by including the effects produced from the final use.
Keywords
Urban pollution; Fuels; Chemical pollution; Heating plants
Introduction
The problem concerning urban pollution has assumed great importance by considering the damages that it provides to people and to the surroundings [1]. The urban pollution has reached dangerous levels and in winter it is mainly generated by the polluted substances produced in combustion processes which occur in heating systems of the residential sector [2]. These emission sources are classified as permanents, such as furnaces, incinerators and industrial boilers, in opposition to mobile sources such as cars and conveyances [3]. In this paper, an investigation on the urban atmospheric pollution generated by heating systems is carried out. Nowadays, the building heating needs are satisfied mainly by fossil fuels such as methane, diesel oil and, especially in the emerging countries, coal [4]. These fuels, during the combustion process, contribute to the urban pollution by releasing in atmosphere mainly carbon oxides, nitrogen oxides, sulphur oxides, volatile organic compounds (VOC) and solid particulate (SP). During the combustion process, other substances as heavy metal and dioxin are released [5], but in the present work they are not considered despite their noticeable impact from the sanitary and ecological point of view [6]. The Table 1 reports the quantities of CO2 and other pollutants emitted in the major industrialized countries considering the residential, industrial and transportation sectors [7].
| Countries | Pollutants from combustion reactions (in 103 tons/year) | ||||
|---|---|---|---|---|---|
| Sulphur dioxide | Nitrogen oxides | Particulate | Carbon oxide | Carbon dioxide | |
| SO2 | NxOy | [SP] | CO | CO2 | |
| U.S.A. | 23 200 | 20 300 | 8 300 | 77 400 | 4 166 000 |
| Japan | 1 314 | 1 435 | - | - | 831 000 |
| Germany | 3 200 | 3 100 | 725 | 8 650 | 666 000 |
| United Kingdom | 4 670 | 1 812 | 442 | 8 891 | 517 000 |
| France | 3 460 | 1 847 | 278 | 5 200 | 404 000 |
| Italy | 3 205 | 1 506 | 433 | 5 487 | 322 000 |
| Spain | 3 756 | 792 | 1 521 | 3 780 | 198 000 |
| Holland | 450 | 525 | 150 | 1 450 | 130 000 |
| Belgium | 856 | 317 | 267 | 839 | 107 000 |
Table 1: Comparison between the pollutant emissions provided by fossil fuel combustions in the more industrialized countries.
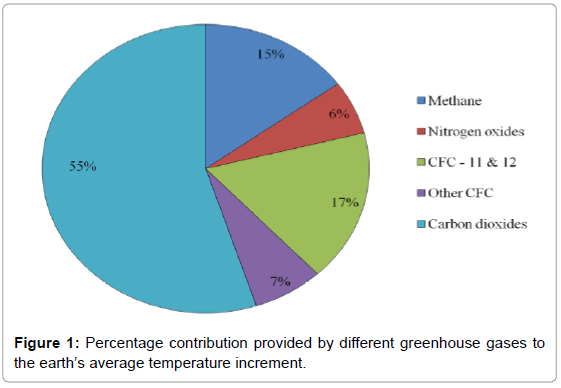
With reference to the CO2 emissions, the more important data is the increment registered in the period 1890-2014 from about zero to 22·1012 kg/year, correspondent to 360 ppm or 800 mg/Nm3 [8,9]. On the other hand, the CO2 concentration together other gases, contributes for the 55% to form the greenhouse effect, as represented in Figure 1 [8]. Other substances as nitrogen oxides and unburned methane, supplied by heating plants, contribute to external air temperature growth producing in the cities the so-called effect of “heat island”.
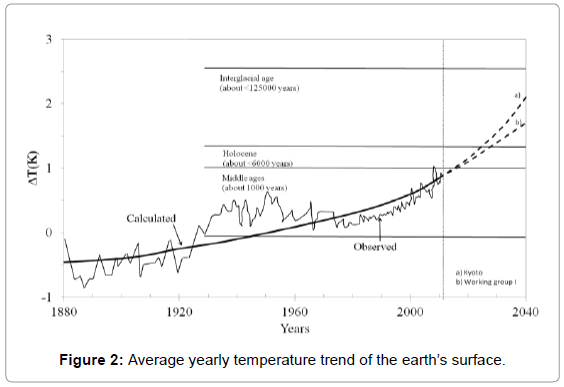
The trend in global temperature due to the increase of CO2 in the atmosphere, adjusted considering the part absorbed by the oceans and the mainland, is shown in Figure 2 [8-10].
The exploitation of innovative fuels with low environmental impact, as the solar hydrogen produced by electrolysis process, could reduce the pollutant levels in urban areas, especially CO2 [11,12], but in the short period the requalification of the existing heating plants seem to be more promising to limit the pollutant concentrations [13].
In the first part of the paper, some initiatives that local administrations could undertake to reduce the urban pollution, are proposed. These initiatives are in opposition with the adopted current policies, such as the realization of pedestrian areas and the closure to the cars of the cities. New environmental policies must consider a prudent employment of fuels, also considering the possibility to exploit electric heating, control and requalification of old heating plants, employment of cleaner fuels and, finally, realization of green islands able to absorb the CO2 emitted. In the latter case, if the required spaces are not available, an interesting solution is represented by green roofs made over existing buildings [14]. Therefore, incentivizing policies to requalify the old building-plant systems are desirable. In the long period, the use of hydrogen as alternative and clean energy carrier appears suitable when the traditional fuels will be depleted or when the pollution concentrations reach alarming levels.
Moreover, in order to evaluate quantitatively the advantages concerning the hydrogen exploitation, in the second part of the paper a comparison between solar hydrogen and different fossil fuels, is carried out both on the point of view of the environmental and of the safety aspects. The environmental properties of the investigated fuels were determined analytically by means an environmental impact index evaluated in function of the emitted pollutant substances. The aspects concerning the safety, such as the flammability and the expansiveness, have been quantified by introducing other indexes which take into account the thermodynamic characteristics of fuels. The proposed indexes have been summarized in a unique value to determine a score and in order to realize a classification among the investigated fuels. The latter values are dimensionless and they range between 0 and 1: the latter score is reached when pollutant substances are not emitted and when the better safety conditions are achieved.
Hydrogen currently could be used for heating applications by mixing it with traditional fuels in appropriate boilers or in cogenerative fuel cells, but economic unfeasibility reasons impede its exploitation. The cost of hydrogen appears more competitive if the “hidden” ones related to the fossil fuels employment, linked to the health problems caused by air pollution, the damage generated by fuel mining and the correspondent environmental degradation, are included in the fuel final cost. Therefore, an analysis carried out with the concepts of the so-called “real economy” has been conducted in order to move the cost evaluation at the final phase of the fuel exploitation. The solar-hydrogen produced by electrolysis presents a cost for unity of produced energy of about 0.191 €/kWh by including photovoltaic fields and electrolyzer [15], consequently the obtained value is itself more 2-4 times higher than the cost obtained through exploitation of conventional fossil fuels, without considering the additional costs of hydrogen retransformation into electrical energy. In fact, with reference to the European sector of power generation, in 2013 an average levelized cost of electricity between 0.059 €/kWh (coal) to 0.086 €/kWh (combined power plant fired by methane) is reported [16]. By including in the global process the costs related to the social and environmental aspects, the aforementioned gap results more limited [17]. Therefore, the final costs of the investigated fuels have been evaluated in function both of the fuel market prices and of the produced environmental damages.
Possible interventions for the control of the urban pollution
The first and more obvious measure in heating plants is the gradual replacement of traditional fuels [18] with other fuels or by mixing them with fuels at lower environmental impact. Table 2 lists for the Italian situation the type of pollution emissions in function of the fuel type [19].
| Fuel | Consume (%) | SOx (%) | NxOy (%) | Particulate (%) | CO (%) |
|---|---|---|---|---|---|
| Diesel Oil | 38.6 | 89.5 | 53.8 | 76.1 | 94.5 |
| Coal (lignite) | 10.1 | 9.1 | 7.4 | 2.4 | 0.3 |
| Natural gas (methane) | 38.3 | 0.0 | 36.9 | 10.3 | 0.3 |
| Other fuel | 0. 8 | 2.4 | 1.9 | 11.2 | 4.9 |
| Electricity* | 12.2 | -- | -- | -- | -- |
*By supposing the electricity as a direct primary source.
Table 2: Some pollution emissions in Italy with reference to the year 2010 in function of the type of primary source related to residential and industrial sectors.
In the prior table the CO2 emissions are not reported since usually they are associated to a global environmental damage and it is very difficult to assess the part of carbon dioxide connected with the heating plants [20,21]. Currently, fuel consumption in Italy involves mainly methane and diesel oil: the latter is widely used to supply centralized heating plants in large buildings. Therefore, a preliminary measure is the replacement of diesel oil by means methane, so that a considerable reduction of SO2 and SP could be achieved. The latter action is easy reachable considering of the diffusion of the methane pipelines in the cities and of the necessity to replace the old and obsolete diesel oil boilers, since the majority has been installed in the sixties and seventies of the last century. Therefore, an adequate policy to stimulate the diffusion of methane boilers in existing plants, especially the condensation ones, is desirable. Since the combustion temperatures achieved in modern methane boilers are limited, a considerable reduction of the NxOy emission could be also achieved.
An unusual but promising measure for the long period is the exploitation of hydrogen, pure or mixed with traditional fuels, as primary source in heating plants [22]. Hydrogen combustion provides mainly water vapor and, if the air is the oxidizing substance, nitrogen oxides and a few of photochemical oxidants [23]. The various research activities conducted with hydrogen in the last years allow to formulate [24-28]:
a. Hydrogen combustion provides a hot, clean and stable flame, therefore appropriate burners and flue chimneys are not required;
b. Since hydrogen transportation network requires pressures of 70-100 bar, of the same order for the methane supply, adequate modifications on the existing pipelines could allow the hydrogen transportation [29,30];
c. Many technical problems have been solved, considering the practical applications in the space engineering, in the propulsion of submarines, in the gas turbines and in the supersonic aircrafts;
d. The hydrogen storage has reached a sufficient technological level, both in liquid phase and in high pressure systems;
e. The improvement and the diffusion of the solar technologies will allow the reduction of the cost related to electrolysis processes; in Italy, for instance, the cost of PV technologies was reduced by 300% in the last five years [28].
A third way to reduce the urban pollution is the employment of electric heating systems, especially of radiant type, replacing old and obsolete heating plants [28]. From a thermodynamic point of view, these systems in these situations appear profitable, considering the increment of electric energy produced from renewable sources and the improvement of the power plants efficiency supplied by fossil fuels. In precautionary way, to evaluate the global efficiency and the correspondent costs related to the production (with fossil fuels) and the distribution of electric energy, supposing of a unitary efficiency of the emission terminal for electric heating applications, the following value is obtained:
ηtot = ηcomb·ηterm·ηtran·ηdist = 0.95·0.50·0.95·0.95 = 0.4286
where ηcomb is the boiler efficiency in the power plant, ηterm is the thermodynamic efficiency (combined cycle), ηtran is the alternator efficiency and ηdist is the efficiency of the electric transportation network. The obtained value is slightly lower than the current efficiency of the Italian electric system of 0.46 [29]. If the fossil fuel employed in the power plant is used directly in an obsolete boiler of a heating plant, hypothesizing an average seasonal generation efficiency value ηgen of 0.65, and values of 0.90 respectively for the efficiencies related to the distribution of the hot water (ηdist), the storage system (ηstor), the control (ηcont) and the emission (ηemist) subsystems, the following global efficiency is obtained:
ηtot. = ηgen·ηstor·ηdist·ηcont·ηemis = 0.4264
The two obtained global efficiencies are widely comparable, therefore the advantages concerning the direct use of fossil fuels in an autonomous or centralized plant with obsolete technologies are really limited compared with the production of electric energy in a modern power plant. Moreover, from the point of view of the environmental impact, the exploitation of electric energy for heating applications leads to a pollutants production focused in a unique location, usually placed far from the cities, rather than a distributed emission of pollutants inside the urban areas.
Comparison among the investigated fuels: environmental and safety aspects
A quantitative comparison be tween the considered fuels which take into account the environmental and safety characteristics has to consider:
a) The chemical pollution provided by combustion reactions;
b) The flammability related to the dangerousness of the considered fuel;
c) The expansiveness linked to the explosive potential of the same fuels;
For every point, a quality index is introduced and an appropriate combination of these indexes allows the evaluation of a global score required to determine a graded list where appear hydrogen and the considered fossil fuels. The proposed quality indexes have been determined considering of the thermo-physical properties of the fuels [30-32] (Table 3) and the produced pollutants during the combustion reactions with air as oxidant substance (Table 4) [33,34]. The thermophysical properties of the carbon reported in Tab. 3 concern the values of its oxide.
| Fuel | Specific Heat cp (kJ/kg∙K) |
Specific Volume v (m3/kg) |
Lower heating value LHV (kJ/kg) |
Combustion Temperature Tc (K) |
Flammable Temperature T0 (K) |
|---|---|---|---|---|---|
| Methane | 2.218 | v''' = 1.40 v'' = 0.00625 |
50000 | 1745 | 632 |
| Diesel Oil | 2.243 | v''' = 1.20 v'' = 0.015 |
43600 | 1573 | 1073 |
| Coal | 1.100 | v''' = 0.8 v'' = 0.006 |
33500 | 2000 | 609 |
| Hydrogen | 14.270 | v''' = 11.2 v'' = 0.0325 |
120000 | 2332 | 571 |
Table 3: Thermo-physical properties of the investigated fuels (v’’= liquid phase, v’’’=gaseous phase).
| 1 | 2 | 3 | 4 | ||
|---|---|---|---|---|---|
| Fuels | CO2 [g/kg] |
SO2 [g/kg] |
NOx [g/kg] |
Particulate [g/kg] | |
| a | H2 | 0 | 0 | 0 | 0 |
| b | C | 3195.9 | 15.6 | 46.8628 | 4.6199 |
| c | CH4 | 2745 | 0.0205 | 2.1005 | 0.001 |
| d | C8H18 | 3196.8 | 1.1988 | 0.6335 | 0.2419 |
Table 4: Weighted percentage of pollutants in the considered fuels.
Regarding the environmental aspects, the following relation is used to calculate for every fuels the pollution index:
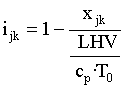 (1)
(1)
where j is the considered fuel (ranging from a to d, see first column of Table 4), k identifies the type of pollutant (varying from 1 to 4, see first row of Table 4), xjk represents the mass concentration of the pollutant substances produced during the combustion (the values listed in Table 4), LHV is the lower heating value of the jth fuel (in kJ/kg, Table 3), cp is its specific heat a constant pressure (in kJ/kg·K, Table 3) and, finally, T0 is the flammable temperature. Concerning the safety aspects, the following dimensionless index is initially proposed to quantify the flammable characteristics of the considered fuels:
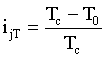 (2)
(2)
where Tc is the combustion temperature of the considered fuel. Another dimensionless index has been used to measure the expansiveness characteristics:
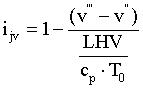 (3)
(3)
where ν’’’’ and ν’’’ are respectively the specific volume of the considered fuel in gaseous and liquid phases.
Economical Evaluations
The final cost of the investigated fuels is determined by summing the market prices and the external costs, opportunely modified in function of the technology employed and of the correspondent pollutant emissions.
The gap between hydrogen and fossil fuels becomes less severe including social and environmental costs associated with the production of energy [35]. By means a comparison with a reference fuel, the real cost of a fuel per unit of energy produced, which includes the efficiency of its final use, can be determined by using the following equation:
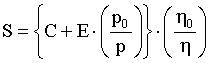 (4)
(4)
where:
- S is the real cost of the unit of produced energy (€/kWh);
- C is the fuel price market per unit of energy delivered to the customer;
- E is the external cost consequent to the fuel use per unit of energy, expressed in current money;
- p is a weight factor introduced to compare different combustion reaction for an environmental point of view;
- η is the utilization efficiency of the device which employs the fuel;
- po, ηo are the correspondent values for the reference fuels.
The E values have been obtained from literature of Lvovsky [36] by a suitable analytical tool that allows to generalize the cost of the environmental damage starting from the calculations carried out in accurate way for six big city of emerging countries. The weight factors for the external costs linked to the environmental damage have been set equal to the global pollution index calculated for the considered fuels by means Eq. (1). In Eq. (4), the fuel price (C·η0/η) is separated from the environmental damage cost (E·p0·η0/p·η). For heating application in the residential sector, fuel cells have been supposed for the hydrogen exploitation in cogenerative operation, with a global efficiency values η of 0.8, while for the other fuels an efficiency value of 0.9 was used, by hypothesizing heating plants equipped with hybrid boilers (for example Stirling engines) for the production of heat and electricity [37]. The results have been obtained by including in the fossil fuels market price the European average tax charges.
Results and Discussions
For every fuel the global pollution index has been calculated as:
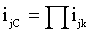 (5)
(5)
The obtained results are listed in Table 5, by supposing standard combustions. In reality, the emission factors depend on the involved technology in the fuel application sector, but the reported values represent default coefficients indicated [38] related to the European situation for the residential heating applications. If the exploitation of the solar-hydrogen occurs in fuel cells, the water vapor must be considered as pollutant substance (because it can be assumed as a greenhouse gas) but in this paper a complete recovery of the produced water is supposed. Moreover, if the fuel cells technology is employed, the environmental impact index of solar-hydrogen has been considered unitary since it burns with pure oxygen. In values listed in Table 6 report the specific result in function of the considered pollutant by applying Eq.(1) and the global environmental impact index by means the Eq.(5). Successively, the obtained values in the last column have been used in Eq.(4) as the weight factor “p” for the economic evaluations.
| Fuels | ij1 | ij2 | ij3 | ij4 | ijE | |
|---|---|---|---|---|---|---|
| a | H2 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1 |
| b | C | 0.8034 | 0.9990 | 0.9971 | 0.9997 | 0.8001 |
| c | CH4 | 0.8386 | 0.9999 | 0.9998 | 1.0000 | 0.8385 |
| d | C8H18 | 0.6573 | 0.9998 | 0.9999 | 0.9999 | 0.6572 |
Table 5: Specific and global environmental indexes obtained for the investigated fuels.
| Fuel | Global index iTOT |
|---|---|
| Methane | 0.928 |
| Diesel oil | 0.834 |
| Coal | 0.925 |
| Hydrogen | 0.827 |
Table 6: Global quality indexes to quantify the environmental and the safety aspect of the considered fuels for heating application in the residential and industrial sectors.
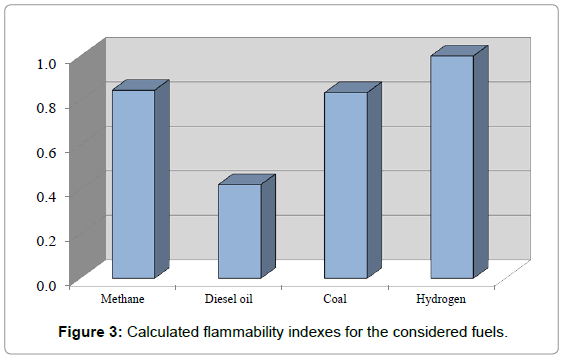
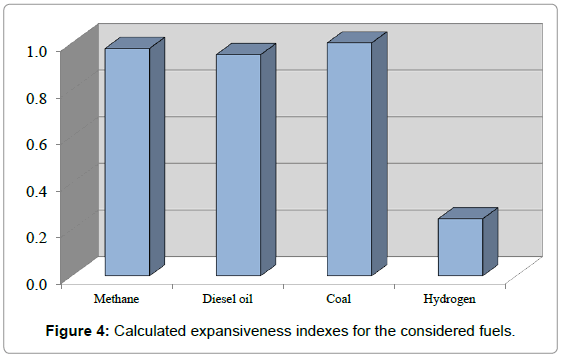
In the Figures 3 and 4 are shown the results obtained for the flammable (i*jT) and expansiveness indexes (i*jV), both normalized in function of the maximum value detected for the considered fuels.
A global impact index which takes into account both the environmental and the safety aspects of the fuel for heating applications can be evaluated by the following equation:
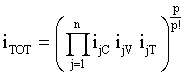 (6)
(6)
The ratio p/p! considers the different employment of the examined fuels in heating systems, where p is the number of factors related to the investigated aspects of pollution and safety (in the specific case p=3). The obtained results are listed in Table 6.
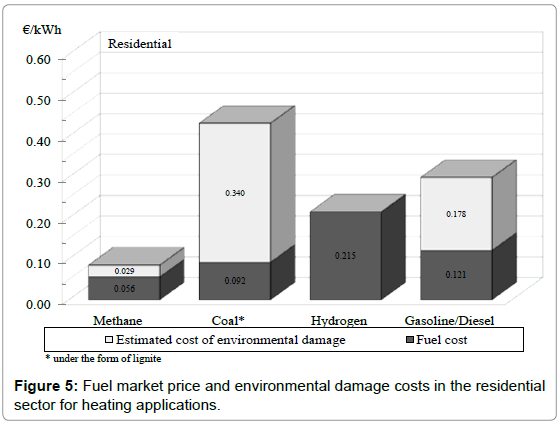
Hydrogen presents the worst position in the ranking, despite the good performances quantified for the environmental aspects, with a final score strongly compromised by bad expansiveness characteristics. For the fossil fuels, instead, the bad performances in terms of environmental impact are compensated by better safety characteristics. Regarding the Eq. (4) which evaluates of the global costs related to the employment of different fuels in heating applications, the results are shown in Figure 5 by differentiating the fuel cost from the environmental damage costs. Moreover, the real costs of the fossil fuels have been compared with the solar-hydrogen, therefore the latter has been set as reference fuel. With these assumptions, solar hydrogen as energy option to supply heating system becomes convenient also from an economic point of view if compared to coal and diesel boilers. Currently, solar-hydrogen in fuel cells is already a good alternative for the replacement of old boilers supplied by gasoline/diesel or coal. The position of solar hydrogen is still worse than methane because condensation boilers and boilers equipped with burner with low combustion temperatures are largely improved.
Conclusions
• In a short period the liveability of the cities could be improved by replacing the current fuels employed in heating systems. In order to reduce the pollution related to the sulphur oxides and to the solid particulate, obsolete centralized plants supplied by diesel oil can be replaced by modern methane boilers. The exploitation of condensing boilers will allow also the reduction of nitrogen oxides, and the employment of electric heating systems, from a thermodynamic point of view, can appear competitive if compared with obsolete heating plants.
• Solar hydrogen represents an adequate alternative to traditional fuels, by waiting their depletion. An exploitation in a short period is achievable in appropriate boilers, in fuel cells or by mixing it with traditional fuels. The methane pipeline could be used for its transportation, but still several problems have to be solved. Actually, the obstacles to the hydrogen diffusion are not technical, but especially political and financial.
• The comparison carried out among the investigated fuels shows a net supremacy of solar hydrogen in term of environmental pollution if employed in fuel cells. The hydrogen global score decreases strongly if the safety index linked to its expansiveness characteristics is included.
• With reference to the safety aspects, fossil fuels appear still more suitable than hydrogen. In particular, by considering the expansiveness properties, hydrogen occupies the last position while with reference to the flammable properties it presents the highest score but very close to the methane and coal.
• From the point of view of the global impact index, hydrogen presents the worst score but it is no far for the score obtained for diesel boilers.
• In order to consider the solar hydrogen economically convenient as energetic option in the residential sectors, the evaluation of the global costs must include also the ones related to the final uses and to the effects linked to these uses. In this way, the higher price of hydrogen is compensated by almost null costs related to the environmental damages. Currently, considering the global costs, solar hydrogen in fuel cells results more competitive than coal and diesel burned in heating boilers.
The proposed index of environmental impact can be used from designers and citizens as a simple tool to quantify the produced pollution and the combustion control related to heating systems. It can be used also from public administrations in the investigation on the urban pollution produced by heating systems or from other sources.
References
- Nicoletti G(2001) L’impatto ambientale dei combustibili generalmente impiegati per il riscaldamento urbano degli edifici. 56° National Conference ATI (Italian Thermotechnic association).
- Enea B(2004)Sustainble development: Hydrogen: energy for the future. Center for Nuclear Science and Technology Information of the American Nuclear Society.
- Sheer H, Sonne DG (1987) Wassersfall Als Losung des Energie und Uniwelt Problems.
- Grubb M, Edmonds J, Brink PT, Morrison M (1993) The Costs of Limiting Fossil-Fuel CO2 Emissions: A Survey and Analysis. Annual Review of Energy and the Environment 18: 397-478.
- Seinfeld JH, Pandis SN (2012) Atmospheric Chemistry and Physics: From Air Pollution to Climate Change. (2ndedn), Wiley.
- Holgate ST(1999) Air Pollution and Health. Academic Press.
- Nicoletti G, Alitto G, Anile F (2009) Il Controllo della CO2: Misure e Strategie. Italian conference ATI, L’Aquila.
- Olesen BW(2004) International standards for the indoor environment.Indoor Air. 14: 12-16.
- IPCC(2001) Climate Change. Synthesis Report, Cambridge University, Press, New York.
- Kim HH (1992)Urban heat island. International Journal of Remote Sensing 13.
- Nicoletti G(1995) Hydrogen as Solar Energy Storage - Technical and Economical Aspects. Int. CongressHypothesis, Cassino.
- Barreto L, MakihiraA, Riahi K (2003)The hydrogen economy in the 21st century: a sustainable development scenario 28: 267-284.
- Boling B,Kheshgi H(2001) On strategies for reducing greenhouse gas emissions, Proceed. Nat. Ac. Sci 98: 4850-4854.
- Bevilacqua P, Coma J, Pérez G, Chocarro C, Juárez A (2015) Plant cover and floristic composition effect on thermal behavior of extensive green roofs. Building and Environment 92: 305–316.
- Nicoletti G(1995) The Hydrogen option for energy: a review of technical, environmental and economic aspects.Int J Hydrogen Energy 20.
- https://www.energy.eu
- NRC (National Research Council)(2004) The hydrogen economy: opportunities, costs, barriers, and R&D needs. National Academies Press.
- Nicoletti G (1994) Inquinamento Atmosferico da Combustione: Un approccio Termodinamico. La Termotecnica 9.
- D’Elia M, Bencardino L, Ciancarella M,Contaldi GV(2009) Technical and Non-Technical Measures for air pollution emission reduction: The integrated assessment of the regional Air Quality Management Plans through the Italian national model. Atmospheric Environment 43: 6182–6189.
- Nicoletti G, Alitto G, Anile F (2009) I Controllo della CO2: Misure e Strategie, Atti del convegno "ATI Aquila.
- Quadrelli R, Peterson S(2007) The energy-climate challenge: Recent trends in CO2 emissions from fuel combustion. Energy Policy 35.
- Dunn S(2002) Hydrogen futures: toward a sustainable energy system. Int. J. Hydrogen Energy.
- Cavallini A, Col DD (2011) Idrogeno Come Vettore Energetico. Energia e Fonti Rinnovabili, CSGI-IENI, Dip. Chimica, Università degli Studi di Pavia.
- Solomon BD, Banerjeeb A(2006) A global survey of hydrogen energy research, development and policy. Energy Policy 34.
- Momirlan M, Veziroglu TN (2002) Current status of hydrogen energy. Renewable and Sustainable Energy Reviews 6: 141-179.
- Veziroglu TN(1997) Hydrogen movement and the next action: fossil fuels industry and sustainable economics. Int J Hydrogen Energy 22.
- Feldman D, Barbose G, Margolis R, James T, Weaver S (2014) Photovoltaic System:Pricing Trends, Historical, Recent, and Near-Term Projections. NREL.
- www.nrel.gov/docs/fy08osti/41589.pdf
- www.autorita.energia.it/
- Mayer H(1999) Air pollution in cities. Atmospheric Environment 33: 4029-4037.
- Arienti R, Nicoletti G, Buttiglieri M(1990) Quality indices of hydrogen and other fuels. Ninth International Heat Transfer Conference, Jerusalem, Israel.
- Abdel-Aal HK, Sadik M, Bassyouni M, Shalabi M(2005) A new approach to utilize Hydrogen as a safe fuel. Int. J. Hydrogen Energy 30.
- Nicoletti G, Arcuri N, Nicoletti G, Bruno R (2015) A technical and environmental comparison between hydrogen and some fossil fuels. Energy Conversion and Management 89: 205-213.
- Chilton P (1973) Chemical Engineering: Handbook. McGraw Hill.
- Hidden Costs of Energy: Unpriced Consequences of Energy Production and Use (2010) The National Academies Press.
- Lvovsky K, Hughes G, Maddison D, Ostro B, Pearce D (2010) Environmental costs of fossil fuels: a rapid assessment method with application to six cities.Documents and Reports.
- De Paepe M, D’Herdt P, Martens D (2006) Micro-CHP systems for residential applications. Energy Convers Manage 47: 3435-3446.
- (2013)MEP/EEA air pollutant emission inventory guidebook: Technical guidance to prepare national emission inventories. European Environmental Agency.
Relevant Topics
Recommended Journals
- Oil & Gas Research Journal
- Renewable Energy and Applications Journal
- Oceanography Journal
- Industrial Pollution Control Journal
- Coastal Zone Management Journal
- Climatology & Weather Forecasting Journal
- Geoinformatics & Geostatistics Journal
- Engineering and Technology Journal
- Petroleum & Environmental Biotechnology Journal
- Polymer Sciences Journal
Article Tools
Article Usage
- Total views: 14901
- [From(publication date):
December-2015 - Aug 19, 2025] - Breakdown by view type
- HTML page views : 10300
- PDF downloads : 4601