Make the best use of Scientific Research and information from our 700+ peer reviewed, Open Access Journals that operates with the help of 50,000+ Editorial Board Members and esteemed reviewers and 1000+ Scientific associations in Medical, Clinical, Pharmaceutical, Engineering, Technology and Management Fields.
Meet Inspiring Speakers and Experts at our 3000+ Global Conferenceseries Events with over 600+ Conferences, 1200+ Symposiums and 1200+ Workshops on Medical, Pharma, Engineering, Science, Technology and Business
Review Article Open Access
Co-contraction Role on Human Motor Control. A Neural Basis
| Marlene Rosa* | |
| Autonomous Unit of Health Sciences, University of Aveiro, Portugal | |
| Corresponding Author : | Marlene Rosa Autonomous Unit of Health Sciences University of Aveiro, Portugal Tel: 35-1968918915 E-mail: marlenerosa@ua.pt |
| Received: November 13, 2014; Accepted: February, 2015; Published: February 9, 2015 | |
| Citation: Rosa M (2015) Co-contraction Role on Human Motor Control. A Neural Basis. J Nov Physiother 5:248. doi: 10.4172/2165-7025.1000248 | |
| Copyright: © 2015 Marlene Rosa. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. | |
Visit for more related articles at Journal of Novel Physiotherapies
Abstract
The aim of this overview is to understand the role of the co-contraction on movement accuracy and the respective neural processes involved in healthy people and in subjects after a Central Nervous System Lesion (CNS). First, it will be discussed the relevance of co-contraction to the motor control, based on Internal Model Theory and Equilibrium Point Theory. Secondly, it will be discussed the muscle co-contraction neural regulation at a spinal level control and how the agonist-antagonist muscles work on healthy and neurologic impairment subjects.
Figures at a glance
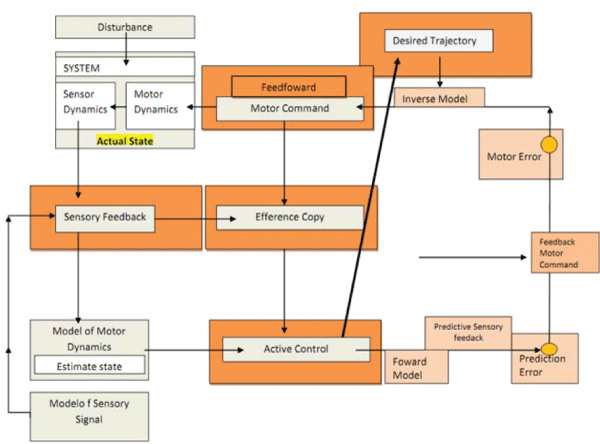 |
 |
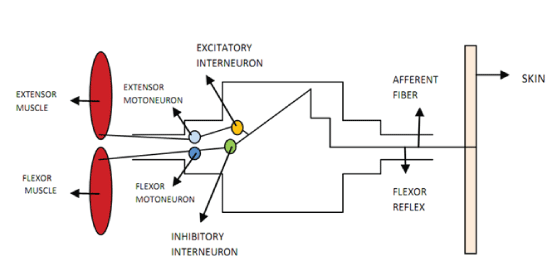 |
| Figure 1 | Figure 2 | Figure 3 |
Post your comment
Relevant Topics
- Electrical stimulation
- High Intensity Exercise
- Muscle Movements
- Musculoskeletal Physical Therapy
- Musculoskeletal Physiotherapy
- Neurophysiotherapy
- Neuroplasticity
- Neuropsychiatric drugs
- Physical Activity
- Physical Fitness
- Physical Medicine
- Physical Therapy
- Precision Rehabilitation
- Scapular Mobilization
- Sleep Disorders
- Sports and Physical Activity
- Sports Physical Therapy
Recommended Journals
Article Tools
Article Usage
- Total views: 19372
- [From(publication date):
February-2015 - Aug 29, 2025] - Breakdown by view type
- HTML page views : 14519
- PDF downloads : 4853
