Research Article Open Access
Combined Pharmacokinetic Model for Lacosamide and its Main Metabolitefor Integrated Pharmacokinetic Modeling in Humans
| Carina Schaefer1,2 and Willi Cawello1* | |
| 1UCB Pharma, Monheim, Germany | |
| 2University of Düsseldorf, Institute Clinical Pharmacy and Pharmacotherapy, Düsseldorf, Germany | |
| Corresponding Author : | Willi Cawello UCB Pharma, Alfred Nobel Str. D40789 Monheim am Rhein, Germany Tel: (+49) 2173 481480 Fax: (+49) 2173 481947 E-mail: Willi.Cawello@ucb.com |
| Received: September 30, 2015; Accepted:January 12, 2015 Published: November 22, 2015 | |
| Citation: Schaefer C, Cawello W (2015) Combined Pharmacokinetic Model for Lacosamide and its Main Metabolite for Integrated Pharmacokinetic Modeling in Humans. J Pharmacokinet Exp Ther 1:101. doi:10.4172/jpet.1000101 | |
| Copyright: ©2015 Schaefer C, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. | |
| Related article at Pubmed, Scholar Google | |
Visit for more related articles at Journal of Pharmacokinetics & Experimental Therapeutics
Abstract
Pharmacokinetic (PK) modeling and simulation are fundamental to describe a drug’s fate in a biological system. An understanding of therapeutically effective drug concentrations, dose-related adverse events and appropriate dosing schedules can be informed by PK. Combined PK models that include the model-dependent PKs of a drug and its metabolites in plasma and unchanged drug in urine broadens the spectrum of separated PK models. Software used for PK modeling was validated and evaluated by simulating concentration-time data of a fictive study population. Results of precision and accuracy were under 15% and met criteria for bioanalytical method validation. The PK model was applied to lacosamide and its main metabolite in plasma and lacosamide excreted in urine of healthy subjects and subjects with mild-to-severe renal impairment of a Phase I trial. Resulting PK parameters were consistent with the present understanding of the dependence between lacosamide’s metabolism and renal excretion and behavior in plasma. A model-independent analysis showed elimination processes consisted of renal and metabolic elimination, whereas renal elimination was dependent and metabolic elimination independent from renal function. The developed PK model represents progress in understanding the dependence of lacosamide’s renal excretion and the independence of lacosamide’s metabolism on renal function as well as its behavior in healthy subjects as well as in subjects with normal and impaired renal function.
| Keywords |
| Elimination; Lacosamide; Metabolite kinetics; Mathematical models; Pharmacokinetic; Renal clearance |
| Introduction |
| Pharmacokinetic (PK) modeling and simulation allows integration of data to inform appropriate dose selection and dosing schedules, which are critical aspects of clinical drug development [1,2]. A PK model based on the analysis of concentration-time data and including individual patient characteristics is necessary to transform drug dose into concentrations that can be used in individualized therapy regimens [3]. Development of the mathematical context of a drug concentration in different tissues and body fluids provides an understanding of doserelated adverse events (e.g., toxic effects) and informs on the effective concentrations in plasma [4]. |
| Although several PK text books describe the model-dependent PK of a drug in a tissue (e.g., drug in plasma or excreted in urine) to reflect the complex mechanisms of transport processes, it is important to develop new models that include the model-dependent PKs of a drug and its metabolites in plasma and of unchanged drug in urine. Several physiological and pathological processes such as impairment of renal or hepatic function can lead to alterations in the PK profile of a drug and its metabolites, requiring adaptions of standard dosing regimens [5]. The development of a PK model that accurately describes the kinetics of a drug and its metabolites through the body, including the amount excreted in urine, could permit the calculation of relevant PK parameters from given concentrations in plasma and amounts in urine. PK parameters serve as the connection between the three mentioned models (i.e., PKs of drug and metabolite in plasma and drug excreted in urine) due to overlap of some PK parameters between the models. Exploiting this connection could yield progress in understanding different drug concentration-time curves in plasma and drug exposures in subjects with different medical conditions such as renal impairment |
| In this paper, we illustrate this approach with lacosamide, a newer antiepileptic drug (AED) that selectively enhances the slow inactivation of voltage-gated sodium channels, which has been approved (in doses of up to 400 mg/day) for the treatment of focal seizures in adults as monotherapy (USA only) or adjunctive therapy (US, EU and other countries) [6,7]. Well-controlled, double-blind trials in adults with partial-onset seizures have demonstrated the efficacy and safety of lacosamide as adjunctive therapy [8-10] and as conversion to lacosamide monotherapy [11]. A 1-year, prospective study reflecting clinical practice suggested that conversion to lacosamide monotherapy could be effective and well tolerated in selected adults patients with partial onset seizures who had achieved seizure freedom during lacosamide add-on therapy [12]. |
| Lacosamide shows dose-proportional PKs after single dose (100– 800 mg) oral administration and has no first pass effect [5-7]. Plasma protein binding is below 15% and the terminal half-life is about 13 h [5-7]. Steady-state plasma levels can be achieved within 3 days after dose initiation [13]. Lacosamide elimination occurs mainly via the kidneys (95%), with 40% as unchanged drug, ~ 30% as the inactive O-desmethyl metabolite, ~ 20% as a polar fraction, and the rest as additional metabolites [14]. The volume of distribution, Vd, is 0.6 L/ kg and corresponds nearly to total body water [15]. Furthermore, lacosamide does not interact with commonly used AEDs [16,17]. An adequate PK model that is able to fit lacosamide data, and simulate and predict various case scenarios, could provide an improved understanding of the behavior of the drug in individual subjects. Moreover, appropriate mathematical models should lead to a better understanding of the relationship between the PK parameters of the parent drug its metabolism and excretion. The model developed for lacosamide may also provide a basis for PK modeling with other drugs. |
| The software was validated for its suitability for PK modeling by iterating the values for the PK parameter on the basis of the models. The results of validation were evaluated statistically. The suitability of the developed system of PK models was also evaluated with lacosamide study data in healthy subjects and subjects with renal impairment. |
| Method |
| Development of PK models |
| The system of PK models developed was designed to predict the behavior of |
| 1. unchanged drug in plasma, |
| 2. the main metabolite in plasma, and |
| 3. unchanged drug excreted in urine. |
| The model should later be used for pharmacokinetic modeling with lacosamide which means that the model should be able to predict, as mentioned before, the behavior of lacosamide in plasma, the main metabolite, O-desmethyl-lacosamide in plasma, and unchanged lacosamide excreted in urine. The mathematical PK models were evaluated using the convolution method described by Benet and Turi [18] to develop Laplace equations for the amount of drug in the central compartment by a simple multiplication of the input and disposition functions. The input function is used to describe the route of administration whereas the disposition function describes the first order distribution and elimination processes. For the disposition function, a one-compartment model was used. |
| Figure 1 illustrates the amounts of drug (D) and its main metabolite (M) in the central compartment showing drug absorption, metabolism and renal elimination, as well as renal elimination of the main metabolite. Ud and Um represent the amount of unchanged drug and metabolite in urine. The rate constant of drug absorption is represented by ka. The overall rate constant of elimination, ke, should be the sum of renal excretion (characterized by rate constant kren), metabolism and other elimination processes. The rate constant of creation of the main metabolite is denoted by km, [19] while kme represents the rate constant of elimination of the metabolite. |
| While the mathematical model for PK of a drug after oral administration was represented by the Bateman function, Laplace equations were generated for the plasma concentration of the metabolite and the amount of unchanged drug excreted in urine. To derive the equation describing metabolite concentration over-time profile, the fingerprint method was used for back-transformation of the generated Laplace equation [18]. The volume of distribution of unchanged drug (Vd) and of the metabolite (Vdm) served as scaling factors to connect the concentrations of unchanged drug and metabolite in plasma and were included in the mathematical model. |
| In the validation process, the equations for the model-dependent PK of unchanged drug in plasma and its renal excretion, as well as the PK of the main metabolite in plasma, were connected to a system of equations in order to use all data from given datasets and connect the PK parameters of each model into one system for evaluation. |
| Software and data |
| The present evaluation used SAS version 9.3 to generate randomized values of PK parameters and to calculate the concentration of a drug and its main metabolite in plasma and the amount of unchanged drug in urine from 20 subjects of a fictive generated study population in SAS. Using the nlin procedure in SAS, the developed system of equations was validated with data from the fictive study population and then used for PK modeling, using actual patient plasma and urine data from a Phase I trial of lacosamide in subjects with and without renal impairment [13]. |
| Validation |
| Data generation for the fictive study population: To validate the used tools, functions were chosen that described the drug and metabolite concentrations in plasma-over-time profiles and amount of drug excreted in urine. The values of the PK parameters for each fictive subject were randomized with a normal distributed variability in order to reflect inter-individual variability. The rannor function in SAS was used to provide randomized normal distributed values. Table 1 presents mean values of the generated PK parameters and their standard deviations (SD) from a generated fictive study population of 20 subjects. |
| On the basis of the random values of the PK parameters and mathematical models, data sets of the concentration-time profiles in plasma or the amount excreted at defined time points were calculated. The sampling time points after drug administration were 0.25, 0.5, 0.75, 1, 1.5, 2, 4, 6, 8, 12, 16, 24, and 48 hours for the unchanged drug in plasma, and same time points plus 36, 72, 96 and 120 hours for the metabolite in plasma. For urine data, the time intervals for sampling were 0–2, 2–4, 4–6, 6–8, 8–12, 12–16, 16–24, 24–36, 36–48 and 48–72 hours. |
| Generation of concentration data of the fictive study population: With the generated fictive pharmacokinetic parameters of all 20 subjects, the mathematical models were used to calculate the concentration of unchanged drug and metabolite in plasma as well as the amount excreted in urine for each subject by inserting the individual values of PK parameters at each sampling point or end of the collection interval (for urine data) at time, t. A total of 13 time points representing blood samples, 17 time points representing metabolite sampling, and 10 time points representing urine sampling were chosen as representative points of time for sampling (as specified above). |
| Calculated plasma concentrations and amounts excreted in urine were assigned a proportional error to imitate typical errors associated with analyzing processes for drug concentrations or amounts excreted in urine. For this step, the rannor function was used to generate random numbers following a normal distribution around zero with a SD of 0.1. |
| PK modeling |
| The non-linear regression model in SAS was used to estimate individual PK parameters of each subject from a set of concentration data values. Using the Marquardt method, the nlin procedure works with an iteration process evaluated by the minimized sum of squares for differences between generated and predicted concentrations or amounts. The sum of squares of the predicted concentrations was weighted with a weight command that considers not the absolute but the relative error. The weighting procedure was executed by the method 1/(reference value)2. |
| Simulation and correlation: With the predicted values of PK parameters, concentration-over-time profiles for unchanged drug and metabolite in plasma and for cumulative amount excreted in urine for each subject were calculated in the validation process. |
| To demonstrate the correlation between predicted and reference PK parameters as well as between concentration values or amounts excreted in urine and the corresponding reference values, each correlation was illustrated by a regression line. Results of regression were defined by the parameters of intercept and slope. Correlation was expressed through the coefficient of correlation by using the reg procedure in SAS. |
| PK modeling with sp0641 study data |
| Study design and population: Study SP0641 was an open-label, single lacosamide dose, Phase I trial (NCT01796938) [5]. The trial was conducted in accordance with the Declaration of Helsinki, the local laws of the country involved, and the ICH Tripartite Guideline (Guideline for Good Clinical Practice, May 1996). The study was a sequential group comparison to investigate the PK, safety, and tolerability of 100 mg lacosamide in subjects with different degree of renal impairment (mild, moderate, severe), including those requiring dialysis, compared with healthy subjects following a single oral dose [5]. The study population was Caucasian male and female adults (aged 18–70 years) with a body mass index of 20–34 kg/m2. |
| Participants were allocated to one of four groups based on their creatinine clearance (CLCR), determined according to Cockcroft-Gault: Healthy controls (CLCR ≥ 80 mL/min); mild renal impaired subjects (80 mL/min ≥ CLCR ≥ 50 mL/min); moderate renal impaired subjects (50 mL/min ≥ CLCR ≥ 30 mL/min); and severe renal impaired subjects (CLCR of 20–30 mL/min or CLCR<20 mL/min) [5]. None of the severe renal impaired subjects was on hemodialysis 2 weeks prior to or during the trial [5]. Each group consisted of 8 subjects. The subjects with with end-stage renal disease were not included in the present analysis because urine data was unavailable due to dialysis. |
| Treatment and sample collection: Among participants in Groups 1–4, single blood and urine samples were collected pre dose, and then a single oral dose of 100 mg lacosamide was administered on day 1. Lacosamide and O-desmethyl-lacosamide concentrations in samples from human plasma and urine have been determined using a high performance liquid chromatography–tandem mass spectrometry method The PK of lacosamide and its main metabolite in plasma were assessed 0.5, 1, 1.5, 2, 3, 4, 6, 8, 12, 24, 36, 48, 60, 72, 84, and 96 h after lacosamide administration. The validated lower limit of quantification for both lacosamide and the O-desmethyl metabolite in plasma was 0.01 μg/mL. The calibration range was 0.01–10 μg/mL for lacosamide and 0.01–5.0 μg/mL for the main metabolite in plasma. Precision was 0.2–6.3% for lacosamide and 0.7–6.5% for the metabolite whereas accuracy was 96.4–107.4% and 97.6–102.6%, respectively. |
| Urine samples for the determination of renal excretion of lacosamide and its main metabolite were collected 0–4, 4–8, 8–12, 12– 24, 26–36, and 36–48 h post dose. The calibration range was 0.2–200 μg/mL; precision was 0.8–3.7% for lacosamide and 0.3–4.3% for the main metabolite. Accuracy was 88.3–108.3% for lacosamide and 93.4– 103.0% for the metabolite. |
| PK modeling process: Because the study included healthy subjects as well as subjects with renal impairment, it was considered important to include individual start parameters in the modeling process in order to achieve better iteration results. Based on the evaluation of Cawello et al., [5] estimations for kren and km can be made using the known CLCR derived from ke. From the expected dependence between kme and CLCR, the starting parameters for iteration of kme can be determined. Recent validations have shown that, due to fewer sampling points in the absorption phase, the iteration process for ka could be imprecise. For that reason, ka was fixed for each individual subject, with that value taken from recent PK modeling with SP0641 data (using the Bateman function). |
| Statistics |
| Statistics of validation process in SAS: To evaluate the adequacy of the SAS nlin procedure, typical validation characteristics (e.g., accuracy and precision) of PK parameters were evaluated as follows: |
| Error = Valreference – Valiterated |
| Relative error (%) = Error/Valreference × 100 |
| Accuracy (%) = mean (relative error) |
| Precision (%) = SD of relative error |
| with Valreference=reference value and Valiterated=iterated value of PK parameter. |
| Accuracy and precision were chosen as desired statistical measures for evaluation, as is proposed in the ICH Harmonised Tripartite Guideline of validation of analytical procedures [20], and were evaluated in light of the US Food and Drug Administration (FDA) guideline for bioanalytical method validation [21]. While the FDA states a replicate of samples or measurements are needed for these determinations, our evaluation is based on the precision and accuracy of iterated values compared with measured or generated values of the individual subjects of a fictive study population. The mean value of accuracy should be within 15% of the actual value and the precision at each concentration level should not exceed 15% of the coefficient of variation [21]. |
| Descriptive statistics were used to calculate precision and accuracy. The statistics for each PK parameter, as well as individual differences between values of iterated PK parameter and corresponding reference value of PK parameter, included arithmetic mean, SD and range (minimum, maximum), were calculated with the SAS summary procedure. |
| Statistics of PK modeling results with SP0641 study data: PK parameters developed in SAS through iteration processes were evaluated by descriptive statistics. For Vd, Vdm, kren, km, and kme, arithmetic means with corresponding SD were calculated. Median was used as an appropriate point estimate for absorption lag time (tlag), and range was determined for all PK parameters. During the iteration process, the weighted least square was used to estimate the best fit when analyzing data and finding the parameter values. |
| The regression analysis was performed for the correlation between measured and predicted concentrations/amounts as well as for the correlation between CLCR and kme, kren and km. The regression analysis was evaluated by calculating the coefficient of determination, along with the line parameters of intercept and slope. |
| Results |
| Mathematical PK models |
| The following equations are the result of the back-transformation of generated Laplace equations for description of drug and metabolite transports after oral administration in central circulation as well as renal elimination of unchanged drug. F represents relative bioavailability (F is set as 1 for a 100% bioavailability) and D represents dose. |
| 1. Unchanged drug in plasma (Bateman function) |
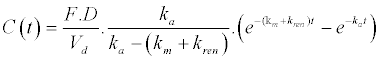 |
| 2. Unchanged drug excreted in urine |
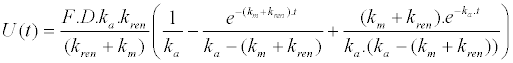 |
| 3. Metabolite in plasma |
| y = ti.dr.C(t) − (ti−1).dr.U(t) − ti.(dr−1).Cmet(t) |
| Validation |
| The concentration of unchanged drug (dr=1) and metabolite (dr=0) in plasma (ti=1) and the cumulative amount of unchanged drug excreted at time, t, in urine (ti=0) is described by the following equation: |
| y = ti.dr.C(t) − (ti−1).dr.U(t) − ti.(dr−1).Cmet(t) |
| where ti and dr are used to connect the three mathematical models. |
| PK parameters Vd and Vdm were determined with an accuracy of 0.57 and −0.26%, and a precision of 3.2 and 5.21%, respectively. The rate constants ka, kme, km and kren were determined with an accuracy of 0.97, −0.03, −0.40 and −0.53%, and a precision of 8.68, 4.89, 3.74 and 3.53%, respectively. Table 2 presents the results of regression analysis between reference and predicted concentrations of unchanged drug in plasma, metabolite in plasma and cumulative amount of unchanged drug in urine, as well as between reference and predicted PK parameters. |
| Evaluation with SP0641 study data |
| The SP0641 study population consisted of male and female subjects aged between 25 and 68 years (Table 3). Further demographic parameters, including CLCR are listed in Table 3. |
| The range of ka resulting from PK modeling with the Bateman function was between 2.249 and 10.0 h−1 with an arithmetic mean of 8.884 h−1 and a SD of 2.490 h−1. It should be noted that iteration of ka was restricted by an upper limit of 10 h−1. Thus, the value 10 h−1 should not be seen as the actual iterated value. Means and SD of other PK parameters are provided in Table 4. |
| The correlation of measured lacosamide concentrations in plasma with predicted concentrations was 0.9697, with an intercept of 0.0585 and slope of 0.9230 (Figure 2a). Regression analysis of predicted and measured concentrations of the main metabolite in plasma revealed characteristics of a strong correlation between measured and predicted concentrations (i.e., coefficient of determination, 0.9772; intercept, −0.4676; slope, 1.0364; Figure 2b). The same was true for the comparison between predicted and measured amounts of unchanged drug in urine (coefficient of determination, 0.9758; slope, 1.0784; intercept, −0.0120; Figure 2c). |
| It is assumed that the elimination rate constant consists of the sum of renal excretion and metabolism and could be replaced by the sum of PK parameters km and krem. In order to illustrate in how far rate constants of elimination kren and kme and rate constant of metabolism are dependent or independent on renal function (expressed as CLCR), kren, kme and km were correlated with CLCR (Figure 3). kren and kme both showed a tendence of correlation with CLCR as the coefficients of determinations were 0.6799 for kren and 0.3488 for kme. km showed no dependence on renal function as the coefficient of correlation was 0.03. |
| A further correlation was examined between Vd and body height with a coefficient of determination of 0.7051, because of the reason that Vd is associated with total body water and increasing muscle mass mostly consists of water (Figure 4). |
| Discussion |
| In the present post hoc evaluation, a general PK model was developed to describe the PKs of unchanged drug in plasma, unchanged drug excreted in urine, and the main metabolite in plasma. Furthermore it could be shown that the developed system of PK models can be used for PK modelings with lacosamide in healthy subjects and subjects with mild to severe renal impairment. The procedure nlin used in SAS was shown to be an adequate tool for PK modeling with a developed system of mathematical models and with study data of lacosamide and its main metabolite in healthy subjects and subjects with renal impairment. In the literature, model-dependent PKs of a drug are described [22]. Nevertheless, the development of a PK model that combines the modeldependent PK of unchanged drug in plasma and urine as well as the PK of its metabolite represents progress in the evaluation of modeldependent PKs. The model was successfully developed from a given set of Laplace equations via back-transformation. Moreover, it was shown that the model could be used for PK modeling in subjects with and without renal impairment. |
| The validation analysis of the nlin procedure with a fictive study population demonstrated that the procedure worked well for PK modeling. SAS and other software packages such as NONMEM, Kinetica, WinNonlin and Topfit have already been evaluated as adequate tools for evaluation of correct values for PK parameters [22,23]. Nevertheless, the AGAH Working Group used the Gauss- Newton algorithm of iteration and concentrated on the description of single systems, whereas the present analysis is based on the Marquardt algorithm and considers the combination of the three systems for the first time. The analysis in SAS resulted in accuracy and precision values for PK parameters that were under 10% and therefore met the criteria of the guidance level of the FDA. A strong linear relationship was observed for all PK parameters (with coefficients of determination around 0.9–1.0 except for ka with a value of around 0.5) as well as for the concentrations of unchanged drug and metabolite in plasma and amounts excreted in urine. |
| The validation of the nlin procedure to evaluate mathematical PK models employed a fictive study population generated in SAS. The questions of interest included 1) whether the model could be used for PK modeling using lacosamide concentrations in plasma and in urine of healthy subjects and subjects with mild to severe renal impairment, and 2) whether predicted PK parameters would reflect current understanding of how developed PK parameters change within populations because of renal impairment in different stages. It is known that lacosamide is predominantly eliminated from the systemic circulation via the kidneys and via the liver through biotransformation [15]. Renal impairment can lead to alterations in the PK profile of drugs and their metabolites, reflected in a decrease in renal excretion or metabolism [5]. Although lacosamide does not require dose adjustment based on age, sex or in subjects with mild-to-moderate renal impairment, it was of interest to ascertain if the developed PK model could be used for these mentioned populations [5,24]. Regarding the regression analysis of predicted and measured concentration/amounts (Figures 2a-2c) it could be shown that there is a good correlation between measured and predicted values because of coefficient of determination values near 1. The correlation between measured and predicted concentrations of lacosamide in plasma (Figure 2a) showed some points that lie apart from the regression line, which may be traced back to the fast absorption of lacosamide after oral administration. Because distribution processes have not been completed, a two-compartment model could be expected for lacosamide until it has been distributed finally between blood (central compartment) and peripheral compartments. The rate constant of elimination of an orally-administered drug consists of the sum of kren and km. The work of Cawello et al. [5] has already shown a possible correlation between renal, metabolic and total clearance versus renal function following a model-independent analysis of PK parameters. Metabolic clearance was shown to be a prominent component of total body clearance (>60% of total clearance in healthy subjects) [5]. For that reason, ke was replaced by the sum of km and kren to consider both processes in parallel. The assumption that kren and kme are dependent on renal function (expressed as CLCR) could be confirmed when correlating kren and kme with CLCR (Figure 3). Both correlations showed dependence of rate of elimination on renal function. Because around 34% of lacosamide is eliminated as the O-desmethyl metabolite, it could be assumed that km would not be affected by renal impairment. This fact was confirmed by the lack of correlation between km and CLCR (Figure 3). Indeed, the regression line was nearly parallel to the x-axis with values constantly fluctuating between 0.02 and 0.05 h-1. |
| The Vd of lacosamide is approximately 0.6 L/kg and therefore close to that of total body water [7,15]. Total body water usually decreases with advancing age [25] but can increase with increasing muscle mass, which mostly consists of water. Therefore a correlation is expected between Vd and body height. Schaefer et al. [24] showed that the Vd calculated for each individual subject (using an empiric equation accounting for gender, body weight, height, and age) involved a scaling factor to describe differences in lacosamide plasma concentrations in healthy subjects of different age and gender [24]. Figure 4 illustrates the correlation between iterated Vd after a model-dependent PK of each individual subject and the measured body height in centimeters. The coefficient of determination was 0.7051 and confirmed the expected relationship between body height and Vd. The variability might be explained by the fact that an increase in body height may be associated with an increase in muscle or body fat. Because body fat has a lower water content than muscle, it would not increase the Vd. Schaefer et al., [24] have found that women in general had a lower Vd because of higher body fat in contrast to men. A lower Vd explained the numerically higher lacosamide plasma concentrations measured in women than in men. Nevertheless, the demonstrated correlation between Vd and body height support the finding that the PK model described here could also be used for PK modeling in subjects with renal impairment and with different body composition. |
| Conclusion |
| The present analysis included the development of a new combined PK model that describes the model-dependent PK of unchanged drug in plasma and in urine as well as its metabolite in plasma. Moreover, the PK model was applied to lacosamide and to the main metabolite plasma concentrations as well as lacosamide amounts excreted in urine of healthy subjects and subjects with mild-to-severe renal impairment of a Phase I trial. The PK parameters were consistent with our present understanding of the drug’s behavior in this population and leads to a better understanding of the effect of renal function on the renal excretion of lacosamide and its main metabolite and also of the independence between renal function and lacosamide’s metabolism. The new model separates elimination of lacosamide after oral administration into renal elimination and elimination via metabolism. Because of the link of three PK models (transports of unchanged drug in plasma, transport of unchanged drug into urine, and transports of main metabolite in plasma) with the overlapping of PK parameters included in the three PK models, a more precise picture of all transport processes could be shown. |
| The results of this PK modeling study reveal progress in the understanding of lacosamide’s behavior in healthy subjects, subjects with impaired renal function and subjects with different body compositions. When applied to other drugs, this PK modeling approach could be considered to better understand the PK behavior of drugs and their metabolites in different patient populations. |
| Acknowledgements |
| The SP641 study included was funded by UCB Pharma (Brussels, Belgium). Writing support was provided by Lynne Isbell, PhD, CMPP of Evidence Scientific Solutions, and was funded by UCB Pharma. The authors also acknowledge Barbara Pelgrims, PhD (UCB Pharma, Brussels, Belgium) for publication coordination. |
| Conflict of Interest |
| Carina Schaefer is an employee of the Heinrich-Heine-University of Düsseldorf and is supported in her PhD thesis about lacosamide pharmacokinetics by UCB Pharma. This project is collaboration between the Heinrich-Heine-University of Düsseldorf and UCB Pharma. |
References |
|
Relevant Topics
- Adalimumab Pharmacokinetics
- ADME Studies
- Atorvastatin Pharmacokinetics
- Clinical Pharmacokinetics
- Clopidogrel Pharmacokinetics
- DMPK Studies
- Esomeprazole Pharmacokinetics
- Etanercept Pharmacokinetics
- Fluticasone Pharmacokinetics
- Infliximab Pharmacokinetics
- Linear Pharmacokinetics
- Morphine Pharmacokinetics
- Nonlinear Pharmacokinetics
- Olanzapine Pharmacokinetics
- Pharmacokinetics Modelling
- Quetiapine Pharmacokinetics
- Rosuvastatin Pharmacokinetics
Recommended Journals
Article Tools
Article Usage
- Total views: 12151
- [From(publication date):
May-2016 - Aug 30, 2025] - Breakdown by view type
- HTML page views : 11101
- PDF downloads : 1050
