Review Article Open Access
GATES as the Unique Tool for Simulation of Electrolytic Redox and Non-Redox Systems
Anna Maria Michalowska-Kaczmarczyk1 and Tadeusz Michalowski2*
1Department of Oncology, The University Hospital in Cracow, Poland
2Faculty of Engineering and Chemical Technology, Technical University of Cracow, Poland
- *Corresponding Author:
- Tadeusz Michalowski
Faculty of Chemical Engineering and Technology
Cracow University of Technology
Warszawska 24, 31-155 Cracow, Poland
Tel: +48126282035
E-mail: michalot@o2.pl
Received date: August 14, 2014; Accepted date: September 03, 2014; Published date: September 08, 2014
Citation: Michalowska-Kaczmarczyk AM, Michalowski T (2014) GATES as the Unique Tool for Simulation of Electrolytic Redox and Non-Redox Systems. J Anal Bioanal Tech 5:204 doi: 10.4172/2155-9872.1000204
Copyright: © 2014 Michalowska-Kaczmarczyk AM, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited
Visit for more related articles at Journal of Analytical & Bioanalytical Techniques
Abstract
The Generalized Approach to Electrolytic Systems (GATES), based on physical (charge conservation), physicochemical (conservation of elements) and chemical (mass action) laws is the best theory applicable for computer simulation of equilibrium, non-equilibrium and metastable, mono- and polyphase electrolytic redox and non-redox systems. The Generalized Electron Balance (GEB) concept, related to electrolytic redox systems, is put in context with the principle of conservation of all elements in electrolytic redox systems, with aqueous, non-aqueous or mixedsolvent media. Two equivalent approaches to GEB are presented, and termed as the Approach I and Approach II to GEB. The GEB, that enters GATES as GATES/GEB, is fully compatible with charge and concentration balances and completes the set of equations necessary for thermodynamic resolution of redox systems. Computer simulation of such systems is based on all attainable physicochemical knowledge involved in the related algorithm, solvable with use of an iterative computer program, and then presented graphically. This paper is referred mainly to dynamic redox systems, realized according to titrimetric mode. The speciation diagrams for dynamic redox systems are perceived as a reasonable alternative to (static) Pourbaix diagrams. The GEB concept, unknown before 1992, is perceived as the law of the matter conservation, as the general law of Nature. From the GATES viewpoint, the stoichiometric reactions are only the basis to formulate the related equilibrium constants. GATES is also the basis for Generalized Equivalence Mass (GEM) concept, formulated with none relevance to the stoichiometry of chemical reaction notation. From the GATES viewpoint, the stoichiometry is a superfluous concept.
Keywords
Electrolytic systems; Redox equilibria; GEB; GATES
Introduction
Any electrolytic system is described with use of charge and material balances referred–in principle–to closed systems, separated from the environment by diathermal walls. The latter assumption enables any process occurred in the system to proceed under isothermal conditions. Constant temperature (T) is one of the conditions needed to secure constancy of equilibrium constants K=K(T, I) values [1-8]; I is the ionic strength of the solution. Constancy of I value can be secured in the system of isohydric solutions [9-12], without the necessity of application of a basal electrolyte.
The electrolytic systems are formed after introducing some solutes, into a solvent (considered as single substance) or a mixture of different solvents. Any system containing a mixture of two solvents forms a binary-solvent system [10,13], if the solvents are miscible at any mutual ratio. Two immiscible solvents form two separate phases in liquidliquid extraction systems [5,14,15].
The species in any electrolytic non-redox system are involved in charge and k concentration balances, referred to element(s) E(i)≠H, O, or to some clusters of atoms named as cores, involving these elements, E(i). In other words, charge and concentration balances, form a compatible set of k+1 equations needed for quantitative, algebraic description of non-redox systems. For redox systems, the new, compatible balance referred to electron transmission or distribution is needed. The principles of formulation of the k+2-th balance, known as the Generalized Electron Balance (GEB), were discovered by Michalowski, and presented as two equivalent Approaches: I [14,16- 24] and II [25-37] to GEB.
The Principles of Formulation of Approaches I and II to GEB
The Approach I to GEB is based on a “card game” principle, with electrons as “money”, electron-active elements as “players”, and electron-non-active elements as “fans”. In redox reactions, one (disproportionation, synproportionation) or more electron-active elements can be involved. The Approach I can be applied for any redox system, where oxidation numbers for all elements in the species present in it can easily be calculated.
The Approach II to GEB is based on the balance 2·f(O)–f(H), formulated for any redox system, as linear combination of the elemental balances: f(H) for H and f(O) for O, related to this system; it is named as the primary form of GEB, and denoted as pr-GEB=2·f(O)– f(H). The pr-GEB is linearly independent on other elemental/core balances and charge balance. All linear combinations of pr-GEB with other elemental/core balances and charge balance have full properties of GEB. For any non-redox system, 2·f(O)–f(H) is linearly dependent on charge and concentration balances. This independency/dependency criterion, valid for any redox/non redox systems, can be extended on mixed-solvent systems with amphiprotic and aprotic solvents involved, particularly on binary-solvent media [33,36], where acidbase properties of different solutes were tested [13,38].
The GEB is put in context with the Generalized Approach to Electrolytic Systems (GATES) [28] as GATES/GEB. The GATES relates to redox [14-37] and non-redox [39-43] systems of different complexity.
In all instances, the species 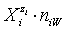 in the related solvents or mixtures of solvents are considered in their natural forms, i.e. as hydrates
in the related solvents or mixtures of solvents are considered in their natural forms, i.e. as hydrates 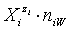 in aqueous (W=H2O) media, or as solvates
in aqueous (W=H2O) media, or as solvates 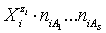 in mixture of S co-solvents, A1,…,AS, where at least one of the co-solvents should have amphiprotic properties; ni ≥ 0 is the mean number of water particles in
in mixture of S co-solvents, A1,…,AS, where at least one of the co-solvents should have amphiprotic properties; ni ≥ 0 is the mean number of water particles in 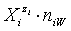 and
and 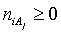 (j=1,…,S) in
(j=1,…,S) in 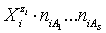
Although the Approach II is equivalent to the Approach I, it offers essential advantages. The great advantage of the Approach II is that none prior knowledge on oxidation numbers of elements in complex species of definite (known or pre-assumed) composition, expressed by its formula and external charge it needed, particularly when complex organic substances, e.g., plant pigments, participating redox reactions are considered [44-48]. It should be stressed that redox reaction are usually involved in other (acid-base, complexation, precipitation) types of chemical reactions. Redox reactions can also be related to liquidliquid extraction systems [14]. Within GATES/GEB, the terms: oxidant and reductant are not ascribed a priori to particular species. The Approach II to GEB is applicable, inter alia, for redox systems where radical and ion-radical species are formed, as ones stated in the systems with Fenton reagents involved [28], or in the systems where oscillation reactions occur [18,28].
For calculation purposes, the set of (charge, GEB and concentration) balances is completed by the set of relations for independent equilibrium constants, interrelating concentrations of some subsets of species involved in the balances. The complete set of equilibrium constants provides all quantitative knowledge on the system in question. Some qualitative knowledge is also valuable; this knowledge is particularly desired in the case of metastable systems. The calculations are made according to iterative computer programs, particularly ones offered by MATLAB [28]. The GATES/GEB refers to redox systems of any degree of complexity, mono- and polyphase systems. Any equlilibrium, metastable and non-equilibrium, static and dynamic systems can be tested this way, with none simplifying assumptions needed.
GATES and Generalized Equivalence Mass (GEM)
From the GATES viewpoint, the stoichiometric reactions are only the basis to formulate the related equilibrium constants. Stoichiometry of reactions is not a primary concept in chemistry, and its application provides frequently false/caricatural results. GATES is also the basis for Generalized Equivalence Mass (GEM) concept [27], formulated with none relevance to the stoichiometry of chemical reaction notation. The GEM is a simple consequence of elemental balances, and is not involved with a stoichiometry of the reaction notation. Then GEM contradicts the definition of equivalence “weight” concept, still obligatory according to IUPAC decision and based on the reaction notation. From our viewpoint, stoichiometric equation is a vicarious (but not alternative!) concept when compared with mathematical equation applied for a given chemical/electrolytic system. From the GATES viewpoint, the stoichiometry is a superfluous concept provided that a sufficient physicochemical knowledge on partial reactions involved in a complex system is available.
Simulations on Metastable Systems
In a complex system, many particular reactions occur; the resultant reaction is the superposition of these reactions occurred with different efficiencies, known only after thorough physicochemical examination of the system. The physicochemical knowledge is based on (a) equilibrium constant values, referred to the equilibrium system, and (b) information about possible paths of particular reactions occurred in the system in question. Not all path of chemical reactions are accessible, under defined conditions of analysis, involved with temperature and/or presence of catalytic agents. For this purpose, the balances are completed by some intermediary species that may be formed, and completed by the related standard potentials and other equilibrium constants. Different “variations on the subject” that can be done for this purpose, are involved with “opening” the reaction paths. In all instances, the relationships between measurable quantities, i.e., E or pH and volume V of titrant added can be compared with the relationships obtained experimentally. Some examples of this kind are presented in [22,28].
The GEB, charge and concentration balances, together with the set of independent equilibrium constants, provide the numerical algorithm, implemented to software packages that support advanced programming, such as MATLAB computing environment [28]. The calculation procedure enables to get the desired relationships plotted in 2D or 3D space. It involves the plots of E=E(Φ), pH=pH(Φ), and speciation curves, 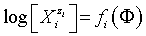
Graphical Presentation of the Data–an Example
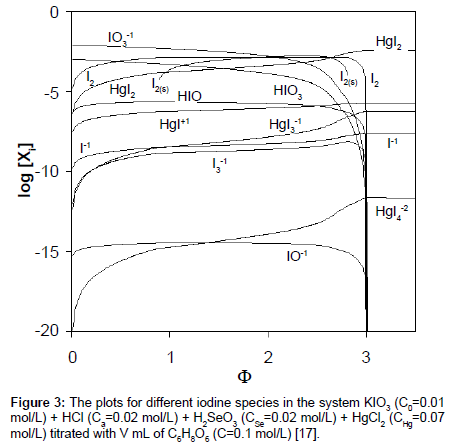
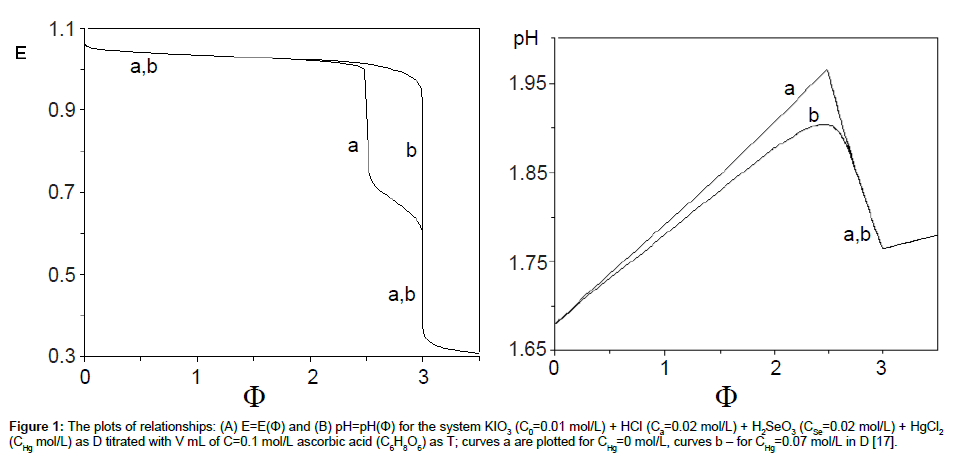
The plots of functions: E=E(Φ) and pH=pH(Φ), related to the system KIO3 (C0=0.01 mol/L) + HCl (Ca=0.02 mol/L) + H2SeO3 (CSe=0.02 mol/L) + HgCl2 (CHg mol/L) titrated with C6H8O6 (ascorbic acid) are presented in Figures 1A and 1B. The curves are plotted at CHg=0 mol/L, and the curves b at CHg=0.07 mol/L; the effect of HgCl2 as the side component in reaction between iodate and ascorbic acid is thus illustrated. Figure 1B indicates an example of non-monotonic plots of pH=pH(Φ) functions [17]. The speciation curves referred to iodine species, at CHg=0 mol/L and CHg=0.07 mol/L, are plotted in Figures 2 and 3. Among different curves presented in Figures 2 and 3, one can indicate the plots for solid iodine, I2(s), formed in intermediate part of the Φ-range; these parts of the related titration curves were discussed in [17,26,28]. It testifies on account of the opinion that the GATES/GEB provides far more valuable information than one gained from the wellknown Pourbaix diagrams.
Figure 1: The plots of relationships: (A) E=E(Φ) and (B) pH=pH(Φ) for the system KIO3 (C0=0.01 mol/L) + HCl (Ca=0.02 mol/L) + H2SeO3 (CSe=0.02 mol/L) + HgCl2(CHg mol/L) as D titrated with V mL of C=0.1 mol/L ascorbic acid (C6H8O6) as T; curves a are plotted for CHg=0 mol/L, curves b – for CHg=0.07 mol/L in D [17].
Generalizing Remarks
This review paper, relating principally to redox systems, shows that such systems can be described using real math (algebra), not “chemical mathematics”, consisting in juggling with chemical reaction equations. Redox reaction play fundamental role in biological systems [44-48], where GATES could also be applied-provided that the appropriate physicochemical knowledge, expressed by the equilibrium constants relating to elementary components of such systems is available. So far, such knowledge does not exist.
On the basis of partial, physicochemical information concerning the species in electrolytic redox systems, a thermodynamic knowledge of complex systems in constructed. Therein lies-from the GATES viewpoint-a synthesis of knowledge about these systems. The complexity of chemical systems is irrelevant in the context of computational power of modern computers. Just the qualitative (composition and charge of the species) and quantitative (equilibrium constants) knowledge is needed. Qualitative knowledge enables to involve concentrations of components and species in the respective (GEB, charge and concentration) balances, while the quantitative knowledge is determined by the interdependencies between concentrations of selected components, expressed by the equilibrium constants.
This knowledge applies to both static as well as dynamic systems. Information obtained from static redox systems, developed according to GATES/GEB principles, provides incomparably better quality of knowledge than obtained from the Pourbaix diagrams [49]. The plots obtained from GATES/GEB can be referred to any (not only predominant) species present in the system in question. Unlike the Pourbaix diagrams, potential E and pH of the system are calculated independently within GATES/GEB. Application of GATES/GEB to dynamic systems gives a new dimension, when compared with static systems.
An extremely important factor-especially when considering the biological systems-is an ensuring, that the knowledge of the oxidation degrees of the elements in simple or complex chemical species is unnecessary, from the point of view of the Approach II to GEB. In this respect, the necessary and sufficient knowledge is provided by chemical composition (expressed by chemical formula), and the external charge of particular species. In this context, it should be remembered that the oxidation degree of the elements is a contractual concept, perceived as the hypothetical charge that an atom would have if all bonds to atoms of different elements were ionic in 100% [50].
In the Approaches I and II to GEB, the species in electrolytic systems are considered in their natural forms, i.e., as hydrates in aqueous media, or mixed solvates in mixed-solvent media. Moreover, the roles of oxidants and reductants are not ascribed a priori to particular species in defined systems. This way, a kind of “democracy” is assumed in such systems
After calculations and graphical presentation of concentrations of particular species on the related speciation diagrams, we can formulate the chemical reactions proceeding in the system in question, together with relative efficiencies of these reactions
Final Comments
The principles of Science gaining are based on a conviction that complex phenomena occurred in Nature, e.g., in electrolytic systems, can be explained in terms of some general laws of the matter conservation; it is the basic assumption of reductionism. These laws are expressed in terms of mathematical equations, valid for the systems of any degree of complexity. Reductionism is very similar to and has its roots in Ockham’s razor principle that gives precedence to simplicity, i.e., the explanation which requires the fewest assumptions.
The power of reductionism lies in prediction and formulation; it is perceived as a good approximation of the macroscopic world. The knowledge thus obtained is verifiable and based on logical premises. This way, the quantitative knowledge gained from the study of relatively simple systems, can be synthesized in the knowledge obtainable from more complex systems. From this viewpoint, the knowledge obtained from physicochemical analysis involved e.g. with determination of the stability constants of complex species formed in a particular system can be perceived as a ‘stone’ used in construction of more complex systems. Any complex species must be equipped with its equilibrium constant value; only a qualitative knowledge (e.g., chemical formula) is insufficient in this respect. However, to construct the knowledge on more complex systems, these stones should be arranged according to a defined scheme (design), based on a set of compatible balances. Closely associated with reductionism is determinism the philosophy that everything has a cause, and that a particular cause leads to a unique effect; it means that under pre-assumed conditions nothing else could happen.
Before 1992, one basic segment needed for construction of the set of equations needed for resolution of redox systems was unknown; it was the electron balance, named later as GEB. The GEB, discovered in 1992, stems from the elements conservation law, and then are fully compatible with the equations known previously: the charge balance (expressing the law of charge conservation), and concentration balances, expressing the conservation of the individual elements forming the system. Solution of a set of k+2 nonlinear equations, complemented by relations between concentrations of some subsets of species, resulting from relations for the corresponding equilibrium constants, is not a problem when iterative computer programs are used for this purpose. Formally, the manner of resolution of this task is even easier than the one based on the formulation of some functional dependencies that require some simplifications, as a rule. The simplifications are not necessary in iterative methods. Moreover, incompetent/non-intended simplifications may lead to the set of contradictory equations, impossible to resolution from mathematical viewpoint, see [32]. The simplifications made towards obtaining specific, functional dependencies between some variables have nothing common with the Occam’s razor principle and distort the reality, as a rule. Any sophisticated computer program using an “ersatz” (relative to GEB) for resolution of electrolytic systems cannot give the results desired.
The combination 2·f(O)–f(H) of elemental balances for H and O (Approach II to GEB) is the quintessence of the electron balance that was the missing link needed for description of electrolytic redox systems, of any degree of complexity. The Approach II to GEB can be perceived as the real expression of Harmonia Mundi, and as the powerful testimony of the World Harmony, Harmony of Nature. GATES, and GATES/GEB in particular, are clear confirmation of the fact that the Nature is designed mathematically and the true laws of nature are mathematical, in principle. In other words, the quantitative mathematical method became the essence of Science.
Instead of Epilogue
Thomas Kuhn-the renowned philosopher of science, wrote in this book “The Structure of Scientific Revolutions”, published in 1962, about an epistemological paradigm, involved with revolutionary shifts in science [51]. According to Kuhn, a good paradigm should (1) be consistent, both logically and conceptually; (2) be possibly simple and contain only those concepts and theories, which are really necessary for the science; (3) provide the ability to create a detailed theory, consistent with the known facts
GATES/GEB is an example of good/excellent paradigm.
The Kuhn’s fundamental argument was that a conventional route for the mature science is the revolutionary transition from one paradigm to another. When a paradigm is changed, the scientific world is changing qualitatively and quantitatively, and the science is enriched by quite new facts and theories. Kuhn also argued that-contrary to common opinion-typical scientists are not objective and independent thinkers, but conservatives, who agree with what they have been taught and apply this science (knowledge) to solve problems according to the dictates of theory learned by them
The man who tries to solve the problem within the existing knowledge and technique, directs his thoughts in accordance with his learned knowledge. Consequently, researchers tend to ignore and fight against the development of a new, competitive paradigm that may threaten the existing paradigm
References
- Michalowski T, Rokosz A, Tomsia A (1987) Determination of basic impurities in mixture of hydrolysable salts. Analyst 112: 1739-1741.
- Michalowski T (1988) Possibilities of application of some new algorithms for standardization purposes; Standardization of sodium hydroxide solution against commercial potassium hydrogen phthalate. Analyst 113: 833-935.
- Michalowski T, Rokosz A, Negrusz-Szczesna E (1988) Use of Pad approximants in the processing of pH titration data; Determination of the parameters involved in the titration of acetic acid. Analyst 113: 969-972.
- Michalowski T, Rokosz A, Koscielniak P, Lagan JM, Mrozek J (1989) Calculation of concentrations of hydrochloric and citric acids together in mixture with hydrolysable salts. Analyst 114: 1689-1692.
- Michaowski T (1992) Some new algorithms applicable to potentiometric titration in acid-base systems. Talanta 39: 1127-1137.
- Michaowski T, Gibas E (1994) Applicability of new algorithms for determination of acids, bases, salts and their mixtures. Talanta 41: 1311-1317.
- Janecki D, Doktr K, Michaowski T (1999) Determination of stability constants of complexes of MiKjHkL type in concentrated solutions of mixed salts. Talanta 48: 1191-1197.
- Janecki D, Styszko-Grochowiak K, Michaowski T (2000) The catenation and isomerisation effects on stability constants of complexes formed by some diprotic acids. Talanta 52: 555-562.
- Michaowski T, Pilarski B, Asuero AG, Dobkowska A (2010) A new sensitive method of dissociation constants determination based on the isohydric solutions principle. Talanta 82: 1965-1973.
- Michaowski T, Pilarski B, Asuero AG, Dobkowska A, Wybraniec S (2011) Determination of dissociation parameters of weak acids in different media according to the isohydric method. Talanta 86: 447-451.
- Michalowski T, Asuero AG (2012) Formulation of the system of isohydric solutions. JASMI 2: 1-4.
- Asuero AG, Pilarski B, Dobkowska A, Michaowski T (2013) On the isohydricity concept--some comments. Talanta 112: 49-54.
- Pilarski B, Dobkowska A, Foks H, Michaowski T (2010) Modelling of acid-base equilibria in binary-solvent systems: A comparative study. Talanta 80: 1073-1080.
- Michalowski T, Lesiak A (1994) Acid-base titration curves in Disproportionating Redox Systems. J Chem Educ 71: 632-636.
- Michalowski T (2002) Effect of mutual solubility of solvents in multiple extraction. J Chem Educ 79: 1267-1268
- Michalowski T (1994) Calculation of pH and potential E for bromine aqueous solutions. J Chem Educ 71: 560-562
- Michalowski T, Lesiak A (1994) Formulation of generalized equations for redox titration curves. Chemia Analityczna 39: 623-637.
- Michalowski T, Wajda N, Janecki D (1996) A unified quantitative approach to electrolytic systems. Chemia Analityczna 41: 667-685.
- Michalowski T (2001) Calculations in Analytical Chemistry with Elements of Computer Programming. PK, Cracow.
- Michalowski T, Baterowicz A, Madej A, Kochana J (2001) An extended Gran method and its applicability for simultaneous determination of Fe(II) and Fe(III). Anal Chim Acta 442: 287-293.
- Michaowski T, Toporek M, Rymanowski M (2005) Overview on the Gran and other linearisation methods applied in titrimetric analyses. Talanta 65: 1241-1253.
- Michalowski T, Rymanowski M, Pietrzyk A (2005) Non-typical Brnsteds acids and bases. J Chem Educ 82: 470-472.
- Michaowski T, Kupiec K, Rymanowski M (2008) Numerical analysis of the Gran methods. A comparative study. Anal Chim Acta 606: 172-183.
- Ponikvar M, Michaowski T, Kupiec K, Wybraniec S, Rymanowski M (2008) Experimental verification of the modified Gran methods applicable to redox systems. Anal Chim Acta 628: 181-189.
- Michalowski T (2007) Complementarity of physical and chemical laws of preservation in aspect of electrolytic systems (in Polish). Wiadomosci Chemiczne 61: 625-640.
- Michalowski T (2010) The generalized approach to electrolytic systems: I. Physicochemical and analytical implications. Crit Rev Anal Chem 40: 2-16.
- Michalowski T, Pietrzyk A, Ponikvar-Svet M, Rymanowski M (2010) The generalized approach to electrolytic systems: II. The generalized equivalent mass (GEM) concept. Crit Rev Anal Chem 40: 17-29.
- Michalowski T (2011) Application of GATES and MATLAB for Resolution of Equilibrium, Metastable and Non-Equilibrium Electrolytic Systems. In: Michalowski T, Applications of MATLAB in Science and Engineering, Chapter 1, InTech - Open Access publisher in the fields of Science, Technology and Medicine 1-34.
- Michalowski T, Ponikvar-Svet M, Asuero AG, Kupiec K (2012) Thermodynamic and kinetic effects involved with pH titration of As(III) with iodine in a buffered malonate system. J Solution Chem 41: 436-446.
- Michalowski T, Toporek M, Michalowska-Kaczmarczyk AM, Asuero AG (2013) New trends in studies on electrolytic redox systems. Electrochimica Acta 109: 519–531
- Michalowski T, Michalowska-Kaczmarczyk AM, Toporek M (2013) Formulation of general criterion distinguishing between non-redox and redox systems. Electrochimica Acta 112: 199-211
- Michalowska-Kaczmarczyk AM, Michalowski T (2013) Comparative balancing of non-redox and redox electrolytic systems and its consequences. American Journal of Analytical Chemistry 4: 46-53
- Michalowski T, Pilarski B, Asuero AG, Michalowska-Kaczmarczyk AM (2014) Modeling of acid-base properties in binary-solvent systems. In: George W, Handbook of Solvents, ChemTec Publishing, Toronto.
- Michalowska-Kaczmarczyk AM, Michalowski T (2014) Compact formulation of redox systems according to GATES/GEB principles. JASMI 4: 39-45
- Michalowska-Kaczmarczyk AM, Asuero AG, Toporek M, Michalowski T (2014) Why not stoichiometry versus Stoichiometry why not?o Part I. General context, Critical Reviews in Analytical Chemistry. BATC-2014-0025.
- Michalowska-Kaczmarczyk AM, Asuero AG, Toporek M, Michalowski T (2014) Why not stoichiometry versus Stoichiometry why not? Part II. GATES in context with redox systems, Critical Reviews in Analytical Chemistry. BATC-2014-0026.
- Michalowska-Kaczmarczyk AM, Michalowski T, Toporek M, Asuero AG (2014) Why not stoichiometry versus Stoichiometry why not? Part III, Extension of GATES/GEB on Complex Dynamic Redox Systems, Critical Reviews in Analytical Chemistry - Manuscript IDBATC-2014-0032.
- Michalowski T, Pilarski B, Dobkowska A, Mlodzianowski J (2010) Mathematical modeling and physicochemical studies on acid-base equilibria in binary-solvent systems. Wiadomosci Chemiczne 54: 124-154.
- Michaowski T, Pietrzyk A (2006) A thermodynamic study of struvite+water system. Talanta 68: 594-601.
- Michalowski T, Toporek M, Rymanowski M (2007) pH-Static Titration: A quasistatic approach. J Chem Educ 84: 142-150.
- Michalowski T, Asuero AG, Ponikvar-Svet M, Toporek M, Pietrzyk A, et al. (2012) Principles of computer programming applied to simulated pHstatic titration of cyanide according to a modified Liebig-Denigs method. Journal of Solution Chemistry 41: 12241239.
- Asuero AG, Michalowski T (2011) Comprehensive formulation of titration curves referred to complex acid-base systems and its analytical implications. Crit Rev Anal Chem 41: 151-187.
- Michalowski T, Asuero AG (2012) New approaches in modeling the carbonate alkalinity and total alkalinity. Crit Rev Anal Chem 42: 220-244
- Pietrzkowski Z, Nemzer B, Sprna A, Stalica P, Thresher W, et al. (2010) Influence of betalain-rich extract on reduction of discomfort associated with osteoarthritis. New Medicine 1: 1217
- Nemzer B, Pietrzkowski Z, Sprna A, Stalica P, Thresher W, et al. (2011) Betalainic and nutritional profiles of pigment-enriched red beet root (Beta vulgaris L.) dried extracts. Food Chem 127: 4253
- Wybraniec S, Michaowski T (2011) New pathways of betanidin and betanin enzymatic oxidation. J Agric Food Chem 59: 9612-9622.
- Wybraniec S, Stalica P, Sprna A, Nemzer B, Pietrzkowski Z, et al. (2011) Antioxidant activity of betanidin: electrochemical study in aqueous media. J Agric Food Chem 59: 12163-12170.
- Wybraniec S, Starzak K, Skopinska A, Szaleniec M, Slupski J, Mitka K, Kowalski P, Michalowski T (2013) Effects of metal cations on betanin stability in aqueous-organic solutions. Food Sci Biotechnol 22: 353-363.
- Pourbaix M (1974) Atlas of electrochemical equilibria in aqueous solutions. 2nd Edition, National Association of Corrosion Engineers, Houston, Tex.
- Wikipedia (2014) Oxidation state.
- Wikipedia (2014) Paradigm shift.
Relevant Topics
Recommended Journals
Article Tools
Article Usage
- Total views: 15195
- [From(publication date):
September-2014 - Aug 20, 2025] - Breakdown by view type
- HTML page views : 10547
- PDF downloads : 4648

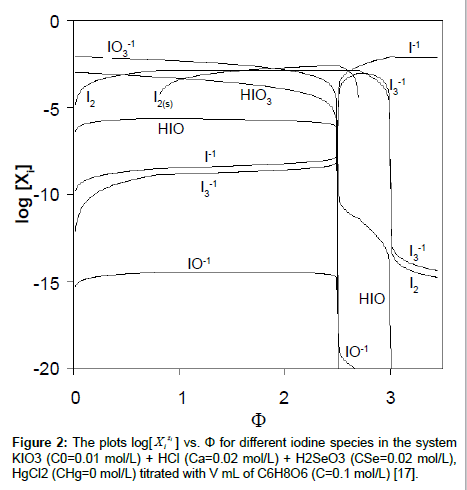
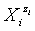 vs. Φ for different iodine species in the system KIO3 (C0=0.01 mol/L) + HCl (Ca=0.02 mol/L) + H2SeO3 (CSe=0.02 mol/L), HgCl2 (CHg=0 mol/L) titrated with V mL of C6H8O6 (C=0.1 mol/L) [17].
vs. Φ for different iodine species in the system KIO3 (C0=0.01 mol/L) + HCl (Ca=0.02 mol/L) + H2SeO3 (CSe=0.02 mol/L), HgCl2 (CHg=0 mol/L) titrated with V mL of C6H8O6 (C=0.1 mol/L) [17].