Polymeric Membranes: Effects of Catalyst Volume Fraction on Dielectric Relaxation Time and Crystallites Dimensions

Laurentiu Iordaconiu¹, Iosif Malaescu¹, Liviu Chirigiu² and Ioan Bica^1*

¹West University of Timisoara, Timisoara, Romania

²University of Medicine and Pharmacy of Craiova, Craiova, Romania

*Corresponding Author:

Ioan Bica
West University of Timisoara
Bd. V. Parvan, nr.4
300223-Timisoara, Romania
Tel: +40-(0)256-592111
E-mail: ioanbica50@ yahoo.com

Received date: February 16, 2016; Accepted date: February 24, 2016; Published date: February 29, 2016

Citation: Iordaconiu L, Malaescu I, Chirigiu L, Bica I (2016) Polymeric Membranes: Effects of Catalyst Volume Fraction on Dielectric Relaxation Time and Crystallites Dimensions. Ind Chem 2:117. doi:10.4172/2469-9764.1000117

Copyright: © 2016 Iordaconiu L, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Visit for more related articles at Industrial Chemistry

Abstract

We have obtained polymeric membranes based on silicone rubber, stearic acid, silicone oil at various concentrations of catalyst. The obtained polymeric membranes are used as dielectric materials for fabricating plane capacitors. By using the plane capacitor method, we measure capacitance C and dissipation factor D of the plane capacitors in an electric field of medium frequency. From the obtained data we calculate the dispersion and absorption characteristics of the membranes. We show that these characteristics are sensibly influenced by dimensions of the crystallites which in turn, depend on the concentration of catalyst used at polymerization of silicone rubber.

Keywords

Polymeric membranes; Silicone rubber; Relaxation time; Dielectric polarization; Plane capacitor

Introduction

Membranes are materials used frequently in fabrication of devices for liquid phase transfer [1-7] with small energy consumption from one side to another. Inspired mainly from biology, membranes are fabricated from metals and ceramics [1-4], and in last years an important source of fabrication has become composite polymeric membranes [5-7]. The selective transfer of phases through membranes is realized by various methods: pressure and concentration gradient, electric field etc. Based on these methods, the main applications are in water desalination and filtering, blood detoxification etc.

Recently, porous membranes have been fabricated by polymerization of Silicone Rubber (SR) at various concentrations of catalyst (CA) [8,9]. It was shown that dielectric properties, as well as pore’s diameters, density and distribution are sensibly influenced by the volume concentration of the catalyst.

In this paper, we underline the mechanisms leading to dielectric properties of interest for various technical and medical applications of polymeric membranes based on SR, stearic acid (SA), silicone oil (SO) and various concentrations of C.

Membrane Preparation and Capacitors

The materials used for fabricating the membranes is SR (RTV 3325 type) with CA, from Bluestar-Silicone [10] and SO and SA from Merck [11]. For well-chosen quantities of SR, SO and SA, a viscous and liquid mixture is prepared following the method described in Reference [8,9]. From this mixture we take four samples of equal volumes. Then, each mixture is again mixed and homogenized with a different quantity of CA. Finally four samples of liquid solutions are obtained, as following:

• Sample S₁ with 5% vol. of CA;

• Sample S₂ with 10% vol. of CA;

• Sample S₃ with 15% vol. of CA, and

• Sample S₄ with 20% vol. of CA.

Each of the obtained solutions is introduced between the Cu plates of the capacitor with dimensions 0.11 × 0.10 × 0.00042 m³. In about 24 h, SR becomes polymerized and we obtain:

• Capacitor K₁ with 5% vol. of CA;

• Capacitor K₂ with 10% vol. of CA;

• Capacitor K₃ with 15% vol. of CA, and

• Capacitor K₄ with 20% vol. of CA.

Experimental Results and Discussions

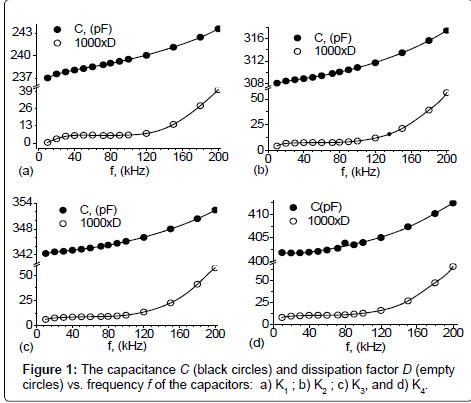
Capacitors K_i (i=1, 2, 3, 4) are connected, in turn, to the RLC – meter type NM 8118. One measures the capacitance C and the dissipation factor D in an electric field with frequencies between 10 kHz and 200 kHz. The obtained values are plotted in Figure 1. A general feature is that the data C=C (f) can be approximated by a second degree polynomial. A second important feature is that the capacitance increases with increasing the electric field frequency and is sensibly influenced by the volume fraction of the catalyst. Variation of the dissipation factor of the capacitors K_i (i=1, 2, 3, 4) is characterized by three distinct regions (Figure 1). The length of each region depends on the volume fraction of the catalyst and by the frequency of the electric field.

The relative dielectric permittivity of the dielectric between the plates of the capacitors is calculated according to:

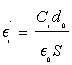(1)

with i=1, 2, 3, 4, C_i is the capacitance of the capacitor K_i, d_o is the thickness of the membrane, E₀ is vacuum dielectric permittivity, and S is the common surface of the capacitor’s plates. Using numerical values d₀=0.00042 m, E₀=8.85×10^(-12) F/m and S=11×10^-3 m² into Equation (1), we obtain:

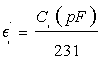(1’)

Using the dependence C_i=C_i(ω=2πf) from Figure 1, into Equation (1’) we obtain the permittivity E_i=E_i (ω), as shown in Figure 2. The main feature is that the relative dielectric permittivity of the membranes increases with the frequency and is sensibly influenced by the volume fraction of the catalyst.

Figure 1: The capacitance C (black circles) and dissipation factor D (empty circles) vs. frequency f of the capacitors: a) K₁ ; b) K₂ ; c) K₃, and d) K₄.

Using the theory of dielectrics we can write the dielectric loss factor such as [1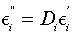2]

(2)

Introducing into Equation (2) the dependence C_i=C_i(ω=2πf) from Figure 1, and respectively the dependence E_i ’ = E_i ’ (ω), from Figure 2, we obtain the variation of the dielectric loss factor E_i ’’ =E_i ’’ (ω), as shown in Figure 3. The results show that the dielectric loss factor of the membranes is characterized, as in the case of the dissipation factor D, by three distinct ranges whose length depends on ω and on the volume fraction ɸ.

Figure 2: Variation of relative dielectric permittivity E' with the frequency ω=2πf, at various values of catalyst volume fraction for the capacitors: a) K₁ ; b) K₂ ; c) K₃, and d) K₄.

Figure 3: Variation of the dielectric loss factor E" of the composite membranes as a function of the frequency ω=2πf and of volume fractionɸ of the catalyst, for the capacitors: a) K₁ ; b) K₂ ; c) K₃, and d) K₄.

In the framework of the Debye theory for dielectrics with a single relaxation time, the quantities E_i’ and E_i ’’ are the real part (dispersion characteristic), and respectively the imaginary part (absorption characteristic) of the complex relative dielectric permittivity [12,1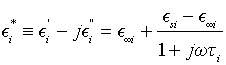3].

(3)

where E_∞i is the relative dielectric permittivity for ω→∞, E_si is the relative dielectric permittivity for ω=0, 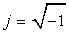, T_i is the relaxation time of dielectric polarization, and i=1, 2, 3, 4. From the second part of Equation 3, we obtain the equalities

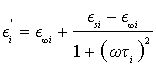(4)

and, respectively

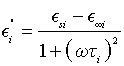(5)

By eliminating the quantity 1+ (ωT_i)² between Equations (4) and (5) we obtain

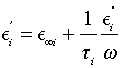(6)

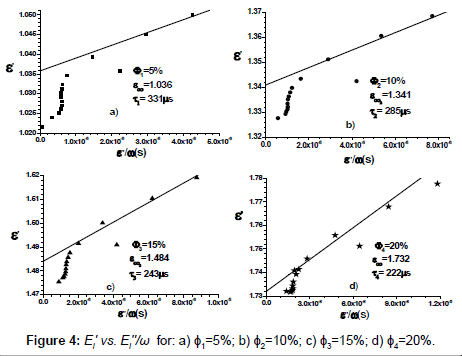
which is the equation of a straight line in the coordinate system (O, E_i ”/ω, E’) with the slope 1/ T_i and intersecting E’-axis at the point (0, E’_∞). Using data from Figures 2 and 3, we obtain 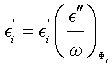, and together with Equation (6) we obtain the linear dependence illustrated in Figure 4. The result shows that E_∞i increases with increasing ɸ_i, while T_i decreases with increasing ɸ_i

Figure 4: E_i' vs. E_i''/ω for: a) ɸ₁=5%; b) ɸ₂=10%; c) ɸ₃=15%; d) ɸ₄=20%.

In the presence of the catalyst, crystallites are formed inside the silicone rubber viscoelastic matrix. We consider that crystallites are monodisperse and their radius is r.

Then, under the influence of electric field, the crystallites begin to rotate inside the matrix. In a first approximation, we consider also that the viscosity �? of the elastic matrix is not influenced by the volume fractions ɸ_i of the catalyst. Thus, the energy used for the friction is given by

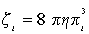(7)

Then, the relaxation time T_i in the absence of Mosotti field is given by [12]

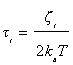(8)

Where k_B is Boltzmann’s constant and T is the temperature. Finally, introducing Equation (7) into Equation (8), we can write the radius of the crystallites, such as:

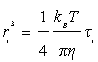(9)

Using the values of relaxation times from Figure 4, we obtain the following values for the radii:

Equation 10 shows that an increase of 5% (from 5% to 10%) in the volume fraction of the crystallites leads to a decrease with 8% of their radii. In a similar manner, an increase of 10% (from 5% to 15%) of the volume fraction leads to a decrease with 11% of the radii, while an increase of 15% leads to a decrease with 13% of crystallites radii.

An important factor which can explain qualitatively the obtained radii of crystallites formed inside this type of membranes is their geometrical microstructure. In this sense, small-angle neutron scattering (SANS) investigations have shown [13] that at concentrations higher than 5% the membranes are characterized by a hierarchical organization of crystallites in which ramified mesoscale mass fractals [14] crystallites with fractal dimension D=2.68 are composed of either mass or surfacelike, nano fractal crystallites of various fractal dimensions, whose values depend on the catalyst concentration. In the same work it has been shown that the transition from mass to surface fractal occurs between 10% and 20% volume concentration of the catalyst and at this point the small crystallites change their organization, from branched structures to compact structures with rough surfaces. In general, for hierarchically organized membranes [15,16], SANS can reveal a transition from one type of organization to another one (e.g., massto- mass, mass-to-surface or any combination of them), and depending on the type of the transition, various characteristics can be revealed. If the SANS scattering intensity shows a succession of two power-law regimes in which the absolute value of the first power-law regime is higher than that of the subsequent second power-law regime, and the crossover position (point in reciprocal space where the transition occurs) depends on the contrast variation, then we deal with a multiphase material [16]. Thus, applying a generalized Stuhrmann contrast variation [17] we can answer whether one phase ‘absorbs’ another one, or they are both immersed in the surrounding matrix. However, if the absolute value of the first power-law regime is lower than that of the subsequent second power-law regime, this is a signature of a two-phase fat fractal [18-20] and additional information can be obtained from corresponding SANS data, such as the scaling factor at each iteration or the number of particles composing the fractal [21,22].

Other physical or chemical properties of the obtained membranes, such as the absorption and dispersion characteristics, pore distribution and their average diameter [8], as well as gelation time [9] can be sensibly influenced by the volume concentration of the catalyst.

Conclusions

We have shown that the electrical capacitance C and dissipation factor D of the obtained capacitors based on silicone rubber, silicone oil, stearic acid and catalyst; change their values in the presence of an electric field of medium frequency, and the corresponding profile is sensibly influenced by the volume fraction ɸ of the catalyst. In addition, the relative dielectric permittivity E’ and dielectric loss factor E’’ depend also on the volume concentration ɸ, for electric field frequencies in the range from 10 to 100 KHz.

Dielectric measurements show that the relaxation time of dielectric polarization for each membrane decreases with increasing the concentration ɸ, while the crystallite size decreases with increasing ɸ. We have developed a mathematical model in the framework of Debye theory which explains this behavior. The obtained results are in good agreement with the behavior of the radius of gyration of nanocrystalites, as revealed by small-angle neutron scattering measurements [13].

These properties can be used for various medical and technical applications, such as in phase separation using electrical methods, or for fabrication of devices in which dispersion and absorption of an electric field have to be predetermined.

Acknowledgments

Financial support from JINR-IFIN-HH projects awarded by the Romanian Plenipotentiary Representative at JINR is acknowledged.

References

1. Ulbricht M (2006) Advanced functional polymer membranes. Polymer 47: 2217-2262.
2. Schultz A, Steinbach F, Caro J (2014) Pressed graphite crystals as gas separation membrane for steam reforming of ethanol. J Membr Sci 469: 284-291.
3. Chen Y, Qian B, Hao Y, Liu SH, Tade MO, et al. (2014) Influence of sealing materials on the oxygen permeation fluxes of some typical oxygen ion conducting ceramic membranes. J Membr Sci 470: 102-111.
4. Ravkina O, Klande T, Feldhoff A (2015) Investigation of carbonates in oxygen-transporting membrane ceramics. J Membr Sci 480: 31-38.
5. Ahmad AL, Adewole JK, Leo CP, Ismail S, Sultan AS, et al. (2015) Prediction of plasticization pressure of polymeric membranes for CO2 removal from natural gas. J Membr Sci 480: 39-46.
6. Kubackza A (2014) Prediction of Maxwell–Stefan diffusion coefficients in polymer–multicomponent fluid systems. J Membr Sci 470: 389-398.
7. Mulder M (2006) Basic Principles of Membranes Technology. 2nd edn. Dordrecht: Kluwer Academic Publishers.
8. Cirtina G, Balasoiu M, Anitas EM, Bortun CM, Ionescu C, et al. (2015) Silicone rubber membranes: Influence of the electric field of medium frequency on the dielectric properties. Journal of Optoelectronics and Advanced Materials 17: 1891-1895.
9. Bica I, Anitas EM, Bunoiu M, Iordaconiu L, Bortun CM, et al. (2016) Microparticles and Electroconductive Magnetorheological suspensions. Rom Journ Phys,p: 61.
10. www.bluestarsilicones.com
11. www.merckmillipore.com
12. Ahmad Z (2012) Polymeric Dielectric Materials. INTECH Open Science.
13. Anitas EM, Bica I, Erhan RV., Bunoiu M, Kuklin AI (2015) Structural Properties of Composite Elastomeric Membranes Using Small-Angle Neutron Scattering. Rom Journ Phys 60: 653-657.
14. Anitas EM (2015) Microscale Fragmentation and Small-Angle Scattering from Mass Fractals. Adv Cond Matt Phys. Article ID 501281.
15. Garab G (2014) Hierarchical organization and structural flexibility of thylakoid membranes. Biochim Biophys Acta 1837: 481-494.
16. Mendil-Jakani H, Pouget S, Gebel G, Pintauro PN (2015) Insight into the multiscale structure of pre-stretched recast Nafion® membranes: Focus on the crystallinity features. Polymer 63: 99-107.
17. Bica I, Anitas EM, Averis LME, Bunoiu M (2015) Magnetodielectric effects in composite materials based on paraffin, carbonyl iron and grapheme. J Ind Eng Chem 21: 1323-1327.
18. Cherny Y, Anitas EM, Osipov VA, Kuklin AI (2014) Small-angle scattering from multiphase fractals. J Appl Cryst 47:198-206.
19. Grebogi C, McDonald SW, Ott E, Yorke JA (1985) Exterior Dimensions Exterior of Fat Fractal. Phys Lett A 110: 1-4.
20. Farmer JD (1985) Sensitive dependence on parameters in nonlinear dynamics. Phys Rev Lett 55: 351-354.
21. Umberger DK, Farmer JD (1985) Fat fractals on the energy surface. Phys Rev Lett 55: 661-664.
22. Anitas EM (2014) Small-angle scattering from fat fractals. Eur Phys J B 87: 13-143.