Stereoscopic Memory When Stimuli No Longer Persist: Void and Binocular Intervals in Alternating Monocular Presentations

It was early realized by Exner in 1875 that stereopsis could occur when both eyes together receive the two images of a stereo pair one after the other [1]. Stereopsis occurs even when a void interval is inserted between the presentations of each image. For instance, Ogle [2] found that stereopsis occurred when two 18 ms presentations were separated by a void interval of 100 ms. Stereopsis has also been studied with protocols in which the two images of a stereo pair were presented cyclically, in alternation to the two eyes (Figure 1a). Guilloz [3] - who was motivated by a practical interest in 3d X-ray radioscopy - produced cyclical presentations to the two eyes using a disk rotating in front of a stereoscope's lenses. He also described how natural scenes are perceived through his apparatus. He found that trained observers could form stable 3d interpretations even at one cycle per second (an alternation of 500 ms monocular presentations), implying that perfect sensation of stereoscopic depth may rely on judgements continually piling up (“jugements surajoutés continument”) though the judgements are formed with the help of successive impressions which are nearly or fully erased while the next takes place [4].

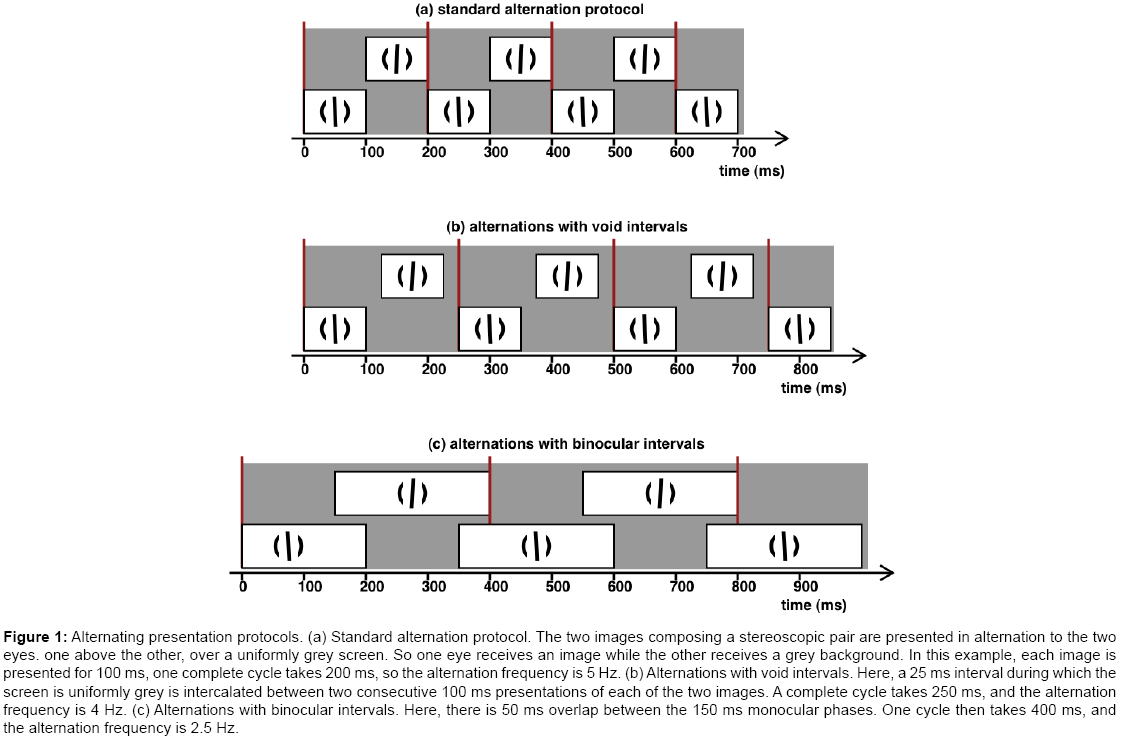
Figure 1: Alternating presentation protocols. (a) Standard alternation protocol. The two images composing a stereoscopic pair are presented in alternation to the two eyes. one above the other, over a uniformly grey screen. So one eye receives an image while the other receives a grey background. In this example, each image is presented for 100 ms, one complete cycle takes 200 ms, so the alternation frequency is 5 Hz. (b) Alternations with void intervals. Here, a 25 ms interval during which the screen is uniformly grey is intercalated between two consecutive 100 ms presentations of each of the two images. A complete cycle takes 250 ms, and the alternation frequency is 4 Hz. (c) Alternations with binocular intervals. Here, there is 50 ms overlap between the 150 ms monocular phases. One cycle then takes 400 ms, and the alternation frequency is 2.5 Hz.

In later studies (references in [5]) the occurrence of stereopsis was studied as a function of three main parameters: presentation rates (measured in cycles per second), delays between presentations, and stimuli intensity — weaker luminance goes with weaker stimuli and stronger persistence. In a review on stereopsis, Ogle [6] mentions that after-images persisting as long as twenty minutes led to the perception of stereoscopic depth for as long as four minutes.

The current explanation for stereopsis from temporally separated images is that (i) each stimulus leaves a trace during its presentation time plus a persistence time and that (ii) if the presentation plus persistence times of the two images presented in alternation overlap, stereoscopic calculations may be performed during this overlap period [2,5,7]. All authors agree with the fact that stereopsis needs several cycles to develop whenever an alternation protocol is used.

In an early model, Engel [5] considered that stereoscopic depth could last beyond the overlap period - so he assumed the existence of a kind of stereoscopic memory. However his experiments and the very similar earlier experiments of Efron [8] did not allow one to assign independent durations to the overlap time and the purely stereoscopic memory duration. Furthermore, in Engel's model, the stereoscopic calculations are assumed to be nearly instantaneous, thus the model did not explain why more than one presentation cycle was needed.

On the other hand, our main motivation for studying stereopsis under alternating presentation conditions was to collect data on the processing time needed for various classes of stimuli, thus throwing some light on the various problems encountered in the construction of a 3d interpretation. In our previous work on stereopsis under alternating presentation conditions [9] we did not use void intervals, but systematically varied monocular presentation times. As stereoscopic stimuli grew in complexity, smaller and smaller alternating monocular presentation times, - creating higher and higher alternation frequencies - were required to obtain stereopsis. Starting from an average 2.5 Hz frequency for the easiest stereograms, containing two to four simple disjoint elements (circles, arcs, rectangles), higher frequency values “were needed for stimuli containing slanted elements or curved surfaces (about 1 Hz increment), overlapping elements at two different depths (about 2.5 Hz increment), or camouflaged overlapping surfaces (>7 Hz increment)” [9]. We proposed that “during the construction of the threedimensional percept, the loss of information due to natural decay of stimuli traces must be compensated by refreshes of visual input”. Therefore, we proposed that beyond the phenomenon of static stereoscopic persistence that extends beyond the persistence of monocular inputs, there was also an active process of refinement of a stereoscopic memory store, fed by monocular inputs.

In order to obtain more detailed information on the temporal aspects of stereoscopic interpretation with various stimuli, we extended our previous work by intercalating either (i) variable void intervals between the monocular presentation times (Figure 1b) or (ii) variable binocular intervals (Figure 1c). For each selected value of the void, or the binocular interval, we increased the duration of the monocular intervals, and determined whether the subject experienced stable stereopsis, pulsating (discontinuous) stereopsis, or no stereopsis at all. The use of intercalated binocular intervals produced important, unexpected results.

First, a modest increase in the duration of the binocular interval makes possible a much larger increase in the duration of the purely monocular presentations. This suggests that the information that is acquired during truly binocular presentations might be more reliable and less subject to decay than the information acquired during the persistence overlap periods.

Second, as the binocular duration increases, we find three different phases, a phase in which there is a transition between stereopsis and no stereopsis, a later phase in which there is a transition from stable stereopsis to pulsating stereopsis, then from pulsating stereopsis to no stereopsis and an intermediate paradoxical phase in which, we propose, the pulsating character of stereopsis does not reach consciousness, and the subject reports stable stereopsis.

Third, a pair of closely related stimuli that could be hardly differentiated in our previous work under strict monocular alternations [9] can now give rise, in some subjects, to strikingly different behaviours at large binocular intervals. The use of these intervals thus increases considerably the alternation presentation technique as a tool to reveal subtle processing differences between closely related stimuli.

Subjects

Five subjects (12-18 years, 3 males, 2 females) belonging to a boarding school and author S.R. (39 years), part time physician associated to the school, took part in systematic experiments. Two subjects and author S.R. had normal vision (1.0/1.0 acuities) in both eyes without correction, and three subjects had modest myopia or hypermetropia that were corrected to normal with refractive lenses. All subjects had normal responses to standard clinical tests for binocular vision (Worth, Lang, and Fly tests). All subjects or their parents gave their written consent for their participation in the tests.

Stimuli

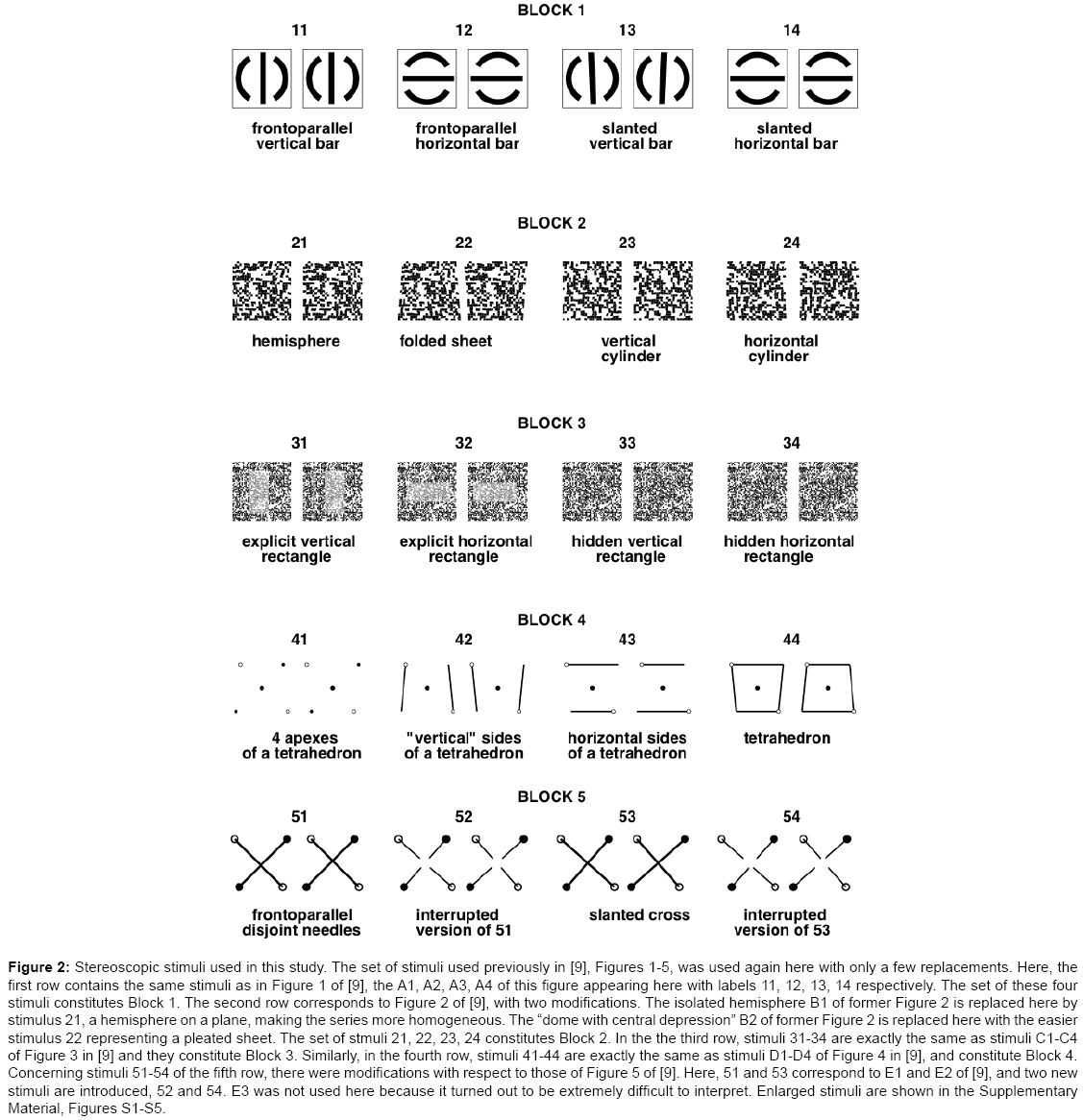
As in previous work [9], we used a set of twenty different stereoscopic stimuli designed to probe various aspects of stereoscopic processing (slant, curvature, occlusion, camouflage). The stimuli were grouped in five blocks, each containing a series of four stereoscopic pairs (Figure 2, enlarged versions are shown in the Supplementary Material, Figures S1-S5). We used the same twenty stimuli as in our previous work, except three (one from the second series, two from the fifth). Two of them were replaced with simpler ones; the third was necessitated by the replacement of the second. The stimuli were generated on-the-fly. The images were 4.5 cm wide, and they were viewed at 40 cm, thus each image subtended approximately 6.4 degrees on the screen.

Figure 2: Stereoscopic stimuli used in this study. The set of stimuli used previously in [9], Figures 1-5, was used again here with only a few replacements. Here, the first row contains the same stimuli as in Figure 1 of [9], the A1, A2, A3, A4 of this figure appearing here with labels 11, 12, 13, 14 respectively. The set of these four stimuli constitutes Block 1. The second row corresponds to Figure 2 of [9], with two modifications. The isolated hemisphere B1 of former Figure 2 is replaced here by stimulus 21, a hemisphere on a plane, making the series more homogeneous. The “dome with central depression” B2 of former Figure 2 is replaced here with the easier stimulus 22 representing a pleated sheet. The set of stmuli 21, 22, 23, 24 constitutes Block 2. In the the third row, stimuli 31-34 are exactly the same as stimuli C1-C4 of Figure 3 in [9] and they constitute Block 3. Similarly, in the fourth row, stimuli 41-44 are exactly the same as stimuli D1-D4 of Figure 4 in [9], and constitute Block 4. Concerning stimuli 51-54 of the fifth row, there were modifications with respect to those of Figure 5 of [9]. Here, 51 and 53 correspond to E1 and E2 of [9], and two new stimuli are introduced, 52 and 54. E3 was not used here because it turned out to be extremely difficult to interpret. Enlarged stimuli are shown in the Supplementary Material, Figures S1-S5.

Stimulus presentation

An interactive computer graphics program was written in the C++ language and OpenGL to produce the stereograms on a computer screen. This program will be sent upon request to author J N. The images were presented in alternation, either (i) in immediate alternation to the two eyes, one eye receiving the stimulus and the other eye receiving the screen's grey background (Figure 1a) or (ii) with a void interval between the presentations of the left and right images, the eyes receiving the grey background of the screen during the void interval (Figure 1b), or (iii) with a binocular presentation interval intercalated between the left and right presentations (Figure 1c). Viewing conditions were photopic. The experiments were run in Moscow using a Samsung laptop computer with a 1024 × 600 pixels LCD screen. Presentation times were first measured in frame counts. The frame numbers were shown on the screen. For each kind of stimulus, we measured the number of frames per minute and used this observed frame turnover to re-express the durations in milliseconds. The observed durations agreed with a 80/s refresh rate under most conditions, except in the case of the experiments in Block 2 (80/s for void intervals, 60/s for monocular or binocular intervals) and those in Block 3 (80/s for void intervals, 40/s for monocular intervals, 30/s for binocular intervals).

Procedures

The two images of a stereogram were presented, according to the Nesh system, one above the other. The subjects wore, as viewing spectacles, metallic rims used by ophthalmologists to determine the most suitable correcting lenses or prisms for their patients. Here, prisms were inserted in the rims, one with the base up for one eye, the other with the base down for the other. In our previous work [9], a stereoscopic stimulus was shown on the screen at 1 Hz alternation frequency. The subject then pushed a mouse button to raise the alternation frequency until fusion, then unstable stereopsis, and finally stable stereopsis occurred. The alternation frequency allowing stable fusion in this ascending mode was recorded. We also recorded the alternation frequency for loss of stable stereopsis in the descending mode. The threshold frequencies determined in the decremental mode were on average lower by 0.5 Hz than those determined in the incremental mode, with a standard deviation=0.2 Hz on the 20 stimuli's averages. We also found that the differences between the two variants of the stereograms with opposite sign disparities were minimal (0.11 Hz in absolute values, with a standard deviation of 0.1 Hz on the 20 stimuli's averages).

In the work presented here, we studied the thresholds for stable stereopsis when either a void interval or a binocular interval was intercalated between two consecutive monocular phases.

In a first step, under strict alternation conditions (no void or binocular interval inserted, as in Figure 1a), we determined the maximum monocular durations that allowed stable stereopsis, which gave us the lowest frequency for stable stereopsis, for instance M=100 ms, meaning that the frequency threshold for stable stereopsis was 5 Hz.

In a second step, we explored the situation where a void interval was intercalated between two monocular presentations (Figure 1b). Usually, this void interval had a disrupting effect on stereopsis. In order to recover stereopsis, we decreased the monocular duration (thereby raising the frequency) until stereopsis was regained. This being achieved and recorded, we increased the void interval and determined the new corresponding maximum monocular duration, and so on, until a maximum void interval Vmax was reached at which stereopsis could not be achieved, for any duration of monocular presentation.

In a third step, we explored the situation where a binocular interval was intercalated between two monocular presentations (Figure 1c). Starting with the monocular duration that was determined for the no interval condition (for instance, 100 ms), we inserted a binocular interval between two consecutive monocular presentations, and increased the monocular duration (thus decreasing the alternation frequency) until stable stereopsis broke down. The relationship between binocular intervals and their corresponding monocular durations was strikingly non-linear. This was our main result, documented and discussed in this contribution.

In every case, whenever duration was changed (monocular, void or binocular) the disparity sign was reversed. This was done in order to minimize hysteresis effects from one testing condition to the next (For a discussion of hysteresis effects in stereopsis, see, e.g., [10]). This feature being implemented we checked for each subject and each experimental block that the results were stable upon repetition, as in [9] (data not shown).

Each subject practised on a simple stereogram (a disk behind or in front of a surrounding ring). If during the training period it appeared that a subject was uncomfortable with the disparities (not enough perceived depth in one case, rivalry in the other) the disparities were adjusted by steps of 25%. Then a complete exploration was performed under the conditions of Figure 1a, then 1b, then 1c. The five blocks were presented in random order, and within each block, the stimuli were presented in random order. For each block, the explorations took around 20 minutes to complete. There were 15 to 20 minutes breaks between the series of tests for one stimulus and the next series. For each subject, testing extended on several days. Our data set consisted of 120 experiments. The complete set is shown in the Supplemental material, Figures S6-S10, and a few representative examples will be shown here in Section 3.3.

General observations

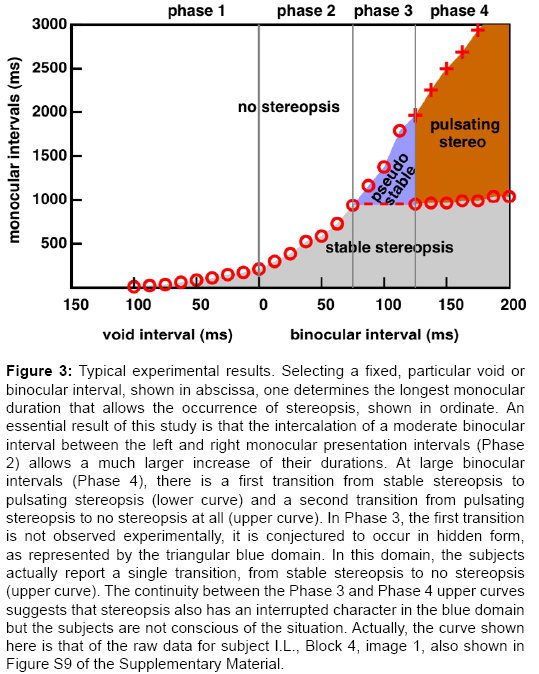
Although there is a wide inter-subject variability, and there are wide quantitative variations in a subject's responses to different stimuli, a typical general pattern is consistently found. It is shown in Figure 3. We discern 4 phases in the subject's responses.

Figure 3: Typical experimental results. Selecting a fixed, particular void or binocular interval, shown in abscissa, one determines the longest monocular duration that allows the occurrence of stereopsis, shown in ordinate. An essential result of this study is that the intercalation of a moderate binocular interval between the left and right monocular presentation intervals (Phase 2) allows a much larger increase of their durations. At large binocular intervals (Phase 4), there is a first transition from stable stereopsis to pulsating stereopsis (lower curve) and a second transition from pulsating stereopsis to no stereopsis at all (upper curve). In Phase 3, the first transition is not observed experimentally, it is conjectured to occur in hidden form, as represented by the triangular blue domain. In this domain, the subjects actually report a single transition, from stable stereopsis to no stereopsis (upper curve). The continuity between the Phase 3 and Phase 4 upper curves suggests that stereopsis also has an interrupted character in the blue domain but the subjects are not conscious of the situation. Actually, the curve shown here is that of the raw data for subject I.L., Block 4, image 1, also shown in Figure S9 of the Supplementary Material.

Phase 1: When there is a strict alternation between the presentation of the left and right images, without a void interval between the two, stereopsis occurs above an alternation frequency f. In previous work [9], we named this minimal value of f required for stereopsis the “alternation frequency threshold”. Here, it will be convenient to present our results using time intervals rather than frequencies. The minimal value of f corresponds to a maximum monocular presentation time M0=1/2f. For instance, a 10 Hz f value is reached by alternating left and right presentations for M0=50 ms each. The subscript “zero” in this notation signals that no void or binocular interval is intercalated between monocular image presentations.

When a void interval is intercalated between two monocular presentations, we move to the left in Figure 3, and stereopsis requires a reduced monocular presentation time, thereby increasing the presentation frequency threshold. As the void interval V is increased, the maximum monocular duration M is reduced, until stereopsis becomes impossible above a certain Vmax value of the void interval. The need for a reduced M when V increases suggests that the limiting factor for the participant is not the amount of data received by each eye, but the time between the reception of the left and right packages.

Phase 2: When a binocular interval of duration B is intercalated between the two monocular phases, the advent of stereopsis tolerates a dramatic lengthening of the monocular phases (preliminary report in [11]). This is observed up to a “bifurcation point”, at abscissa Bbif=75 ms in the case of Figure 3. This 75 ms binocular interval allows the corresponding monocular phase Mbif to last almost an entire second. This is ten times longer than the longest separation between the left and right information streams (Vmax) found in Phase 1.

Our hypothesis is that extending the binocular presentation time allows the consolidation, in a memory store, of the information received, so that the stereoscopic 3d interpretation can be maintained in the absence of new input. The 3d interpretation is nevertheless lost after a certain time, we suggest, either because some of the information in the memory store decays, or because the brain surrenders to the obvious fact that the visual input is monocular. At this stage, it is not clear whether the Phase 1 and Phase 2 results obey a single law, or two distinct laws, e.g., whether there is a single concave trend, or two consecutive linear trends. We skip the Phase 3 results, to discuss now the Phase 4 section of the data.

Phase 4: When the binocular interval reaches 125 ms in Figure 3, two types of results are collected. The lower circles represent the longest monocular durations compatible with stable stereopsis. The values are nearly constant, around one second, and they increase minimally as the binocular interval increases. The “bifurcation point” introduced in Phase 2 was chosen as the point horizontally aligned with the lower circles of Phase 4. These circles tell us that after one second of monocular presentation, and whatever the duration of the following binocular interval, stable stereopsis breaks down.

In the domain between the circles and the crosses, the subject reports pulsating stereopsis: he/she experiences an alternation between 3d and 2d perceptions, and nearly always assumes that the 3d perceptions only occur during the binocular presentations.

However, there is a curious, non-trivial aspect in the data, for which we have no explanation yet. Although we do expect that in an alternation of sufficiently long binocular and monocular presentation of the stimuli, the brain would alternate between 3d and 2d interpretations, the existence of the upper curves really say that 3d interpretations disappear completely above a certain duration of the monocular phases. These are the thresholds represented by the crosses. This could be due to some masking effect, as discussed in several domains of visual perception, but not yet in the context of stereo vision.

Phase 3: The results of Phase 3 are paradoxical, and it took us a long time to accept them, and incorporate them into an interpretative framework. There is a single series of results, represented by the circles that are in the continuation of Phase 2 and Phase 4 results. The subjects report stable stereopsis. For instance, one subject might report stable stereopsis with an alternation of 120 ms binocular presentations and 1.8 second monocular presentations! Such long monocular presentation durations seem to be contradicted by the observation of a limit of around 1 second in Phase 4 results. Our tentative resolution of this paradox goes as follows. What we measure in Phase 3, that is in continuity with the upper branch of the Phase 4 data would be data related to pulsating (interrupted) stereopsis, not stable stereopsis. However, the interrupted character of stereopsis would not reach consciousness. Actually, some people, having interpreted a stereogram in depth maintain the depth perception after closing one eye. Ronchi and Mariani [12] investigated the persistence of depth interpretations after occlusion of one eye, the stimulus being, in their study made of a pair of luminous points in a dark room. They found that stereo persistence required a presentation time of at least ten seconds, and decayed in about ten seconds or less. Another interpretation of our phase 3 results with alternating presentations would be that it is a case of change blindness, a phenomenon amply documented in the case of scene perception [13,14]. Stable stereopsis would be represented by the domain under the dashed line, in the lower part of the Phase 3 sections. This dashed line was drawn by interpolation - it does not correspond to any real measurement.

Interpretative framework: In this way, we have a consistent picture of how stereopsis occurs as a function of the durations of the void, monocular, or binocular phases. Before the bifurcation point, there is a single transition from stable stereopsis to no stereopsis. Beyond the bifurcation point, there are two transitions, from stable to pulsating stereopsis, and from pulsating stereopsis to no stereopsis at all. There would be two paradoxical features: (i) when the binocular interval is within a certain range (Phase 3), pulsating stereopsis is not experienced, presumably due to change blindness, and (ii) at large binocular intervals (Phase 4), pulsating stereopsis disappears, presumably due to some kind of masking.

The value of Vmax, the maximum void interval was >130 ms, in 9 out of 120 cases. Its average over the 120 experiments was 92.6 ms, with a standard deviation of 30 and the average of M0 was 226.7 ms with a standard deviation of 104, so M0/Vmax=2.45. The average of the M0/Vmax values over the 120 experiments was 2.47, and the linear correlation coefficient between the two variables was 0.7. If we split the experiments in two groups, one for low complexity stimuli (Blocks 1, 4 and 5, i.e., 72 experiments) and one for high complexity stimuli (Blocks 2 and 3, i.e., 48 experiments), we find some differences. Indeed, the average Vmax was 104.2 ms for low complexity stimuli and 75.3 ms for high complexity stimuli, the average M0's were 239.2 ms and 208.0 ms respectively, and the average M0/Vmax were 2.26 and 2.78 respectively.

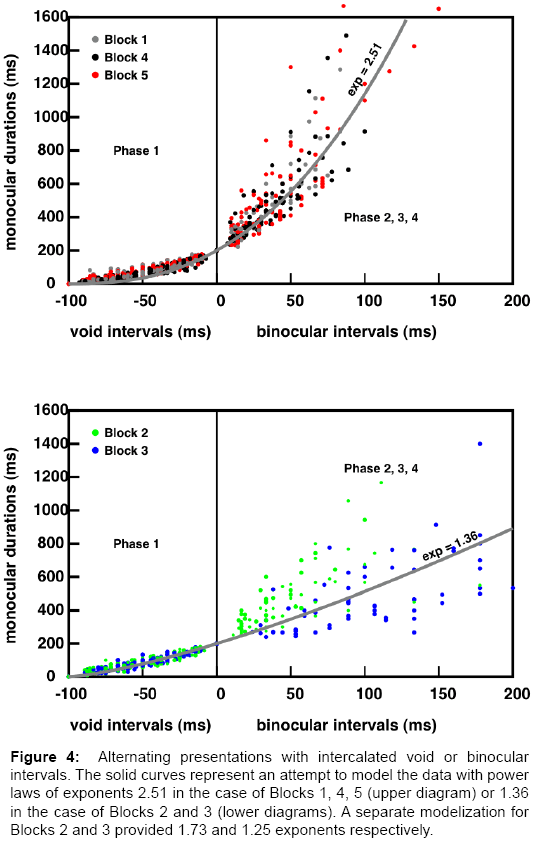
In order to attenuate the dispersion in the data points, we normalized the data in each experiment using multiplicative factors for the abscissas and the ordinates, such that the Vmax values were normalized to 100 ms, and the M0 values were normalized to 200 ms. The normalized results are represented in Figure 4, separately for the stereograms of Blocks 1, 4, 5 (top) and for the stereograms of Blocks 2 and 3 (bottom). With Blocks 1, 4 and 5, the stimuli are defined by a few salient points, while with Blocks 2 and 3, the stimuli are defined by more than 600 points.

Figure 4: Alternating presentations with intercalated void or binocular intervals. The solid curves represent an attempt to model the data with power laws of exponents 2.51 in the case of Blocks 1, 4, 5 (upper diagram) or 1.36 in the case of Blocks 2 and 3 (lower diagrams). A separate modelization for Blocks 2 and 3 provided 1.73 and 1.25 exponents respectively.

Concerning the experiments with void intervals, the vast majority of the data points lie below the straight line that would connect the first to the last point (644 points below, 104 points above), that is, there is clear upward concavity. This upward concavity trend can be seen in most of the 120 individual curves shown in Figures S6-S10 of the supplemental material.

With respect to the experiments with binocular intervals (Phases 2 to 4), the results for Blocks 2 and 3 seem to follow a single trend over the whole range of the void and the binocular intervals. The normalized data can be modelled phenomenologically with a single power law: M=k (Vmax - V) μ for the Phase 1 domain or M=k(B + Vmax)μ, for Phases 2-4. The different equations simply reflect the fact that the B values are counted positively on the abscissas in Figure 3, while the V values run in the opposite direction. By construction, the representative curve is constrained to run through the points {Vmax=-100 ms, 0} and {0, M0=200 ms}.

We found μ=1.36, for Blocks 2 and 3. Note however that there is a clear segregation between the Block 2 and the Block 3 results (see Figure 3) μ exponents determined separately for the two data sets were 1.73 and 1.25 respectively. The results for Blocks 1, 4 and 5 could follow a similar trend, but with a higher power law exponent μ=2.51. Note that Phase 1 part of the curve is more linear than implied by the power law, and it is more similar to the corresponding part for Blocks 2 and 3. We chose to fit the data phenomenological with a power law; there was no theoretical rationale for this choice. The proposed values of μ were determined according to a least square criterion.

What is astounding, in Phase 2, is that a small increment in the binocular interval (say, 25 ms before the bifurcation point) allows the monocular presentation times to increase by ten times that amount. In our preliminary communication [11], we spoke of “the multiplicative effect of small binocular intervals”. In our view, this result implies that during the binocular interval, some 3d calculations are performed and fed into a memory store, in which they remain accessible at a good quality level, for longer monocular durations.

Unstable versus stable stereopsis

In our previous work on alternating presentations [9] we associated to each subject and each stimulus a single parameter, the threshold alternation frequency for reaching stable stereopsis at void interval=0 in synoptophore experiments, or binocular interval=10 ms in the LCD experiments. Here, we have for each subject and each stimulus an exhaustive exploration of stereopsis for a wide range of V's and B's. At small B's (Phase 2), there is a single threshold value separating the stereopsis from the no stereopsis domains. At larger B's (Phase 4), there are two transitions. A first one is between stable stereopsis and unstable stereopsis. The second is between unstable stereopsis and no stereopsis at all. It is this second transition that connects smoothly with the “stable stereopsis versus no stereopsis” curve at smaller B's.

The transition to no stereopsis at all, becomes strange with large binocular intervals (for instance, 200 ms) and long monocular phases (for instance, a few seconds). It seems that the binocular interval alone provides ample time for stereoscopic processing (see, e.g., [15]). We propose that conscious stereoscopic perception is inhibited by the subsequent purely monocular presentation. In order to test this idea, we performed a number of experiments in which the monocular presentations were completely removed. There were only binocular presentations spaced in time, separated by a grey background. In some cases, this resulted in a shift of the curves, but depending on the subject and the stimulus, that shift could take place in either direction (data not shown). We derive from this preliminary exploration the notion that the inputs received outside the binocular presentation intervals may in some cases be used in the stereoscopic calculations (this is the usual interpretation), and that in other cases they may inhibit the development of a conscious stereoscopic interpretation.

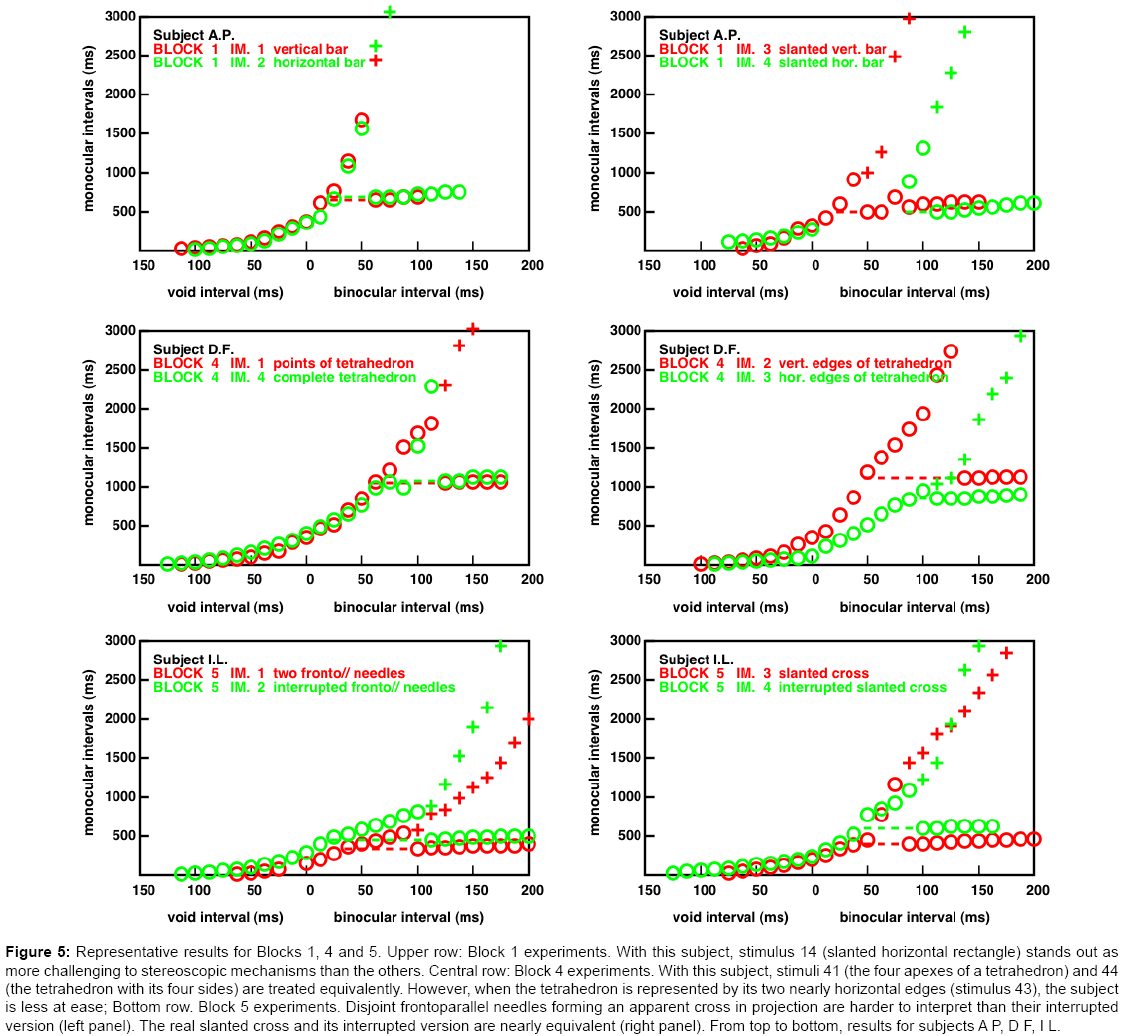
The complete responses recorded in the 120 experiments are shown in the Supplementary Material, Figures S6-S10. In some cases, a subject's responses to two stimuli within a same block are very similar. But there are also cases in which a subject has rather different responses to a pair of closely related stimuli. We will pay attention to the upper curves of the two stimuli. When one is rising faster than the other, this feature implies, in our opinion, that the need to refresh the input is smaller in the first case, and that the first stimulus is easier to deal with. We present now a few examples of a subject's differential responses that may perhaps shed some light on the multiple pathways of stereoscopic interpretations.

Differential subjects responses

An example from Block 1 experiments (Figure 5, top). Here, the subject has very similar responses to the horizontal (Figures 1-12) and the vertical (Figures 1-11) fronto-parallel rectangles. This is expected. There is only position information, at the rectangles' four corners. In sharp contrast, this subject is much more at ease with the slanted vertical rectangle, than with the slanted horizontal one. This can also be explained. In the vertical case, the rectangles' projections appear with different orientations on the two views to be matched. This provides a strong cue (orientation disparity) to slant, although it must be admitted that orientation disparity has been neglected by the stereoscopic community, with rare exceptions (e.g., [16]). Recent work seems to revive the idea [17,18]. In the horizontal case, there is no orientation cue to slant — the cue is provided by the length difference of the rectangle's projections along the horizontal. It thus seems that this subject has no difficulty maintaining orientation (or orientation disparity) information in memory, but that for her, length information quickly fades away.

Figure 5: Representative results for Blocks 1, 4 and 5. Upper row: Block 1 experiments. With this subject, stimulus 14 (slanted horizontal rectangle) stands out as more challenging to stereoscopic mechanisms than the others. Central row: Block 4 experiments. With this subject, stimuli 41 (the four apexes of a tetrahedron) and 44 (the tetrahedron with its four sides) are treated equivalently. However, when the tetrahedron is represented by its two nearly horizontal edges (stimulus 43), the subject is less at ease; Bottom row. Block 5 experiments. Disjoint frontoparallel needles forming an apparent cross in projection are harder to interpret than their interrupted version (left panel). The real slanted cross and its interrupted version are nearly equivalent (right panel). From top to bottom, results for subjects A P, D F, I L.

An example from Block 4 experiments (Figure 5, centre): In the stimuli of Block 4, the figure is always a tetrahedron, but represented in four different ways: by its apexes in stimulus 1, by its four edges in stimulus 4, by its two nearly vertical edges in stimulus 2, and by its two nearly horizontal edges in stimulus 3. For this subject, the results concerning the stimuli represented with a pair of horizontal or vertical edges are entirely in line with those shown for Block 1, in the case of slanted horizontal or vertical rectangles. Because the four apexes of the tetrahedrons are exactly the same, the implication is that point disparity information had been neglected in the horizontal case; the segment length attributes taking precedence.

An example from Block 5 experiments (Figure 5, bottom): Here the stimuli are frontoparallel or slanted crosses, as well as their interrupted versions. The interrupted versions involve four segments in each figure instead of two, so there is more information related to the segments terminators. The two fronto-parallel needles of the first stimulus are at different depths. Therefore, although the four endpoints do match in the left and right figures, the intersections of the two segments in the two projections do not correspond to a real point in space, and they have a vertical disparity in the projections. According to this analysis, the interrupted version should be easier to interpret (as already found on another example in [9]). Here the fronto-parallel needles are always easier to interpret than their uninterrupted counterparts, over the whole range of monocular and binocular intervals. (Figure 6, bottom left). On the other hand, the true slanted cross and its interrupted version is interpreted with about equal ease (Figure 6, bottom right).

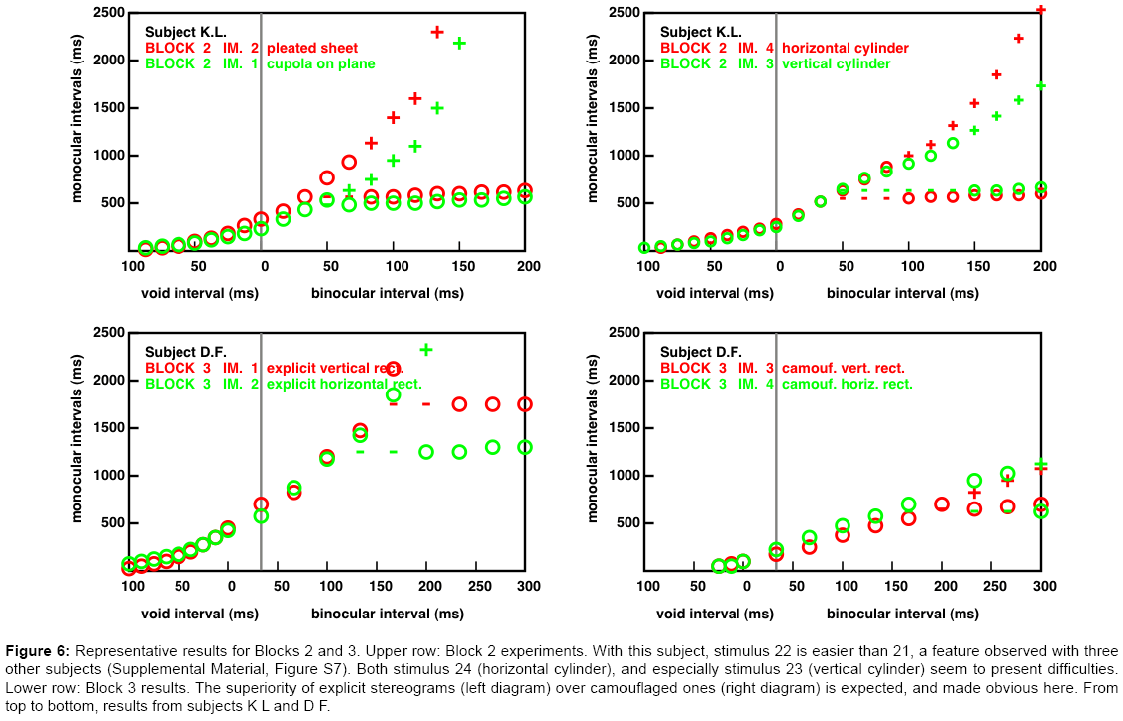
Figure 6: Representative results for Blocks 2 and 3. Upper row: Block 2 experiments. With this subject, stimulus 22 is easier than 21, a feature observed with three other subjects (Supplemental Material, Figure S7). Both stimulus 24 (horizontal cylinder), and especially stimulus 23 (vertical cylinder) seem to present difficulties. Lower row: Block 3 results. The superiority of explicit stereograms (left diagram) over camouflaged ones (right diagram) is expected, and made obvious here. From top to bottom, results from subjects K L and D F.

An example from Block 2 experiments (Figure 6, top): All the stimuli are continuous surfaces, represented in the “random curve stereograms” mode (e.g., [19]). The second stimulus, made of two planar elements, here appears to be easier to interpret than the first, involving a curved surface. In our previous work [9] we noted that some subjects had difficulties with the third stimulus which represents a vertical cylinder. In this stimulus, the disparity field does not change along the vertical direction. In contrast, shear disparities are present in the fourth stimulus, which represents a horizontal cylinder. This feature is known to facilitate stereoscopic interpretations [20].

An example from Block 3 experiments (Figure 6, bottom): As expected, the stereograms representing explicit horizontal or vertical rectangles (left panel) are much easier to interpret than those representing the corresponding camouflaged rectangles (right panel). The origin of the difference between the explicit horizontal and the explicit vertical rectangle is not obvious. The monocular regions are more extended, in the vertical case, and perhaps easier to detect because they are closer to the vertical midline.

Alternation frequency thresholds

In previous work [9] we studied the onset of stereopsis on a set of twenty stimuli close to that of Figure 2, under a strict alternation of monocular presentations of the left and the right images in one set of experiments, and under a similar alternation in another set, but with a 10 ms binocular interval intercalated between monocular presentations, imposed by the viewing apparatus. To each stimulus, we were able to associate a characteristic “alternation frequency threshold”, which was the lowest frequency at which a stereoscopic interpretation emerged. The more difficult a stimulus, the higher the alternation frequency needed to achieve stereopsis. In this way, we could rank the stereograms by difficulty, and sort out various factors that affect the speed of stereoscopic interpretation, including slant, surface curvature, and extraction of monocular regions, camouflage, depth separation, vertical degeneracy, and shape complexities.

It was already clear from earlier work (e.g., [2]) that stereoscopic interpretation requires several alternation cycles to develop. According to one explanation, there would be a certain probability p<1 of success at each half-cycle after the first, so that on average one would need 1 + 1/p half-cycles to achieve a 3d interpretation. However, if the stereoscopic interpretation work is re initiated at each half-cycle, the 3d interpretation would be unstable. This is not the case. Once 3d is obtained, it remains remarkably stable. Therefore, it must be assumed that a 3d interpretation is constructed over several half cycles. Once the 3d representation is obtained, it can be updated and become more and more precise, in agreement with the “coarse to fine” doctrine (reviewed in [21]). It may also be that some information is lost during the monocular presentations, so that the 3d interpretation perceived after a large number of cycles is not the finest possible one. In [9] we reported a number of informal observations pointing in this direction. In several cases, a stereogram presenting a certain amount of complexity was interpreted as a simpler stereogram at a certain alternation frequency, and received a fully correct interpretation at a higher alternation frequency. Thus a slanted bar could be seen as a frontoparallel bar at a certain alternation frequency, and as a fully slanted bar at a higher frequency. (Note that, as reported by van Ee and Erkelens [22] full slant develops gradually.). Furthermore, a surface with a double curvature could be perceived with the main curvature at some alternation frequency, and with both curvatures at a higher frequency [9]. An RDS could be interpreted with a wrong depth sign at one frequency, but nearly always with the correct depth sign at a higher frequency [9].

The phase diagrams

In the work reported here, we sought to investigate in more detail the process of construction of a stereoscopic interpretation over several alternation presentation cycles by intercalating, between the monocular presentation intervals, either a void interval, or a binocular interval. In this way, for each stimulus we obtain a “phase diagram” (Figures 3, 5, 6 and Figures S6-S10 of the Supplemental Material) that contains far more detailed information than the single frequency threshold parameter. In a general fashion, these phase diagrams confirm our proposals, made in [9], about the hierarchies of stereoscopic difficulties. As the intercalated binocular interval increases, we become able to detect larger and larger differences between closely related stimuli (see for instance Figure 5, top right and middle right panels). These differences are often subject-dependent, suggesting that different subjects may use different stereoscopic interpretation pathways. More importantly, our phase diagrams introduce a number of new insights on stereopsis.

Qualitatively, the transition from pulsating stereopsis to no stereopsis observed in Phase 4, upper curve, tells us that stereoscopic interpretations may not reach consciousness in the presence of monocular inputs acting as flatness cues. In contrast, when monocular inputs are not too large, as in Phase 3, they are ignored, and stable instead of pulsating stereopsis is perceived.

Quantitatively, we established how void or binocular intervals, intercalated between alternating monocular phases inhibited or boosted stereopsis. The relationship is clearly non-linear, and it is well modelled phenomenologically by a power law, especially in the Phase 2 domain. This law implies that small binocular intervals allow comparatively large extensions of the monocular presentations. Our result seems to imply that there is a peculiar quality of truly binocular intervals. It is as though they were feeding a memory store with very stable information, while the information obtained from the overlap of live and persistent streams was doomed to fade more rapidly. We do not yet have a definite interpretation of this phenomenon. It could be the case that truly binocular inputs make a fast and precise determination of some 3d parameters possible, while under the overlap conditions, one derives partial information that, in part, needs to be refreshed at each alternation.

Stereopsis and memory

The construction of a 3d percept takes into account both pure stereoscopic calculations, and various texture, occlusion or perspective clues (e.g., [23-25]). Learning could play a role in providing hypotheses that speed up the search for optimal solutions (e.g. [26,27]). Still, it is assumed that the 3d percepts are essentially based on the firing of neurons that take their inputs from the “live” visual streams coming from the two eyes, and not from recent information that was encoded in a short-term memory store. The “online” doctrine for stereopsis was supported by a plethora of work on the Pulfrich phenomenon (e.g., [28-30]). On the other hand, it was reported that persons with eidetic imagery could fuse one member of a RDS seen one day and maintained in memory, with the other member of the pair seen online the next day [31].

The existence of a 3d memory store is supported by a number of informal observations. It is known that the 3d percepts may cover a far more extended area than that being currently captured by the eyes [19,32]. While the eyes move on a stereogram, they grab local information from the sensory data, information that can be processed online and incorporated into a wide 3d interpretation of the stereogram. The 3d percept stays stable, although most of it is taken from some form of short term stereoscopic memory, and there are only brief local captures of disparity information.

Some form of visual memory, beyond stimulus persistence is also implied in studies on binocular rivalry under alternating presentations of the rival stimuli, separated by a void interval, as in Figure 1b. For instance, O'Shea, and Crassini [33] note that “the rivalry mechanism does not need to be “refreshed” for about 300 ms while still producing appreciable rivalry. Referring to the 300 ms “long-term, central, stereoptic persistence” postulated in [34], they conclude that it “is not inconceivable that the rivalry mechanism and the stereoptic mechanism share common input pathways or involve the same units”. For a recent discussion of the relationships between the field of binocular rivalry and that of stereopsis, see [35].

Here, we wish to point out some similarities between stereopsis and scene perception (reviewed in [36]). A well accepted concept in visual memory is that visual information may be maintained in several distinct memory stores, in which it decays at different rates. A new stimulus would begin its life as a detailed representation in a high quality store, then transferred with loss of information in a second quality store, then in a still less precise form in a third quality store [37,38]. Among the new concepts that enrich the picture, let us mention that the coherent visual representation of a scene is much less volatile than the data from which it was constructed [39]. Let us also mention theories of consciousness [40] according to which the representation that is present at one moment in consciousness may be derived from brain areas that work at different processing stages, and we are not aware of the processing level from which the representation was derived (See also [4], for the continuity between monocular and truly binocular interpretations). Our detailed data now provide the beginning of a quantitative insight into the link between stereopsis and memory, and in particular the dynamics of data inclusion and data fading in a hypothetical memory store. We proposed that these dynamics could be represented by a power law, but there will perhaps be a need to separately discuss the fate of different kinds of input, e.g., simple versus complex, with or without oriented elements, with or without curvature, with explicit or camouflaged shapes, with or without disparity discontinuities.

We thank Professor Igor Rabitchev for sharing with us his initial observations on alternating stereoscopy with large intercalated binocular intervals, Robert O'Shea for a critical reading of the manuscript, and Lizard Nada for thoughtful corrections. The Statistical Physics Laboratory is a 'mixed research unit' (UMR8550) of the CNRS. It is associated with UPMC Université Paris 06 and Université Paris Diderot.