The Effective using of Higher Strength Structural Steels in Compression Members
Received: 01-Mar-2014 / Accepted Date: 23-Apr-2014 / Published Date: 27-Apr-2014 DOI: 10.4172/2168-9717.1000125
Abstract
The continuous effort to achieve more efficiency of steel structures results to decrease their weight. Generally, it is accepted that the weight decreasing of steel structures could be achieved mainly by their geometrical and material optimization, using the thin- walled cross-sections and the higher strength steels. The results of numerical analysis of middle and higher strength structural steels using in compression members are presented in the paper. The homogeneous I cross-sections of the members with web slenderness βw = 40, 48, 60, 80, 120; member length L = 3,0; 4,0; 5,0; 6,0 m and structural steels S235, S275, S355, S420 and S460 were assumed. The full theoretical plastic load Npl, local post-critical load Nul and global buckling load Nuy and Nuz for all considered members by the European standards EN 1993-1-1 and EN 1993-1-5 for the design of steel structures were calculated. It is known that these standards have been transformed into national standards of all CEN countries which are generally used from 2010. The effective applying of the higher strength steels on the compressed members taking in consideration their shaping and material optimization is presented in this paper. The obtained numerical results are compared and analysed by choosing technical parameters.
Keywords: Compressed steel members; Homogeneous crosssections; Yield stress; Post-critical behaviour; Local and global buckling load
74666Introduction
The calculation methods and procedures for steel compressed member design, which are applied in the present Standards, are based on the theoretical and experimental research of many researches [1,2]. The certain research of the elastic-plastic load carrying capacity of thin-walled steel members with quasi-homogenous and combined cross-section was realized also by authors of this paper [3,4].
The geometrical design of the member cross-sections is very important for the optimizing of the welded I cross-sections. The essential point for optimizing is the partition of the total section area (A) to the web area (Aw) and the flanges (2Af), which is characterize by the ratio γ = Aw/A. In the case of simple elastic design of member I cross-sections the optimal ratio of sections areas γ≈0,5. Follow on the provided accurate numerical optimizing analysis, it is useful to design the member I cross-sections with local stability flanges and adequate web thickness - slenderness, due to their favourable post-critical behaviour which is allowed by the current codes regulations. Present design fall into the ratio of the cross-section's area γ<0,5 in dependence on the web slenderness βw (βw = d/tw, where d is the depth and tw is the web thickness of the cross-section) and the utilizing rate of the post-critical elastic plastic load-carrying capacity. The utilizing of the higher strength steels looks reasonable at the members subjected mostly to bending, if their lateral buckling is secured. At the same time, it is necessary to point out that in the case of bended members the lateral buckling is usually secured constructively. The load-carrying capacity of compressed members is affected mainly by their global stability. The global stability of compressed members does not depend on the strength, therefore the using of more expensive higher strength steels is not so clear as in case of the bended members. The global stability and related buckling load-carrying capacity of the compressed members seriously depends on their bending and torsion rigidity. Therefore, the efficiency of higher strength steels applying is substantially influenced also by their geometrical - shaping optimization. Economic is not the unique reason to address the shape optimization of steel structures. Raw materials savings - and in a broader sense - sustainability issues are driving factors as well for this work.
Numerical Study
With accordance to the purpose of this paper, for the proposal of this numerical study were used an chosen groups of the welded compressed members joint supported on both sides with different I cross-sections, but suitable related geometrical sizes according to the Figure 1 and Table 1. The analysed cross-sections of all members have had the same sectional area A = 11520 mm2, section depth h = 512 mm, web depth d = 480 mm and the thickness of the flanges tf = 16 mm. The variable parameters were web thickness and flange's width [5,6]. The web thickness tw was varying (tw = 4,6,8,10,12 mm) in dependence of web slenderness βw. The flange's width b was varying (b = 180,210,240,270 and 300 mm) in dependence of web thickness tw. The sectional area of the web Aw and sectional area of the flanges Af were automatically changed.
| Members | A (mm2) | h (mm) | b (mm) | tf (mm) | d (mm) | tw (mm) | Af (mm2) | Aw (mm2) | βw | βf | γ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A (1,2,3,4,5) | 180 | 12 | 2280 | 5700 | 40 | 5,25 | 0,500 | ||||
| B (1,2,3,4,5) | 210 | 10 | 3360 | 4800 | 48 | 6,25 | 0,417 | ||||
| C (1,2,3,4,5) | 11520 | 512 | 240 | 16 | 480 | 8 | 3840 | 3840 | 60 | 7,25 | 0,333 |
| D (1,2,3,4,5) | 270 | 6 | 4320 | 2880 | 80 | 8,25 | 0,250 | ||||
| E (1,2,3,4,5) | 300 | 4 | 4800 | 1920 | 120 | 9,25 | 0,167 |
Table 1: Geometrical dimensions and characteristics of member cross-sections.
According used variation a different web slenderness βw (from 40 to 120) and different ratios of sectional areas γ (from 0,500 to 0,167) were achieved for the individual cross-sections. The web slenderness βw were adjusted in order to show the markedly impact of the local stability and the load-carrying capacity of the analysed compressed members. On the other hand, the slenderness of the compressed flanges βf was adjusted locally stable. From the point of view of the cross-section material of all groups were considered all basic structural steels: S235(1), S275(2), S355(3), S420(4) and S460(5). For the individual geometrical cross-section groups (A,B,C,D,E) and material cross-section groups (1,2,3,4,5) finally were adjusted 4 different lengths of members L (L = 3, 4, 5 and 6 m), Table 2.
| Members | fy (MPa) | L (m) | λy | λz |
|---|---|---|---|---|
| AS (1,2,3,4,5) | 235,275, 355, 420, 460 | 3,4,5,6 | from 12,21 to 29,69 | from 162,01 to 35,71 |
| BS (1,2,3,4,5) | ||||
| CS (1,2,3,4,5) | ||||
| DS (1,2,3,4,5) | ||||
| ES (1,2,3,4,5) |
Table 2: Member`s material and geometrical characteristics.
The slenderness βw is increased by the intentional modification of the web thicknesses tw. The rigidity of the cross-sections is increased by both axes (y, z) at the same time, by the relative regrouping of the web area with the flanges and the increasing of the flange's area. The global buckling load-carrying capacity of the members is increased, especially the load-carrying capacity at the more weak rigidity plane (z). By the increasing of the strength, respectively increasing of the steel yield strength, the local and global buckling load-carrying capacity of the members is increased, with dependence on the member's length L and related stable impacts; these are characterized by their slenderness λy and λz, (Table 2).
The applying of the intentional modification, a total set of 100 compressed members with various geometrical dimensions and strength characteristics were achieved. This enables, with accordance of the main goal, the complex analysis of the compressed steel member design efficiency. For such set of compressed steel members, sequentially according to the methods of European standards EN 1993-1-1 and EN 1993-1-5, the theoretical limit loads Npl,EN, Nul,EN, Nuy,EN and Nuz,EN were calculated. The members limit loads Npl,EN and Nul,EN, and their ratio Npl,EN/Nul,EN are presented in the Table 3.
| Members | Npl,EN(kN) | Nul,EN(kN) | Npl,EN/Nul, EN | Members | Npl,EN(kN) | Nul,EN(kN) | Npl,EN/Nul,EN |
|---|---|---|---|---|---|---|---|
| AS1 | 2707,20 | 2707,2 | 1,000 | CS4 | 4089,60 | 3583,3 | 1,141 |
| AS2 | 2707,20 | 2567,3 | 1,054 | CS5 | 4089,60 | 3648,5 | 1,121 |
| AS3 | 2707,20 | 2481,8 | 1,091 | DS1 | 4838,40 | 4390,0 | 1,102 |
| AS4 | 2707,20 | 2436,3 | 1,111 | DS2 | 4838,40 | 4260,7 | 1,136 |
| AS5 | 2707,20 | 2447,5 | 1,106 | DS3 | 4838,40 | 4190,7 | 1,155 |
| BS1 | 3168,68 | 3063,9 | 1,034 | DS4 | 4838,40 | 4196,7 | 1,153 |
| BS2 | 3168,68 | 2945,3 | 1,076 | DS5 | 4838,40 | 4295,6 | 1,126 |
| BS3 | 3168,68 | 2858,9 | 1,108 | ES1 | 5299,20 | 4740,1 | 1,118 |
| BS4 | 3168,68 | 2821,2 | 1,123 | ES2 | 5299,20 | 4612,6 | 1,149 |
| BS5 | 3168,68 | 2849,0 | 1,112 | ES3 | 5299,20 | 4551,1 | 1,164 |
| CS1 | 4089,60 | 3808,2 | 1,074 | ES4 | 5299,20 | 4572,3 | 1,159 |
| CS2 | 4089,60 | 3679,8 | 1,111 | ES5 | 5299,20 | 4692,9 | 1,129 |
| CS3 | 4089,60 | 3599,3 | 1,136 |
Table 3: Limit loads Npl,EN and Nul,EN for considered compressed members.
The global buckling load-carrying capacity Nu,y,EN and Nu,z,EN of the members in dependence of the length L are calculated by considered standards and presented in the Table 4.
| Members | L = 3,0 m Nu,yEN (kN) |
L = 3,0 m Nu,z,EN (kN) |
L = 4,0 m Nu,yEN (kN) |
L = 4,0 m Nu,z,EN (kN) |
L = 5,0 m Nu,yEN (kN) |
L = 5,0 m Nu,z,EN (kN) |
L = 6,0 m Nu,yEN (kN) |
L = 6,0 m Nu,z,EN (kN) |
|---|---|---|---|---|---|---|---|---|
| AS1 | 2676,11 | 1675,31 | 2667,01 | 1235,21 | 2616,98 | 905,87 | 2565,87 | 679,59 |
| AS2 | 2567,28 | 1933,15 | 2567,28 | 1584,54 | 2529,80 | 1257,14 | 2485,18 | 989,79 |
| AS3 | 2481,76 | 2067,49 | 2481,76 | 1813,55 | 2460,27 | 1545,85 | 2420,40 | 1289,87 |
| AS4 | 2436,27 | 2152,49 | 2436,27 | 1959,35 | 2425,09 | 1750,62 | 2388,09 | 1534,04 |
| AS5 | 2447,53 | 2240,70 | 2447,53 | 2080,77 | 2441,09 | 1909,26 | 2404,94 | 1726,96 |
| BS1 | 3063,86 | 1823,08 | 3040,13 | 1313,84 | 2979,24 | 950,85 | 2916,70 | 708,19 |
| BS2 | 2945,35 | 2146,26 | 2940,56 | 1722,24 | 2886,89 | 1341,22 | 2832,18 | 1042,83 |
| BS3 | 2858,89 | 2326,84 | 2858,89 | 2009,59 | 2819,15 | 1682,07 | 2769,91 | 1380,65 |
| BS4 | 2821,21 | 2446,84 | 2821,21 | 2202,45 | 2793,00 | 1939,09 | 2746,85 | 1671,68 |
| BS5 | 2849,02 | 2566,79 | 2849,02 | 2362,87 | 2825,36 | 2142,97 | 2779,81 | 1911,02 |
| CS1 | 3808,16 | 2071,05 | 3750,30 | 1442,09 | 3666,67 | 1024,71 | 3579,96 | 755,79 |
| CS2 | 3679,83 | 2522,90 | 3646,98 | 1951,08 | 3572,65 | 1476,52 | 3496,19 | 1127,76 |
| CS3 | 3599,29 | 2803,66 | 3583,62 | 2350,66 | 3515,41 | 1905,96 | 3445,64 | 1524,53 |
| CS4 | 3583,28 | 3001,18 | 3577,67 | 2641,87 | 3512,43 | 2261,54 | 3445,93 | 1894,71 |
| CS5 | 3648,52 | 3189,76 | 3646,26 | 2885,26 | 3580,75 | 2556,52 | 3514,04 | 2219,39 |
| DS1 | 4390,01 | 2238,51 | 4300,28 | 1526,95 | 4197,21 | 1073,99 | 4089,55 | 787,89 |
| DS2 | 4260,68 | 2789,48 | 4200,29 | 2103,24 | 4107,96 | 1564,28 | 4012,35 | 1182,79 |
| DS3 | 4190,69 | 3155,69 | 4149,77 | 2586,69 | 4064,15 | 2052,27 | 3975,99 | 1615,83 |
| DS4 | 4196,74 | 3421,54 | 4166,37 | 2958,43 | 4083,55 | 2479,50 | 3998,54 | 2037,50 |
| DS5 | 4295,57 | 3669,71 | 4267,24 | 3271,99 | 4183,22 | 2845,91 | 4097,05 | 2422,25 |
| ES1 | 4740,13 | 2330,14 | 4629,15 | 1573,00 | 4513,68 | 1100,86 | 4392,57 | 805,50 |
| ES2 | 4612,63 | 2938,96 | 4533,37 | 2185,51 | 4429,44 | 1611,20 | 4321,38 | 1212,24 |
| ES3 | 4551,10 | 3358,44 | 4492,46 | 2716,78 | 4395,50 | 2130,30 | 4295,27 | 1663,88 |
| ES4 | 4572,27 | 3668,03 | 4524,19 | 3137,22 | 4429,82 | 2597,53 | 4332,56 | 2112,49 |
| ES5 | 4692,87 | 3954,18 | 4645,69 | 3494,44 | 4549,44 | 3005,79 | 4450,29 | 2530,00 |
Table 4: Global buckling loads Nuy,EN and Nuz,EN for considered compressed members.
The calculated limit loads Npl,EN, Nul,EN, Nuy,EN and Nuz,EN can be explained as:
• Npl,EN is plastic load, provided the full compactness of the cross-sections and members.
• Nul,EN is local elastic load-carrying capacity, taking in consideration the impacts of buckling and post-critical behavior of the slenderness webs in the elastic stage.
• Nuy,EN is global buckling load-carrying capacity related to the axes y-y, taking in consideration the impacts of local buckling and the global buckling of members in the elastic stage.
• Nuz,EN is global buckling load-carrying capacity related to the axes z-z, taking in consideration the impacts of local buckling and the global buckling of members in the elastic stage.
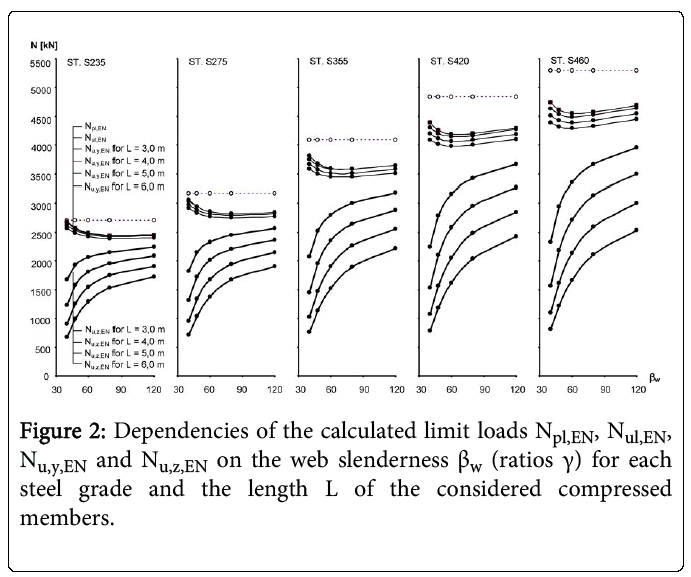
The relative values Npl,EN/Nul,EN characterizing the unfavourable buckling effect of the web through the slenderness βw, but also the favourable effect of partition the cross-section area to web and flanges through ratio γ. Even, the favourable effect of the partition of the cross-section area to web and flanges predominates in the case of higher slenderness webs βw.
Based on the obtained results, it is possible to assign a cross-section characterized by the web slenderness βw and ratio γ for each steel grade. This cross-section responds with the maximum value of ratio Npl,EN/Nul,EN and also with the minimum local load-carrying capacity Nul,EN. By the steel strength increasing, the ratio Npl,EN/Nul,EN is also increasing, but not significantly. For example the maximal value of this ratio for S235 is 1,111 (AS4), and for S460 is 1,164 (ES3).
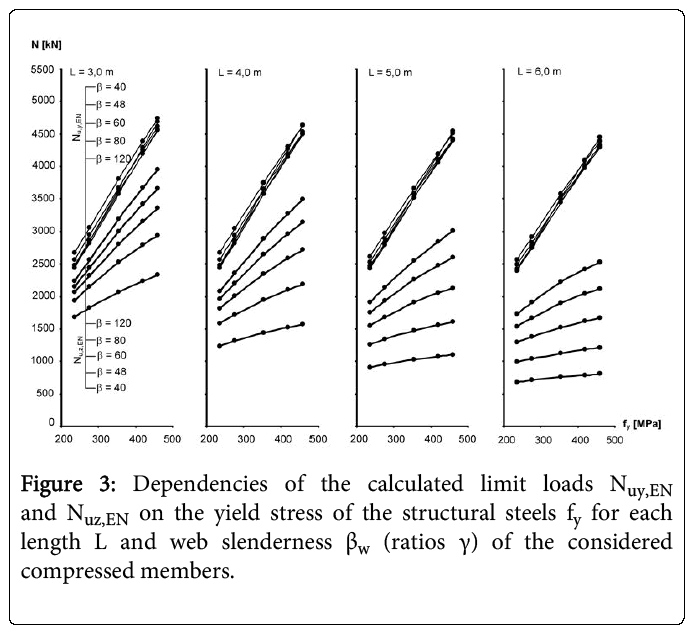
The graphical evaluation and comparing of the limit loads Npl,EN, Nul,EN, Nuy,EN and Nuz,EN of all members, in dependence on the steel strength, web slenderness βw (ratio γ) and length L, is clearly done on the following Figures 2 and 3. Tables 3 and 4, as well as the Figures 2 and 3, present complete information about the effect of the all determining design parameters for each limit loads, respectively load-carrying capacity of the considered thin-walled steel members.
The effect of web slenderness βw and sectional areas ratios γ on the local load-carrying capacity of the compressed members Nul,EN was proved. Generally, the effect of web slenderness βw, could be effectively reduced by suitable distribution of the total cross-sectional area A to the web and flanges. From a certain ratio γ, the local load-carrying capacity of the compressed members is even increased with the increasing of the web slenderness βw.
Then, it is possible to state, that by suitable distribution of the total cross-sectional area A, it is advisable and favourable to design the cross-sections of the compressed members with a thin web. The global buckling load-carrying capacity of the compressed members Nu,y,EN and Nu,z,EN are effected essentially by their slenderness λy and λz. The effects of the web slenderness βw and the cross-section area ratio γ on the global buckling carrying capacity of the compressed members are decreased by the increasing of the slenderness λy and λz. However, by suitable distribution of the global cross-sectional area A to the web and flanges, the slenderness λy and primarily λz could be reduced. In the case of higher slenderness λy and λz, using of the higher strength steel is less effective till ineffective.
Conclusion
The overall economy of steel structures depends on their final prices, but these prices are affected by more actual economic relations, interests and conditions. Therefore, the paper does not deal with economical assessment. The efficiency of cross-section optimization and higher strength structural steels using in compression members is characterized and analysed by equivalent technical parameters. The results of the realized numerical study can be summarized as follows:
• The effect of web slenderness βw and sectional areas ratios γ on compressed members local load-carrying capacity Nul,EN was proved.
• Compressed members ultimate load Npl,EN depends only on sectional area and material strength.
• The ultimate loads Npl,EN are raised by increasing of the material strength, but this is just theoretical respectively comparative loads.
• The effects of web slenderness βw and cross-section area ratio γ on the global buckling carrying capacity of compressed members are decreased by increasing of slenderness λy and λz.
• Global cross-sectional area distribution the slenderness λy and primarily λz could be reduced.
• In case of higher slenderness λy and λz, using of higher strength steel is ineffective.
Acknowledgements
The results are within a matter of VSTE project: 7 Framework programme Transforum.
References
- Shi G, Wang Y, Shi Y (2009) Behavior of high strengthsteel columns under axial compression. Journal of Building Structures.
- Zhang Y, Gou M, Li N, Liang CH (2010) Research on overallstability of axially compressed member of high strength steel. Steel Construction.
- Juhas P, Al Ali M, Kokorudová Z (2008) The elastic-plastic load carrying capacity ofthin walled steel members with quasi-homogenous and combined cross-sections. Journal of Civil Engineering: 7-18.
- Juhás P, Al Ali M, Kokorudová Z (2009) Local stability andcarrying capacity of thin-walled compressed members. Challenges, opportunitiesand solutions in structural engineering: 149-155.
- (2005) Eurocode 3: Design of steel structures – Part 1-1:General rules and rules for buildings.European Standard Norme EuropeenneEuropaische Norm.
- (2006) Eurocode 3: Design of steel structures – Part 1-5:Plated structural elements. European Standard Norme Europeenne EuropaischeNorm.
Citation: Juhas P, Senitkova I (2014) The Effective using of Higher Strength Structural Steels in Compression Members. J Archit Eng Tech 3: 125. DOI: 10.4172/2168-9717.1000125
Copyright: ©2014 Juhas P, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Recommended Journals
Open Access Journals
Article Tools
Article Usage
- Total views: 15211
- [From(publication date): 6-2014 - Aug 19, 2025]
- Breakdown by view type
- HTML page views: 10542
- PDF downloads: 4669