Yield Stress of Bentonite Dispersions

Petroleum Engineering Program, Texas A&M at Qatar, Qatar

*Corresponding Author:

Vassilios C Kelessidis
Adjunct Professor, Petroleum Engineering Program
Texas A&M at Qatar, Qatar
Tel: +974-33321413
E-mail: vassilios.kelessidis@qatar.tamu.edu

Received date: November 14, 2016; Accepted date: December 08, 2016; Published date: December 15, 2016

Citation: Kelessidis VC (2017) Yield Stress of Bentonite Dispersions. Rheol: open access 1:101.

Copyright: © 2017 Kelessidis VC. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Visit for more related articles at Rheology: Open Access

Abstract

We review the factors affecting the yield stress of water dispersions of the wonder material, bentonite. Despite the multitude of applications and its wide use in industry, we still do not have adequate models which enable the prediction of the yield stress of these dispersions, which will allow the manufacturing of fluids with made to order properties. Concentration increases the yield stress of these dispersions according to an approximate power of 3.0, but modeling suggests an exponent of 2.0. pH of the suspension gives maxima and minima; however the results are inconclusive regarding their location. The presence of electrolytes decreases the yield stress of these suspensions but a concrete model to predict the yield stress is yet to be found. Polymers increase the yield stress of the suspensions except at initial low concentrations where a decrease is observed due possibly to a liquefying effect. Very recent reported experimental observations show pictures of flexed bentonite particles in band-type structures in co-existence with isolated bentonite platelets. An analysis is presented which attempts to bring some additional light into the development of the yield stress of these bentonite dispersions.

Keywords

Bentonite; Montmorillonite; Rheology; Yield stress.

Introduction

Bentonite is clay material. Clays are naturally occurring, and they are the most abundant surface minerals on earth, constituting approximately 40% of earth’s crust. They were formed in various ways such as, weathering product of volcanic ash, tuff or other rocks, a hydrothermal product, and as a diagenetic product in ocean basins. Bentonites have a multitude of applications because of their surface activity. Applications include among others, ceramics, paper industry, building materials. Lagaly and Ziesmer [1] distinguish between large volume applications, which include, foundry moulding sands, oil well drilling, pelletizing iron ore, sealing materials and civil engineering applications, and small volume applications which include paints, adhesives (in asphaltic materials and latex), for pharmaceutical uses, in cosmetics, as filling materials and for water (and wine) purification. New trends encompass porous hetero-structures, nanoparticle engineering and nanocomposites [2].

Bentonite was named after the location it was mined, Fort Benton, Wyoming, in USA. It is composed mainly of smectite clay minerals and it is these minerals that give the unique characteristics of water dispersions of bentonite because of their high specific surfaces, great swelling abilities and ion-exchange properties.

Bentonite dispersions gel when left undisturbed and it is this property that makes bentonite valuable to many industries. For example, it is valuable to the drilling industry because the water dispersion of bentonite can support and transfer rock cuttings from the bottom of the hole to the surface. Furthermore, bentonite reduces water loss into permeable formations by forming a filter cake of low permeability on the walls of the borehole.

Rheology and transport properties of bentonite dispersions are of significant importance to many industries. If the viscosity of the dispersion could be reduced at constant concentration, transportation costs could be reduced [3]. On the other hand, the state and the stability of bentonite suspensions at modest to high concentrations is often assessed by rheology, because it aids understanding interparticle interactions of charged particles. This then provides means to relate micro-cosmos (particle-to-particle and particle-to-liquid interactions) to macro-cosmos (rheology) [4-6].

The rheological behavior of bentonite dispersions depends on, the concentration of clay particles, the pH of the suspension, the presence of ions (particularly electrolytes) the temperature, the particle size, as well as the particle shape and the particle size distribution, any hydrodynamic interactions, Brownian motion and inter-particle forces. Particle-particle association or dissociation determines the flow state of the suspension. Bentonite suspensions exhibit non-Newtonian rheological behavior, which should be modeled as yield-pseudoplastic fluids. These suspensions show also gelation and thixotropy [7].

The shear thinning behavior, defined as the reduction of viscosity with increasing shearing, is often associated with changes in the internal structure. It occurs because of microstructural transition from a state dominated by thermal Brownian motion, occurring normally at low shear rates, to a state where hydrodynamics balance thermal forces at high shear rates [8]. If attractive forces prevail, collisions between particles lead to formation of agglomerates. At low shear rates, liquid within the agglomerate structures is immobilized and hence, overall viscosity is high. At higher shear rates, there is a break up of the flocs and of agglomerates, releasing the trapped liquid thus reducing viscosity. Furthermore, particles align in favorable structures, like layers or strings, thus reducing energy dissipation by shear [9,10].

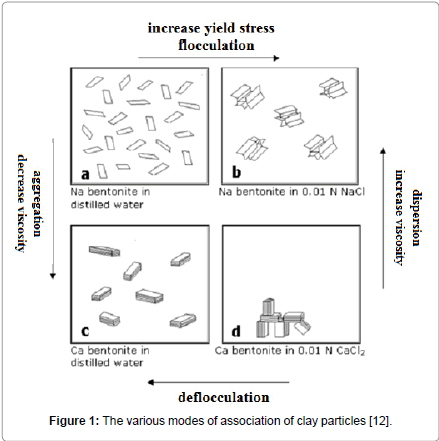
There are many terms in use which describe the ‘association’ or the ‘dissociation’ of bentonite particles when they exist in water suspensions and these many terms cause significant confusion. For example, ‘association’ of the bentonite particles is referenced as agglomeration, aggregation, coagulation, gelation, flocculation, mutual flocculation, hetero-flocculation, while ‘dissociation’ is referenced as deflocculation, peptization, dispersion, thinning. Some distinction also is made between a coagulated suspension, a suspension destabilized by salts, a flocculated suspension, and a suspension destabilized by polymers [11]. In Figure 1, various modes of bentonite platelet association or dissociation is depicted schematically, depending on the major cation present (Na⁺ or Ca⁺⁺) and the presence or not of salt.

Figure 1: The various modes of association of clay particles [12].

Extensive research has been performed on the factors affecting the rheology of bentonite suspensions and while a good understanding exists on their flow behavior, there is still no consensus on the mechanisms of viscosity enhancement and development of gelation of such dispersions.

The unique characteristics of bentonite dispersions make them very useful in a variety of industries in different flow situations, thus there has been always great need to understand the rheology of bentonite dispersions despite the many past research efforts. One of the most important rheological parameters of these dispersions is the yield stress, which is, the required initial stress so that flow will be initiated. In this paper we present the flow characteristics of bentonite dispersions, discuss the parameters affecting their rheological behavior and present modeling aspects and plausible explanations for the yield stress development of these dispersions.

Bentonite characteristics

Smectites, the major clay minerals found in bentonite, are a group of minerals which have common similarities; however, they vary in chemical composition. These minerals are layered-silicates, also described as phyllosilicates (from the Greek word φύλλο - phyllo=leaflike). The building elements of the smectite structures are the two Sioxygen tetrahedral sheets sandwiching one Al-oxygen octahedral sheet which is linked to the two sheets through shared oxygen atoms, hence the term, 2:1 layer structures, is often used. The minerals included in the smectite group are montmorillonite, beidellite, hectorite, which belong to dioctahedral group, i.e., two of the three octahedral sites are occupied, and nontronite and saponite which belong to the trioctahedral group, where all three octahedral sites are occupied [13]. Many times, though, the terms montmorillonite and smectite are used interchangeably because montmorillonite is normally the most abundant mineral found in bentonite. Montmorillonite has the theoretical formula:

Montmorillonite elements, called platelets, are about 1 nm thick. The lateral dimensions can be up to 1000 nm (Figure 2). The three layers of the platelet are held together by the interlayer cations which compensate for the negative charge of the faces of the layers. Several of these platelets are stacked one on top of the other and they form tactoids [14].

Figure 2: TEM image of a single platelet of montmorillonite [19].

Both octahedral and tetrahedral cations in the smectite group might be substituted by other cations by isomorphic substitution, i.e., by maintaining the same tetrahedral or octahedral structure. These cations have mostly lower valency and thus, the initially neutral clay sheets will carry a negative charge. As a result, positive charged ions are loosely adsorbed on the surfaces of the platelets to electrically balance the sheets. These readily exchangeable interlayer cations may be hydrated, un-hydrated or they can be complex cations. Depending on the dominant cation in the crystal lattice, bentonites are characterized as sodium bentonite or calcium bentonite.

The crystal structure that is interrupted at the edges can interact with ions in the suspension through physical (electrostatic) adsorption and through specific chemical reactions with the broken bonds. Dissociation of the formed salts gives rise to positive charges while formation of insoluble salts eliminates positive charges. Thus the faces bear a permanent negative charge while the edges are conditionally charged, that is, either positive in acidic environment or negative in alkaline environment [12,15,16]. The pH value at which the charge of the edges changes sign is the isoelectric point (IEP). While there is ambiguity on the exact value of the IEP, it may be taken at values of pH between 5.0 to 7.0 [17,18].

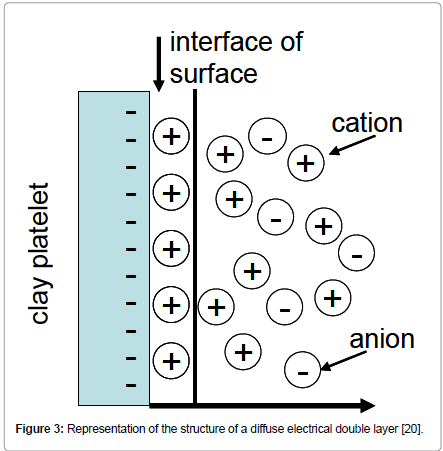
The imbalance in the electrical charge of the surfaces of bentonite particles characterizes the types of interactions with other substances. The presence of positive or negative electrical charge on the particle surface results in the formation of a diffuse electric double layer around the clay sheet, which when combined with the ‘natural’ viscosity of the medium, produces resistance to the movement of clay platelets, giving rise to the ‘electroviscous effect’ (Figure 3).

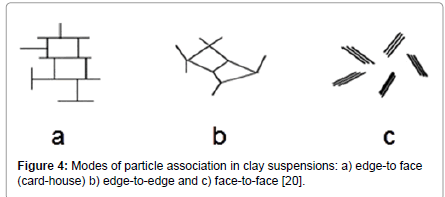
Mainly through observations and measurements of viscosity and less based on theory, it is understood that for bentonite suspensions in water, at concentrations used of approximately 2% to 7% mass, the particles flocculate and form network structures leading to gelation of the suspensions, which is manifested as yield stress. These structures may be caused by edge to face (EF), edge to edge (EE) or face to face (FF) association (Figure 4).

Figure 3: Representation of the structure of a diffuse electrical double layer [20].

Figure 4: Modes of particle association in clay suspensions: a) edge-to face (card-house) b) edge-to-edge and c) face-to-face [20].

Thus, gelation is the process by which individual flocks, or aggregates, form a network transforming the liquid into a gel that upon very soft movement (very low shear) behaves like a solid. Understanding the mechanism of gelation is not only a matter of academic interest but also vital to industry as it will allow control of the many characteristics of gelled systems, for e.g. settling of suspension concentrates, slurry thickening, maintaining stability of suspensions, etc.

When bentonite particles are dispersed in water, the ions are hydrated and the platelets are pushed apart and swelling occurs. The swelling (hydration) process of montmorillonite particles has been studied extensively; however a complete understanding of the swelling process is yet to be accomplished. Researchers are not fully certain whether, upon dispersion in water, the bentonite platelets fully dissociate in single platelets or they form stacks of platelets, commonly now known as tactoids [21], and which resemble a lot like the band-type structures proposed originally by Norrish [22]. For instance, Gray and Darley [12] support complete exfoliation, by making reference to prior work results which showed that Na+-montmorillonite may exfoliate up to individual platelets. Similarly, Segad et al. [23] and Bailey et al. [24] indicate complete exfoliation. On the other hand, Lagaly [25] supports the idea of tactoids formation, particularly in alkaline environment. Such tactoids result from face-to-face association, referenced as heteroflocculation or coagulation or aggregation [26]. Similarly, Zbik et al. [27] and Ali and Randyopadhyay [28], indicate the existence of tactoids. Recently, Mouzon et al. [29] claimed the coexistence of single platelets together with stacks of platelets in specific network structures.

The above disagreements prohibit us to fully understand the mechanisms of the association or of the dissociation of clay platelets, which will aid significantly our efforts to properly model and thus to be able to predict one of the most important rheological properties of these dispersions, the yield stress. Hence, information regarding the size of the bentonite platelets, whether they are a single platelet of about 1 nm thick or they consist of several associated (stacked) particles, is contradictory. Characterization, then, of the gel behavior of such suspensions may vary because of the different degree of exfoliation [30], making thus comparisons or drawing definitive conclusions almost impossible.

Rheological properties

Even dilute water bentonite suspensions show non-Newtonian behavior, exhibiting shear thinning behavior and having also a yield stress. The concentration at which the non-Newtonian behavior is manifested varies depending on the bentonite material used. There have been reports of development of yield stress even at bentonite mass concentrations of less than 2%.

There has been much debated discussion about the existence or not of the yield stress [31]. Our experience has led us to side with several investigators who accept the yield stress as an engineering reality [32- 35], and that it is developed by particular suspensions, such as the ones examined in this work, within the time frame of our observations and of applications.

For years, the rheological model of choice to model flow behavior of bentonite dispersions was the Bingham plastic model, particularly valid at high shear rates. However, this has changed in recent years and now the model of choice, is the Herschel-Bulkley rheological model [36], given by,

where, τ, τ_y are the shear stress and the Herschel Bulkley yield stress, respectively, γ , is the shear rate, and, K, n, are the flow consistency and flow behavior index, respectively. We strongly believe, and we have seen it over and over again, that the best fit to such viscometric data is the Herschel-Bulkley model [37].

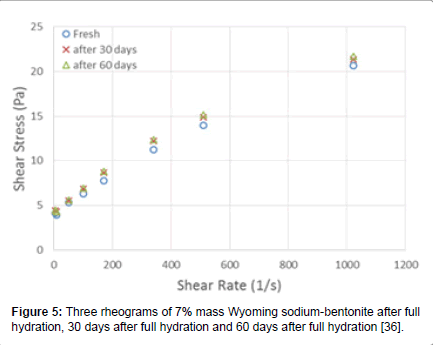
A typical rheogram of 7% mass Wyoming sodium-bentonite dispersion is shown in Figure 5, where we observe the typical yieldpseudoplastic behavior.

Figure 5: Three rheograms of 7% mass Wyoming sodium-bentonite after full hydration, 30 days after full hydration and 60 days after full hydration [36].

It is very interesting to note in Figure 5 the good coincidence of the three rheograms of the same suspension, taken 30 days apart from each other, which is rarely found in relevant publications. Our experience has shown that the rheological results will be consistent when the right preparation procedures of the dispersions are followed, as given by API [37,38], complemented with additional procedures [39]. These procedures require intensive mixing prior to each rheological measurement, which eliminates the inherent thixotropy of these suspensions, thus providing consistent results.

The rheology of the bentonite dispersions depends strongly on the sodium or calcium cation that is prevalent. This issue has not received the required attention that it normally deserves; rather the main distinction is usually made between the two types of bentonites and on the capabilities of the swelling bentonite (sodium-bentonite) or the non-swelling bentonite (calcium-bentonite). However, our experience has shown that there exist differences in rheological behavior.

Abu-Jdayil [40] has shown that all three bentonite dispersions he studied having different concentrations of Na⁺ and Ca⁺⁺ departed from Newtonian behavior at approximately 4% mass concentration. All samples exhibited shear thinning behavior and all developed a yield stress. The point of transition depended strongly on the Na⁺/Ca⁺⁺ ratio. The higher the ratio, the earlier the transition to non-Newtonian behavior was observed. The rheological model was the Herschel- Bulkley model.

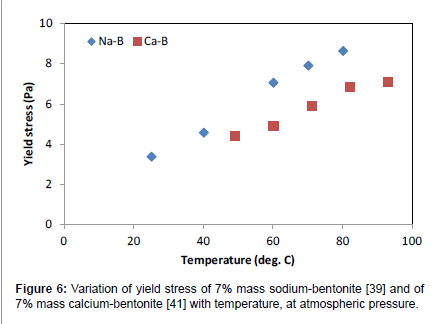
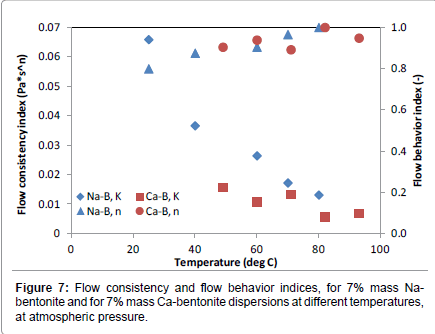
In Figures 6 and 7 the variation of the Herschel-Bulkley rheological parameters are depicted as a function of temperature, for two bentonites, one characterized as sodium bentonite [39] and one characterized as calcium bentonite [41]. For all temperatures studied, sodium bentonite showed higher yield stresses and flow consistency indices, while the flow behavior index hovered between 0.8 and 1.0 for both bentonite types.

Hence, there exist differences in rheological behavior between bentonites with different concentration of sodium and calcium cations. Such differences should be properly identified and possible explanations for such behavior should be sought and given.

Factors affecting rheological properties

There are many factors that affect the rheological properties of water bentonite dispersions. Significant research was devoted on the subject and one can find a wealth of information in published literature. Here we will give a brief overview of this prior work, presenting also results from our past work, in order to pinpoint some of the issues and challenges that we still face when measuring and modeling the rheological behavior of these dispersions. We will be discussing the effects of, bentonite concentration, pH, electrolytes and polymers on the rheological properties of bentonite dispersions. The detrimental effect of temperature on the rheological properties of bentonite dispersions is a very big subject and is beyond the scope of this review. A recent paper [39] addresses this issue.

Effect of bentonite concentration: Higher bentonite concentrations result in higher shear stresses at all shear rates. It is very difficult, though, to scale the effect of solid concentration on the rheology. This is true because even dilute dispersions exhibit non-Newtonian rheological behavior, and thus, there exists no unique scaling rheological parameter (e.g. viscosity), as is the case for hard-sphere dispersion systems. Prior significant work related the Bingham yield stress, τ_B, and sometimes the plastic viscosity, μ_p, to mass, (c), or volumetric, (φ), concentration of bentonite, although it is expected that clay concentration will primarily affect the yield stress.

Figure 6: Variation of yield stress of 7% mass sodium-bentonite [39] and of 7% mass calcium-bentonite [41] with temperature, at atmospheric pressure.

Figure 7: Flow consistency and flow behavior indices, for 7% mass Nabentonite and for 7% mass Ca-bentonite dispersions at different temperatures, at atmospheric pressure.

Van-Olphen [15] early on has fitted bentonite suspension rheological data to the form of,

where, K, c_m, are fitting constants and, c , is the clay mass concentration. Other researchers [42-45] showed a power law dependence of the Bingham yield stress or the Herschel-Bulkley yield stress to the volumetric fraction, �?, or to the mass fraction, c, as,

where, a_i,s=1,4, are constants.

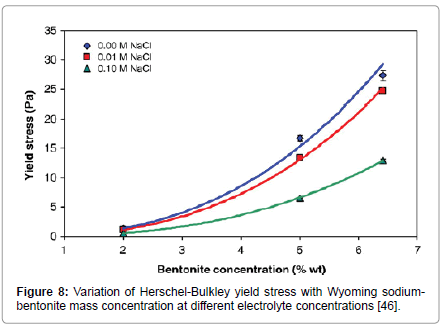
Kelessidis et al. [46] found a similar dependence to eqn. (4) for the Herschel-Bulkley yield stress, as a function of mass content, both for neat suspensions and for suspensions with different electrolyte concentrations (Figure 8). The exponent, a₄, was fairly constant at a value of around 2.7, coinciding with the cubic-power-law of concentration dependence reported previously ([47], for Bingham yield stress; and [48], for Herschel-Bulkley yield stress).

Effect of pH: Suspension pH significantly affects the rheological properties of bentonite dispersions because it influences the mode of particle interaction. Lagaly [25] reported that the rheology of water montmorillonite suspensions (at 4% mass concentration), was highly pH dependent. Shear stress (measured at 94.5s^-1 shear rate) showed a minimum at pH of 6 to 7 increasing both at lower and higher pH values. This behavior was observed for all temperatures studied (from 20 to 60ºC). Presence of electrolytes (0.01 M and 0.1 M NaCl) did not change these trends.

Figure 8: Variation of Herschel-Bulkley yield stress with Wyoming sodiumbentonite mass concentration at different electrolyte concentrations [46].

Benna et al. [17] studied extensively the effect of pH on the rheology of bentonite mixtures, using the vane technique to determine the yield stress. They used Tunisian and Wyoming bentonites after purification, at three, fairly high, concentrations of 12.5% mass, 8.5% mass and 5.5% mass. The general trend observed was similar for all three bentonites. Starting from the natural pH value (neutral to slightly basic) towards acidic values, the yield stress increased and reached a maximum as pH decreased. In highly acidic medium it decreased again. The maximum values occurred at different pH values for the different bentonites. For basic pH environment, the yield stresses reached a minimum over a range of pH of 7 to 11.5 but at very high pH values it increased sharply.

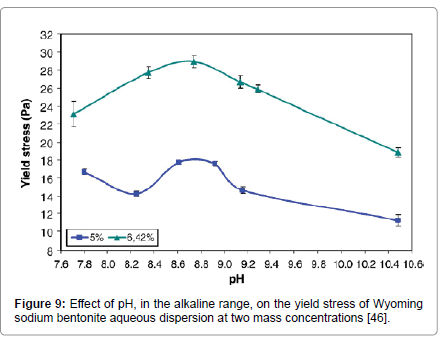
Kelessidis et al. [46] studied the effect of pH in the alkaline range, the environment typically found in drilling applications, of water bentonite dispersions at two mass concentrations of bentonite. Yield stress exhibited a local maximum at the natural (alkaline) pH of the suspensions for both concentrations that were studied (Figure 9); while the suspensions were increasingly more shear thinning at more alkaline pH and the flow consistency index increased with pH.

The described behavior from the mentioned studies does not provide a definitive conclusion on the location of the maxima or minima observed of the yield stress of bentonite dispersions at different pH environments. It could be that the effect depends strongly on the raw material used. Thus, further studies are needed in this area.

Effect of electrolytes: The presence of inorganic salts, and in particular of NaCl, destabilizes aqueous-bentonite dispersions because the electrical double layer, which forms around the clay mineral particles and keeps them in dispersion, is compressed by the cations, allowing the formation of aggregates thus changing the mode of particle association.

The Schulze-Hardy rule [49] states that ‘the coagulative power of a salt is determined by the valency of one of its ions’. The flocculation power is known as the Hofmeister series and the coagulation power of the cations can be ordered as [15],

Van-Olphen [15] studied the effect of NaCl on rheology of clay suspensions and found that the suspensions start from a flocculation state and adding small amounts of NaCl, the Bingham yield stress reaches a minimum, and thus suspension deflocculates. Upon further addition of NaCl, Bingham yield stress increases again, i.e., the system flocculates again.

Luckham and Rossi [20] summarized prior work on the effect of salts on rheological properties of up to 10% mass of sodium montmorillonite suspensions. They found that the suspensions behaved as Bingham plastic and that addition of small amounts of NaCl decreased both yield value and plastic viscosity. With higher amounts of NaCl there was a gradual increase of both yield stress and plastic viscosity.

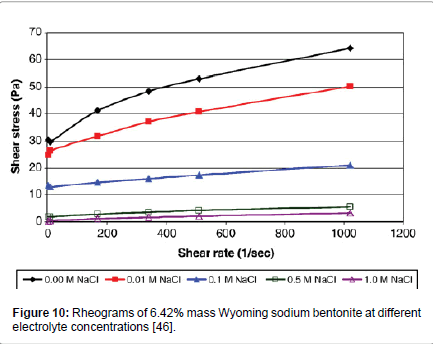
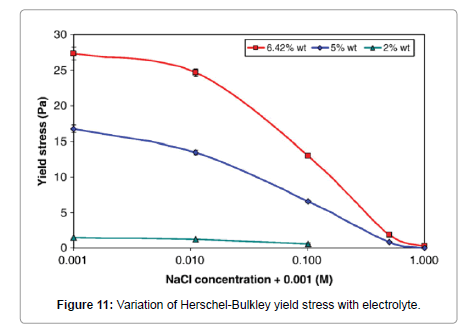
Abu-Jdayil [40] has shown that as the concentration of electrolytes is increased, the apparent viscosity and the yield stress of the three studied bentonites decreased. Similarly, Kelessidis et al. [34] found a significant effect of electrolyte concentration on the shear stresses which were reduced considerably at all shear rates (Figure 10), which in essence, it was an effect of lowering the yield stress of the dispersions (Figure 11).

Figure 9: Effect of pH, in the alkaline range, on the yield stress of Wyoming sodium bentonite aqueous dispersion at two mass concentrations [46].

Figure 10: Rheograms of 6.42% mass Wyoming sodium bentonite at different electrolyte concentrations [46].

Figure 11: Variation of Herschel-Bulkley yield stress with electrolyte.

From these prior studies it is then evident that addition of salt influences the rheological parameters of bentonite dispersions, however, the magnitude of the effect differs among different studies. Kelessidis et al. [46] have attributed these variations to differences in the raw material, as some investigators used commercially sold material, while others purified it. Some investigators use naturally occurring sodium montmorillonite, while others use soda activated montmorillonite. Furthermore, not all studies have covered similar clay concentration ranges. Most importantly, it is expected that preparation procedures should have the most drastic effect on the measured properties as there exists no standard protocol for preparing water bentonite dispersions, a fact also noted previously [39].

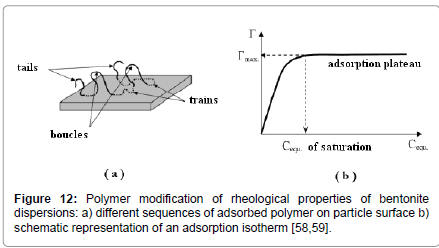
Effect of polymers: Polymers containing acidic or basic groups are added in clay suspensions for a variety of reasons in applications like, water purification [50,51], sewage treatment [52] or flocculation [4]. Non-ionic polymers are often used in oil-well drilling because they inhibit shale dispersion or clay swelling [53-56]. Polymers adsorb onto clay surfaces (Figure 12) thus prohibiting the association of clay particles. Hence, adsorption studies are often carried out first to determine the amounts of polymer adsorbed and the conditions affecting them, followed by rheological measurements to assess the final impact of polymer addition on the stability of the suspensions.

Polymers, such as Carboxyl-Methyl-Cellulose (CMC) or Partially- Hydrolyzed-Polyacrylamide (PHPA) and novel polymers, based on CMC containing poly-ionic cellulose (PAC) [57] were used in suspensions for applications like, drilling fluids, to coat drill cuttings produced from shale formations in order to prevent (inhibit) disintegration. These additives have “arms” with many functional contact points which can react and link with the anionic groups of other polymers and clay structures, providing thus very effective control.

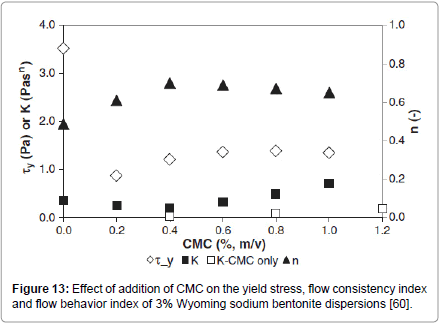
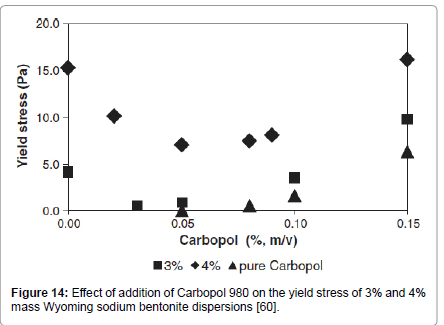
The effect of addition of CMC and of Carbopol 980, on the rheology of Wyoming sodium bentonite suspensions was studied by Kelessidis et al. [60]. Both polymers showed high affinity for adsorption onto bentonite particles following Langmuir isotherms of the L1 type, indicating monolayer adsorption of the polymers onto the surface of the bentonite particles. CMC addition did not affect the yield-power law rheological behaviour of the neat dispersions. The yield stress exhibited a minimum at low CMC concentration and then reached a plateau at about 40% of CMC-free water-bentonite suspension, at the highest CMC concentration tested of 1.0% mass (Figure 13). The decrease of the yield stress upon addition of CMC was attributed by the authors to liquefying effect of the additive.

Addition of Carbopol 980, up to 0.15% mass concentration, resulted also in a minimum and then it evolved in a similar fashion as the pure Carbopol solution (Figure 14).

Figure 12: Polymer modification of rheological properties of bentonite dispersions: a) different sequences of adsorbed polymer on particle surface b) schematic representation of an adsorption isotherm [58,59].

Figure 13: Effect of addition of CMC on the yield stress, flow consistency index and flow behavior index of 3% Wyoming sodium bentonite dispersions [60].

Figure 14: Effect of addition of Carbopol 980 on the yield stress of 3% and 4% mass Wyoming sodium bentonite dispersions [60].

Discussion on the development of yield stress of bentonite dispersions

The various factors affecting the rheological properties of water bentonite dispersions were briefly described above. In order to better understand and explain the effects of all these parameters on the rheology of these dispersions, it is important to understand the development of the yield stress of the neat bentonite dispersions. This means that we need to understand which are the factors which contribute to the development of the yield stress of the neat suspensions, so that appropriate actions can be taken, either to increase or decrease the yield stress, according to the case at hand, with the use of the different additives or according to the prevailing environmental conditions.

It is well understood that the bentonite particles associate or dissociate when they are dispersed in aqueous environment. The question which is raised though is, in an alkaline environment, which is the prevailing association, edge-to-edge (EE), edge-to-face (EF) or face-to-face (FF), when these surfaces are all negatively charged. There are predictions [1] that repulsion forces between edge (-)-to-face (-) (EF) are weaker than face (-)-to-face (-) (FF) repulsion forces, but are they strong enough to force coagulation? It is theorized [15,20] that electrolytes compress the diffuse double layer allowing particles to come closer together so that attractive Van-der-Waals forces could dominate causing coagulation, but it is still uncertain whether this is the mechanism of action.

In many applications, pH of suspensions is alkaline, as for example in drilling fluids, and well above the isoelectric point of bentonite suspensions, which ranges between pH of 5.0 up to pH of 7.0 [17,61,62]. Under such conditions, positive-edge-to-negative-face association should not occur, thus, another attaching mechanism should be found. However, EF association at alkaline pH and specific salt concentrations has been suggested by Permien and Lagaly [63]. Other investigators report and suggest band like structures resulting from FF association which gives larger flakes and stronger gels [20,22,26,62].

Yet another mechanism may be possible, as revealed by some results from scanning electron microscope studies, shown in Figure 15 for bentonite suspensions [46] and in Figure 16 from filter cakes [64] taken with an American Petroleum Institute filter press [37]. What is observed is that the bentonite platelets flex and seem to associate primarily by the EF mode and create structures resembling lenticural pores, very similar to the ones reported previously [65,66] who, however, attributed them to random aggregation of sheets rather than to the EF association appearing in these figures.

Figure 15: SEM of hydrated 6.42% Wyoming bentonite at pH of 9.1 [46].

Figure 16: SEM pictures of API filter cake of bentonite suspensions. 1) 6.42% Zenith (Na⁺ activated calcium bentonite) 2) 6.42% Wyoming (natural Na⁺ bentonite) [64].

Figure 17: TEM picture of 7% mass Wyoming sodium bentonite suspension. The individual platelets are clearly seen as the edges have folded, and one can count approximately 20 platelets (bar size=20 nm), with approximately 1 nm thickness [39].

Figure 18: TEM images of natural montmorillonite: (A) dry Na-montmorillonite samples [23] (B) purified montmorillonite dispersed in water (adapted from [25], taken from [67]).

As the instruments of observation improve, researchers managed to present evidence of the coexistence of single platelets together with stacks of platelets in specific network structures [29]. In Figure 17, we show the TEM image taken from one of our own dried samples of a water dispersion containing 7% mass of Wyoming sodium bentonite [39]. The existence of a tactoid is very evident which consists of approximately 20 platelets, each of almost 1.0 nm-thickness.

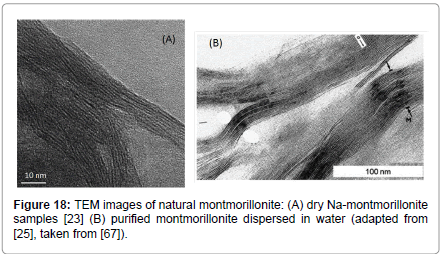
In Figure 18, similar TEM images to that of Figure 17 are shown, exhibiting striking similarities between each other. In Figure 18A, the image of Na-montmorillonite is shown, while in Figure 18B, the image of purified montmorillonite dispersed in water is shown, although the latter do not state the amount and the type of montmorillonite. One can see clearly in all TEM pictures the lamellar structure of sodium montmorillonite, while also identifying the high-aspect ratio and the flexibility of the montmorillonite platelets.

What is not at all evident is the way the platelets associate to each other when dispersed in water, either as single platelets or as tactoids, despite having similar negative charges. A driving force is required to associate similarly charged particles to each other forming network structures which are manifested as yield stress. The determination of this driving force and its function, being long range repulsive or long range attractive, has been the subject of controversy, both from experimental and theoretical points of view [68-72]. Once this is understood, one may have clearer picture of what happens to the particle association both at low as well as at high temperatures.

Researchers in the past have proposed many ways of platelet association, like, no physical contact, house-of-cards, honeycomb, band structures, and so on. Benna et al. [17] stated that, at basic pH values, the interactions between particles could lead to card-house like structures based on repulsion. McBride and Baveye [73] argue that it is the attraction between like-particles, as per Sogami-Ise theory [74], which provides the attraction force that is responsible for the clay particle flocculation even at the basic pH values encountered in many industries, like the drilling fluid industry, although the nature of this attractive force is still elusive.

The network (gelling) structure of clay suspensions may be created from the particular alignment of similarly charged surfaces, as for example edge (-) to face (-) , edge (-) to edge (-) and face (-) to face (-) in an alkaline environment. One should notice that for concentrations of, for e.g., 3.0% to 7.0% mass, a significant amount of clay platelets is present in the suspension meaning that the platelets are crowded and the amount of free water is very limited. The repulsion between similarly charged surfaces may orient them in particular ways so it may create packets of them enclosing water in between, thus forming gel structures. This is very similar to the notion of covoluted volume (excluded volume) of Onsager [75] which explained the strange behavior of colloidal particles having much smaller rotational diffusion coefficient than translational because the volume of the suspension influenced by the particle itself is much larger than the volume of the particle.

In fact, for plate like particles, considered as discs of diameter, d, like the bentonite platelets, the ratio of covolume to particle volume, R, can be approximated by, R= πd/4h, where h is plate thickness. Thus R can be a fairly large number, which is of the order of the ratio of the large to the small particle dimension. Based on the above arguments, it was shown that, a 0.6% mass smectite in water suspension will occupy volumetrically 0.23% of the total suspension volume (if we take the relative density of the clay as 2.6), not counting the electrical double layer (EDL) [73]. However, if one counts the covolume, as proposed to be computed above, using d ≈ 300 nm and h ≈ 1.0 nm, the total solid suspension would be 300 times 0.23, giving 69% of total suspension volume, thus leaving very little room for rotation due to thermal motion. This then may account for the strong inter-particle interaction observed even at very dilute solid concentrations.

We can perform similar calculations for a 7% mass concentration of bentonite suspension, normally used in drilling industry. Sodium bentonite platelets are approximately orthogonal in shape with the large dimension of ~300 nm to 500 nm and the small dimension of ~200 nm to 300 nm. Many researchers have reported a narrow-distribution for thickness of the particles, centered on ~1.0 nm [76,77]. If we take a 500 nm by 300 nm particle, of 1 nm thickness, this will give an equivalent disc diameter of 220 nm. A 7% mass bentonite suspension will occupy volumetrically 2.7% of the total space, and if we compute the covolume as analyzed above, it will give of total solid suspension of 466% of total volume, which is apparently wrong. But this simple computation indicates that there is no possibility of having complete exfoliation of all bentonite particles at such high concentrations. Furthermore, this analysis serves to demonstrate that the free water will be diminishingly small at these conditions. Hence, when there is covolume occurrence the particles are forced to have certain alignments (ordering), resulting thus in the reduction of free energy [73]. Interestingly enough, McBride et al. postulated a phase transition to anisotropic phase from isotropic, at clay concentrations of around 5% mass, for clay particles of 300 nm equivalent diameter.

Frenkel used covolume effects, as suggested by Onsager, to explain the transition between disordered and ordered states. Ordering of colloidal suspensions may give smaller covolume allowing particles to move more freely thus increasing entropy. At first thought this is counter intuitive, as higher entropy is associated with less ordering; but in this particular situation, invoking the covolume approach, the loss of the orientational entropy of the ordered (nematic) phase is more than offset by the increase in translational entropy, due to the more space available to the solids for movement [78]. Hence, ordering is favored because it leads to higher entropy.

This theory could explain the band structures-aggregates of bentonite particles. In Figure 19, the various states of ordering of particles in a suspension driven by entropy are depicted. The structure of plate like particles can be, (a) disordered (isotropic) (Figure 19a) or ordered, taking the shape of (b) nematic (Figure 19b), with preferred orientation but no long range positional order, (c) smectic, (Figure 19c), i.e., one dimensional periodic array or (d) it can be even two dimensional lattice (columnar, Figure 19d) [73,79,80].

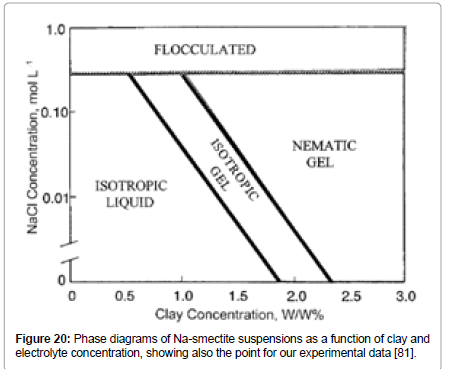
Based on these notions, Gabriel et al. [81] constructed a phase diagram for montmorillonite particles (Figure 20) which shows that for cases of no salt or low salt concentration and with bentonite concentration higher than 2.5% mass concentration, the suspension should be in the region of nematic gel.

Figure 19: Disordered (a) and ordered (b, c, d) structures of plate like particles [73].

Figure 20: Phase diagrams of Na-smectite suspensions as a function of clay and electrolyte concentration, showing also the point for our experimental data [81].

It is very interesting to note that, by means of Monte-Carlo simulations, eight distinct configurations for bentonite platelet charged disks were recognized [72], including nematic and anti-nematic configurations, very much like the ones identified in Figure 19b.

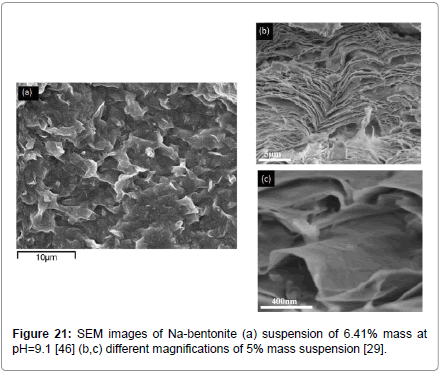
Of course, the above geometrical associations are very idealistic, particularly in view of previous observations [46,64] as well as new insights derived from pictures taken using new sophisticated instruments [29]. Such pictures show that the bentonite particles are in fact very flexible, flexing and stacking in layers and associating, most probably, in a ‘face-to-face’ and ‘edge-to-face’ manner (Figure 21) and they form associations plausibly of Y-type (Figure 22).

Mouzon et al. analysis [29], as well as prior evidence, shows that bentonite platelets form the type of nematic gels which were idealized in Figure 19 [73]. In fact, according to Mouzon et al. [29], the particles create clusters resulting from the mutual repulsion of the platelets, with the repulsion forces creating osmotic pressure which deforms the platelets and forces them to adopt the FF configuration. It was also shown that some of the platelets remain in dispersed state, even at 5% mass concentration and not all platelets had this peculiar flexed FF structure. It is very encouraging that phenomenological modeling which gave structures like the ones shown in Figure 19b are not very far from reality (Figure 22), if one accounts for the flexibility of the bentonite platelets.

At high shear rates the platelets will align with the flow direction and there will be less structure compared to the structured FF arrangement, when there is no flow, offering less resistance. Hence, at high shear rates, one should observe smaller apparent viscosities, and in fact we have seen they become Bingham plastic like. As the shear rate is decreased, moving to smaller shear rates, the particles re-align as per FF of flexed particles and thus offer more resistance to flow due to drag, resulting in an increase of the apparent viscosity. At the limit of no shear rate, the suspension is at rest and the platelets associate mostly as per association types shown in Figure 21 [29,46]. Thus, in order to initiate flow, we need an extra force to have the suspension moving which manifests as yield stress.

It was shown sporadically in the past [82,83] and more systematically recently that as the temperature of the suspension increases, the yield stress increases. It is thus probable that as the temperature increases, the particles in the dispersed state move due to Brownian motion and become also flexed and associate in the FF mode, creating more clusters, thus increasing the yield stress, in accordance with experimental measurements [39].

Figure 21: SEM images of Na-bentonite (a) suspension of 6.41% mass at pH=9.1 [46] (b,c) different magnifications of 5% mass suspension [29].

Figure 22: Association of SWy-2 Na-bentonite platelets at 5% mass concentration, as photographed by cryo-SEM (hence in situ!), at different magnifications: (a) low magnification, (b) high magnification, (c) Y-type associations. One should note the similarities between Figures 21a and 22a [29].

Modelling Aspects

The yield stress of charged particle suspensions arises because of existence of net interparticle attractive forces between the particles which link them in various configurations. Thus, an increase in this net attractive force results in an increase of the yield stress, other factors remaining constant. There have been several attempts to relate yield stress to these interparticle forces but no unique models exist to date. Theoretical or semi-empirical approaches have yet to provide predictions close enough to experimental data. Various explanations exist for this discrepancy like, validity of measurements (6) or, the fact that the nature of the interactions between charged particles in liquid media is not fully understood. One may argue that the DLVO theory [84,85], adequately covers some situations but it cannot account for the full range of forces present. It was shown that even if the extended DLVO theory is used, full account of all applicable forces is not achieved [18]. In fact, the mere situation that a wide range of additional forces has been proposed to fully account for all interparticle forces, shows the long road that our understanding has to cover in order to be able to predict, with reasonable accuracy, the yield stress of such suspensions from modeling of microscopic interactions.

A review of the literature [86-89] suggests that for charged particles of diameter, a, the form of the predictive equation for the yield stress, τ_y, is,

where, ζ, is the zeta potential, �?, is the solid volumetric concentration, and, A,B, are empirical constants. Hence, the yield stress becomes maximum either at the isoelectric point (ζ=0), or at the condition of minimum ζ.

Kelessidis and Maglione [6] used the above equation in the form of,

to predict the yield stress of bentonite dispersions at the isoelectric point. They took certain values for particle diameter, a, for inter-particle distance, h₀, and different values for the Hamaker constant, A_H, because no single value could be found in the literature. They tested eqn. (6) for two types of bentonites and two concentrations. Good matching for one of the bentonites (Zenith bentonite, a treated sodium bentonite) was achieved for a value of Hamaker constant of, A_H=0.04*10^-20 J. Similarly, a good match was found for Wyoming bentonite dispersions, but for a Hamaker constant 2.5 times higher, at A_H,=0.1*10^-20 J. One should note, though, that the values of,A_H, that gave very similar maximum yield stresses to the measured ones, were one to two orders of magnitude lower than the values previously reported [6]. Kelessidis and Maglione [6] finally concluded that eqn. (6) could be a very good starting point to estimate the yield stress of bentonite dispersions, provided that we have available more accurate values, of the Hamaker constant, of the particle diameter and of the particle thickness. These discrepancies coincide with the experimental observations which show a third power dependence of the yield stress to the mass concentration.

The many attempts to relate microscopic colloidal interparticle forces to macroscopic properties like, rheology and in particular the yield stress have not materialized yet for many reasons. It was shown that the yield stress, determined by the vane technique, scales with interparticle forces [86,88]. These interparticle forces involve attractive and repulsive forces at the atomic or molecular scale. The inherent difficulty then, in relating micro-cosmos to macro-cosmos, arises from the fact that in micro-cosmos, the parameters involved are of very small magnitude, for e.g. the values of Hamaker constants are of the order of 10^-20 J. Similarly, Debye length (the distance over which a charge is shielded by the ions in a suspension) is of the order to 10^-10 m. On the other hand, in the macro-cosmos, yield stresses, true and measurable quantities, are mostly of the order of 1.0 to 100.0 Pa, for the bentonite concentrations normally used. Division between two similar very small numbers (for e.g. eqn. 6) could give a result of a large magnitude number, the yield stress. But equally well, errors in the small numbers, even in the 100 to 200% range could go unnoticed. In fact, how can one tell the differences between a Hamaker constant value of, AH ̴ 1.0*10^-20 J, and a value of, A_H ̴ 1.9*10^-20 J? However, when these numbers are used to predict ‘real world’ numbers, like the yield stress, they could produce noticeable errors of the order of 100%.

Conclusion

Aqueous bentonite dispersions exhibit non-Newtonian rheology. The most appropriate model is the yield-pseudoplastic model of Herschel-Bulkley. The yield stress of these dispersions is noticeable for bentonite concentrations as low as 2% mass. The two bentonite types, sodium or calcium bentonite, have been reported to have different rheological parameters at same bentonite concentration.

We discussed the effect of concentration, of pH, of electrolytes and of polymers on the rheology and on the rheological parameters of these bentonite dispersions and mainly the effects on the yield stress. The yield stress increases according to approximately the third power of mass concentration. Suspension pH influences strongly the yield stress, with maxima and minima reported over the full pH range, however there is no consensus regarding the location of the maxima or the minima as well as the corresponding values. The discrepancies can be attributed to the differences in the raw material. Addition of polymers also affects the yield stress of bentonite dispersions. At low concentration there may be a decrease of the yield stress due to a liquefaction effect of the polymer additive but at higher concentrations, yield stress increases with polymer concentration.

There is still ambiguity regarding the type of association or dissociation of bentonite particles and no consensus exist whether complete exfoliation of these particles occurs when they are dispersed in water. Good understanding of the mode of interaction of these particles will enhance our modeling attempts to describe the gelation of these suspensions allowing the prediction of the yield stress, given the environmental conditions. This has been an elusive task and an accomplishment not achieved to date. Recent in-situ images of such dispersions with highly sophisticated instruments lead us to conceive band type associations of flexed bentonite particles with individual platelets also present. Theoretical studies using simulations, assuming though hard disc models, produce structures similar to what the experimental observations reveal. Further work is needed, invoking possibly molecular simulation in confined spaces to bring together the micro-cosmos with the macro-cosmos of bentonite dispersions.

References

1. Lagaly G, Ziesmer S (2003) Colloid chemistry of clay minerals: The coagulation of montmorillonite dispersions. Adv Colloid Interface Sci 100-102: 105-128.
2. Gournis D1, Jankovic L, Maccallini E, Benne D, Rudolf P, et al. (2006) Clay-fulleropyrrolidine nanocomposites. J Am Chem Soc 128: 6154-6163.
3. Kumar P, Kapur PC, Saraf DN (1975) Effect of zeta-potential on apparent viscosity of settling suspensions. Coll Polymer Sci 253: 738-743.
4. Tadros, Tharwat F (1992) Control of stability/flocculation and rheology of concentrated suspensions. Pure & Appl Chern. 64: 1715-1720.
5. Quemada D, Berli C (2002) Energy of interaction in colloids and its implications in rheological modeling. Adv Colloid Interface Sci 98: 51-85.
6. Kelessidis VC, Maglione R (2008) Yield stress of water-bentonite dispersions, colloids and surfaces. A Physicochem Eng Aspects 318: 217-226.
7. Tadros, Tharwat F, (1993) Industrial applications of dispersions. Adv Colloid Interface Sci 46: l-47.
8. Rueb CJ, and CF Zukoski (1998) Rheology of suspensions of weakly attractive particles: Approach to gelation. J Rheol 42: 1451-1476.
9. Hoffman RL (1972) Discontinous and dilatant viscosity behavior in concentrated suspensions I observations of flow instability. Trans Soc Rheol 16: 155-173.
10. Chen LB, Chow MK, Ackerson BJ, Zukofski CF (1994) Rheological and microstructural transitions in colloidal crystals. Langmuir 10: 2817-2829.
11. Harrison G, Franks GV, Tirtaatmadja V, Boger DV (1999) Suspensions and polymers ��? Common links in rheology. Korea-Australian Rheol J 11: 197-218.
12. Gray HCH, Darley GR (1988) Composition and properties of oil ��? well drilling fluids. Gulf Pub Co.
13. Güven N (1988) Hydrous phyllosilicates. Mineralogical Society of America 19.
14. Shomer I, Mingelgrin U (1978) A direct procedure for determining the number of plates in tactoids of smectites: The Na/Ca-montmorillonite case. Clays and Clay Minerals 26: 135-138.
15. Olphen HV (1977) Introduction to clay colloidal chemistry. Wiley New York 2.
16. Tombácz E, Szekeres M (2004) Colloidal behavior of aqueous montmorillonite suspensions: The specific role of pH in the presence of indifferent electrolytes. Applied Clay Sci 27: 75-94.
17. Benna M1, Kbir-Ariguib N, Magnin A, Bergaya F (1999) Effect of pH on rheological properties of purified sodium bentonite suspensions. J Colloid Interface Sci 218: 442-455.
18. Missana T1, Adell A (2000) On the applicability of DLVO theory to the prediction of clay colloids stability. J Colloid Interface Sci 230: 150-156.
19. Polechn HJ, C Liu (2006) Quantitative analysis of montmorillonite platelet size by atomic force microscopy. Ind Eng Chem Res 45: 7025-7034.
20. Luckham PF, Rossi S (1999) The colloidal and rheological properties of bentonite suspensions. Adv. In Colloid and Interf Sci 82: 43-92.
21. Whalley WR, Mullins CE (1991) Effect of saturating cation on tactoid size distribution in bentonite suspensions. Clay Minerals 26: 11-17.
22. Norrish K (1954) The swelling of montmorillonite. Discuss Faraday Soc 18: 120-134.
23. Segad M, Hanski S, Olsson U, Ruokolainen J, Akesson T, et al. (2012) Microstructural and swelling properties of Ca and Na montmorillonite: (In situ) Observations with Cryo-TEM and SAXS. J Phys Chem C 116: 7596-7601.
24. Bailey L1, Lekkerkerker HN, Maitland GC (2015) Smectite clay--inorganic nanoparticle mixed suspensions: phase behaviour and rheology. Soft Matter 11: 222-236.
25. Lagaly G (1989) Principles of flow of kaolin and bentonite dispersions. Applied Clay Science 4: 105-123.
26. Callaghan IC, Ottewill RH (1974) Interparticle forces in montmorilonite gels. Disc Faraday Soc 57: 110-118.
27. Zbik MS, Williams DJ, Song YF, Wang CC (2014) The formation of a structural framework in gelled Wyoming bentonite: Direct observation in aqueous solutions. J Coll Interf Sci 435: 119-127.
28. Ali S, Randyopadhyay R (2015) Evaluation of the exfoliation and stability of Na-montmorillonite in aqeous dispersions. Applied Clay Sci 114: 85-92.
29. Mouzon J, Bhuiyan IU, Hedlund J (2016) The structure of montmorillonite gels revealed by sequential cryo-XHR-SEM imaging. J Colloid Interface Sci 465: 58-66.
30. Au PI, Leong YK (2015) Surface chemistry and rheology of slurries of kaolinite and montmorillonite from different sources. KONA Powder and Particle J 33: 17-32.
31. Barnes HA (1999) The yield stress��?a review or ��?panta roi��?-everything flows? J Non-Newtonian Fluid Mech 81: 133-178.
32. Hartnett JP, Hu RYZ (1989) Technical note: The yield stress-an engineering reality. J Rheol 33: 671-679.
33. Astarita G (1990) Letter to the editor: The engineering reality of the yield stress. J Rheol 34: 275-277.
34. Kelessidis VC, R Maglione, C Tsamantaki, Y Aspirtakis (2006) Optimal determination of rheological parameters for Herschel��?Bulkley drilling fluids and impact on pressure drop, velocity profiles and penetration rates during drilling. J Petr Sci Engr 53: 203-224.
35. Maglione R, Kelessidis VC (2010) Choosing the best rheological model for water-bentonite suspensions. Tech Chron Sci J TCG No 3: 211-226.
36. Vryzas Z, Wubulikasimu Y, Gerogiorgis D, Kelessidis VC (2016) Understanding the temperature effect on the rheology of water-bentonite suspensions, nordic rheology conference (NRC) Helsinki Finland.
37. API Specifications 13A (2010) Specification for drilling fluid materials 18th edition Washington DC
38. API Specifications 13B-1 (2003) Recommended practice for field testing water-based drilling fluids Washington DC.
39. Vryzas Z, Kelessidis VC, Nalbantian L, Zaspalis V, Gerogiorgis DI, et al. (2016) Effect of temperature on the rheological properties of neat aqueous Wyoming sodium bentonite dispersions. App Clay Sci 136: 26-36.
40. Abu-Jdayil B (2011) Rheology of sodium and calcium bentonite-water dispersions: Effect of electrolytes and aging time. Int J Miner Process 98: 208-213.
41. Mahmoud O, Nasr-El-Din HA, Vryzas Z, Kelessidis VC (2016) Nanoparticle-based drilling fluids for minimizing formation damage in HTHP applications, SPE International Conference & Exhibition on Formation Damage Control, Lafayette, Louisiana, USA.
42. Thomas DG (1961) III Laminar-flow properties of flocculated suspensions. AIChE Journal 7: 431-437.
43. Wildemuth CR, Williams MC (1985) A new interpretation of viscosity and yield stress in dense slurries: Coal and other irregular particles. Rheol Acta 24: 75-91.
44. Leong YK, Scales PJ, Healey TW, Boger DV (1995) Effect of particle size on colloidal zirconia rheology at the isoelectric point. J Am Ceram Soc 78: 2209-2212.
45. Zhou Z, Solomon MJ, Scales PJ and Boger DV (1999) The yield stress of concentrated flocculated suspensions of size distributed particles. J Rheol 43: 651-671.
46. Kelessidis VC, Tsamantaki C, Dalamarinis P (2007) Effect of pH and electrolyte on the rheology of aqueous Wyoming bentonite-dispersions. Applied Clay Sci 38: 86-96.
47. Ramos-Tejada MM, Arrovo FJ, Peren R, Duran JDG (2001) Scaling behavior of the rheological parameters of montmorillonite suspensions: Correlation between interparticle interaction and degree of flocculation. J of Colloid and Interf Science 235, 251-259.
48. Laribi S, Fleureau JM, Grossiord JL, Kbir-Ariguib N (2005) Comparative yield stress determination for pure and interstratified smectite clays. Rheol Acta 44: 262-269.
49. Mirnik M (1961) Schulze��?Hardy rule and mass action law. Nature 190: 689-690.
50. Bolto BA (1995) Soluble polymers in water purification. Prog Polym Sci 20: 987-1041.
51. Grini G (2005) Recent developments in polysaccharide-based materials used as adsorbents in wastewater treatment. Prog Polym Sci 30: 38-70.
52. Gray SR, Ritchie CB (2006) Effect of organic polyelectrolyte characteristics on floc strength. Colloids and Surfaces A 273: 184-188.
53. Reid PI, Elliot GP, Minton RC, Chambers BD, Burt DA (1993) Reduced environmental impact and improved drilling performance with water-based muds containing glycols. SPE/EPA Exploration & Production Environmental Conference San Antonio TX.
54. Rossi S, Luckham PF, Zhu S, Briscoe BJ, Tadros TF (1997) Influence of low molecular weight polymers on the rheology of bentonite suspensions. Institute Francais du Petrole 52: 199-206.
55. Rossi S, Luckham PF, Tadros TF (2002) Influence of non-ionic polymers on the rheological behaviour of Na+-montmorillonite clay suspensions-I Nonylphenol-polypropylene oxide-polyethylene oxide copolymers. Colloids and Surfaces A. 201: 85-100.
56. Rossi S, Luckham PF, Tadros TF (2003) Influence of non-ionic polymers on the rheological behaviour of Na+-montmorillonite clay suspensions Part II Homopolymer ethyleneoxide and polypropylene oxide-polyethylene oxide ABA copolymers. Colloids and Surfaces: A Physicochemical and Engineering Aspects 215: 1-10.
57. Young S, T Maas (2001) Novel polymer chemistry increases shale stability AADE 01-NC-HO-41. AADE 2001 National Drilling Conference Drilling Technology-The Next 100 years Houston Texas March.
58. Mongondry P (2003) Structure et comportement rhéologique des suspensions aqueuses de Laponite en présence de plusieurs additifs. Université du Maine - Le Mans French.
59. Benchabane A, Bekkour K (2006) Effects of anionic additives on the rheological behavior of aqueous calcium montmorillonite suspensions. Rheol Acta 45: 425-434.
60. Kelessidis VC, Poulakakis M, Chatzistamou V (2011) Use of Carbopol 980 and Carboxymethyl-Cellulose polymers as rheology modifiers of sodium-bentonite water dispersions. Applied Clay Science 54: 63-69.
61. Abend S, Lagaly G (2000) Sol��?gel transitions of sodium montmorillonite dispersions. Appl Clay Sci 16: 201-227.
62. Duran JDG, Ramos-Tejada MM, Arroyo FJ, Gonzalez-Caballero F (2000) Rheological and electrokinetic properties of sodium montmorillonite suspensions. J Colloidal and Interf Sci 229: 197-117.
63. Permien T, Lagaly G (1994) The rheological and colloidal properties of bentonite suspensions in the presence of organic compounds-III. The effect of alcohols on the coagulation of sodium montmorillonite. Colloid Polym Sci 272: 1306-1312.
64. Kelessidis VC, Tsamantaki C, Pasadakis N, Repouskou E, Hamilaki E (2006) Permeability, porosity and surface characteristics of filter cakes from water-bentonite suspensions. Advances in Fluid Mechanics Conference Skiathos.
65. van Damme H, Levitz P, Fripiat JJ, Alcover JF, Gatineau L, Bergaya F (1985) Physics of finely divided matter in Boccata N, Daoud M (eds), Sprinter-Verlag Berlin 24-30.
66. M��?bodj O, Kbir-Ariguib N, Ayadi MT, Magnin A (2004) Plastic and elastic properties of the systems interstratified clay-water-electrolyte-xanthan. J Colloid Inter Sci 273: 675-684.
67. Pellenq RJ, Lequeux N, van Damme H (2008) Chem Concr Res 38: 159-174.
68. Crocker JC, Grier DG (1998) When like charges attract: The effects of geometrical confinement on long-range colloidal interactions. Phys Rev Lett 77: 1897-1900.
69. Bowen WR, Sharif AO (1998) Long-range electrostatic attraction between like-charge spheres in a charged pore. Nature 393: 663-665.
70. Nikolaides MG, Bausch AR, Hsu MF, Dinsmore AD, Brenner MP, et al. (2002) Electric-field-induced capillary attraction between like-charged particles at liquid interfaces. Nature 420: 299-301.
71. Ise N (2002) When does like like like? Proc Japan Acad Ser B 78: 129-137.
72. Jabbari-Farouji S, Weis JJ, Davidson P, Levitz P, Trizac E (2013) On phase behavior and dynamical signatures of charged colloidal platelets. Scientific Reports 3: 3559.
73. McBride MB, P Baveye (2002) Diffuse double-layer models, long-range forces and ordering in Clay colloids. Soil Sci Soc Am J 66: 1207-1217.
74. Sogami I, Ise N (1984) On the electrostatic interaction in macroionic solutions. J Chem Phys 81: 6320-6332.
75. Onsager L (1949) The effect of shape on the interaction of colloidal like-charged colloidal spheres in electrolyte solutions. Ann NY Acad Sci 51: 627-659.
76. Cadene A, Durand-Vidal S, Turq P, Brendle J (2005) Study of individual Na-montmorillonite particles size, morphology and apparent charge. J Colloid Interface Sci 285: 719-730.
77. Ploehn HJ, Liu C (2006) Quantitative Analysis of Montmorillonite Platelet Size by Atomic Force Microscopy. Ind Eng Chem Res 45: 7025-7034.
78. Frenkel D (2000) Perspective on â�?�?The effect of shape on the interaction of colloidal particlesâ�?. Theor Chem Acc 103: 212-213.
79. Brown ABD, Clarke SM, Rennie AR (1998) Ordered phase of platelike particles in concentrated dispersions. Langmuir 14: 3129-3132.
80. van der Kooij FM1, Kassapidou K, Lekkerkerker HN (2000) Liquid crystal phase transitions in suspensions of polydisperse plate-like particles. Nature 406: 868-871.
81. Gabriel JC, Sanchez C, Davidson P (1996) Observation of nematic liquid-crystal textures in aqueous gels of smectite clays. J Phys Chem 100: 11139-11143.
82. Annis MR (1967) High-temperature flow properties of water-based drilling fluids. J Pet Tech 19: 1074-1080.
83. Alderman JN, Gavignet AA, Guillot D, Maitland CG (1988) High-temperature, high-pressure rheology of water-based muds. Society of Petroleum Engineers Houston Texas.
84. Derjaguin BV, Landau L (1941) Theory of the stability of strongly charged lyophobic sols and adhersion of strongly charged particles in solutions of Electrolytes. Acta Physicochemica URSS 14: 633-652.
85. Verwey EJW, Overbeek, JTG (1948) Theory of stability of lyophobic colloids. Elsevier Amsterdam 216
86. Kapur PC, Scales PJ, Boger DV, Healy TW (1997) Yield stress of suspensions loaded with size distributed particles. AIChE J 43: 1171-1179.
87. Larson RG (1999) The structure and rheology of yield stress fluids. Oxford Univ Press New York.
88. Scales PJ, Johnson SB, Healy TW, Kapur PC (1999) Shear yield stress of partially flocculated colloidal suspensions. AIChE J 44: 538-544.
89. Flatt RJ, Bowen P (2006) Yodel: A yield stress model for suspensions. J Am Ceram Soc 89: 1244-1256.