Simulation and Modelization of Parabolic Solar Concentrator

The Dish Stirling systems have demonstrated the highest efficiency of any solar power generation system by converting nearly 31.25% [1] of direct normal incident solar radiation into electricity after accounting for parasitic power losses. Therefore, the Dish Stirling technology is anticipated to surpass parabolic troughs by producing power at more economical rates and higher efficiencies. Because the Dish Stirling systems are modular; each system is a self-contained power generator, they can be assembled into plants ranging in size from a kilo-watts to 10 MW [2]. These systems can also be combined with natural gas and the resulting hybrid provides continuous power generation like other conventional solar energy systems [3]. Dish Stirling systems are applicable in the regions having high level of Direct Normal Irradiance; the so-called Sun Belt area which includes: the Northern Africa (where Algeria is located), Mexico, Southwest of USA, Australia, MENA region.

The synthesis of theoretical reflections vary thoroughly on the use of the methods of Monte Carlo in radioactive transfers [4]. The scopes of application considered were very vast [5,6].

Stirling dish systems have not been researched as extensively as other solar technologies such as photovoltaic or solar hot water heaters, and literature on these systems is difficult to find and rarely organized in one cohesive report. Data on the performance of Stirling dish systems have typically not been accessible to the public, and few Stirling dish systems have been constructed to date. Despite these limitations, data were obtained from Sandia National Laboratory for the WGA Mod 2-2 Stirling dish system in order to validate models of Stirling dish power systems developed during the course of the present study.

Our software of simulation Greenius is based on the following mathematical model:

The gross electrical performance is given by the equation (1) [7]:

P_gros=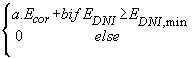

Where E_cor is the corrected irradiance in W/m², EDNI is the direct normal irradiance in W/m² and E_{DNI, min} is the minimal direct normal irradiance for starting generation in W/m².

The coefficients of the gross power are:

a is performance model constant in W_e /(W/m²) and b is the performance model constant in W_e. So the corrected irradiance is given by :E_cor=E_DNI . f_ref . f_temp, and the correction factors are :

f_temp: the temperature correction factor and f_ref: the reflection correction factor.

The expression of the reflection correction factor is given by the equation (2):

f_ref= f_shadowing . f_intercept (2)

Where f_shadowing is the shadowing and blockage factor and f_intercept is the intercept factor.

The temperature correction factor is shown in this equation (3):

F_temp=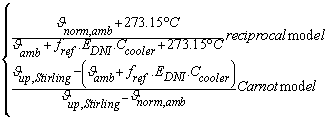

Then ϑ_norm,amb is the normalized temperature for performance model in °c and ϑ_amb is the actual ambient temperature.

or ϑ_up,Stiriling is the upper Stirling temperature in °c and the C_cooler is the cooler constant in °c / (W/m²) .

The data used in this model included the sun elevation angle, cooling water inlet/outlet temperatures, engine pressure, 100 expansion space temperatures (heater head temperature), net power, wind speed, ambient temperature, direct normal isolation, and the average receiver temperature. Plots of key measured data were generated for a clear day (4/26/2009) to better understand the factors influencing the Stirling dish system performance. Two days of data from the summer (7/24/09), and winter (1/13/09) were used to obtain the dish Stirling system used in the Stirling cycle component model. The component model was then compared with experimental data that were not used to establish the efficiency curves. Results of the comparisons are provided for in the “Results Analysis: Comparison of Component Models to Data” section below.

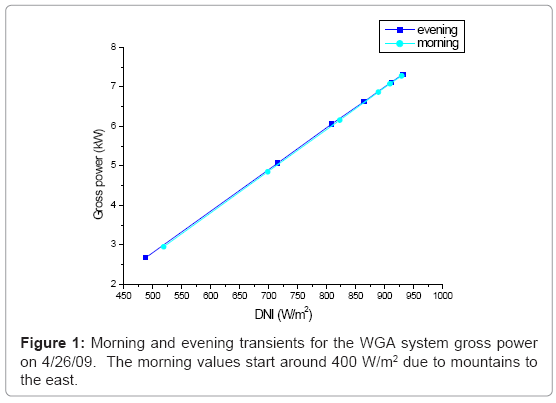
A plot of the gross power versus insolation illustrates the transients in performance during the morning and evening as shown in Figure 1. The Stirling dish systems tend to perform worse in the morning due to the thermal capacitance of the receiver walls and absorber requiring energy to obtain a steady state heater head temperature. Figure 1 also indicates data influenced by shading in the morning resulting from mountains to the east, which eliminates most of the data points at lower insolation values [8]. The effective shading of the mountains results in a curve fit of the data slightly over-predicting the system performance during the morning since the data points recorded at insolation values below approximately 400 W/m² all occur in the evening when the performance is greater. The net effect on the data due to the mountains is expected to be minimal.

Figure 1: Morning and evening transients for the WGA system gross power on 4/26/09. The morning values start around 400 W/m² due to mountains to the east.

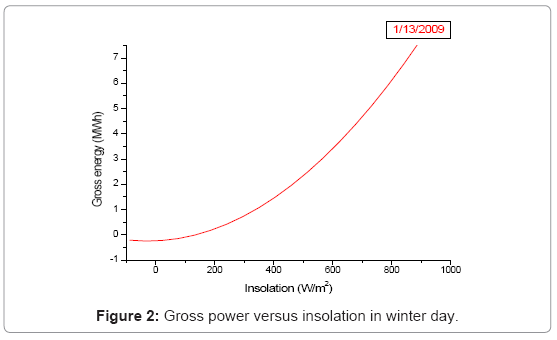
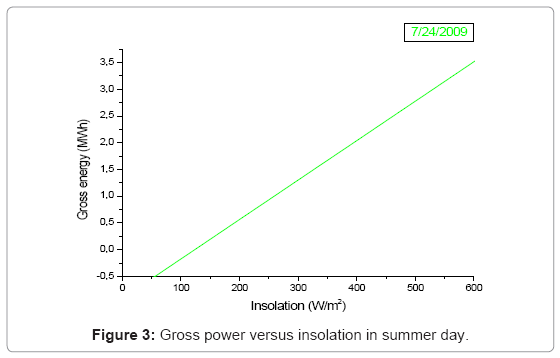
The gross power versus direct normal insolation data were plotted for two days of data in Figures 2 and 3. The figure shows lower performance during start-up during colder temperatures, but this could also be affected by the location the sun rises over the eastern mountains during different times of the year. The data does indicate higher performance once the system has been running at lower ambient temperatures.

Figure 2: Gross power versus insolation in winter day.

Figure 3: Gross power versus insolation in summer day.

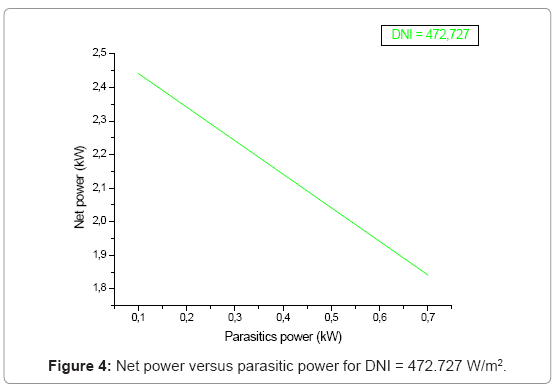
At lower ambient temperatures, the receiver losses are also greater, so the net power versus direct normal insolation will not be as high at colder temperatures in comparison to the efficiency curves.

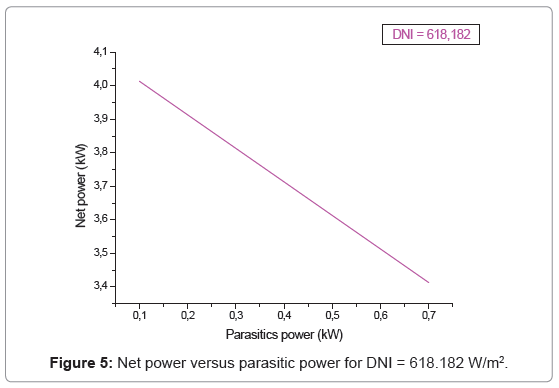
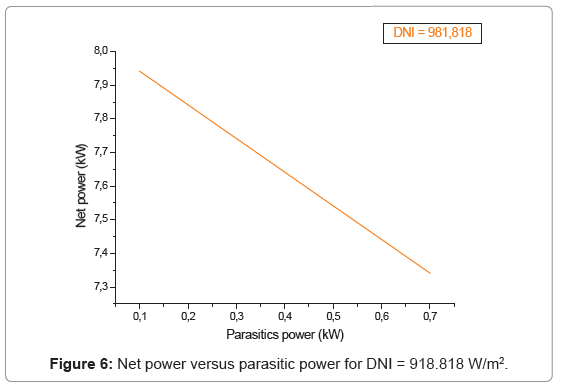
Large parasitic power loads resulted in large negative values for the net power. The data included the net power (Figures 4-6 at different isolations), but not the gross power, so data with negative net power values were filtered out in order to obtain better values for the performance prediction simulations. The parasitic power can become greater than 1.0 kW early in the morning or evening due to starting the engine and the collector leaving or entering the stow position. The additional large parasitic power loads throughout the day most likely resulted from system faults or cloud conditions requiring the engine to shutdown and restart. These data were filtered.

Figure 4: Net power versus parasitic power for DNI=472.727 W/m².

Figure 5: Net power versus parasitic power for DNI = 618.182 W/m².

Figure 6: Net power versus parasitic power for DNI = 918.818 W/m².

A computational model was created and used to investigate the effects of system design parameters for a Stirling dish system. The model, implemented in Greenius, can be used to predict the variation of the net energy production in a specific location using input weather data files. The model is expected to have greater accuracy predicting the system performance in different locations due to the additional properties of the wind velocity, sun elevation angle, and altitude. This model ideally will be used by designers to optimize design parameters and by researchers or utilities to obtain a better representation of a Stirling dish systems location specific performance.