Research Article Open Access
Impacts of Multi Resolution Species Distributional Information Analyzing Macroecological Patterns
Youhua Chen*Department of Zoology, University of British Columbia, Vancouver, Canada
- *Corresponding Author:
- Youhua Chen
Department of Zoology
University of British Columbia
Vancouver, Canada
E-mail: yhchen@zoology.ubc.ca
Received date: July 01, 2013; Accepted date: September 25, 2013; Published date: September 27, 2013
Citation: Chen Y (2013) Impacts of Multi Resolution Species Distributional Information Analyzing Macroecological Patterns. J Ecosys Ecograph 3:137. doi:10.4172/2157-7625.1000137
Copyright: © 2013 Chen Y, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and and source are credited.
Visit for more related articles at Journal of Ecosystem & Ecography
Abstract
In this brief report, a simple scaling algorithm was developed for reconstructing range cells upon the original pixellevel distributional points of species. The algorithm could generate the distributional cells of species that covers all the original distributional points of species, but being with varying spatial resolutions (i.e., different sizes of the smallest operative area unit). As such, I could quantitatively evaluate the macroecological patterns (including richness, rarity hotspots, and the influence of spatial autocorrelation on structuring species’ richness and rarity patterns) on the basis of these varying-resolution species distributional layers. Resultant diversity patterns thus could be compared to the true patterns directly derived from species’ original distributional points. The present theoretical results showed that, the macroecological patterns identified from varying-resolution data could be basically consistent to those from the true distributional data, as long as there were not many multi-scaling distributional layers inside the whole dataset. However, the estimated macroecological patterns would be far departed from the true ones when there were a remarkable number of multi-scaling layers inside. Thus, I argued that the varying-resolution data could be utilized but with some cautions so as to accurately reveal ecological patterns and interpret the relationship between species diversity, distribution and environment.
Keywords
Range maps; Distribution of species; Environment- Range size relationship
Introduction
In macroecological studies, researchers require to utilize a great number of landscape digitized maps of objects. For example, distributional ranges of species [1-3], the zonation of different biogeographic regions and ecoregions [4,5], NDVI vegetation index [6,7] and so on. However, a potential problem when combining these digitized maps together for performing subsequent analysis is that they are typically produced from different spatial resolutions, which may lead to the misinterpretation of the macroecological patterns [2,8].
Although the mixed-resolution problem of spatial landscape maps is not hard to image and may be a common sense to some extent, there is not a systematic and quantitative assessment of the impacts of utilizing varying-scaling digitized maps on influencing spatial patterns of focusing objects (e.g., species distribution, for which I will discuss hereafter) in previous literature. Thus, it would be worthy to perform a holistic assessment of the multi-scaling issue when one utilizes digitized maps from different sources and with various spatial resolutions.
In the present study, a simple algorithm was developed for reconstructing varying-resolution distributional cells of species distribution on the basis of original distributional points. The scaling algorithm could generate multi-resolution species distribution data, which could be used to infer macroecological patterns and compared to those from true distributional points.
The central purpose of the present report is to evaluate the impacts of mixing multi-resolution distributional data of species into the whole data set on influencing macroecological patterns. I will investigate how the degree of difference between the true and estimated macroecological patterns is. Without further clarification, the true macroecological patterns refer to the patterns constructed from the original distributional points of species at pixel spatial level (the highest resolution). By contrast, the estimated macroecological patterns refer to those constructed from the distributional cells of species at various spatial resolutions.
Materials and Methods
Generation of distribution points using Poisson cluster process
The distribution of species across the boundary was generated using Poisson cluster process, following the method illustrated in the previous work [9]. In brief, I created a random number of parental points for a species using a Poisson process with intensity ρ . Then, each parental point produces a random number of offspring points, drawn independently from one of any probability models. Here, I considered the offspring numbers were drawn from a geometric distribution with parameter 0.01.
The positions of offspring points relative to their parental point are drawn randomly from a bivariate probability density function 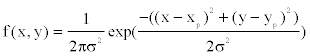 where
where 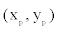 denotes the location of the parental point in the study grid cells. σ2 controls the dispersion parameter of the data points. After generating all offspring points for the species, the parental points are erased to form the distribution points of the species across the boundary. I simulate 100 species and their distribution points in a grid-cell system with cell sizes 200× 200 . The distribution points of each species thus were analyzed to obtain the range cells of the species with a new spatial resolution using the scaling method introduced below.
denotes the location of the parental point in the study grid cells. σ2 controls the dispersion parameter of the data points. After generating all offspring points for the species, the parental points are erased to form the distribution points of the species across the boundary. I simulate 100 species and their distribution points in a grid-cell system with cell sizes 200× 200 . The distribution points of each species thus were analyzed to obtain the range cells of the species with a new spatial resolution using the scaling method introduced below.
Construction of varying-resolution distributional cells of species using original distributional points
Imaging that a sampling area is composed of pixel points (since I have a grid-cell system with200× 200 , thus the total pixel number=40000) and some pixel points were marked by 1 when the species’ original distributional points were congruent with these points. In contrast, other pixel points were marked by 0, indicating that the absence of species. This map showed the original distributional points of species, having the highest spatial resolution (pixel level).
The scaling algorithm assigned the equal spatial cell units into the sampling area. The size of the cell unit is determined by the resolution (should be an integer). These units jointly cover the all the area and no overlapping of different units is allowed. As such, all the pixel points bounded by a cell were marked with 1 as long as at least one distributional point of species was found inside that cell. In contrast, if no distributional points were found inside, all the pixel points inside the cell were marked by 0, indicating absence of the species. If the cell covers the edge of the sampling area (thereby some part of the cell may situate out of the area), I only consider the part inside the whole area.
By this means, after checking all the cells across the whole area, all the cells and their accompanying pixel points (all marked with 1 if species is present, 0 if absent) were stored as a new distributional layer, showing the distributional pattern of the species at a new given resolution (indicated by the spatial unit). This new distributional map for the species with a new spatial resolution (in comparison to the original map at pixel spatial level) is generated and mixed into the original data set to generate a multi-resolution data set.
For different species, different resolution parameters were randomly drawn (following a certain probability density function) to generate varying-resolution distributional maps of species. These multi-resolution maps were then utilized to generate macroecological patterns. As a comparison, the macroecological patterns straightforwardly derived from original pixel-level distributional points of the species were analyzed as well, which were quantified as the true macroecological patterns to check the disparity of patterns inferred from multi-scaling distributional maps.
I used a Poisson distribution to generate the resolution parameter for different species. Thus, for each species, the reconstructed distributional map having the resolution being equal to Poisson( λ ) +1. If resolution>100, the distributional map is identical to the original pixellevel distributional map. Otherwise, when the resolution≤ 100, the new map is a coarse-size representation of species’ original distribution. For example, when the resolution=100, the coarse-size map will have 100 × 100 pixels. Because each resolution value is randomly drawn from the Poisson probability, thus I could readily obtain mixing multi-resolution distributional layers in the whole data set, in which some will have the original pixel-level distribution without scaling, while others have coarse-resolution distribution after scaling. I set the mean parameter λ =100, 80, 60, and 40 respectively to perform the comparison of different degrees of multi-scaling patterns and their impacts on reconstructed macroecological patterns.
Analysis of macroecological patterns
I measured the following macroecological patterns, including the species richness hotspots and rarity hotspots [10-12]. These features are widely studied across different spatial resolutions so as to figure out the key areas as conservation priorities [13]. They are also employed to reveal the environment-diversity patterns [14].
I further analyzed spatial autocorrelation patterns using the true distributional points and the varying-resolution distributional cells. I evaluated the impact of spatial autocorrelation on structuring richness and rarity hotspots of species using an autoregressive model [15-17].
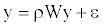 (1)
(1)
Where W is the row-standardized weighting matrix, ρ is the autoregressive parameter (we set 0 ≤ ρ ≤1) and ε is the error vector. This model was fitted by maximum likelihood procedures. Squared correlation between the observed richness ranking y and the estimated 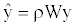 gives the pseudo- R2 of the model, showing the proportion of explained variance attributed to the spatial autoregressive process.
gives the pseudo- R2 of the model, showing the proportion of explained variance attributed to the spatial autoregressive process.
There are lots of possible weighting matrices W, the simple one is the matrix identical to the one defined in Moran’s I formula as,
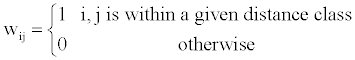 (2)
(2)
A preliminary analysis showed that the distance class is set to 2 could give a moderately high pseudo- R2 and low AIC values. As such, the W matrix is derived from the distance class 2 across different scenarios.
A comparison of macroecological patterns
For performing the comparison of macroecological patterns generated using varying-resolution maps and true distributional pixel points of species, I considered the Pearson’s correlation test [18] to compare the results generated from range cells and original points.
Results
A comparison of richness and rarity hotspots
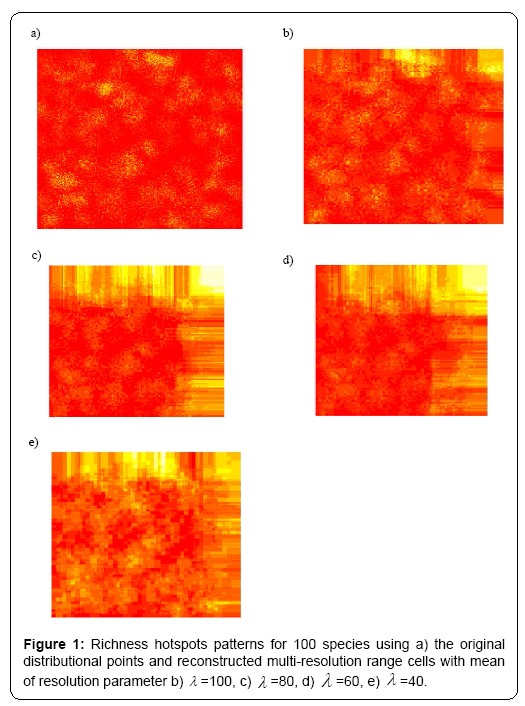
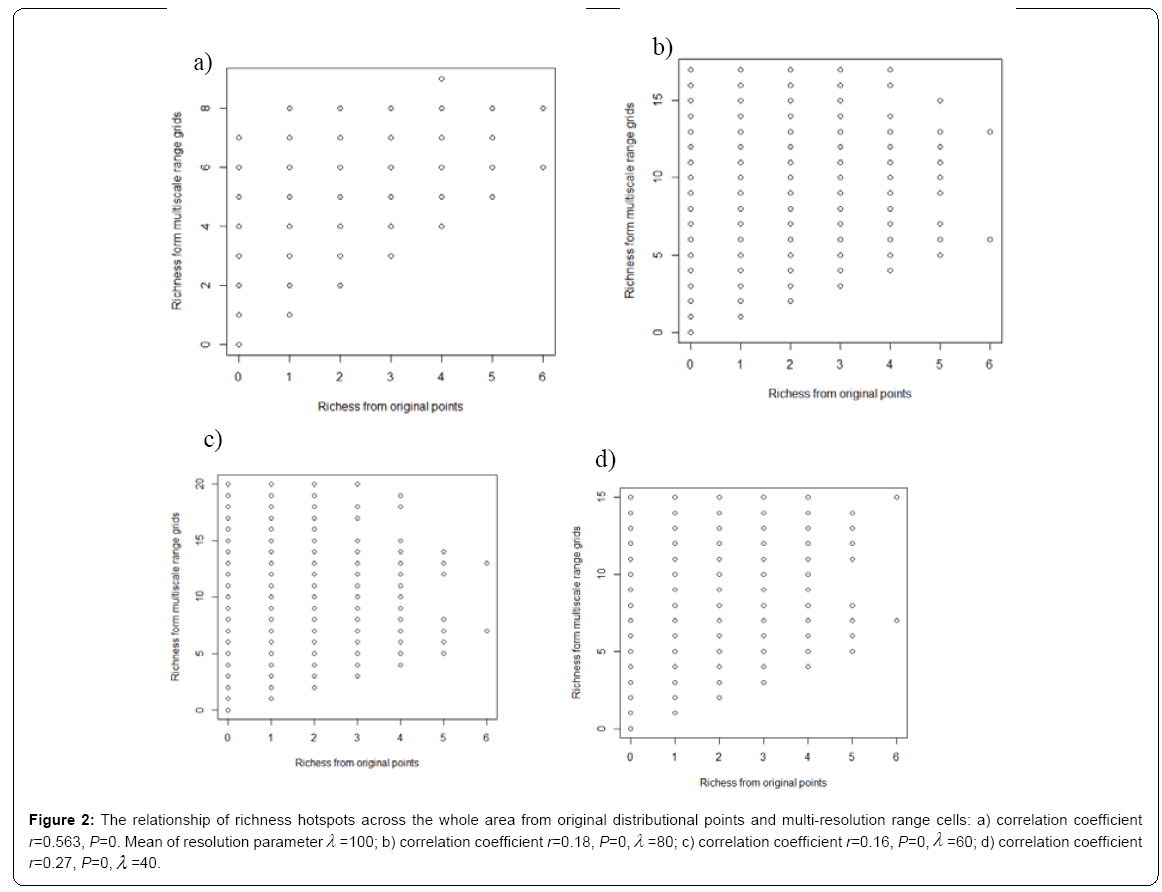
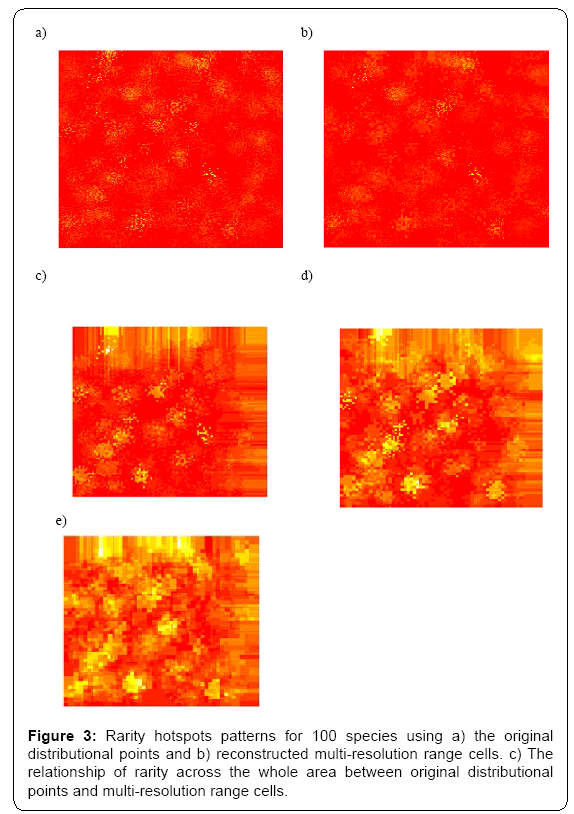
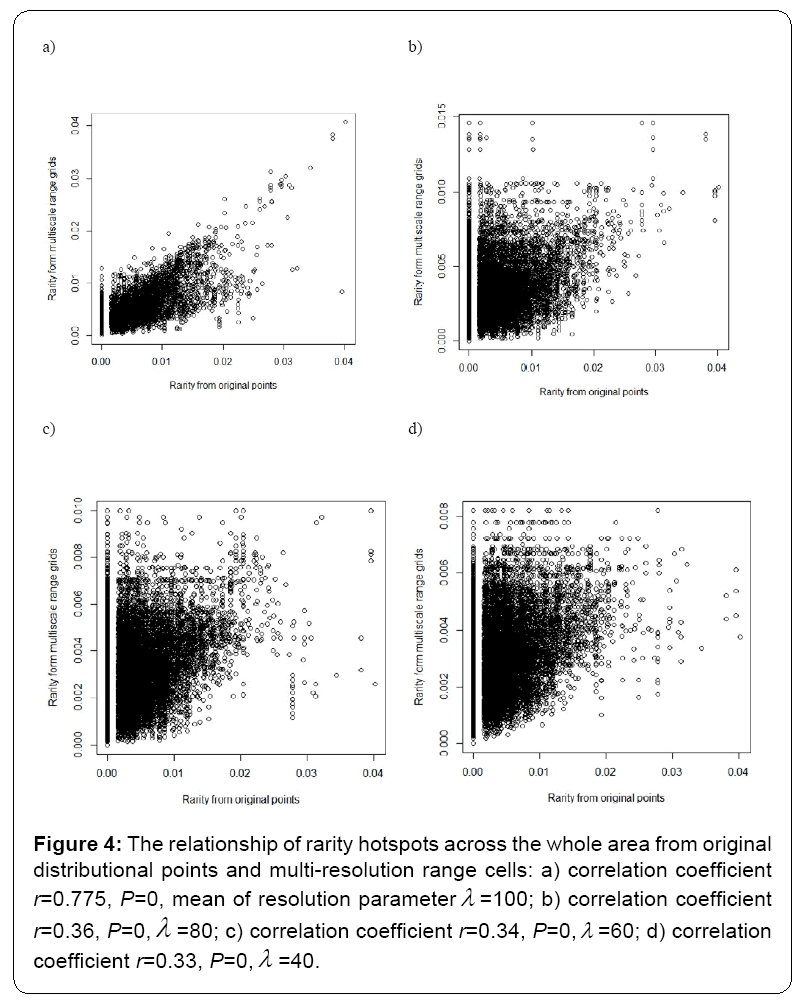
Under different multi-resolution scenarios, it is observed that the hotspots patterns could be basically congruent among different multiresolution distribution of species. As showed in the correlation values presented in the legend of Figure 2, there is a nonlinear relationship between mean resolution parameter λ and correlation coefficient r on richness hotspots patterns. Increasing resolution parameter λ could not always result into the reducing correlation r, contradictory to my initial prediction. However, for rarity hotspots patterns, I did observe that increasing resolution parameter λ could result into the reducing correlation coefficient r (as showed in the correlation values presented in the legend of Figure 4).
A comparison on the role of spatial autocorrelation on influencing species richness and rarity
Under different multi-resolution scenarios, it is found that the influence of spatial autocorrelation varied accordingly (Table 1). For the cases that species’ distributions have low mean resolution parameter λ (meaning the resolution is low), the influence of spatial autocorrelation was stronger for either rarity or richness patterns (indicated by the explained variance R2 in the autoregression model). However, when the distributions of species have the higher chance of keeping their original pixel distributional points (i.e., higher λ ), the influence of spatial autocorrelation was reduced in general. Furthermore, the resolution parameter λ has a nonlinear relationship with the autoregression model coefficient ρ (Table 1).
| Richness | Rarity | |||||
|---|---|---|---|---|---|---|
| Data | ρ | AIC | R2 | ρ | AIC | R2 |
| Original | 0.001524 | 21334.3 | 0.572595 | 0.00171 | -12330.4 | 0.567422 |
| λ =100 | 0.001814 | 23625.66 | 0.61562 | 0.001631 | -13953.2 | 0.501253 |
| λ =80 | 0.003846 | 27587.93 | 0.854435 | 0.002493 | -17104.8 | 0.738656 |
| λ =60 | 0.003015 | 28533.39 | 0.80411 | 0.002448 | -17140.4 | 0.727141 |
| λ =40 | 0.002071 | 28386.11 | 0.699919 | 0.00205 | -17098.2 | 0.692105 |
Table 1: Influence of spatial autocorrelation on species’ spatial richness and rarity patterns derived from varying-scaling distribution information of 100 species.
Overall, the explained variance R2 for different kinds of multiscaling datasets is always larger than 0.5, indicating that spatial autocorrelation played an essential role in structuring species richness and rarity patterns.
Discussion
As showed in the results, I found that there were basically emerging disparities between the true and estimated macroecological patterns. When there are still a lot of distributional maps of species kept in original pixel-resolution level in the whole data set, the discordance between the true and estimated patterns is minor. As such, my study showed that for keeping the results being consistent, the multi-scaling data sets must be transformed and rescaled so as to keep in line with their resolutions. By this means, the resultant analysis of macroecological patterns could be more reliable and stable without changing a lot.
When the average resolution λ of the data becomes lower, the resultant macroecological patterns showed inflated patterns, indicating that the variation of the data is reduced greatly. As such, I found that the signals of spatial autocorrelation are much stronger (Table 1). In contrast, the variation of the data is only able to be reflected by using low-resolution or pixel-level landscape maps. As showed in Table 1, the variation of the data becomes highest at the pixel-level of the data (consequently the explained variance R2 was lowest for the pixel-level distributional data). Conclusively, choosing the small spatial-resolution data (high λ ) for ecological studies seemed much better than those large spatial-resolution data (low λ ), if one only tries to capture and analyze the variation of the landscape data as much as possible.
As the implications, it would be valuable to further assess the impacts of multi-scaled data on inferring the relationships of species distribution, environment and space. Thus, it is required that one could construct species distributional patterns under the constraint of environmental gradients. As such, the Poisson cluster model used in my study should be modified to accommodate the influence of environmental forces. Constrained distribution of species under environmental and spatial limitations would offer new theoretical insights into the environment-diversity relationships. Also, it could help us better quantify how the interaction of niche (i.e., environment) and neutrality (i.e., space) could result in different patterns of species distribution.
In summary, the present study offered some information on the impacts of varying-resolution spatial layers influencing macroecological patterns. Basically, when there are not many multi-scaling species distributional layers inside the whole dataset, the resultant richness and hotspots patterns were basically consistent with those from the original true distributional points (high resolution parameter λ ). However, when there is an increasing number of multi-scaling distributional layers (low λ ) for the analysis, there will be an increasing disparity of the macroecological patterns for the multi-scaling and true data: the correlation between the true and estimated patterns will be much lower (Figures 1-4), and the influence of spatial autocorrelation will be much higher (Table 1: R2 ).
Figure 2: The relationship of richness hotspots across the whole area from original distributional points and multi-resolution range cells: a) correlation coefficient r=0.563, P=0. Mean of resolution parameterλ =100; b) correlation coefficient r=0.18, P=0,λ =80; c) correlation coefficient r=0.16, P=0,λ =60; d) correlation coefficient r=0.27, P=0,λ =40.
Figure 4: The relationship of rarity hotspots across the whole area from original distributional points and multi-resolution range cells: a) correlation coefficient r=0.775, P=0, mean of resolution parameterλ =100; b) correlation coefficient r=0.36, P=0,λ =80; c) correlation coefficient r=0.34, P=0,λ =60; d) correlation coefficient r=0.33, P=0,λ =40.
References
- Tittensor DP, Mora C, Jetz W, Lotze HK, Ricard D, et al. (2010) Global patterns and predictors of marine biodiversity across taxa. Nature 466: 1098-1011.
- Hurlbert AH, Jetz W (2007) Species richness, hotspots, and the scale dependence of range maps in ecology and conservation. PNAS 104: 13384-13389.
- Kier G, Kreft H, Lee TM, Jetz W, Ibisch P, et al. (2009) A global assessment of endemism and species richness across island and mainland regions. PNAS 106: 9322-9327.
- Jetz W, Fine PVA (2012) Global gradients in vertebrate diversity predicted by historical area-productivity dynamics and contemporary environment. PLoS Biol 10.
- Chen Y, Bi J (2007) Biogeography and hotspots of amphibian species of China: Implications to reserve selection and conservation. Curr Sci 92: 480-489.
- Pau S, Gillespie TW, Wolkovich EM (2012) Dissecting NDVI-species richness relationships in Hawaiian dry forests. J Biogeogr 39: 1678-1686.
- Gillespie TW, Foody GM, Rocchini D, Giorgi AP, Saatchi S (2008) Measuring and modelling biodiversity from space. Prog Phys Geog 32: 203-221.
- Hurlbert AH, White EP (2005) Disparity between range map and survey based analyses of species richness: patterns, processes and implications. Ecol Lett 8: 319-327.
- Plotkin JB, Potts MD, Leslie N, Manokaran N, Lafrankie J, et al. (2000) Species-area curves, Spatial aggregation, and Habitat specialization in tropical forests. J Theor Biol 207: 81-99.
- Williams P, Gibbons D, Margules C, Rebelo A, Humphries C, Pressey R et al (1996) A comparison of richness hotspots, rarity hotspots, and complementary areas for conserving diversity of British birds. Conserv Biol 10: 155-174.
- Williams PH (1996) Mapping variations in the Strength and Breadth of Biogeographic transition zones using species turnover. Biol Sci 263: 579-588.
- Chen YH (2007) Prioritizing avian conservation areas in China by hotspot scoring, heuristics and optimisation. Acta Ornithologica 42: 119-128.
- Myers N, Mittermeier RA, Mittermeier CG, Da Fonseca GAB, Kent J (2000) Biodiversity hotspots for conservation priorities. Nature 403: 853-858.
- Qian H (2010) Environment-richness relationships for mammals, birds, reptiles and amphibians at global and regional scales. Ecol Res 25: 629-637.
- Vieira C, Blmires D, Diniz-Fiho J, Bini L, Rangel T (2008) Autoregressive modelling of species richness in the Brazilian Cerrado. Braz J Biol 68: 233-240.
- Diniz-Filho JAF, Ramos De Sant’Ana CE, Bini LM (1998) An eigenvector method for estimating phylogenetic inertia. Evolution 52: 1247-1262.
- Diniz-Filho JAF, Cianciaruso MV, Rangel TF, Bini LM (2011) Eigenvector estimation of phylogenetic and functional diversity. Functl Ecol 25: 735-744.
- Rodgers JL, Nicewander WA (1988) Thirteen ways to look at the correlation coefficient. The American Statistician 42: 59-66.
Relevant Topics
- Aquatic Ecosystems
- Biodiversity
- Conservation Biology
- Coral Reef Ecology
- Distribution Aggregation
- Ecology and Migration of Animal
- Ecosystem Service
- Ecosystem-Level Measuring
- Endangered Species
- Environmental Tourism
- Forest Biome
- Lake Circulation
- Leaf Morphology
- Marine Conservation
- Marine Ecosystems
- Phytoplankton Abundance
- Population Dyanamics
- Semiarid Ecosystem Soil Properties
- Spatial Distribution
- Species Composition
- Species Rarity
- Sustainability Dynamics
- Sustainable Forest Management
- Tropical Aquaculture
- Tropical Ecosystems
Recommended Journals
Article Tools
Article Usage
- Total views: 14157
- [From(publication date):
December-2013 - Dec 17, 2025] - Breakdown by view type
- HTML page views : 9507
- PDF downloads : 4650