Independent Prognostic Factors: When is Enough Enough?

The identification of prognostic factors is of prime pursuit in the world of oncology and oncologic research. Although a fairly intuitive concept, one might define a prognostic factor is a patient parameter from which can be gleaned an expected deviation in a given measurable outcome, usually survival or response to some sort of intervention. The “independent” nature of a given prognostic factor is established by multivariate statistical analysis delineating its independence from other prognostic factors [1]. Independent prognostic factors can be particularly useful in clinical medicine since, by their independence, they can be applied to various clinical scenarios and they can be relied upon even in the absence of other clinical information. As a consequence, the identification of independent prognostic factors is a major focus of oncologic study, one that will likely continue ad infinitum. But, as the common aphorism compels us to ask, when is enough enough?

A review of the epidemiologic literature fails to highlight whether there exists an optimal number of independent prognostic factors. This pursuit would be wise for those interested in cost efficiencies, however. In an ideal world, clinical information would be league and cheap; in reality, however, the extraction of relevant clinical data can be arduous and expensive. Many independent prognostic factors, furthermore, have an associated laboratory price tag which, if genomics are considered for example, can be considerable.

The most robust and foolproof approach along the above lines would be to perform a well-designed combinatorial study of a reasonably large sample of patients with well-defined independent prognostic data available to determine if an optimum of independent prognostic factors exists (and, if so, how many). This might be possible with sufficient financial and logistical support. I would suggest, however, first considering the problem from a theoretical perspective, using few basic mathematical arguments, as outlined below.

A thought experiment

Imagine an omniscient clinician capable of at once delimiting all the possible independent prognostic factors pertinent to a given patient. We could easily assume these to be infinite in number (though certainly countable); indeed, this would be of little mind to an omniscient clinician. If our clinician were truly omniscient, (s)he would also be able to rank his/her independent prognostic factors in order from greatest to least impact, with each attributed to its own effect on the patient’s survival, both adding to and subtracting from it.

Thus for each positive independent prognostic factor xi, we have an associated increment in the patient’s expected survival 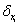where by 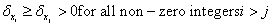.Likewise, for each negative independent prognostic factor y_i, we have an associated decrement in the patient’s expected survival .

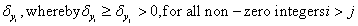Our clinician could then sum these increments and decrements to give an overall expected survival:

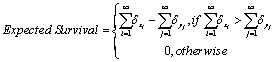
Noting that the sum of increments and decrements cannot amount to a non-zero expected survival. Our clinician would also know that, were the patient free of disease (and hence not a patient of his/hers), (s)he might be expected to live c years (ignoring, for our purposes, the variability in life expectancy that comes with increasing age, gender, heredity and location in the world). This then imposes a ceiling on any calculation of expected survival, since with any disease we cannot reasonably expect to live longer than without. Hence:

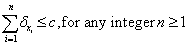
Likewise, the negative prognostic factors could never take away more life lived than could be expected without disease. Hence:

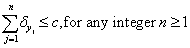
Considering that our clinician is omniscient, (s)he might as well calculate each specific value; but since (s)he has no time (between running clinics, doing research, cooking dinner and putting the kids to bed), our clinician would prefer to model the above sums by a continuous function and thereby estimate what the sum of these independent prognostic factors might look like. In particular, focusing our attention on only the positive independent prognostic factors (since the equations for both positive and negative independent prognostic factors look pretty much the same), our clinician decides to highlight the following:

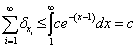
Now we can switch our focus to a more easily characterized continuous function:

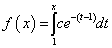
Unfortunately, as our omniscient clinician knows, the above function has no specific optimum except at its point of origin. But considering that our clinician is cunning, (s) he considers the specific case in which:

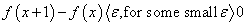
since, beyond this point x, the function f will not change significantly. Now, evaluating:

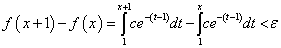
And solving for x, we have:

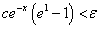
Or,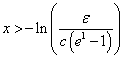

In other words, more than 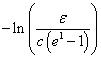each of ranked positive and negative independent prognostic factors is unlikely to contribute significantly to expected survival.

Now our clinician can substitute some specific numbers. For example, consider a baby born today to a rich family in Sweden with no heritable diseases. This baby might be expected to live for, say, c=80 years (or approximately 29200 days). Now suppose some horrible cancer befalls this baby immediately after birth and our clinician wants to know how many x ranked independent positive and y ranked independent negative prognostic factors (s)he should consider when evaluating this baby such that a difference of, for example, 1 day of expected survival could be discerned (i.e. we let 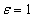).By the above equation we need

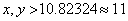
So, in our hypothetical scenario, more than 11 positive and 11 negative ranked independent prognostic factors will add little additional information.

Should we stop at 22 independent prognostic factors if we have more at our disposal? Probably not… Nevertheless, the above thought experiment raises some interesting points pertaining to the discussion that has yet to be had in accounting for the value (or lack thereof) that ever increasing numbers of independent prognostic factors might have.

The availability of modern vast patient registry datasets could allow us a great opportunity to evaluate heretofore-defined prognostic factors over large populations. To these datasets we could apply our knowledge of independent prognostic factors, in concert with known outcome data, to see what combinatorial arrangement of variable numbers of specific prognostic factors produces an optimum of predictive power. I hope that the above might stand as an epidemiologic call-to-arms; such an undertaking would undoubtedly be welcomed by the many nonomniscient clinicians of the world.