A Biomechanics Analysis of Diagnosing Chronic Lumbago
Received: 12-Aug-2025 / Manuscript No. DPO-25-169741 / Editor assigned: 14-Aug-2025 / PreQC No. DPO-25-169741 / Reviewed: 18-Aug-2025 / QC No. DPO-25-169741 / Revised: 25-Aug-2025 / Manuscript No. DPO-25-169741 / Accepted Date: 01-Sep-2025 / Published Date: 01-Sep-2025 QI No. / DPO-25-169741
Abstract
Lower back pain frequently occurs in modern humans for complex reasons. Some aspects of the mechanism are still not fully understood. The primary aim of this research is to analyze the causes of swelling, inflammation and pain in the psoas muscles resulting from intervertebral disc degeneration (L3-L4) using the biomechanical theorem of hoop stress. The secondary aim is to convert these stress data into a pain index using granular computing. We organized and analyzed the psoas muscle stress (hoop stress) across different genders, weights, bending postures and age groups. The pain factors are divided into 10 levels. Each patient's pain factor and condition are assessed after a medical examination. A total of 1400 patients are included in this research. The results show that up to 20 times the body weight acts on the psoas muscles during lumbar flexion. It also indicates that the pain factor (hoop stress) at the L4-L5 intervertebral disc is about 1.3 times larger than at L3-L4 for both males and females.
Keywords: Psoas muscles, Hoop stress, Intervertebral disc degeneration, Granular computing, Pain factor
Introduction
Clinical studies indicate that lower back pain is caused by fatigue and aseptic inflammation of the psoas muscles [1-14]. Longitudinal stress which can be approximated by the concept of hoop stress is a major factor [15]. During lumbar flexion, the psoas muscles bend into an annular form, inducing longitudinal stress. Cyclic motion causes the accumulation of longitudinal stress, leading to psoas muscle fatigue and swelling inflammation. This research calculates longitudinal stress under different conditions, such as body weight, lumbar flexion angle and weight of the lifting object, using biomechanical analysis. The L4 vertebra is subjected to pressure from L3 and L5, along with the lumbar facet joints, ligaments and surrounding soft tissues. For simplification, this research focuses on major portions (L3, L5, lumbar facet joints) in the 3D model. Shear force on the intervertebral disc is calculated using stress transformation for different body weights, lumbar flexion angles and object weights, providing valuable information on stress distribution in the L3-L4 and L4-L5 structures. Granular computing offers a structured, multi-level understanding of the problem. This research adopts a bottom-up approach to pain factor calculation, integrating multiple perspectives such as gender, age, weight, hoop stress and pain factors [16,17].
Materials and Methods
Biomechanical analysis
Human Factor Engineering plays a crucial role in practical applications. As shown in Figure 1, a mechanics analysis of a person with lumbar flexion to pick up an object, where W is the weight of the object, Wa is the weight of the arms, Wt is the weight of the torso (head, neck), Fm is the tension of the psoas muscles to maintain body balance. According to Newton’s First Law, the sum of the moments on an equivalent body should be zero. Therefore, summing the moments at the black spot, we have:

Where Dt, Da, Dw, Dm are the distance from the torso, arms, center of the object and the psoas muscles to L4, respectively. The force acting at L4 as in Figure 2 will be the summation of Fm and all the weights in the direction.

Where is the angle of lumbar flexion. After the force FC acting on the intervertebral disc between L3 and L4, we can easily get the shear force Fs:

According to Figure 3, the psoas major is the primary muscle under stress when bending forward and its upper attachment points are located on the lumbar vertebrae from L1 to L5. As a result, the circumferential stress amplifies the original stress condition.
Longitudinal stress (σi) is then induced in the psoas muscles which can be approximated by using the concept of Hoop stress (σP).
The longitudinal stress of the psoas muscles is a stress due to the internal pressure of the circular inner wall. It is derived according to Newton’s First Law. The unit is or pascals.
The formula for longitudinal stress is:

Where is the longitudinal stress,
p is the pressure to push the intervertebral disc out,
θ is the angle of FC and the intervertebral disc,
d is the inner diameter of the ring,
t is the thickness of psoas muscles.
Actually, there is a thin wall constraint for hoop stress. Using the data above, we can easily get the inner radius of the ring. Plugging in the data, we have:

The longitudinal stress is easily calculated from the equation above. This pressure acts when the disc protrudes, causing abnormal stretching and then swelling and inflammation of the muscle. So far, we have considered only the stress from L3 to L4. Figure 4 is a 3D diagram for stress analysis in L4. Stress from L5 will also be analyzed.
As shown in Figure 4, the blue area is the L4 vertebra. The origin of the xyz coordinates is located at the centroid of the upper surface mass center of the body. And are the pressure from L3 and L5 and θ up and θ down are the angles between each pressure with z axis. It is worth mentioning that these two joints can rotate freely due to the balland- socket joint assumption; there are no reaction moments at these two joints, i.e., M1x=M1y=M1z=M2x=M2y=M2z=0. We only have six reactions (R1x, R1y, R1z, R2x, R2y and R2z). However, R1x=R2x, R1y=R2y, R1z=R2z under normal condition. There is no component in y-direction of FC mentioned before, so we have. R1y=R2y=0. We have only three unknowns (R1x and R1z) and therefore we can easily get the unknowns based on the three equilibrium equation of force in xyz directions. The results are more realistic if we consider the contribution of in x-direction when calculating hoop stress.
Pain factor computing
Grouping: Using granular computing, the main Group (G) is divided into subgroups by gender and age, resulting in 14 sub-groups: GM2-GM8 for males and GF2-GF8 for females, each with 100 samples as in Figure 5.
Data base setup : Millions of medical imaging records are stored in the hospital PACS system as DICOM files. We selected PACS data from May 2018 to April 2021 as the source of this research. The mentioned 14 sub-groups are sampled by age, satisfied by random sampling. Those with an even number at the end of the image check number were selected. Each sub-group draws 100 cases in order of time, establishing a data base of 1400 cases in total.
Data modeling: Fourteen gender sub-group document files were created by inputting data into an Excel program manually as the unit of calculation as shown in Table 1. Each data point in each Excel file must be substituted into the hoop stress formula mentioned above to get the hoop stress of the psoas major. According to the formula, the hoop stress of the psoas major can reach up to 20 times the body weight of a person when the lumbar flexion angle is 15°. Therefore, we use every double as a PF stratification boundary. That is, hoop stress less than 2 times body weight is the first layer (Pain Factor (PF) is 1). The ratio of hoop stress to body weight from 2 to 3.9 is the second layer (PF is 2) and so on, up to 10 levels. In this way, the hoop stress of the psoas major muscle of each sub-group can be mapped to PF and the predicted intensity of pain can be quantitatively evaluated. The correspondence between PF and clinical symptoms is shown in Table 2. Finally, we use equations (5) and (6), statistical formulas [18], to calculate the mean value and standard deviation (s) of each sub-group, then obtain the distribution of the PF level vs. age and gender.

| Age group | Sub-group (gender) | Sub-group (PF) | ||
|---|---|---|---|---|
| GM | GF | GM PF | GF PF | |
| 81-90 | GM8 | GF8 | GM8PF | GF8PF |
| 71-80 | GM7 | GF7 | GM7PF | GF7PF |
| 61-70 | GM6 | GF6 | GM6PF | GF6PF |
| 51-60 | GM5 | GF5 | GM5PF | GF5PF |
| 41-50 | GM4 | GF4 | GM4PF | GF4PF |
| 31-40 | GM3 | GF3 | GM3PF | GF3PF |
| 21-30 | GM2 | GF2 | GM2PF | GF2PF |
Table 1: Sub-groups with PF index.
| PF Level | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Ratio of hoop stress to body weight | <2 | (2,4) | (4-6) | (6-8) | (8-10) | (10-12) | (12-14) | (14-16) | -16.18 | ≥ 18 |
| clinical symptoms | No Pain | A Little | Dull Pain | Slight Pain | Pain | Over Pain | Very Pain | Severe Pain | Painful | Unbearable Pain |
Table 2: Correspondence between PF and clinical symptoms.
The patient can receive a PF level report after the physical examination is completed using the above model. For example, a male, 56 years old, weighing 60 kg, with a lumbar flexion angle of 15 lifting a 20 kg object. The relevant parameters are shown in Table 3. His PF after calculation is 5, indicating a medium intensity of pain.
| Name | Age | Gender | Weight | Object weight | FC | Angle | p | t | d | σh2 | PF |
|---|---|---|---|---|---|---|---|---|---|---|---|
| X | 56 | male | 60kg | 20kg | 3647N | 15° | 107265Mpa | 0.02 m | 0.573 m | 916367.89MPa | 5 |
Table 3: GM5 case of multi-view data detail and PF evaluation form.
Results
Three steps of the results will be discussed as the follows.
Step I: Stress in L4 during lumbar flexion
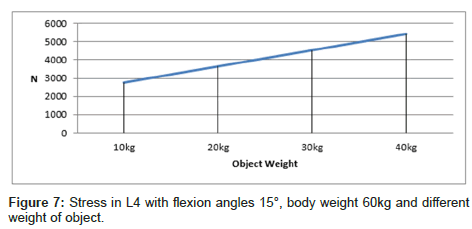
Figure 6 shows the stress in L4 under different lumbar flexion angles for a person weighing 60 kg and lifting a 20 kg object. We conclude that the stress in L4 decreases non-linearly with an increase in the flexion angle. The larger the flexion angle, the smaller the stress in L4. Figure 7 and 8 show the relationship between stress in L4 with a 15° flexion angle for different object weights (body weight is 60 kg) and different body weights (object weight is 20 kg), respectively. Due to the linear increase in weight, the stress in L4 also increases linearly in both figure 8. These results are reasonable as sown in Figures 6-8.
Step II: Stress in psoas muscles
The repeated motion of lumbar flexion causes stress oscillation in the psoas muscles. This is the reason for fatigue, swelling, pain, inflammation and even muscle damage. The stress in the psoas muscles increases first during flexion angle increase, reaching a maximum at 75° and then decreases as shown in Figure 9. The value at 75° is 2083532.39 MPa, as high as 21 times the body weight. It is observed that we have 9 times body weight stress in psoas muscles even at just a 15° flexion angle. The motion of lumbar flexion is, of course, the main culprit in the injury of psoas muscles. Figures 10 and 11 show the stress in psoas muscles with different object weights (60 kg person) and different body weights (15° angle of flexion and 20 kg weight of object), respectively. The two curves are straight lines due to the linearity variation of the weights as shown in Figures 10 and 11.
Step III: Distribution of PF vs. age and gender
Tables 4 and 5 show the pain factor distribution due to L3-L4 and L4-L5 intervertebral discs with age and gender for different positions, i.e., PF 1 for standing up and PF 2 for a 15° angle of flexion. In general, the PF of the male sub-Groups (GM) is less than the PF of the female sub-Groups (GF), as shown in Tables 4 and 5. This can also be easily seen from (Figures 12-15).
| Group G | G 1.76 (PF1) | G 5.39 (PF2) | ||||
|---|---|---|---|---|---|---|
| Age | Sub-group | Subgroup | GM | GF | GM | GF |
| 1.64 | 1.87 | 5.04 | 5.37 | |||
| 81-90 | GM8 | GF8 | 1.74 | 2.17 | 4.94 | 5.6 |
| 71-80 | GM7 | GF7 | 1.79 | 1.91 | 4.93 | 5.38 |
| 61-70 | GM6 | GF6 | 1.79 | 2.02 | 4.96 | 5.42 |
| 51-60 | GM5 | GF5 | 1.71 | 1.96 | 5.07 | 5.18 |
| 41-50 | GM4 | GF4 | 1.51 | 1.71 | 5.1 | 5.22 |
| 31-40 | GM3 | GF3 | 1.48 | 1.62 | 5.12 | 5.15 |
| 21-30 | GM2 | GF2 | 1.44 | 1.69 | 5.21 | 5.65 |
Table 4: PF 1(standing up) and PF 2(15° angle of flexion) of L3-L4.
| G | G2.3 (PF1) | G5.23 (PF2) | ||||
|---|---|---|---|---|---|---|
| Age | Sub-group | Subgroup | GM | GF | GM | GF |
| 2.25 | 2.35 | 5.05 | 5.41 | |||
| 81-90 | GM8 | GF8 | 2.64 | 2.79 | 5.21 | 5.71 |
| 71-80 | GM7 | GF7 | 2.19 | 2.63 | 5.12 | 5.49 |
| 61-70 | GM6 | GF6 | 2.34 | 2.45 | 5.12 | 5.38 |
| 51-60 | GM5 | GF5 | 2.09 | 2.13 | 5.07 | 5.28 |
| 41-50 | GM4 | GF4 | 1.98 | 2.18 | 4.96 | 5.21 |
| 31-40 | GM3 | GF3 | 2.07 | 2.14 | 4.93 | 5.21 |
| 21-30 | GM2 | GF2 | 2.13 | 2.43 | 4.94 | 5.62 |
Table 5: PF 1(standing up) and PF 2(15° angle of flexion) of L4-L5.
Figures 12-15 show that PF likely increase with age except for two sub-Groups (GF3 and GF4). This can be attributed to the fact that women in this age range are at the age of childbirth. Pregnancy and childbirth, as well as taking care of young children, may cause a certain burden.
Figures 16 and 17 show that the PF at the L4-L5 intervertebral disc is about 1.3 times larger than at L3-L4 for both males and females as shown in Figures 16 and 17.
This is commonly known; however, it can be seen from Figures 18 and 19 that there is no difference in the stress exerted on the L3-L4 and L4-L5 discs with a 15° angle of flexion while picking up a 20 kg object as shown in Figures 18 and 19.
Only sub-groups over 60 years old have slight differences, occurring in both male and female sub-groups. This may be caused by the degeneration of the intervertebral discs in the elderly and is an interesting topic discovered in this research, worthy of in-depth discussion. It shows in Table 6 and Figure 20 that this distribution is approximately normal for the main Group (G) in a 15° angle of flexion position while picking up a 20 kg object, with a mean value of 5.23 and a standard deviation of 0.487 for the pain factor. The number of persons within one standard deviation of the pain factor accounts for 74% of the total. The range of two standard deviations accounts for 97% and three standard deviations account for 99%. The data obtained shows that the female PF reaches level 7 at most, in a 15° angle of flexion position while picking up a 20 kg object. The stress acting on the psoas muscle is more than 12 times the body weighvt. Similarly, the male PF level is also 7, as shown in Figure 20. Both cases indicate a very painful level according to Table 2.
| Pain Factor | 4 | 5 | 6 | 7 | Total |
|---|---|---|---|---|---|
| Number of Person(s) | 25 | 1042 | 323 | 10 | 1400 |
Table 6: Distribution of the pain factor of main group G at L3-L4 in 15 angle of flexion position.
Discussion
1. Since circumferential stress is typically applicable to stress distribution within closed pressure vessels, there are discrepancies with the current situation:
• Even though the left and right psoas major muscles each cover 180° of the lateral sides of the lumbar spine, they are still independent of each other and do not form a closed system.
• The pressure exerted by the intervertebral discs is independent and not continuous, which introduces inevitable errors when evaluating stress amplification.
• Accurately analyzing the existing errors will be a direction for future research on this topic.
2. It is advisable to incorporate boundary element analysis into this work, which is expected to yield better results.
3. It is recommended to develop a digital model measuring instrument that can immediately calculate the pain index once the patient’s radiological results are available, helping patients better understand their pain condition.
Conclusion
This study combines biomechanics and statistics to analyze the causes of lower back pain (hoop stress) and convert this stress into a PF. Patients receive a comprehensible pain factor for their condition rather than unintelligible data. The biomechanics portion shows that the force of the psoas muscle can reach up to 20 times the body weight due to hoop stress if one makes a 75° angle of flexion. Repeatedly performing the same movement will cause fatigue and damage to the muscle. However, this study only considers the L4 spine and facet joints for stress analysis. Other surrounding tissues such as ligaments are not considered. Boundary element analysis [19] should be added in future studies for a more accurate discussion of the forces on L4. In the statistics portion, the mean Group (G) is divided into two subgroups, male (GM) and female (GF), each further divided into seven sub-groups (GM2-GM8, GF2-GF8). Data collection, derivation and analysis were performed for patients in each sub-group. The results show that the pain factor increases with age and is higher in females than in males of the same age. This study also confirms that the stress on L4-L5 is 1.3 times that of L3-L4 when standing upright, while there is no difference in the stress of L4-L5 and L3-L4 when bending at a 15° angle to pick up a 20 kg object. This finding opens up another research direction. It is worthy to analyze the properties of the nonlinear curves mathematically to facilitate further deductions.
Acknowledgements
Sincere thanks are given to Dr. Lin Ou-Yang for providing millions of patient medical records and Mr. Dingwei Chen for Data processing.
References
- Macedo LG, Richardson J, Battie MC, Hancock M, Kwan M, et al. (2021) Back to living well: Community-based management of low back pain: A feasibility study. Pilot Feasibility Stud 7:134.
[Crossref] [Google Scholar] [PubMed]
- Cashin AG, Lee H, Traeger AC, Hübscher M, Skinner Ian W, et al. (2021) Feeling reassured after a consultation does not reduce disability or healthcare use in people with acute low back pain: A mediation analysis of a randomised trial. J Physiother 67:197-200.
[Crossref] [Google Scholar] [PubMed]
- Panah HM, Abbas M, Yazdi Z, Hayati M (2021) Comparative study of combination therapy with in acute low back pain. J Bodyw Mov Ther 27:705-709.
[Crossref] [Google Scholar] [PubMed]
- Jassi F, Del Antônio TT, Azevedo B, Moraes R, George SZ, et al. (2021) Star-shape kinesio taping is not better than a minimal intervention or sham kinesio taping for pain intensity and postural control in chronic low back pain: A randomized controlled trial. Arch Phys Med Rehabil 102:1352-1360.
[Crossref] [Google Scholar] [PubMed]
- Cogan AM, Silva MA, Brostow DP (2021) Low back pain and traumatic brain injury. Arch Phys Med Rehabil 102: 1441-1443.
- Edelen MO, Rodriguez A, Herman P, Hays RD (2021) Crosswalking the patient-reported outcomes measurement information system physical function, pain interference and pain intensity scores to the roland-morris disability questionnaire and the oswestry disability index. Arch Phys Med Rehabil 102: 1317-1323.
[Crossref] [Google Scholar] [PubMed]
- Ryynänen K, Oura P, Simula AS, Holopainen R, Paukkunen M, et al. (2021) Effectiveness of training in guideline-oriented biopsychosocial management of low-back pain in occupational health services-a cluster randomized controlled trial. Scand J Work Environ Health 47:367-376.
[Crossref] [Google Scholar] [PubMed]
- Harsted S, Nyirö Lu, Downie A, Kawchuk GN, O'Neill S, et al. (2021) Posterior to anterior spinal stiffness measured in a sample of 127 secondary care low back pain patients. Clin Biomech (Bristol) 87:105408.
[Crossref] [Google Scholar] [PubMed]
- Zou CJ, Li JH, Wu FC, Li YZ, Pan HY, et al. (2021) The effects of core stability training in nurses with nonspecific low back pain. Medicine (Baltimore) 100: e26357.
[Crossref] [Google Scholar] [PubMed]
- Kaneko T, Takano Y, Inanami H. (2021) One-year clinical outcome or after full-endoscopic interlaminar lumbar discectomy for isthmic lumbar spondylolisthesis: Two case reports. Medicine (Baltimore) 100: e26385
[Crossref] [Google Scholar] [PubMed]
- Takasaki H, Kawazoe S, Miki T, Chiba H, Godfrey E, et al. (2021) Development and validity assessment of a Japanese version of the Exercise Adherence Rating Scale in participants with musculoskeletal disorders. Health Qual Life Outcomes 19:169.
[Crossref] [Google Scholar] [PubMed]
- Tsuboi Y, Oka T, Nakatsuka K, Isa T, Ono R, et al. (2021) Effectiveness of workplace active rest programme on low back pain in office workers: A stepped-wedge cluster randomised controlled trial. BMJ open 11:e040101.
[Crossref] [Google Scholar] [PubMed]
- Lu Yongtao, Cheng Liangliang, Zhu Hanxing (2021) Influence of nucleotomy on the load sharing in the spinal facet joint under the loading scenarios of different human postures. Med Eng Phys 93:35-41.
[Crossref] [Google Scholar] [PubMed]
- Yılmaz E (2021) The determination of the efficacy of neural therapy in conservative treatment-resistant patients with chronic low back pain. Spine (Phila Pa 1976) 46: E752-E759.
[Crossref] [Google Scholar] [PubMed]
- Beer FP, Johnston ER, DeWolf JT, Mazurek DF (2015). Mechanics of Materials. McGraw Hill. ISBN: 9870073398235.
- Yao YY (2009) Integrative levels of granularity. Human-centric information processing through granular modeling. Berlin: Springer-Verlag.
- Yao J (2010) Human-inspired granular computing//Novel Developments in Granular Computing: Applications for Advanced Human Reasoning and Soft Computation. Hershey: IGI Global.
- Bock D, Velleman P, Veaux RD (2023) The stats modelling the world, AP Statistic Textbook, 4th Edition, Pearson.
- L.J. Young, M.L. Chen, 2020, “Three Different Approaches to Analysis Cracked Ring with Opposite Concentrated Loads”, Journal of Physics, 1952.
Citation: Young LJ, Chen Yu, Chen Y, et al. (2025) A Biomechanics Analysis of Diagnosing Chronic Lumbagos. Diagnos Pathol Open 10:250.
Copyright: © 2025 Young LJ, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution and reproduction in any medium, provided the original author and source are credited.
Select your language of interest to view the total content in your interested language
Share This Article
Open Access Journals
Article Usage
- Total views: 9091
- [From(publication date): 0-0 - Dec 19, 2025]
- Breakdown by view type
- HTML page views: 8913
- PDF downloads: 178