Research Article Open Access
A Vague Set Based Model for Regional Blood Supply and Demand Balance Adjustment
Zhu M*, Hu HY, Wang J and Zheng ZWInstitute of Blood Transfusion, Chinese Academy of Medical Sciences & Peking Union Medical College, Chengdu, China
- Corresponding Author:
- Zhu M
Institute of Blood Transfusion
Chinese Academy of Medical Sciences & Peking Union Medical College
Chengdu, China
Tel: 86-18982061715
E-mail: zhuming100@163.com
Received date: September 28, 2013; Accepted date: January 21, 2014; Published date: January 28, 2014
Citation: Zhu M, Hu HY, Wang J, Zheng ZW (2014) A Vague Set Based Model for Regional Blood Supply and Demand Balance Adjustment. J Biomim Biomater Tissue Eng 19:122. doi:10.4172/1662-100X.1000122
Copyright: © 2014 Zhu M, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Biomimetics Biomaterials and Tissue Engineering
Abstract
For the collection and clinical usage quantities of regional blood changing randomly, it is hard to efficiently adjust regional blood supply and demand balance extent with quantitative way. To solve this problem to some extent, a vague set based adjustment model is proposed. Blood stock level of regional blood center being chosen as expressing indicator and the ideal blood stock level interval as criteria, and considering the fuzzy characters of the indicator being subject to its criteria interval, vague set similarity measure function is applied to found a vague set based measure function for regional blood supply and demand balance extent. With the introduction of adjustment factor, derived from the measure
function, an adjustment model for regional blood supply and demand balance is established. With the application of the model, and referring to the literature published blood stock operation data of several regional blood centers in China, a determination method of the aimed lower and upper limit of blood center stock control level is obtained. The aimed lower and upper limit of blood center stock control level can be an operable reference to blood center stock operation, which is helpful for regional blood center to effectively manage its blood stock level according to different regional blood supply and demand balance goal.
Keywords
Blood supply; Supply and demand; Vague set; Similarity measure
Introduction
According to the principle of blood supply and demand balance, it would be the sign of regional blood being at supply and demand equilibrium state that regional blood center stock’s real level waves around its ideal level. For the collection and clinical usage quantities of regional blood are all impacted by many complicated factors, it is hard to control a blood center stock’ real level close to an exact ideal level all the time, and the related cost is usually large, a more practical and effective method is that, let a blood center stock level changing in a reasonable interval. However, a problem is emerging, what kind of blood center stock level interval is reasonable, that is, what kind of blood center stock level interval can satisfy the requirement of regional blood supply and demand equilibrium. At present, studies on regional blood supply and demand balance mostly focus on concept and idea, and study on the concrete model for regional blood supply and demand balance adjustment is seldom published. The following are several relevant representative research works published in the literature. Brodheim and Prastacos [1] constructed a Markov chain based model. With the application of the model, regional blood allocation strategies can be gained. Kopach et al. [2] developed a red blood cell stock management system based on a queuing model, and analyzed the efficiency of the model with simulation method. Dijk et al. [3] combined stochastic dynamic programming with simulation to develop a novel approach. The approach can deal with the tradeoff between outdating and shortages of blood platelet production.
In this paper, a vague set based model is proposed for regional blood supply and demand balance adjustment with quantitative way. Blood stock level of regional blood center is chosen as expressing indicator and the ideal blood stock level interval as criteria, and considering the fuzzy characters of the indicator being subject to its criteria interval, vague set similarity measure function is applied to found a vague set based measure function for regional blood supply and demand balance extent. With the introduction of adjustment factor for regional blood supply and demand balance, derived from the measure function, an adjustment model for regional blood supply and demand balance is established. With the application of the model, and referring to the literature published blood stock operation data of several regional blood centers in China, a determination method of the aimed lower and upper limit of blood center stock control level is obtained. The aimed lower and upper limit of blood center stock control level can be an operable reference to blood center stock operation, which is helpful for regional blood center to effectively manage its blood stock level according to different regional blood supply and demand balance goal. For the complexity of regional blood supply and demand balance adjustment, the adjustment model proposed in this paper is still simple, there still exists many aspects necessary to be improved further, in future research, some relevant impact factors, such as blood center operation cost and even blood center operation officer’s risk preference etc. might also be integrated into the model, which would make the model more practical and effective.
Methods
With respect to the quantitative description of blood stock’s real level waving around its ideal level, the expression of fuzzy concept is involved, therefore, Vague sets theory that Gau and Buehrer put forward in the year 1993 is introduced [4].
Definition: Let X be a space of points (objects), with a generic element of X denoted by x [4]. A vague set V in X is characterized by a truth-membership function tv and a false-membership function fv.tv(x) is a lower bound on the grade of membership of x derived from the evidence for x, and fv(x) is a lower bound on the negation of x derived from the evidence against x. tv(x) and fv(x) both associate a real number in the interval [0,1] with each point in X , wheretv(x) +fv(x) ≤ 1. That is tv: X → [0,1], fv: X → [0,1]. This approach bounds the grade of membership of x to a subinterval [tv(x), 1-fv(x)] of [0,1]. In other words, the exact grade of membership μv(x) of x may be unknown, but is bounded by tv(x) < μv(x)< 1- fv(x), where tv(x) +fv(x) ≤ 1.
Let A and B be two vague sets in the universe of discourse X, if there are following characters with M(A, B): (a) 0 ≤ M (A, B) ≤ 1, (b) M(A, B) = M(B, A), (c) M(A, B) = 1 ↔ A=B, M(A, B) is called as the similarity degree between vague sets A and B [5].
In this paper, the following similarity measure function brought forward by Chen is used for the measure of regional blood supply and demand balance extent, and also for the formation of regional blood supply and demand balance adjustment model [6].
Let x=[tx,1-fx] be a vague value, where tx∈ [0,1], fx ∈ [0,1], and tx + fx ≤ 1. Then, the score of x can be evaluated by the score function
S shown as S(x) = tx-fx, where S(x) ∈ [-1,1]. Let 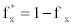 , then
we can see that
, then
we can see that 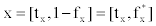 . In this case, we can see that
. In this case, we can see that 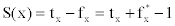 .
.
Let X and Y be two vague values, 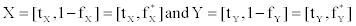 . The similarity degree between the vague
values X and Y, marked as M, can be evaluated by the function (1) [6],
. The similarity degree between the vague
values X and Y, marked as M, can be evaluated by the function (1) [6],
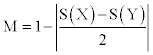 (1)
(1)
Where 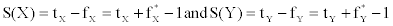 . In Equation 1, M ∈ [0,1]. M value being higher, vague values X and Y
are more similar.
. In Equation 1, M ∈ [0,1]. M value being higher, vague values X and Y
are more similar.
Results
With the blood stock level of regional blood center being chosen as expressing indicator and the ideal blood stock level interval as criteria, basing on the application of vague sets similarity measure function, a measure function for regional blood supply and demand balance extent is achieved, further with the introduction of adjustment factor, a model for regional blood supply and demand balance adjustment is constructed. By the application of the function and the model, and referring to the literature published blood stock operation data of several regional blood centers in China, a choosing method of adjustment factor and a determination method of the aimed lower and upper limit of blood center stock control level are gained.
For there exist 4 types of blood, and the supply and demand quantities of each blood type varies differently in the course of regional blood center stock management, the function and the model proposed in this paper are mainly aimed at each specific blood type.
Measure function for regional blood supply and demand balance extent
Supposing the indicator of regional blood center stock level of each
blood type being marked as yi, the blood type is indexed by i(i=1,2,3,4),
respectively representing 4 blood types of A, B, O and AB. And there
exist different regional blood center stock level state set of blood type i,
marked as Yi={yi,j}, the state is indexed by j(j=1,2,...., n). Concerning the
measure for regional blood supply and demand balance extent of blood
type i, supposing there is a vague value 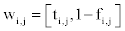 of regional
blood supply and demand balance state of blood type i, which is related to blood stock level state yi,j of blood type i. And the vague value of
regional blood supply and demand equilibrium state of blood type i
represented by the ideal value yi,m of yi,j is .
of regional
blood supply and demand balance state of blood type i, which is related to blood stock level state yi,j of blood type i. And the vague value of
regional blood supply and demand equilibrium state of blood type i
represented by the ideal value yi,m of yi,j is .
For the similarity between regional blood supply and demand balance state of blood type i represented by the real value of yi,j and its equilibrium state represented by the ideal value yi,m of yi,j can express the similar extent between the two states, the similarity may be defined as regional blood supply and demand balance degree, marked as Ei,j. Referring to Equation 1, Ei,j Ei,j can be calculated by Equation 2.
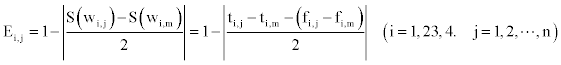 (2)
(2)
In Equation 2, Ei,j ∈ [0,1]. Ei,j Value being higher, the state of regional blood supply and demand balance of blood type i is better; On the contrary, the state is worse.
If the clinical usage proportion weight of blood type i in a region is marked as ωi, the regional blood supply and demand balance degree Ej of state j can be calculated by Equation 3.
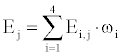 (3)
(3)
In Equation 3, Ej ∈ [0,1]. Ej value being higher, the state of regional blood supply and demand balance is better; On the contrary, the state is worse.
Depending on Ej value interval [0,1], a recommended evaluation standard for regional blood supply and demand balance state can be founded as Table 1.
| E | Supply and Demand Balance State | Supply and Demand Balance State Evaluation |
|---|---|---|
| 1.00 | Equilibrium | Good |
| [0.80,1.00) | Near Equilibrium | Normal |
| [0.60,0.80) | A little Deficient or Excessive Supply | Critical |
| [0.30,0.60) | Deficient or Excessive Supply | Abnormal |
| [0.00,0.30) | Extremely Deficient or Excessive Supply | Bad |
Table 1: Recommended evaluation standard for regional blood supply and demand balance state.
Model for regional blood supply and demand balance adjustment
Let the minimum value, ideal interval lower limit, ideal value, ideal
interval upper limit, and maximum value of yi,j are marked respectively as 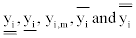 .
.
Referring to Equation 2, regional blood supply and demand balance extent of blood type i can be measured by yi,j, so if the real value of yi,j being changed to an object by adjustment, accordingly regional blood supply and demand balance state of blood type i is also controlled to a related goal. If the aimed value of yi,j is yi,k, and the ideal value is yi,m, depending on Equation 2, the regional blood supply and demand balance degree Ei,k of blood type i can be calculated by Equation 4.
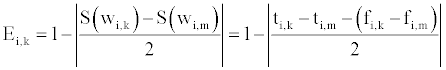 (4)
(4)
In Equation 4, Ei,k ∈ [0,1]. Ei,k value being higher, the aimed state of regional blood supply and demand balance of blood type i is better, On the contrary, the state is worse.
Generally, in regional blood center stock operation, as the aimed value yi,k of yi,j being closer to its ideal value yi,m, the operation may become more difficult, that is, in the value interval [0,1] of regional blood supply and demand balance degree Ei,k of blood type i, as Ei,k increasing, the regional blood supply and demand balance adjustment of blood type i may become more difficult. If an adjustment factor, marked as R, is introduced to express this kind of adjustment effect, basing on the above understanding, there may be the following function relationship between Ei,k and the adjustment factor Ri of blood type i.
Ei,k=f(Ri)=lg(Ri) (5)
In Equation 5, Ri ∈ [1,10]. Ri value being higher, the related adjustment strength produced by Ri is stronger, On the contrary, the related adjustment strength is weaker.
Equation 6 derived from Equation 5 can determine adjustment factor Ri value of blood type i according to regional blood supply and demand balance degree Ei,k of blood type i.
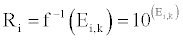 (6)
(6)
Basing on Equation 4 and Equation 5, the model for regional blood supply and demand balance adjustment of blood type i can be deduced as the following.
If the aimed adjustment value yi,k of yi, being less than the lower limit of yi ideal interval, that is, 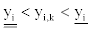 the vague value wi,k of yi,k is,
the vague value wi,k of yi,k is, 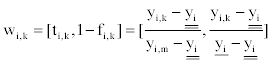 And the vague value wi,m of the
ideal value yi,m of yi is wi,m=[ti,m,1-fi,m]=[1,1]. Hence integrating Eqs. (4)
and (5), the relationship function at the interval
And the vague value wi,m of the
ideal value yi,m of yi is wi,m=[ti,m,1-fi,m]=[1,1]. Hence integrating Eqs. (4)
and (5), the relationship function at the interval 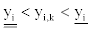 between
the aimed adjustment value yi,k of yi and the adjustment factor Ri of
blood type i can be constructed as Equation 7.
between
the aimed adjustment value yi,k of yi and the adjustment factor Ri of
blood type i can be constructed as Equation 7.
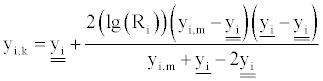 (7)
(7)
Similarly, if the aimed adjustment value yi,k of yi being at the following intervals 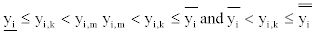 the
relationship functions between the aimed adjustment value yi,k of yi and
the adjustment factor Ri of blood type i can also be obtained respectively.
the
relationship functions between the aimed adjustment value yi,k of yi and
the adjustment factor Ri of blood type i can also be obtained respectively.
With the integration of the above, supposing the aimed adjustment
lower limit and upper limit of blood center stock level of blood type
i being marked as 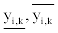 respectively, the model for regional
blood supply and demand balance adjustment of blood type i can be
established as Equation 8.
respectively, the model for regional
blood supply and demand balance adjustment of blood type i can be
established as Equation 8.
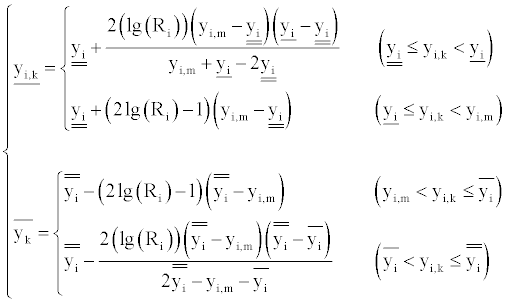 (8)
(8)
Basing on Equation 8, according to adjustment factor Ri value,the aimed lower limit 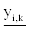 and upper limit
and upper limit 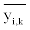 of blood center stock
level of blood type i can be calculated. The aimed lower limit
of blood center stock
level of blood type i can be calculated. The aimed lower limit 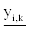 and
upper limit
and
upper limit 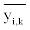 of blood center stock level of blood type i are clear and
operable instructions to regional blood center stock operation.
of blood center stock level of blood type i are clear and
operable instructions to regional blood center stock operation.
The choosing method of adjustment factor
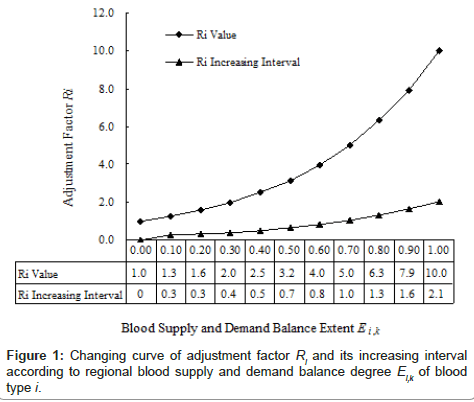
By Equation 6, the changing curve of adjustment factor Ri and its increasing interval according to regional blood supply and demand balance degree Ei,k of blood type i can be got as Figure 1.
Depending on Figure 1, Table 1 and Equation 3, according to different adjustment goal of regional blood supply and demand balance, a recommended choosing method for adjustment factor Ri value of blood type i is formed as Table 2.
| Adjustment Goal | Recommended Interval for the Choosing of Ri Value | Aimed Interval for Ei,k |
|---|---|---|
| Reducing extremely deficient supply | [1,4] | [0.00,0.60] |
| Almost eliminating deficient supply | [4,7] | [0.60,0.85] |
| Tending to equilibrium or equilibrium | [7,10] | [0.85,1.00] |
| Almost eliminating excessive supply | [4,7] | [0.60,0.85] |
| Reducing extremely excessive supply | [1,4] | [0.00,0.60] |
Table 2: Recommended choosing method for adjustment factor Ri value of blood type i.
The determination method of the aimed lower and upper limit of blood center stock level
Referring to the literature published blood stock operation data of several regional blood centers in China, the parameters values of the model for regional blood supply and demand balance adjustment can be recommended.
While using Equation 8 to determine the aimed adjustment lower
limit 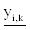 and upper limit
and upper limit 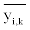 of blood center stock level of blood type
i, it is necessary to determine the parameters in Equation 8 which are
the minimum value
of blood center stock level of blood type
i, it is necessary to determine the parameters in Equation 8 which are
the minimum value 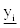 ideal interval lower limit
ideal interval lower limit 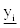 ideal value yi,m, ideal interval upper limit
ideal value yi,m, ideal interval upper limit 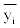 and maximum value
and maximum value 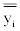 of yi. Referring
to the published blood stock operation data of several regional blood
centers in China in the literature [7-11], and supposing the average
blood usage quantity per day in a blood center during a selected
period of blood type i being marked as Ci(U), the parameters values in
Equation 8 can be recommended as Table 3.
of yi. Referring
to the published blood stock operation data of several regional blood
centers in China in the literature [7-11], and supposing the average
blood usage quantity per day in a blood center during a selected
period of blood type i being marked as Ci(U), the parameters values in
Equation 8 can be recommended as Table 3.
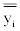 |
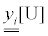 |
yi,m[U] | 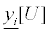 |
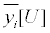 |
| 1 Ci | 4Ci | 7 Ci | 10 Ci | 14 Ci |
Table 3: The recommended values of parameters in Eq. 8.
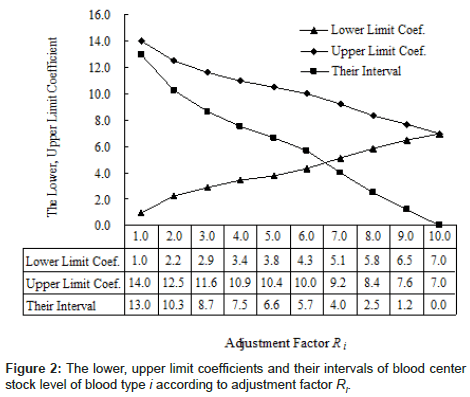
Basing on Table 2, concerning different adjustment goals, a series of related adjustment factor Ri values can be chosen. By Table 3 and Equation 8, according to the chosen adjustment factor Ri values, the aimed lower and upper limit coefficients and their intervals of blood center stock level of blood type i can be got as Figure 2.
In blood stock management practice of a regional blood center, the lower, upper limit of blood center stock level values of blood type i can be obtained by the lower, upper limit coefficients in Figure 2 being multiplied with the average blood usage quantity Ci(U) per day of blood type i in the blood center.
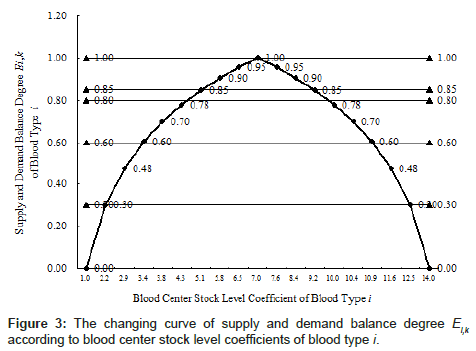
From the aimed lower and upper limit coefficients of blood center stock level of blood type i in Figure 2, by Equation 2, the related regional blood supply and demand balance degree Ei,k of blood type i can be got as Figure 3.
Analysis and discussion
(1) Considering the complexity of relationship between adjustment factor and regional blood supply and demand balance extent, the related relationship function is designed to be logarithm function, which produces the adjustment effect like that, by the same step length the adjustment factor value is raised in interval [1,10], but the increases of blood center blood stock level and regional blood supply and demand balance degree is becoming smaller and smaller. The designed adjustment effect may reflect that, the closer the real state of regional blood supply and demand balance to its ideal state, the more difficult the adjustment operation is, therefore, the less improvement of the state the same rising of adjustment factor can produce.
(2) From Tables 1 and 2 and Figure 1, we can see the following adjustment effect which is made by the designed logarithm function. If the aimed adjustment goal is “Almost eliminating excessive supply” or “Almost eliminating deficient supply”, the possibly choosing value of adjustment factor is at interval [4,7], the possibly achieved regional blood supply and demand balance degree is at interval (0.60,0.85), and the possibly achieved regional blood supply and demand balance state is “A little deficient or excessive supply” or “Near equilibrium”. If the aimed adjustment goal is “Tending to equilibrium or equilibrium”, the possibly choosing value of adjustment factor is at interval [7,10], the possibly achieved regional blood supply and demand balance degree is at the interval of (0.85,1.00), and the possibly achieved regional blood supply and demand balance state is “Near equilibrium” or “Equilibrium”.
(3) From Figures 2 and 3, we can see the following adjustment result which is made by the adjustment model. With the adjustment factor Ri value being chosen from 1.0 up to 10.0, the lower limit coefficient of blood center stock level of blood type i increases from 1.0 up to 7.0, while the upper limit coefficient decreases from 14.0 up to 7.0, consequently the interval between lower and upper limit coefficient declines quickly from 13.0 up to 0.0, and the regional blood supply and demand balance degree of blood type i is raised from 0.00 up to 1.00, in the course of the regional blood supply and demand balance degree of blood type i tending to 1.00, the gain becomes less and less with the same step length the adjustment factor Ri value being raised.
(4) From Figure 3, some suggestion for regional blood center to control blood stock level can be recommended as the following. If it is expected that the regional blood supply and demand balance degree of blood type i be not less than 0.60, the horizontal line marked 0.60 is critical line, hence the lower, upper limit coefficient of blood center stock level of blood type i might be more than 3.4 and less than 10.9 respectively. If it is expected that the supply and demand balance extent of blood type i be not less than 0.85, the horizontal line marked 0.85 is critical line, the lower, upper limit coefficient of blood center stock level of blood type i might be more than 5.1 and less than 9.2 respectively. Concerning other regional blood supply and demand balance degree values of blood type i, the lower, upper limit coefficient of blood center stock level of blood type i is determined by the same method. In blood stock management practice of a regional blood center, the lower, upper limit of blood center stock level control values of blood type i can further be got by the lower, upper limit coefficients being multiplied with the average blood usage quantity Ci(U) per day of blood type i in the blood center.
Conclusion
The vague set based model for regional blood supply and demand balance adjustment is proposed. The model works with the help of a standardized adjustment factor, and the adjustment factor being integrated into the model is depended on the application of a vague set similarity measure function. Because of the design of logarithm function relationship between regional blood supply and demand balance extent and adjustment factor, the adjustment by the model can be practical and exact to some extent, moreover, the aimed lower and upper limit of blood center stock control level got from the model can be an operable and clear reference to blood center stock operation, which is helpful for regional blood center to effectively adjust its blood stock level according to different regional blood supply and demand balance goal. Although the adjustment effect of the model is comparatively satisfied, necessarily the model should be improved further, for the state of regional blood supply and demand balance is impacted by many complicated factors, such as the dynamic character of blood collection and usage in a region, and even blood center operation officer’s risk preference, blood center operation cost, etc. In future study, more efforts should be focused on developing more proper methods to integrate the relevant impact factors into the model, so as to make the model more practical and effective.
References
- Brodheim E, Prastacos GP (1979) The Long Island blood distribution system as a prototype for regional blood management. Interfaces 9: 3-20.
- Kopach R, Balcioglu B, Carter M (2008) Tutorial on constructing a red blood cell stock management system with two demand rates. Eur J Operational Res 185: 1051-1059.
- Dijk N, Haijema R, Wal J, Sibinga CS (2009) Blood platelet production: a novel approach for practical optimization. Transfusion 49: 411-420.
- Gau WL, Buehrer DJ (1993) Vague sets. IEEE Transactions on Systems, Man, and Cybernetics 23: 610-614.
- Zhou XG, Zhang Q (2005) Comparison and improvement on similarity measures between vague sets and between elements. Journal of System Engineering 20: 613-619.
- Chen SM (1995) Measures of similarity between vague sets. Fuzzy Sets and Systems 74: 217-223.
- Guo KS, Li FQ, Feng N, Zhang JG (2006) Study on method of setting the best stockpile quantity in blood station, Chinese Health Quality Management 13: 71-73.
- Feng Y, Qiao ZY, Zhang LX (2007) Optimize blood stock management to assure effective using. Chin J Blood Transfusion 6: 518.
- Sun JL, Shan B, Wang YT, Yang FL, Zhou CL (2005) Study on strategy of blood stock adjustment. Chin J Blood Transfusion 1: 85-87.
- Li Y, Wang MY, Pan ZR (2007) Quality control method├ó┬?┬?s application in analysis of blood best stock quantity. Chin J Blood Transfusion 1: 52-53.
- Mo B (2007) Blood best stock quantity analysis├ó┬?┬?s application in the non-remunerated blood donation. J Clin Transfus Lab Med 9: 157-158.
Relevant Topics
Recommended Journals
Article Tools
Article Usage
- Total views: 13508
- [From(publication date):
February-2014 - Aug 29, 2025] - Breakdown by view type
- HTML page views : 8853
- PDF downloads : 4655