Artificial Neural Network Modeling of Ball Mill Grinding Process

Veerendra Singh; P K Banerjee; S K Tripathy; V K Saxena; R Venugopal

doi:10.4172/2168-9806.1000106

ISSN: 2168-9806

Journal of Powder Metallurgy & Mining

Make the best use of Scientific Research and information from our 700+ peer reviewed, Open Access Journals that operates with the help of 50,000+ Editorial Board Members and esteemed reviewers and 1000+ Scientific associations in Medical, Clinical, Pharmaceutical, Engineering, Technology and Management Fields.

Meet Inspiring Speakers and Experts at our 3000+ Global Conferenceseries Events with over 600+ Conferences, 1200+ Symposiums and 1200+ Workshops on Medical, Pharma, Engineering, Science, Technology and Business

Artificial Neural Network Modeling of Ball Mill Grinding Process

Veerendra Singh^1*, P K Banerjee¹, S K Tripathy¹, V K Saxena² and R Venugopal²

¹Research and Development, Tata Steel, Jamshedpur-831001, India

²Indian School of Mines, Dhanbad, Jharkhand-826004, India

*Corresponding Author:: Veerendra Singh
Research and Development, Tata Steel
Jamshedpur-831001, India
E-mail: veerendra.singh@tatasteel.com

Received Date: December 27, 2012; Accepted Date: February 15, 2013; Published Date: February 21, 2013

Citation: Veerendra Singh, Banerjee PK, Tripathy SK, Saxena VK, Venugopal R (2013) Artificial Neural Network Modeling of Ball Mill Grinding Process. J Powder Metall Min 2:106. doi: 10.4172/2168-9806.1000106

Copyright: © 2013 Veerendra Singh, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Visit for more related articles at Journal of Powder Metallurgy & Mining

View PDF Download PDF

Abstract

Grinding consumes around 2% of the energy produced in the world but existing methods of milling are very inefficient and use only 5% of the input energy for real size reduction rest is consumed by machine itself. Chrome ores are comminute, filtered, pelletized and sintered to use into submerged arc furnace for ferrochrome production. Variation in ore properties affects the particle size distribution during milling. Artificial neural network based model is developed to predict the particle size distribution of ball mill product using grinding data available for difference in grindability of Sukinda chromite ores. Input variables for model were ball size, ball load, ball-ore ratio, grinding time. Output was particle size distribution (+75 μm, -75 μm, +38 μm; -38 μm). Three different kinds of mathematical models have been compared to predict the particle size distribution. Finally a neural network based model was found most accurate. Dynamic artificial neural network model does not require any material constant and optimizes the mathematical correlation with better accuracy in a dynamic process. This methodology can be used to develop an online system to predict the ball mill performance to improve the performance of grinding circuit in mineral, metal and cement industry.

Keywords

Milling; Ball mill; Particle size; Artificial Neural Network; Regression

Introduction

Milling is a vital unit operation in various material processing operations and consumes around 2% of the energy produced in the world [1,2]. It dictates the cost economics of mineral, cement, power, pharmaceutical and ceramic industries. Grinding is an important unit operation for chrome ore pelletisation process. Chromite ore along with 5% coke is milled in the wet ball mill and filtered ore cake is mixed with bentonite and used for production of green pellets. Pellet quality and pelletisation subprocesses (filtering, pelletisation and sintering) depend on the characteristics of the ball mill product size. Physical properties of ores, especially hardness, friability and grindability play a vital role in grinding to achieve the desired fineness for pelletisation process [3,4]. Ore particle size, shape and roughness influence the particle packing and moisture required for green ball formation [5]. Improper particle size distribution results in poor pellet qualities and reduced plant throughput as well. Ball mill operation is a complex process and there is no unanimous mathematical relationship given in the literature for all kind of materials. Various attempts have been made to relate the milling parameters and particles fineness but most of these models required a material constant for different materials. Material constant vary significantly with change in ore properties and it restricts the success of the models [6-10]. Artificial neural network is a faster and reliable tool to develop a mathematical model to predict the process variability in such cases. It is not a new technique for mineral processing and has already been explored for various mineral processing operations in past [11,12].

Present study is focused to model the ball operation of a pelletisation plant to predict the ball mill product size distribution with changed operating conditions. The mathematical model developed using artificial neural network has been compared with various conventional models and results are compared for actual and predicted size distributions.

Problem Definition

Problem statement

Performance ball milling depends on ore properties and process variables. Ore properties depend on the geological and geographical characteristics. It is not possible to develop a single mathematical model for all kind of ores. Various mathematical models have been developed using the material constants but a limited success has been achieved. It is very difficult for a static model to consider the variation in the ores characteristics along the vertical and horizontal location of ore block. This problem becomes more critical when a blend of different kind of materials grounded in a ball mill for pelletisation purposes. Artificial neural network can be a useful technological development which can consider all the uncertainties to develop a dynamic model without bothering about the material constants and geography of ore block. In this study an Artificial Neural Network (ANN) based neural network model has been developed to predict the particle size distribution of a ball mill product using the lab data. Developed model uses ball size, ball-ore ratio, ball load and grinding time as the input variables and particle size distribution (<75 μm, <38 μm) as an output measurements.

Data analysis

Experimental data were collected from lab to develop the mathematical model. A statistical analysis has been carried out to see the variable interdependence. Details are given in the Table 1 and 2. Experiments were carried out using a ball mill of 38 cm diameter×38 cm length and Chrome Ore (-3 mm), Coke Fine (-1 mm) and at a pulp density of 70% solid and 50 rpm ball mill speed.

Input Variable	Level
Ball Size (mm) - BS	40,25,18
Ball Load (kg)- BL	22.50, 67.50
Ball- Ore Charge ratio-R	1,3
Grinding Time (minutes)-t	15, 30, 60, 90

Table 1: Input variables.

Variables	<75micron		<38micron		38-75micron
Variables	Cc	p	Cc	p	Cc	p
40mm(BS₄₀)	-0.05	0.67	-0.06	0.62	-0.04	0.74
25mm (BS₂₅)	-0.04	0.75	-0.05	0.71	0.02	0.99
18mm(BS₁₈)	0.14	0.26	0.18	0.16	0.03	0.80
Ball load (BL)	0.49	0.00	0.53	0.00	0.24	0.05
Ball: Ore (R)	0.21	0.09	0.23	0.05	0.07	0.56
Time (t)	0.73	0.00	0.69	0.00	0.61	0.00

Cc = Correlation coefficient; p: p-value

Table 2: Correlation Matrix for input and output variables.

Material characterisation

The test work was carried out using the chromite ore samples collected from the feed ore of a pelletisation plant. These chromite ores are of friable in nature with friable and broken particles. The bond work index of ores was 6 kWh/ton. These ore contain 30, 26, 12 and 14%, Cr₂O₃, Fe, SiO₂ and Al₂O₃, respectively.

Mathematical Modelling

Banerjee model

Experiments were carried out to optimize ball load, ball size, ball ore ratio, grinding time, pulp density and ball mill rpm. It was found that ball mill rpm and pulp density are having least effect on the product size distribution. Hence, they drop these variables for mathematical model development. Mathematical model developed by Banerjee is given in equation (1) and (2). This model is based on ball diameter (Db), ball-ore ratio (R) and grinding time (t).

S75=19.30-0.31 Db+12.60 R+0.47 t (1)

S38 = 4.39-16Db+9.52R+0.31t (2)

S75-Percentage of particles below 75 micron

S38-Percentage of particles below 38 micron

Statistical modeling

Increased computational facilities enable us to carry out different kind of data analysis in a quick session with better reliability. A Statistical model has been developed using more number of input variables than the Banerjee et al. [1] used. Statistical model is given in equation 3.

S75=23.3-0.11*BS₄₀-0.89*BS₂₅-0.98*BS₁₈+0.43*BL+3.98*R+0.43*t- (3)

S38=-0.39-0.017* BS₄₀+0.002*BS₂₅+0.015* BS₁₈+0.35*BL+2.71*R+0.31*t- (4)

ANN modeling

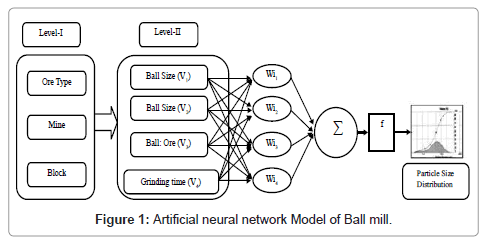
Artificial neural networks have proved their applicability in various data mining application. These are generally used for function approximation, classification, and pattern reorganization problems. Artificial neural networks are directed graph consisting nodes with interconnecting synaptic and activation links. The weight given to different links decides the critical effect of the different input pairs on the outputs. Each neuron holds three important elements that are: connecting links (weights), adder (summing agent) and an activation function, which control the amplitude of output. Structure of an Artificial Neural Network can be classified into three groups based on the arrangement of neurons and the connection patterns of the layers: feed forward, feedback, self-organizing [13].

Feed forward back propagation neural network: In these networks information enter at the inputs layer and passes through the network without any feedback between layers. The training is mainly undertaken using the back propagation-based learning algorithms. In the processing units of feed forward inputs X_i are multiplied by weights W_ji for a hidden node h_j; summation of all the W_ji×X_i is then added toa bias value θ_ji and finally operated by a suitable transfer function (f). Similar operations are repeated for varying number of hidden layers in order to find out suitable network architecture. The operations can be written as

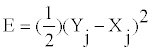
Equation

Hidden layers contribute to the output nodes through a linear operation. The output Y can be written as

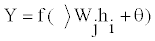
Equation

Where W_j and θ’ are new sets of weights and bias values, respectively. In the process of learning, the error of the calculated by Eq. (5) or predicted output in relation to the actual output is back propagated to adjust all the weight and bias values.

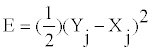Equation (5)

There are several algorithms to optimize the error values. A number of different kinds of back propagation learning algorithms have been proposed, such as an on-line neural-network learning algorithm for dealing with time varying inputs, fast learning algorithms based on gradient descent of neuron space, and the Levenberg– Marquardt algorithm [14,15]. In current work, the performance index was predicted by resilient feed forward back propagation neural network algorithm. Multi-layered feed forward neural network is shown in figure 1 is used to estimate the particle size distribution. After performing the basic statistical operations training and testing datasheet was prepared in which 64 datasets were used for training and 10 datasets were used to test these networks. The transforms functions are used to relate the input and outputs of the network. Tansig, logsig and purlin are commonly used transfer function for prediction and classification. In current problem better results were achieved by using tansig for first layer and linear for last two layers. The training data set for neural network was primed using principal component analysis and retains only those components, which contribute more than 5% to the variance in the data set. Feed forward neural networks were trained for 5000 epochs and number of neurons was optimized along with hidden layer for all the training algorithms. The targeted error was kept 0.1 which is usually found acceptable for these kinds of problems.

Figure 1: Artificial neural network Model of Ball mill.

Results and Discussion

Prediction accuracy of mathematical models

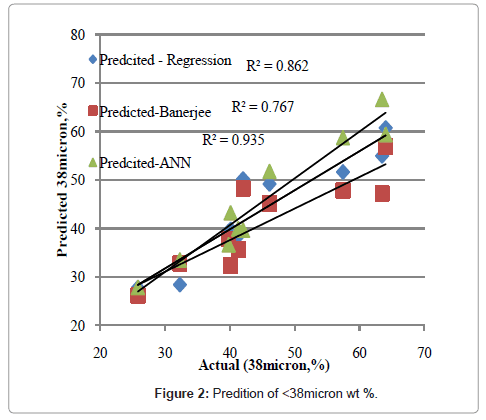
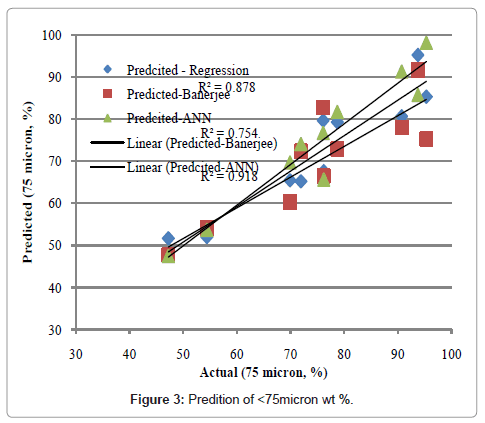
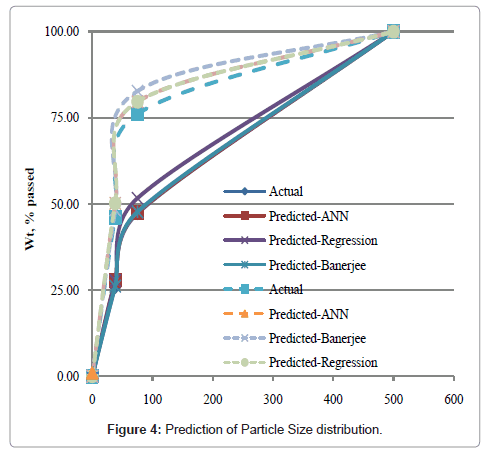
Mathematical models developed were tested for medium grade chromite ores from open cast mine of northern block. Figures 2 and 3 shows the comparative prediction accuracy of all three models. Graphs show that R-square value vary between 0.76 and 0.93 and it is highest for artificial neural network model to predict the particle of <38 micron. In case of particle <75 microns, it was found that R-square value vary between 0.75 and 0.92 and it was also highest for artificial neural network model. It was also observed that all the modes are poor predictor near to limits of process variables but neural network is predicting more accurately than all other models. Using these models particles < 75 and <38 micron were predicted and particle 38-75micron was calculated using these two values. A predicted particle size distribution curve and actual particle size distribution curve was plotted and shown in figure 4. It is shown for minimum (set 1) and maximum (set 2) particle size distribution. It reveals that for finer size distribution ANN and regression is performing similar but for coarser size ANN performs better.

Figure 2: Predition of <38micron wt %.

Figure 3: Predition of <75micron wt %.

Figure 4: Prediction of Particle Size distribution.

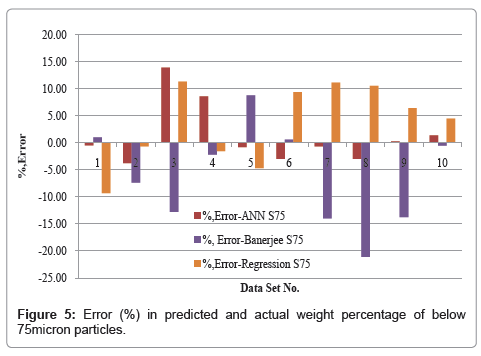
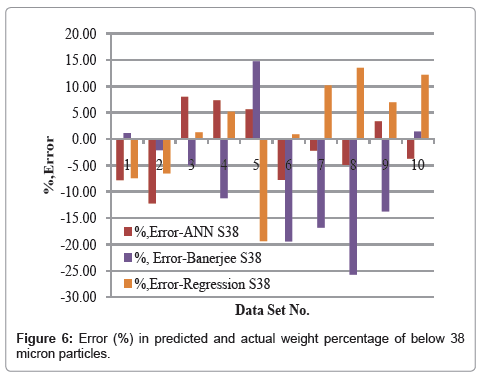
R square of predicted and actual values can not exhibit many insigts of model. So, percentage error in these values also studied to provide important patterns. It shows that regression model underpredict whereas Banerjee model overpredict the weight percenatge of <75 mirocn size particles. Highest percentage errors were 22.1,12.3,13.5% for Banerjee, regression and neural network model, respectively. Error distribution for both the particle sizes is given in figures 5 and 6.

Figure 5: Error (%) in predicted and actual weight percentage of below 75micron particles.

Figure 6: Error (%) in predicted and actual weight percentage of below 38 micron particles.

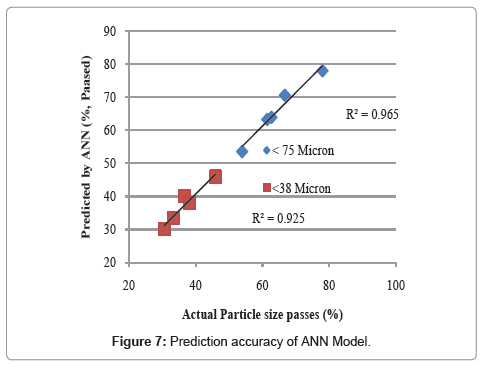
Effect of ore quality variation on ANN model

Variation in quality of ores with the depth and length of mine is a commonly encountered problem for mineral processing plants. Samples of the hard ore from the different mine location of the same ore body was collected and provided as an input for the developed neural network model and found that accuracy of the prediction was very higher for these case. Prediction accuracy was 0.92 and 0.96 for <38 and <75micron size particles, respectively. It is shown in figure 7. The reason behind this was the neural network found out an optimum multidimensional surface using the soft ores and same space was reconstructed using the data of hard grade which enable it to optimize the weights of hidden layers to get the best prediction for new data sets.

Figure 7: Prediction accuracy of ANN Model.

Conclusions

Milling is an importan unit operation for pelletisation of chorme ores. But development of a sigle integrated empherical model to estimate the variation in ore fineness due chaged feed blend properties is a diiffcult task. Artificial neural network is suitable tool for this problem and can provide very accurate and faster prediction about the change in particle size distribution due to variation in ore properties. It was found that it is better than the statstical models and predcit the effect of chaged ore quality with higher accuracy. This is a dynamic model and do not require any material constant to achieve the based prediction accuracy which help it to get better accuracy with variation in ore quality and milling parameters. This setup can be used for online monitoring of the milling performance of comminution plant for beneficiation and pelletisation process to minimze the energy losses with improved processs effecieny.