Comparison Evaluation of Periimplant Alveolar Crest Stress/Strain Distribution Ability Depending on Alveolar Bone Density: Mathematical Model

Anna Yu Poghosyan^1*, Tigran A Muradyan² and Norik E Grigoryan³

¹Department of Maxillofacial and ENT Surgery "Heratsy" ΓΆΒ?Β?1 University Hospital, Armenia

²Muradent Dental Clinic, Ejmiatsin, Armenia

³A.I. Alikhanyan National Science Laboratory, Yerevan, Armenia

Corresponding Author:

Dr. Anna Yu. Poghosyan
Department of Maxillofacial and ENT Surgery
"Heratsy" ΓΆΒ?Β?1 University Hospital
13 Avag Petrosyan Str., 18 apt
Yerevan 0001, Armenia
Tel: +374 91 474 169
E-mail: anna.yu.poghosyan@gmail.com

Received date: March 12, 2015; Accepted date: June 05, 2015; Published date: June 09, 2015

Citation: Poghosyan AY, Muradyan TA, Grigoryan NE (2015) Comparison Evaluation of Periimplant Alveolar Crest Stress/Strain Distribution Ability Depending on Alveolar Bone Density: Mathematical Model. J Interdiscipl Med Dent Sci 3:178. doi: 10.4172/2376-032X.1000178

Copyright: © 2015 Poghosyan AY, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Visit for more related articles at JBR Journal of Interdisciplinary Medicine and Dental Science

Abstract

The aim of this study was to evaluate the biomechanical response of the periimplant bone stress/strain ability to loading forces depending on bone type. The mathematical model analysis was chosen for the present study as it has proved to be a useful tool in estimating stress distribution in the contact area of the implant with surrounding bone. The calculations were aimed to show the differences of strain forces (F) distribution ability depending of bone types (D1, D2, D3, D4). The different bone types with the same V volume arise different strain forces. When comparing these values we see that and differ from in 3 and 5 times respectively, so and types of bones have 3 and 5 times less strain distribution ability than the type bone.

Keywords

Crestal bone resorption; Strain analysis; Alveolar bone density; Mathematic model

Introduction

Maintenance of peri-implant bone support is one of the most important criteria for implant therapy success [1]. A clinical studies shows that a progressive bone loss around the implant occurs when it undergoes functioning and may lead to implant failure [2]. The greatest stress after the osseointegration healing period occurs at the crest [3,4].

Unlike the natural tooth the implant doesn’t have periodont. Periodont is one of the main elements that provide teeth with amortization. In the presence of a dental implant, compared to a natural tooth, the stress and strain fields are altered for several reasons, including the lack of cushioning provided by the periodontal ligament, morphological differences between an implant and a natural tooth, and the differences in the material properties of the implant as compared to a natural tooth [5]. Alterations in loading conditions can result in bone remodeling, according to Wolff ’s law [6], which states that the adaptation of bone morphology is regulated by mechanical loading. To study long-term bone morphology, mathematical models of bone remodeling have been developed and were later adopted to predict dental implant-induced bone remodeling [7,8]. In addition to implant design, crestal bone geometry, and placement site, strain levels in periimplant bone can be affected by alveolar bone quality and implant insertion depth and can result in different bone maintenance characteristics [9].

Excessive functional load or traumatic occlusion may overstress the implant system and lead to peri-implant marginal bone loss [10,11]. Manz MC reported that crestal bone loss after successful bone integration was related directly to the bone density. If the stresses applied to an implant exceeds the physiological limitation of bone density around the implant, implant failure may occur [12,13].

Primary implant stability and bone density are variables that are considered essential to achieve predictable osseointegration and longterm clinical survival of implants. Information about the influence of bone quality on stress distribution in an implant-supported crown is limited [14]. There are also limited Finite Element Analysis studies considering the influence of implant diameter and length, implant design, bone quality on stress distribution around implants [15-18].

The purpose of this study was to evaluate the biomechanical response of the periimplant bone stress/strain ability to loading forces depending on bone type by the mathematical modeling.

Materials and Methods

The mathematical model analysis was chosen for the present study as it has proved to be a useful tool in estimating stress distribution in the contact area of the implant with surrounding bone. So, theoretical model of bone strain distribution ability is proposed.

During absolutely elastic deformation the developed F force is equal to:

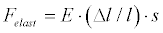
Where E - is Young’s modulus, (Δl / l )· s unit defines the volume of linear deformation of the body (i.e. when one of the trimester features changes during deformation).

Young’s modulus ( E ) depends on the type of the material and expresses the module of the force developed in one unit volume of the material during one unit deformation. It is expressed by the following formula:

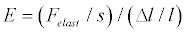
where, s - is the surface area of the material, Δl / l is the length change for one unit of length, F_elast is the elastic force exerted on an object under tension

Young’s coefficient is different for different types of bones [19]. E.g.

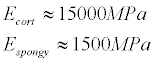
But, for example, for periodont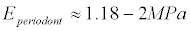

However, according to Lin et al. [11], the relationship between Young’s modulus and density for the cortical and cancellous bone is not necessarily identical. In continuum mechanics, the mechanical stress tensor consists of six independent components. As a result, these equations are, of course, approximate and theoretically meaningful, but they allow to make a conclusion that bones of different types ( D₁ − D₄ according to K. Mish) have different strain distribution ability.

The elasticity force depends on two criteria: the type of the material and its primary volume (as the material with great volume has a greater possibility to be deformed).

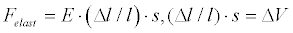
consequently

The next calculations are aimed to show the differences of strain forces distribution ability in dependents of bone types

Thus, D₁ type of bone is almost 100% cortical bone. So,

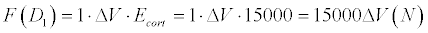
D₂ type of bone is defined as 50% cortical and 50% spongy bone compound, so

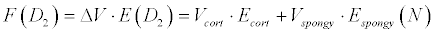
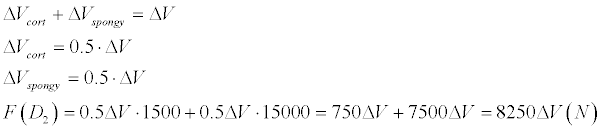
D₃ type of bone is characterized as 25% cortical and 75% spongy bone, in the result

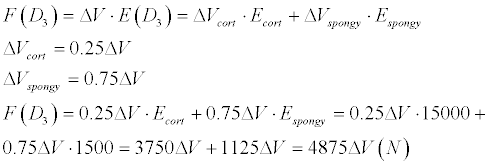
D₄ type of bone is defined by minimal number of cortical layers and mainly by fragile spongy layer.

We’ll calculate supposing 10% cortical layer and90% spongy layer.

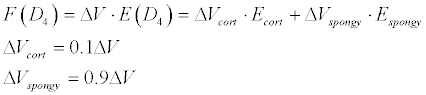
Consequently follows

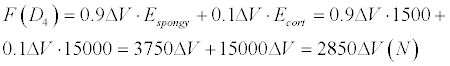(N)

So, we can conclude, that in the different bone types with the same V volume the different strain forces arise.

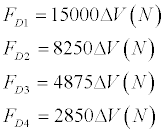
For the linear absolutely elastic deformation we have got approximately the following values:

When comparing these values we can see that FD₃ and FD₄ differ from FD₁ in 3 and 5 times respectively. We can see that D₃ and D₄ types of bones have 3 and 5 times less strain distribution ability than the D₁ type bone. So, if in case of D₁ ,D₂ bone types minimal amount of the neck surrounding bone should be 1mm, in case of D₄ bone type this amount should be not less than 2-3 mm.

Discussion

The use of dental implants for the treatment of partial or complete edentulism has become an effective alternative in recent decades [20]. In a manner similar to that of an orthopedic implant, a dental implant serves as a load-bearing device that not only sustains masticatory forces, but also transfers loads to periimplant bone. Load transfer depends on successful healing of the osteotomy and osseointegration, which is characterized as a direct structural and functional connection between the bone and the implant surface [21,22]. The mechanical situation at the osseointegrated implant-bone interface is quiet different to that at the natural tooth-bone interface [23]. That is the reason why the implant and the neighboring bone are exposed to different stresses under bite forces as compared to the natural tooth. The ratio of amount of movements of a tooth in a healthy periodontium to that of a osseointegrated dental implant has been estimated to be between 10: 1 and 100: 1 [24]. This potential difference in movement amount could result in gradual loss in crestal bone around the implant [25]. The masticatory forces induce axial forces and bending moments, which could result in stress on the implant as well as the surrounding bone. Bone tissue is known to remodel its structure in response to mechanical stress. Variations in the internal state of stress in the bone determine whether constructive or destructive remodeling will take place. Wolff first suggested that there is a relationship between bone structures and applied loads [6]. The bone acts as if has some sensors that can measure the internal load and activate the bone cells to make the bone grow or resorb [26].

Stresses induced by occlusal loads are initially transferred from the implant to the cortical bone, while a small amount of remaining stress is spread to the cancellous bone. It is also possible that higher strain values are observed in cortical bone as it presents a higher elastic modulus when compared with trabecular bone and thus has a greater ability to transfer stress [19,27,28]. There are scientific works with mathematical models and Finite Element Analysis where calculated influence of loading forces, abutment taper, implant length and width, insertion depth, periimplant bone type on stress distribution [5,9,15,27-29].

In all of this studies authors proposed the models in which they have supposed some definite loading force (axial or oblique) from 100 to 400 N and Von Mises stresses and strains (ε) have evaluated. In our study we have tried to calculate the ability of bone withstand to formed strains and stresses in depends on bone types. Our calculations have shown that the D₁ and D₂ bone types can endure more loading, than D₃ and D₄ if they have the same periimplant bone volume. But, if we can increase bone volume around implant either by bone augmentation or by choosing narrow implant so, we can increase bone ability to withstand loading forces.

Conclusion

Taking the calculations into consideration we can assume that the choice of the implant diameter should depend also on bone qualities. The bones with different bone quality have different strain distribution ability, properly, different facility to dump the loading force.

D₃ and D₄ bone types have less strain distribution ability, therefore, for implant loading forces compensation or forces dumping they needs in more bone thickness around implant, than D₁ or D₂.

References

1. Astrand P, Engquist B, Dahlgren S, Gröndahl K, Engquist E, et al. (2004) Astra Tech and Brånemark system implants: a 5-year prospective study of marginal bone reactions. Clin Oral Implants Res 15: 413-420.
2. Misch CE (1995) Early crestal bone loss etiology and its effect on treatment planning for implants. Postgrad Dent 2: 3-17.
3. Clelland NL, Ismail YH, Zaki HS, Pipko D (1991) Three-dimensional finite element stress analysis in and around the Screw-Vent implant. Int J Oral Maxillofac Implants 6: 391-398.
4. Rasouli Ghahroudi A, Talaeepour A, Mesgarzadeh A, Rokn A, Khorsand A, et al. (2010) Radiographic Vertical Bone Loss Evaluation around Dental Implants Following One Year of Functional Loading. J Dent (Tehran) 7: 89-97.
5. Chou HY, Müftü S, Bozkaya D(2010) Combined effects of implant insertion depth and alveolar bone quality on periimplant bone strain induced by a wide-diameter, short implant and a narrow-diameter, long implant. J Prosthet Dent 104: 293-300.
6. Wolff J (1986) The law of bone remodeling. Springer.
7. Carter DR, Fyhrie DP, Whalen RT (1987) Trabecular bone density and loading history: regulation of connective tissue biology by mechanical energy. J Biomech 20: 785-794.
8. Li J, Li H, Shi L, Fok AS, Ucer C, et al. (2007) A mathematical model for simulating the bone remodeling process under mechanical stimulus. Dent Mater 23: 1073-1078.
9. Baggi L, Cappelloni I, Di Girolamo M, Maceri F, Vairo G (2008) The influence of implant diameter and length on stress distribution of osseointegrated implants related to crestal bone geometry: a three-dimensional finite element analysis. J Prosthet Dent 100: 422-431.
10. Ricci G, Aimetti M, Stablum W, Guasti A (2004) Crestal bone resorption 5 years after implant loading: clinical and radiologic results with a 2-stage implant system. Int J Oral Maxillofac Implants 19: 597-602.
11. Li Q, Li W, Lin D, Rungsiyakull P, Swain M (2009) Bone Resorption Induced By Dental Implants with Ceramics Crowns. J Australian Ceramic Soc 45: 1-7.
12. Manz MC (1997) Radiographic assessment of peri-implant vertical bone loss: DICRG Interim Report No. 9. J Oral Maxillofac Surg 55: 62-71.
13. Misch CE (1999) Progressive bone loading. In: Misch CE, editor. Contemporary implant dentistry.
14. Sevimay M, Turhan F, Kiliçarslan MA, Eskitascioglu G (2005) Three-dimensional finite element analysis of the effect of different bone quality on stress distribution in an implant-supported crown. J Prosthet Dent 93: 227-234.
15. Holmes DC, Loftus JT (1997) Influence of bone quality on stress distribution for endosseous implants. J Oral Implantol 23: 104-111.
16. Petrie CS, Williams JL (2005) Comparative evaluation of implant designs: influence of diameter, length, and taper on strains in the alveolar crest. A three-dimensional finite-element analysis. Clin Oral Implants Res 16: 486-494.
17. Qian L, Todo M, Matsushita Y, Koyano K (2009) Effects of implant diameter, insertion depth, and loading angle on stress/strain fields in implant/jawbone systems: finite element analysis. Int J Oral Maxillofac Implants 24: 877-886.
18. Tada S, Stegaroiu R, Kitamura E, Miyakawa O, Kusakari H (2003) Influence of implant design and bone quality on stress/strain distribution in bone around implants: a 3-dimensional finite element analysis. Int J Oral Maxillofac Implants 18: 357-368.
19. Borchers L, Reichart P (1983) Three dimensional stress distribution around an implant at different stages of interface development. J Dent Res 62: 155-159.
20. Romeo E, Lops D, Margutti E, Ghisolfi M, Chiapasco M, et al. (2004) Long-term survival and success of oral implants in the treatment of full and partial arches: a 7-year prospective study with the ITI dental implant system. Int J Oral Maxillofac Implants 19: 247-259.
21. Adell R, Lekholm U, Rockler B, Brånemark PI (1981) A 15-year study of osseointegrated implants in the treatment of the edentulous jaw. Int J Oral Surg 10: 387-416.
22. Schenk RK, Buser D (1998) Osseointegration: a reality. Periodontol 2000 17: 22-35.
23. Chapman RJ (1989) Principles of occlusion for implant prostheses: guidelines for position, timing, and force of occlusal contacts. Quintessence Int 20: 473-480.
24. Richter EJ (1989) Basic biomechanics of dental implants in prosthetic dentistry. J Prosthet Dent 61: 602-609.
25. van Steenberghe D, Lekholm U, Bolender C, Folmer T, Henry P, et al. (1990) Applicability of osseointegrated oral implants in the rehabilitation of partial edentulism: a prospective multicenter study on 558 fixtures. Int J Oral Maxillofac Implants 5: 272-281.
26. Burr DB, Martin RB, Schaffler MB, Radin EL (1985) Bone remodeling in response to in vivo fatigue microdamage. J Biomech 18: 189-200.
27. Meijer HJ, Starmans FJ, Steen WH, Bosman F (1993) A three-dimensional, finite-element analysis of bone around dental implants in an edentulous human mandible. Arch Oral Biol 38: 491-496.
28. Shelat S, Kularashmi BS, Annapoorani H, Chakravarthy R (2011) Effect of two different abutment types on stress distribution in the bone around an implant under two loading conditions. J Dent Implant 1: 80-85.
29. Yokoyama S, Wakabayashi N, Shiota M, Ohyama T (2005) Stress analysis in edentulous mandibular bone supporting implant-retained 1-piece or multiple superstructures. Int J Oral Maxillofac Implants 20: 578-583.