Dynamic Energy Detection Approach for Spectrum Sensing in Cognitive Radio Networks

¹ME (ECE), Electronics and Communication Engineering Branch, UIET, Panjab University, Chandigarh

²Assistant Professor,Electronics and Communication Engineering Branch, UIET, Panjab University, Chandigarh

^*Corresponding Author:

Pulkit Sharma
ME (ECE), Electronics and Communication Engineering Branch
UIET, Panjab University
Chandigarh
E-mail: pulkitsharmay2k@gmail.com

Visit for more related articles at International Journal of Advance Innovations, Thoughts & Ideas

Abstract

The current spectrum management scheme is leading to underutilization of spectrum. Cognitive Radio Networks solves the problem of spectrum scarcity by using dynamic spectrum management. Using dynamic spectrum management secondary users can use the licensed spectrum opportunistically. Cognitive Radio Networks can be implemented practically only after detecting those primary bands which are not used by licensed primary user. These free primary bands are technically called spectrum holes and detecting these spectrum holes is called spectrum sensing. New technique for detecting spectrum holes in primary band is proposed in this paper. Various techniques used for spectrum sensing are also described in this paper. Performance of the proposed spectrum sensing method is evaluated under different parameters. Spectrum sensing results for proposed method are compared with the spectrum sensing methods proposed previously. Simulation results shows that the spectrum sensing results for the proposed scheme are better than the previously proposed methods. 

Keywords

Cognitive Radio Networks, Dynamic Spectrum Management, Spectrum Sensing.

Introduction

Cognitive Radio, the term was initially coined by Joseph Mitola [1] in 1999 and now it is a major research topic. The precious radio spectrum is an important resource which is used for all wireless communication and is depleting day by day. The initial research showed that the spectrum is not limited, but it is not managed well, so the real problem occurs with spectrum management. With initial research it comes out that the entire licensed spectrum is not used but most of the spectrum is left unused, only a few part of the licensed spectrum allocated by the regulating agencies is utilized. This leads to underutilization of spectrum and this problem of underutilization of spectrum can be solved using smart wireless networks called Cognitive Radio Networks. In Cognitive Radio Networks dynamic spectrum management is used and thus spectrum is utilized effectively. Cognitive Radios are smart radios and are called so due to their awareness about surroundings, they can sense the radio spectrum in the surrounding and can decide to use the free channels from licensed primary spectrum. Dynamic Spectrum Access thus leads to effective utilization of the available spectrum. In these networks the licensed users which originally have the spectrum are called primary users while the users which use that licensed primary spectrum opportunistically are called secondary users or Cognitive Radio users. The main feature of these smart networks is to use spectrum holes in an opportunistic manner without causing any harmful interference to the primary user. The spectrum utilization efficiency of wireless communication is thus increased. The working of these networks is divided into four parts [2] Spectrum Sensing, Spectrum Decision, Spectrum Sharing, and Spectrum Mobility. The first part is spectrum sensing which is most important, deals with finding the free licensed primary spectrum i.e. finding a spectrum hole in the licensed signal which can be used by the secondary users to transmit their signal. This paper deals with spectrum sensing in Cognitive Radio Networks only because it is the most important part. Only after sensing the free spectrum correctly, it can be used opportunistically. To sense the spectrum holes different methods for spectrum sensing are proposed in literature like Energy Detection [3] – [7], Cyclostationary Based Sensing [8], Waveform Based Sensing [9], Multi taper Method for Spectrum Sensing [10], Frequency Domain Entropy Based Detector [11], Matched Filtering [12], Radio Identification Based Sensing [13] . Some other Spectrum Sensing methods include Hough Transform; Wavelet Transform based estimation and time frequency analysis. Hough Transform can be used to detect any type of signal with a periodic pattern also [14]. Energy Detection is most commonly used method for spectrum sensing, because it is very fast. Energy Detector have some limitations also, it cannot differentiate between signal and noise.

The paper is arranged in five more sections. In Section II preliminaries and channel model is discussed, section III gives description about Energy Detection. New method called Dynamic Energy Detection is described in Section IV. Simulation results are discussed in Section V and finally the paper is concluded in Section VI.

Preliminaries and Channel Model

In order to sense the spectrum whether the channel is free or not we have to consider some channel model or the Here the channel model is taken in accordance with [15] which states that

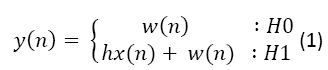      (1)

Where

y(n) = Signal received at secondary receiver.

h = Channel Gain.

x(n) = Primary signal transmitted through a wireless channel.

w(n) = Additive Gaussian White Noise is a Gaussian Random Variable with zero mean and Power Spectral Density (PSD) Ɲ0

i.e. w(n) ≈ Ɲ(0, Ɲ0)

Binary Hypothesis:

H0: Signal Absent

H1 : Signal Present

Energy Detection

Energy Detection is the most common way of spectrum sensing because of its simplicity and low implementation complexities [3-5]. In an Energy Detector the received signal is first pre filtered by an ideal Band Pass Filter which has Bandwidth ‘W’ and then its output is squared and integrated(summed) over a time interval ‘T’(‘N’) to get the test statistic ‘G’. This test statistic is then compared with the threshold ‘λ’.

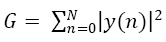      (2)

White noise is modelled as a zero mean Gaussian random Variable (GRV) with variance σ_ω² i.e.

w(n)= Ɲ(0,σ_ω²)      (3)

To make a simple analysis let the signal let the signal can also be modelled as a zero mean Gaussian Random Variable (GRV)

s(n)=σ_s²      (4)

Due to these assumptions the decision metric M follow a chi – square distribution with 2N degrees of freedom Χ²_2N and hence can be modelled as

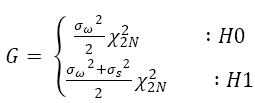      (5)

Energy Detector has few challenges

• Selection of threshold for detection primary users.

• Energy Detector has poor performance under low Signal to Noise Ratio (SNR).

• Energy Detector is unable to differentiate interference primary user and noise.

• Energy Detector doesn’t work efficiently for spread spectrum signals.

Two metrics called Probability of Detection (P_D)and Probability of False Alarm (P_F)are used to calculate the performance of spectrum sensing in Cognitive Radio Networks. Probability of false alarm means the test decides that the primary user is present when it is not present actually while Probability of Detection is detection of an actual primary signal. Both these probabilities are written mathematically in equations (6) and (7) [16].

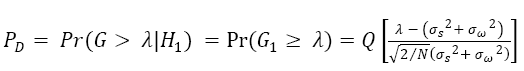      (6)

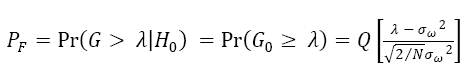      (7)

σ_ω² = Gaussian White Noise Variance.

σ_s² = Primary Signal Variance.

N = Number of Samples of received Primary Signal.

λ = Decision Threshold.

Q( ) = Standard Gauss Complementary Accumulated Function.

Choosing the threshold ‘λ’ is very important for the receiver and it is chosen such that a certain amount of False Alarm Rate can be achieved. For a given value of Probability of False Alarm the threshold can be calculated according to relation.

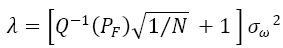      (8)

N = Number of Samples of received Primary Signal.

σ_ω² = Gaussian White Noise Variance.

P_F = Probability of False Alarm.

Q^-1( ) = Inverse of Standard Gauss Complementary Accumulated Function.

Dynamic Energy Detection

Energy detection is described in detail in the previous sections. To increase the effectiveness of Energy Detection a new scheme called Dynamic Energy Detection is proposed in this paper. In this scheme of Energy Detection difference values of square of test statistics are taken. Squared previous value is subtracted from the squared value of current sample. In this technique we get a series of statistics by subtracting squared previous test statistic from squared current statistics according to equation given below.

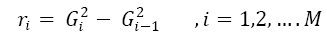      (9)

In this technique mean value as the average change of Energy Detection result. The test statistic for this technique is,

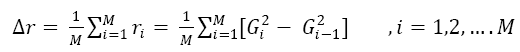      (10)

Thus sample of a result are compared with test statistic calculated above and thus the final decision statistic is

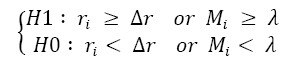      (11)

This is the dynamic energy detection scheme proposed for spectrum sensing in Cognitive Radio Networks. Performance of squared energy detection spectrum sensing is calculated using two metrics Probability of Detection (P_D) and Probability of False Alarm (P_F) and these two metrics are calculated according to the values given in equation (6) and (7).

Simulation Results

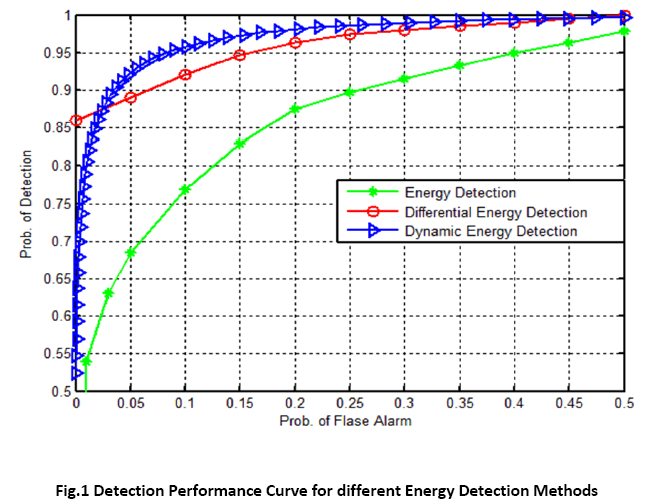
The proposed system is simulated in MATLAB7 Release 2010a. The simulation is done for the proposed dynamic energy detection. The parameters used to evaluate the performance of proposed method are probability of detection and probability of false alarm. The simulation results are shown in figure 1 shown below.

Figure 1: Detection Performance Curve for different Energy Detection Methods.

Here in figure 1 the green ‘*’ line corresponds to a traditional energy detector. The red ‘o’ line corresponds to the differential energy detector proposed in literature. The blue line in this figure shows the performance of the dynamic energy detection proposed in this paper. From the simulation results it is clear that the proposed scheme performs better than the traditional energy detection methods proposed in literature.

Conclusion

Energy Detection is described in detail in the starting of this paper. The problem with the traditional Energy Detection is that it cannot differentiate between the noise and primary signal. A novel energy detection approach called squared energy detection is proposed in this paper. The performance of proposed squared energy detection is calculated using performance metrics Probability of detection and Probability of False Alarm. In the proposed method of spectrum sensing the test statistic is compared with the mean value of the difference between the squares of two samples. The chances of detection of signal increase in this method because the test statistic now is compared with the new threshold which is according to the strength of received signal. The simulation results showed that the proposed scheme performs better than the previously proposed schemes in the literature.

References

1. Mitola, J. and J. Maguire, G. Q., “Cognitive radio: making software radios more personal,” IEEE Personal Communications Magazine, vol. 6, no. 4, Aug. 1999, pp. 13–18.
2. I.F. Akyilidiz, Won – Yeol Lee, Mehmet C. Vuran and ShantidevMohanty, “ A survey on Spectrum Management in Cognitive Radio Networks,” IEEE Communications Magazine, April 2008.
3. SamanAtapattu, ChinthaTellambura and Hai Jiang, “Energy Detection Based Cooperative Spectrum Sensing in Cognitive Radio Networks,” IEEE Transactions on Wireless Communications, vol. 10, no. 4, April 2011, pp. 1232–1241.
4. G. Ganesan and Y. Li, “Agility improvement through cooperative diversity in cognitive radio,” in Proc. IEEE Global Telecomm. Conf. (Globecom), vol. 5, St. Louis, Missouri, USA, Nov./Dec. 2005, pp. 2505–2509.
5. G. Ganesan and Y. Li, “Cooperative spectrum sensing in cognitive radio networks,” in Proc. IEEE Int. Symposium on New Frontiers in Dynamic Spectrum Access Networks, Baltimore, Maryland, USA, Nov. 2005, pp. 137–143.
6. D. Cabric, A. Tkachenko, and R. Brodersen, “Spectrum sensing measurements of pilot, energy, and collaborative detection,” in Proc. IEEE Military Commun. Conf., Washington, D.C., USA, Oct. 2006, pp. 1–7.
7. D. Cabric, S. Mishra, and R. Brodersen, “Implementation issues in spectrum sensing for cognitive radios,” in Proc. Asilomar Conf. on Signals, Systems and Computers, vol. 1, Pacific Grove, California, USA, Nov. 2004, pp. 772–776.
8. N. Han, S. H. Shon, J. H. Chung, and J. M. Kim, “Spectral correlation based signal detection method for spectrum sensing in IEEE 802.22 WRAN systems,” in Proc. IEEE Int. Conf. Advanced Communication Technology, vol. 3, Feb. 2006.
9. H. Tang, “Some physical layer issues of wide-band cognitive radio systems,” in Proc. IEEE Int. Symposium on New Frontiers in Dynamic Spectrum Access Networks, Baltimore, Maryland, USA, Nov. 2005, pp. 151–159.
10. Gao Hu, Wu Muqing, XuChunxiu and Wu Qianqian, “ An Improved Multitaper Method for Spectrum Sensing in Cognitive Radio Networks,” in IEEE, 2010.
11. Ya Lin Zhang, Qin Yu Zhang and TommasoMelodia, “A Frequency – Domain Entropy – Based Detector for Robust Spectrum Sensing in Cognitive Radio Networks” in IEEE Communication Letters, vol. 14, no. 6, June, 2010, pp 533 – 535.
12. R. Tandra and A. Sahai, “Fundamental limits on detection in low SNR under noise uncertainty,” in Proc. IEEE Int. Conf. Wireless Networks, Commun.and Mobile Computing, vol. 1, Maui, HI, June 2005, pp. 464 – 469.
13. T. Y¨ucek and H. Arslan, “Spectrum characterization for opportunistic cognitive radio systems,” in Proc. IEEE Military Commun. Conf., Washington, D.C., USA, Oct. 2006, pp. 1–6.
14. Y. Zeng and Y.-C. Liang, “Covariance based signal detections for cognitive radio,” in Proc. IEEE Int. Symposium on New Frontiers in Dynamic Spectrum Access Networks, Dublin, Ireland, April 2007, pp. 202–207.
15. Beibei Wang, K.J.Ray Liu and T.Charles Clancy, “Evolutionary Cooperative Spectrum Sensing Game: How to collaborate?,” IEEE Transactions on Wireless Communications, vol. 58, no. 3, March 2010, pp. 890 – 900.
16. Z. Ling-Ling,H.Jian – guo, T. Cheng – kai , “Novel Energy Detection Scheme in Cognitive Radio,” IEEE international conference on Signal Processing, Communications and Computing(ICSPCC),Sept.2011.