Review Article Open Access
Experimental Results of Phoebe Framework: Optimal Formulas for Estimating Fetus Weight and Age
Loc Nguyen1* and Thu-Hang Thi Ho21International Engineering and Technology Institute, Ho Chi Minh City Society for Reproductive Medicine, Long Xuyen city, An Giang 881092, Vietnam
2Vinh Long General Hospital, Vinh Long, Vietnam
- *Corresponding Author:
- Loc Nguyen, Ph.D., MD
Director, International Engineering and Technology Institute
Board of Directors, Ho Chi Minh City Society for Reproductive Medicine
Long Xuyen city, An Giang 881092, Vietnam
Tel: 84975250362
Fax: 975250362
E-mail: ng_phloc@yahoo.com
Received date: December 13, 2016; Accepted date: March 06, 2017; Published date: March 13, 2017
Citation: Nguyen L, Ho THT (2017) Experimental Results of Phoebe Framework: Optimal Formulas for Estimating Fetus Weight and Age. J Comm Pub Health Nursing 3:163. doi:10.4172/2471-9846.1000163
Copyright: © 2017 Nguyen L, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Community & Public Health Nursing
Abstract
Fetal age and weight estimation plays an important role in pregnant treatments. There are many estimate formulas created by combination of statistics and obstetrics. However, such formulas give optimal estimation if and only if they are applied into specified community. We proposed a so-called Phoebe framework that supports scientists to find out most accurate formulas with regard to the community where scientists do their research. Now we compose this paper that focuses on using Phoebe framework to derive optimal formulas from experimental results. In other words, this paper is an evaluation of Phoebe framework.
Keywords
Fetal age estimation; Fetal weight estimation; Regression model; Estimate formula.
Introduction
Fetal age and weight estimation is to predict the birth weight or birth age before delivery. It is very important for doctors to diagnose abnormal or diseased cases so that she/he can decide treatments on such cases [1]. This research is relevant to apply regression model into the birth estimation. Fetal ultrasound measures such as bi-parietal diameter (bpd), head circumference (hc), abdominal circumference (ac), fetal length (fl), arm volume (arm_vol), and thigh volume (thigh_vol) are recorded and considered as input sample for regression analysis which results in a regression function. This function is formula for estimating fetal age and weight according to these ultrasound measures. Note, some terminologies such as regression function, function, regression model, estimate function, estimate model and estimate formula have the same meaning.
There are many estimate formulas resulted from gestational researches [2-10]. Some of them gain high accuracy but they are only appropriate to population, community or ethnic group where such researches are done. If we apply these formulas into other community such as Vietnam, they are no longer accurate. Moreover, it is very difficult to find out a new and effective estimate formula or the cost of time and resources of formula discovery is expensive. Therefore, Nguyen and Ho [1] proposed a so-called Phoebe framework for supporting physicians and researchers to discover optimal estimate formulas. This research focuses on using Phoebe framework to derive such optimal formulas from experimental results. Note that Phoebe framework used statistic software package “Java Scientific Library” of Flanagan [11] and parsing package “A Java expression parser” of Jong [12]. The package “Java Scientific Library” is the most important in the framework. The framework is implemented by Java language [13].
Materials and Methods
As afore mentioned in the introduction section, we make experiments based on Phoebe framework in order to find out optimal formulas for estimating fetus weight and ages with note that such formulas are most appropriate to our gestational sample. We use two samples in which the first sample includes 2-dimension ultrasound measures of 1027 cases and the second sample includes 3-dimension ultrasound measures of 506 cases. Ho and Phan [14] collected these samples of pregnant women at Vinh Long General Hospital – Vietnam with obeying strictly all medical ethical criteria. These women and their husbands are Vietnamese. Their periods are regular and their last periods are determined. Each of them has only one alive fetus. Fetal age is from 28 weeks to 42 weeks. Delivery time is not over 48 h since ultrasound scan. Measures in 2-dimension sample are bpd, hc, ac, and fl. Measures in 3-dimension sample are bpd, hc, ac, fl, thigh_vol, arm_vol. The unit of bpd, hc, ac, fl is millimeter. The unit of thigh_vol and arm_vol is cm3. The units of fetal age and weight are week and gram, respectively.
As aforementioned, Phoebe framework uses regression model for birth estimation. Suppose a linear regression function Y = α0 + α1X1 + α2X2 + … + αnXn where Y is response or dependent variable and Xi (s) are regression or independent variables. Each αi is called regression coefficient. Response variable Y represents fetal weight or age. The builtin algorithm is the core of Phoebe framework, which is responsible for discover optimal regression model fastest. It is based on two heuristic conditions such as minimum condition and maximum condition. Please see article “A framework of fetal age and weight estimation” [1] for more details about the heuristic algorithm. The current implementation of the proposed algorithm establishes that the minimum threshold δ is arbitrary. It also supports non-linear regression models as follows:
Polynomial model
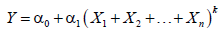
Logarithm model
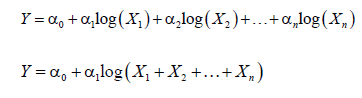
Exponent model
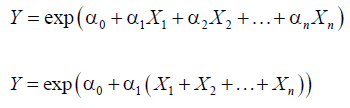
Product model
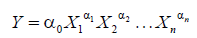
The notations “exp” and “log” denote exponent function and natural logarithm function, respectively. Most of non-linear regression models can be transformed into linear regression models. For example, given product model, following is an example of linear transformation.
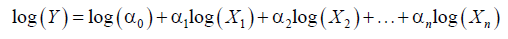
Let,
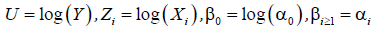
The product model becomes linear model with regard to variables U, Zi and coefficients βi as follows:
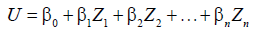
With the built-in heuristic algorithm, Phoebe framework can be totally used for any regression application beyond birth estimation.
Experimental Results
The proposed framework can produce amazing formulas. We compare our optimal formulas with the others according to metrics such as estimate correlation and estimate error range, given two aforementioned samples [14,15] collected at Vinh Long General Hospital – Vietnam. Let Y 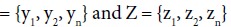 be fetal sample age/weight and fetal estimated age/weight, respectively. The estimate correlation denoted R is correlation coefficient of sample response value and estimated response value. The correlation R reflects adequacy of a given formula. The larger the R is, the better the formula is.
be fetal sample age/weight and fetal estimated age/weight, respectively. The estimate correlation denoted R is correlation coefficient of sample response value and estimated response value. The correlation R reflects adequacy of a given formula. The larger the R is, the better the formula is.

An estimate error denoted di is deviation between zi and yi
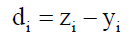
The estimate error mean denoted μ is mean of errors. The error mean μ reflects accuracy of a given formula. The smaller the absolute value of μ is, the more accurate the formula is. If μ is positive, the respective formula leans to overestimation. If μ is negative, the respective formula leans to low estimation.
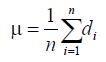
The standard deviation σ of estimate errors reflects stability of a given formula. The smaller the standard deviation σ is, the more stable the formula is.
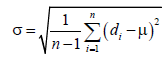
The combination of error mean μ and standard deviation σ results out a so-called error range. For example, if μ=-0.0292 and σ=1.45 then, the error range is -0.0292 ± 1.45, which means that the total average error ranges from -1.4792 = -0.0292-1.45 to 1.4208 = -0.0292+1.45. The error range reflects both adequacy and accuracy of a given formula. In general, error mean μ, error standard deviation σ, and error range are also shown in Figure 6.
Table 1 shows comparison between our best age formula and the others with 2-dimension sample. As a convention, name of each formula is the name of respective author listed in references section. For example, formula “Ho 1” is the first formula of Ho [5]. As seen in Table 1, our formula is the best with R=0.9303 and error range -0.0292 ± 1.4500 week(s).
The sign “^” denotes exponent operator. The template of formulas aims to flexibility, which can be input of any computational tool. Table 2 shows comparison between our best weight formula and the others with 2-dimension sample. As seen in Table 2, our formula is the best with R=0.9636 and error range -7.4656 ± 212.5573 grams.
Table 3 shows comparison between our best age formula and the others with 3-dimension sample. As seen in Table 3, our formula is the best with R=0.9970 and error range ± 0.2696 week.
Table 4 shows comparison between our best weight formula and the others with 3-dimension sample. As seen in Table 4, our formula is the best with R=0.9708 and error range ± 180.9803 grams.
Although our formulas are better than all remaining ones with high adequacy (large R) and high accuracy (small error range), other researches are always significant because their formulas are very simple and practical. Moreover, our formulas are not global. If they are applied into other samples collected in other communities, their accuracy may be decreased and they may not be still better than traditional formulas such as Sherpard and Hadlock. However, it is easy to draw from our experimental results that if Phoebe framework is used for the same samples with other researches, it will always produce preeminent formulas. In order to achieve global optimality with Phoebe framework, followings are two essential suggestions:
| Formula | Expression | R | Error Range |
|---|---|---|---|
| Our formula | log (age) = 2.419638109304 + 0.002011545172 * bpd + 0.000934094686 * hc + 0.005469775639 * fl + 0.001042107315 * cvb | 0.9303 | -0.0292 ± 1.4500 |
| Ho 1 | age = 331.022307583389 - 1.611773915587 * (hc + ac) + 0.002779686994 * ((hc + ac) ^ 2) - 0.000001530428 * ((hc + ac) ^ 3) | 0.9212 | 0 ± 1.5384 |
| Varol 6 | age = 11.769 + 1.275 * fl/10 + 0.449 * ((fl/10) ^ 2) - 0.02 * ((fl/10)^ 3) | 0.8949 | -1.6807 ± 1.8525 |
| Varol 1 | age = 5.596 + 0.941 * ac/10 | 0.8941 | -0.5683 ± 1.7711 |
| Varol 5 | age = 1.863 + 6.280 * fl/10 - 0.211 * ((fl/10) ^ 2) | 0.8934 | -1.5182 ± 2.1150 |
Table 1: Comparison of age estimation with 2-dimension sample.
| Formula | Expression | R | Error Range |
|---|---|---|---|
| Our formula | log (weight) = -10.047381367788 + 1.948640017621 * log(bpd) + 0.263745313905 * log(hc) + 0.601972103528 * log(fl) + 0.905523630923 * log(cvb) | 0.9636 | -7.4656 ± 212.5573 |
| Sherpard | weight = 10^(1.2508 + 0.166 * bpd/10 + 0.046 * ac/10 - 0.002646 * ac * bpd/100) | 0.9619 | -65.8121 ± 219.0392 |
| Ho 2 | weight = 10^(1.746 + 0.0124 * bpd + 0.001906 * ac) | 0.9602 | -11.5576 ± 223.5124 |
| Hadlock | weight = 10^(1.304 + 0.05281 * ac/10 + 0.1938 * fl/10 - 0.004 * ac * fl/100) | 0.9395 | -76.4960 ± 272.9474 |
| Campbell and Wilkin | weight = 1000 * exp(-4.564 + 0.282 * ac/10 - 0.00331 * ac * ac/100) | 0.9215 | 68.1261 ± 308.5728 |
Table 2: Comparison of weight estimation with 2-dimension sample.
| Formula | Expression | R | Error Range |
|---|---|---|---|
| Our formula | age = 20.759762531262 + 0.170858541042 * (thigh_vol + arm_vol) - 0.000544722555 * ((thigh_vol + arm_vol)^2) + 0.000000914897 * ((thigh_vol + arm_vol)^3) | 0.9970 | 0 ± 0.2696 |
| Ho 3 | age = 21.1148 + 0.2381 * thigh_vol - 0.001 * (thigh_vol ^ 2) + 0.000002 * (thigh_vol^3) | 0.9960 | -0.0150 ± 0.3173 |
| Ho 4 | age = 167.079078948836 - 1.553704882894 * ac + 0.005559118365 * (ac^2) - 0.000006184312 * (ac^3) | 0.8482 | 0.3723 ± 1.8985 |
Table 3: Comparison of age estimation with 3-dimension sample.
| Formula | Expression | R | Error Range |
|---|---|---|---|
| Our formula | weight = -3617.936174872692 + 0.513171264916 * hc + 1.960175553517 * ac + 39.804645398677 * bpd + 17.016936212461 * fl + 8.366404260334 * thigh_vol + 5.828808072346 * arm_vol | 0.9708 | -0.0001 ± 180.9803 |
| Ho 5 | weight = -3306 + 55.477 * bpd + 13.483 * thigh_vol | 0.9663 | -0.0072 ± 194.0956 |
| Lee 3 | weight = exp(0.5046 + 1.9665 * log(bpd/10) - 0.3040 * (log(bpd/10)^2) + 0.9675 * log(ac/10) + 0.3557 * log(arm_vol)) | 0.9620 | 247.8761 ± 206.1607 |
| Lee 5 | weight = exp(2.1264 + 1.1461 * log(ac/10) + 0.4314 * log(thigh_vol)) | 0.9514 | 289.2660 ± 234.0763 |
| Lee 2 | weight = exp(-3.6138 + 4.6761 * log(ac/10) - 0.4959 * (log(ac/10)^2) + 0.3795 * log(arm_vol)) | 0.9472 | 316.4974 ± 242.7964 |
| Ho 6 | weight = -882.7049 + 73.9955 * thigh_vol - 0.497 * (thigh_vol^2) + 0.0014 * (thigh_vol^3) | 0.9385 | -7.5001 ± 260.4596 |
| Lee 4 | weight = exp(4.7806 + 0.7596 * log(thigh_vol)) | 0.9298 | 737.4932 ± 344.1904 |
| Lee 1 | weight = exp(4.9588 + 1.0721 * log(arm_vol) - 0.0526 * (log(arm_vol)^2)) | 0.9281 | 867.0836 ± 309.5779 |
| Chang | weight = 1080.8735 + 22.44701 * thigh_vol | 0.9229 | 456.5168 ± 298.2517 |
Table 4: Comparison of weight estimation with 3-dimension sample.
- Experimenting on Phoebe with many samples.
- Adding more knowledge of pregnancy study, ultrasound technique, and obstetrics into Phoebe framework. In other words, the additional knowledge will be modeled as constraints of the built-in algorithm.
These suggestions go beyond this research. For my opinion, we cannot reach absolutely the global optimality because Phoebe framework focuses on local optimality with specific communities. Essentially, the suggestions only alleviate the weak point of built-in algorithm in global optimality.
Conclusion
According to experimental results, there is no doubt that Phoebe framework produces optimal formulas with high adequacy and accuracy; please see Tables 1-4 for more details. However we also recognize the weak point of our research is that the built-in algorithm can lose some good formulas due to the heuristic conditions. The suggestive solution is to add more constraints into such conditions; please read the article “A framework of fetal age and weight estimation” [1] for more details.
It is really difficult to apply our complex formulas for fast mental calculation because we must pay the price for their high accuracy. In the future, we will embed these formulas into software or hardware of medical ultrasound machine so that users are easy to read estimated values resulted from the machine. The research is available at http:// phoebe.locnguyen.net so that doctors and researchers are easy to use. We do not know whether they have enjoyed our product. However, we have presented Phoebe framework at Ho Chi Minh City Society of Reproductive Medicine (HOSREM) on November 26, 2016 and so many doctors knew and concerned it.
Within the context of this research, from section of 3-dimension ultrasound in PhD dissertation of the author Ho [5], I recognize that fetus weight and fetus age are mutually dependent. For instance, when fetus age increases, fetus weight increase too. Therefore their estimation formulas should be implied together as follows:

Where f, g are normal regression functions of weight and age, respectively. The coefficients λ and μ are called dual coefficients.
These formulas represent a so-called dual regression model of fetus age and weight estimation. In the future, we will research such dual model in order to improve accuracy of estimate formulas with experimental viewpoint. This future trend is potential although it takes a lot of efforts to implement the dual model.
Acknowledgement
We express our deep gratitude to the author Michael Thomas Flanagan – University College London and the author Jos de Jong for giving us helpful software packages that help us to implement the framework.
References
- Nguyen L, Ho H (2014) A framework of fetal age and weight estimation. Journal of Gynecology and Obstetrics 2: 20-25.
- Hadlock FP, Harrist RB, Sharman RS, Deter RL, Park SK (1985) Estimation of fetal weight with use of head, body and femur measurements: A prospective study. Am J Obstet Gynecol 151: 333-337.
- Phan DT (1985) Ứng dụng siêu âm �?�? chẩn �?oán tu�?i thai và cân nặng thai trong tử cung. Hanoi University of Medicine, Hanoi.
- Phạm TT (2000) Ư�?c lượng cân nặng thai nhi qua các s�? �?o của thai trên siêu âm. Ho Chi Minh University of Medicine and Pharmacy. Ho Chi Minh.
- Ho TT (2011) Nghiên Cứu Phương Pháp Ư�?c Lượng Trọng Lượng Thai, Tu�?i Thai Bằng Siêu Âm Hai và Ba Chiều. Hanoi Univerisy of Medicine. Hanoi.
- Shepard JM, Richards AV, Berkowitz LR, Warsof LS, Hobbins CJ (1982) An evaluation of two equations for predicting fetal weight by ultrasound. Am J Obstet Gynecol 142: 47-54.
- Campbell S, Wilkin D (1975) Ultrasonic measurement of fetal abdomen circumference in the estimation of fetal weight. An International Journal of Obstetrics and Gynaecology 82: 689-697.
- Lee W, Balasubramaniam M, Deter RL, Yeo L, Hassan SS, et al. (2009) New fetal weight estimation models using fractional limb volume. Ultrasound Obstet Gynecol 34: 556-565.
- Chang FM, Liang RI, Ko HC, Yao BL, Chang CH, et al. (1997) Three-dimensional ultrasound-assessed fetal thigh volumetry in predicting birth weight. Obstet Gynecol 90: 331-339.
- Varol F, Saltik A, Kaplan PB, Kiliç T, Yardim T (2001) Evaluation of gestational age based on ultrasound fetal growth measurements. Yonsei Med J 42: 299-303.
- Flanagan MT (2004) Michael Thomas Flanagan's Java Scientific Library. University College, London.
- Jong Jd (2010) A Java expression parser. A Java expression parser. Rotterdam, SpeQ Mathematics: Netherlands.
- Oracle (2014) Java language.
- Ho TT, Phan DT (2011) Ư�?c lượng cân nặng của thai từ 37 – 42 tuần bằng siêu âm 2 chiều. Journal of Practical Medicine 12: 8-9.
- Ho THT, Phan DT (2011) Ư�?c lượng tu�?i thai qua các s�? �?o th�? tích cánh tay bằng siêu âm 3 chiều và các s�? �?o bằng siêu âm 2 chiều. Journal of Practical Medicine 12: 12-15.
Relevant Topics
- Chronic Disease Management
- Community Based Nursing
- Community Health Assessment
- Community Health Nursing Care
- Community Nursing
- Community Nursing Care
- Community Nursing Diagnosis
- Community Nursing Intervention
- Core Functions Of Public Health Nursing
- Epidemiology
- Epidemiology in community nursing
- Health education
- Health Equity
- Health Promotion
- History Of Public Health Nursing
- Nursing Public Health
- Public Health Nursing
- Risk Factors And Burnout And Public Health Nursing
- Risk Factors and Burnout and Public Health Nursing
Recommended Journals
- Epidemiology journal
- Global Journal of Nursing & Forensic Studies
- Global Nursing & Forensic Studies Journal
- global journal of nursing & forensic studies
- journal of community medicine& health education
- journal of community medicine& health education
- Palliative Care & Medicine journal
- journal of pregnancy and child health
Article Tools
Article Usage
- Total views: 3394
- [From(publication date):
May-2017 - Aug 18, 2025] - Breakdown by view type
- HTML page views : 2492
- PDF downloads : 902
