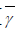Research Article Open Access
Hard Decision Based Cooperative Spectrum Sensing over Different Fading Channel in Cognitive Radio
Md. Shamim Hossain1*,Sharif Mohammed Babul Haque2,Md. Ibrahim Abdullah3 and Mohammad Alamgir Hossain41Lecturer, Dept. of CSE, Islamic University, Kushtia, Bangladesh.
2Assistant Registrar, Atish Dipankar University of Science & Technology, Dhaka, Bangladesh.
3Associate Professor, Dept. of CSE, Islamic University, Kushtia, Bangladesh.
4Lecturer, Dept. of CSE, Atish Dipankar University of Science & Technology, Dhaka, Bangladesh.
- *Corresponding Author:
- Md. Shamim Hossain
Lecturer, Dept. of CSE, Islamic University, Kushtia, Bangladesh.
E-mail: shamimmalitha@yahoo.com
Visit for more related articles at International Journal of Advance Innovations, Thoughts & Ideas
Abstract
Spectrum sensing is the key component of cognitive radio technology. However, detection is compromised when a user experiences shadowing or fading effects. In such cases, user cannot distinguish between an unused band and a deep fade. Thus, cooperative spectrum sensing is proposed to optimize the sensing performance. We focus performance of cooperative CR user based on spectrum sensing using energy detector in non-fading channel AWGN and fading channels such as Rayleigh, Ricean and Nakagami. This paper presents a simulation comparison of these fading channels based on hard decision combining fusion rule (OR-rule, AND-rule and MAJORITY-rule). Fusion rule is performed at fusion center (FC) to make the final decision about the presence of PU. We observe that spectrum sensing is harder in presence of Rayleigh and Nakagami fading and performance of energy detection degrades more in Nakagami channels than Rayleigh and Ricean channels. It also found that Spectrum sensing in Ricean fading has better results than others.
Keywords
Cognitive Radio, Hard decision fusion rules, Cooperative spectrum sensing, fading channels, Energy detection
Introduction
Cognitive radio (CR) technique has been proposed to solve the conflicts between spectrum scarcity and spectrum under-utilization [1]. It allows the CR users to share the spectrum with primary users (PU) by opportunistic accessing. The CR can use the spectrum only when it does not cause interference to the primary users. Therefore, spectrum sensing is a critical issue of cognitive radio technology since it needs to detect the presence of primary users accurately and swiftly. Existing spectrum sensing techniques can be divided into three types [2]: energy detection, matched filter detection and cyclostationary detection. Among them, energy detection has been widely applied since it does not require any a priori knowledge of primary signals and has much lower complexity than the other two schemes. Spectrum sensing is a tough task because of shadowing, fading, and time-varying nature of wireless channels [2]. The radio channel is characterized by two types of fading effects: large scale fading and small scale fading [3], [4]. Small scale fading models include the wellknown Rayleigh, Rice, and Nakagami-m [5]-[6] distributions. For large scale fading conditions, it is widely accepted that the probability density function (PDF) of the fading envelopes can be modeled by the wellknown Log-normal distribution [7], [8]. Due to the several multipath fading, a cognitive radio may fail to notice the presence of the PU and then will access the licensed channel and cause interference to the PU. To combat these impacts, cooperative spectrum sensing schemes have been proposed to obtain the spatial diversity in multiuser CR networks [9-11]. The performance of single CR user based spectrum sensing in fading channels such as Rayleigh, Nakagami, Weibull has been studied in [12]. The performance of cooperative spectrum sensing with censoring of cognitive radios in Rayleigh fading channel has been evaluated in [13-15]. Cooperative spectrum sensing improves the detection performance. All CR users sense the PU individually and send their sensing information in the form of 1-bit binary decisions (1 or 0) to Fusion center (FC). The hard decision combining rule (OR, AND, and MAJORITY rule) is performed at FC using a counting rule to make the final decision regarding whether the primary user present or not [16]-[18]. Hard decision combination-based cooperative spectrum sensing has been addressed in [19-22]. However, the existed works only examined the additive white Gaussian noise (AWGN) channel and the Rayleigh fading channel. In this paper, we study hard decision based cooperative spectrum sensing over Rayleigh, Nakagami and Ricean fading channels.
The rest of this paper is organized as follows. In Section II, the system model is introduced. In Section III, detection and false alarm probabilities of non-fading AWGN and fading channel such as Rayleigh, Ricean and Nakagami are described. Cooperative spectrum sensing over various fading channels is derived in Section IV. The simulation result and discussion are presented in section V. Finally, we draw our conclusions in Section VI.
System Model
The local spectrum sensing is to decide between the following two hypotheses,
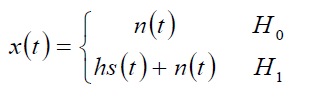 (1)
(1)
where x(t) is the signal received by secondary user and s(t) is primary user’s transmitted signal, n(t) is the additive white Gaussian noise (AWGN) and h is the amplitude gain of the channel. The energy collected in the frequency domain is denoted by Y which serves as a decision statistic. Following the work of Urkowitz [23], Y may be shown to have the following distribution,
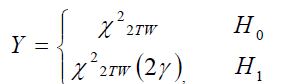 (2)
(2)
where and denote central and non-central chi-square distributions respectively, each with 2TW degrees of freedom and a non-centrality parameter of 2γ for the latter distribution. For simplicity we assume that time-bandwidth product, TW, is an integer number which we denote by u.
Detection and False Alarm Probabilities
In this section, we give the average detection probability over Rayleigh, Nakagami, and Ricean fading channels and in closed form [24]. In communications theory, Nakagami distributions, Rician distributions, and Rayleigh distributions are used to model scattered signals that reach a receiver by multiple paths. Depending on the density of the scatter, the signal will display different fading characteristics. Rayleigh and Nakagami distributions are used to model dense scatters, while Rician distributions model fading with a stronger line-of-sight. Nakagami distributions can be reduced to Rayleigh distributions, but give more control over the extent of the fading.
Non-fading environment (AWGN channel )
In non-fading environment the average probability of false alarm, the average probability of detection, and the average probability of missed detection are given, respectively, by [24]
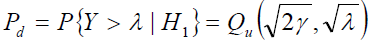 (3)
(3)
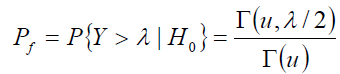 (4)
(4)
and
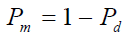 (5)
(5)
where λ denotes the energy threshold. Γ(.) and Γ(.,.) are complete and incomplete gamma functions respectively [25] and (.,.) Qu is the generalized Marcum Q-function defined as follows,
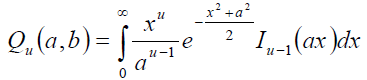
where 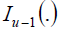 is the modified Bessel function of (u−1)th order. If the signal power is unknown, we can
first set the false alarm probability Pf to a specific constant. By equation (4), the detection threshold λ can be determined. Then, for the fixed number of samples 2TW the detection probability Pd can be evaluated by substituting the λ in (3). As expected, Pf is independent of γ since under
H0 there is no primary signal present. When h is varying due to fading, equation (3) gives the probability of detection as a function of the instantaneous SNR, γ. In this case, the average probability of detection
is the modified Bessel function of (u−1)th order. If the signal power is unknown, we can
first set the false alarm probability Pf to a specific constant. By equation (4), the detection threshold λ can be determined. Then, for the fixed number of samples 2TW the detection probability Pd can be evaluated by substituting the λ in (3). As expected, Pf is independent of γ since under
H0 there is no primary signal present. When h is varying due to fading, equation (3) gives the probability of detection as a function of the instantaneous SNR, γ. In this case, the average probability of detection 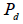 may be derived by averaging (3) over fading statistics [19],
may be derived by averaging (3) over fading statistics [19],
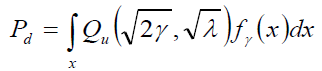 (6)
(6)
where fγ(x) is the probability distribution function (PDF) of SNR under fading.
Rayleigh fading channel
When the composite received signal consists of a large number of plane waves, for some types of scattering environments, the received signal has a Rayleigh distribution [26]. If the signal amplitude follows a Rayleigh distribution, then the SNR γ follows an exponential PDF given by
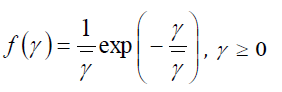 (7)
(7)
In this case, a closed-form formula for d P may be obtained (after some manipulation) by substituting  in (6),
in (6),
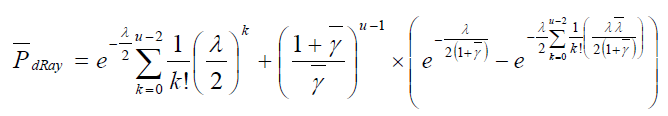 (8)
(8)
Ricean fading channel
Some types of scattering environments have a specular or LoS (Line of Sight) component. In this case, the amplitude of received signals has a Ricean distribution. If the signal strength follows a Rician distribution, the PDF of γ will be
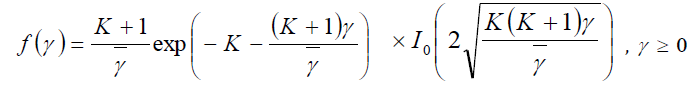 (9)
(9)
where K is the Rician factor. The average Pd in the case of a Rician channel, 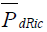 is then obtained by averaging (3) over (9) and substituting x for
is then obtained by averaging (3) over (9) and substituting x for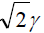 The resulting expression can be solved for u = 1 using [24], Eq. (45)] to yield
The resulting expression can be solved for u = 1 using [24], Eq. (45)] to yield
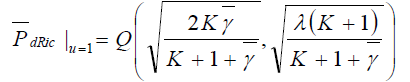 (10)
(10)
For K = 0, this expression reduces to the Rayleigh expression with u = 1.
Nakagami fading channel
Although Rayleigh and Ricean distributions are the most popular distributions to model fading channels, some experimental data does not fit well into neither of these distributions. Thus, a more general fading distribution was developed whose parameters can be adjusted to fit a variety of empirical measurements [25]. This distribution is called the Nakagami fading distribution. The Nakagami distribution was introduced by Nakagami in the early 1940’s to characterize rapid fading in long distance HF channels [27]. It is possible to describe both Rayleigh and Rician fading with the help of a single model using the Nakagami distribution. The Nakagami m-distribution is used in communication systems characterize the statistics of signal transmitted through multipath fading channels.
The Nakagami distribution is often used for the following reasons. First, the Nakagami distribution can model fading conditions that are either more or less severe than Rayleigh fading. When m=1, the Nakagami distribution becomes the Rayleigh distribution, when m=1/2, it becomes a one-sided Gaussian distribution, and when m=∞ the distribution becomes an impulse (no fading). Second, the Rice distribution can be closely approximated by using the following relation between the Rice factor K and the Nakagami shape factor m [27];
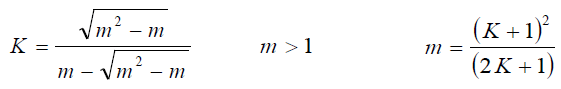
Since the Rice distribution contains a Bessel function while the Nakagami distribution does not, the Nakagami distribution often leads to convenient closed form analytical expressions that are otherwise unattainable. Using the alternative representation of Marcum-Q function given in [28, eq. (4.74), pp. 104], (1) can be written as,
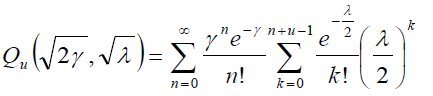 (11)
(11)
If the signal amplitude follows a Nakagami distribution, then the PDF of γ follows a gamma PDF given by
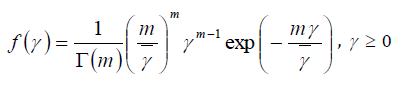 (12)
(12)
where m is the Nakagami parameter. The average Pd in the case of Nakagami channels  can now
be obtained by averaging (3) over (12) and then using again the change of variable
can now
be obtained by averaging (3) over (12) and then using again the change of variable 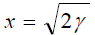 yielding
yielding
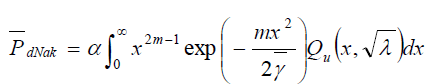 (13)
(13)
where
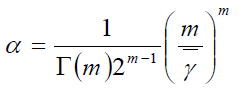 (14)
(14)
In this case, a closed-form formula of Nakagami channels can be given by
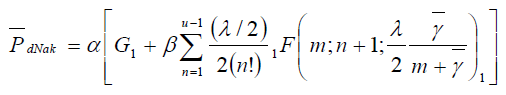 (15)
(15)
where 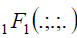 is the confluent hypergeometric function [18].
is the confluent hypergeometric function [18].
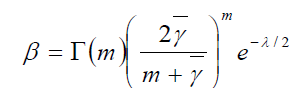 (16)
(16)
and
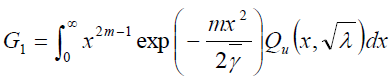 (17)
(17)
Where 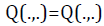 is the first-order Marcum Q-function. G1 can be evaluated for inter m with the aid of [25, Eq.(25)]
is the first-order Marcum Q-function. G1 can be evaluated for inter m with the aid of [25, Eq.(25)]
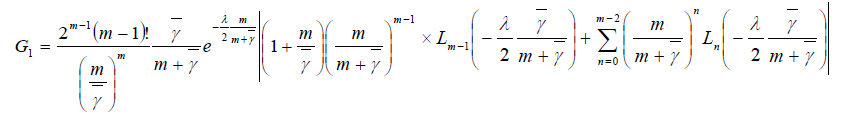 (18)
(18)
where is the Laguerre polynomial of degree n [25, 8.970].
Cooperative Spectrum Sensing over various Fading Channels
In real communication environments, the hidden terminal problem, deep fading and shadowing, etc., would deteriorate the signal detection performance of cognitive users. To address this issue, multiple cognitive radios can be coordinated to perform spectrum sensing. Several recent works have shown that cooperative spectrum sensing can greatly increase the probability of detection in fading channels [19], [29].
Let N denote the number of users sensing the PU. Each CR user makes its own decision regarding whether the primary user present or not, and forwards the binary decision (1 or 0) to fusion center (FC) for data fusion. The PU is located far away from all CRs. All the CR users receive the primary signal with same local mean signal power, i.e. all CRs form a cluster with distance between any two CRs negligible compared to the distance from the PU to a CR. For simplicity we have assumed that the noise, fading statistics and average SNR are the same for each CR user. We consider that the channels between CRs and FC are ideal channels (noiseless). Assuming independent decisions, the fusion problem where k out of N CR users are needed for decision can be described by binomial distribution based on Bernoulli trials where each trial represents the decision process of each CR user. With a hard decision counting rule, the fusion center implements an n–outof- M rule that decides on the signal present hypothesis whenever at least k out of the N CR user decisions indicate . Assuming uncorrelated decisions, the probability of detection at the fusion center [30] is given by
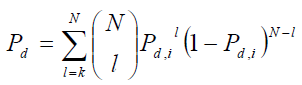 (19)
(19)
where Pd,i is the probability of detection for each individual CR user as defined by (3) and (6).
Logical AND-Rule
In this rule, if all of the local decisions sent to the decision maker are one, the final decision made by the decision maker is one. The fusion center’s decision is calculated by logic AND of the received hard decision statistics. Cooperative detection performance with this fusion rule can be evaluated by setting k=N in eq. (19).
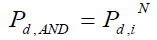 (20)
(20)
Logical OR-Rule
In this rule, if any one of the local decisions sent to the decision maker is a logical one, the final decision made by the decision maker is one. Cooperative detection performance with this fusion rule can be evaluated by setting k=1 in eq. (19).
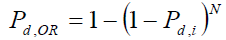 (21)
(21)
Logical MAJORITY -Rule
In this rule, if half or more of the local decisions sent to the decision maker are the final decision made by the decision maker is one. Cooperative detection performance with this fusion rule can be evaluated by setting k = N/2 in eq. (19).
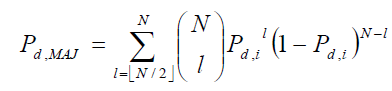 (22)
(22)
where 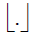 represents the floor operator.
represents the floor operator.
Experimental Results
All simulation was done on MATLAB version R2011a over three different fading under Rayleigh, Ricean and Nakagami channel and a non-fading channel AWGN. We described the receiver through its complementary ROC curves for different values of probability of false alarm and Cognitive Radio user.
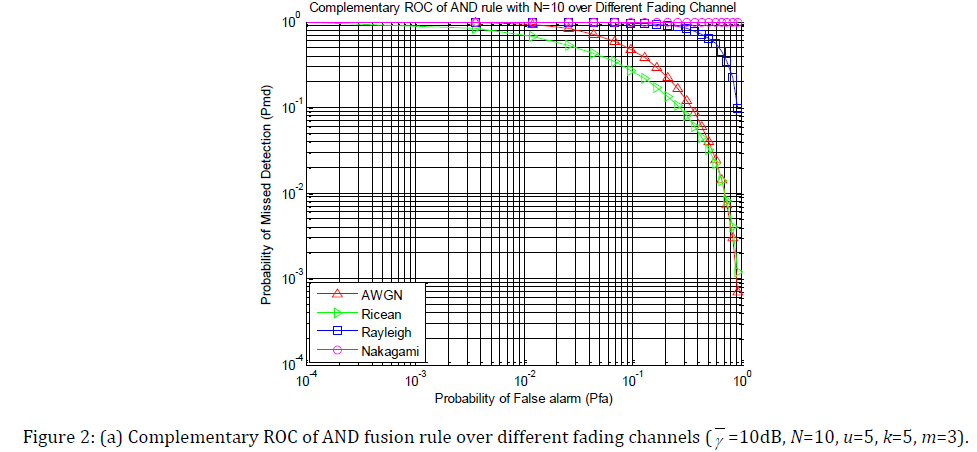
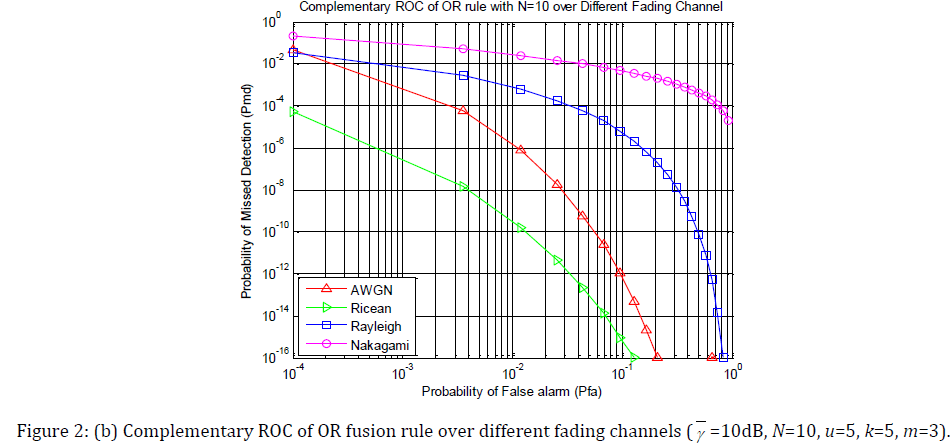
Fig. 2(a), 2(b) and 2(c) show complementary ROC curves of the 10 user’s spectrum sensing in three different fading under Rayleigh, Ricean and Nakagami fading following AND rule, OR rule and MAJORITY rule respectively. Average SNR and u are assumed to be 10 dB and 5 respectively. Rice factor k and Nakagami parameter m are set to be 5 and 3 respectively. A plot for non-fading (pure AWGN) case is also provided for comparison.
Comparing the AWGN curve with those corresponding to fading, we observe that spectrum sensing is harder in presence of Rayleigh and Nakagami fading. In Ricean channel, because of the LoS signal, the sensing performance is better than in other channels. We observe that the OR rule has the better performance than AND and MAJORITY rule in various channels.
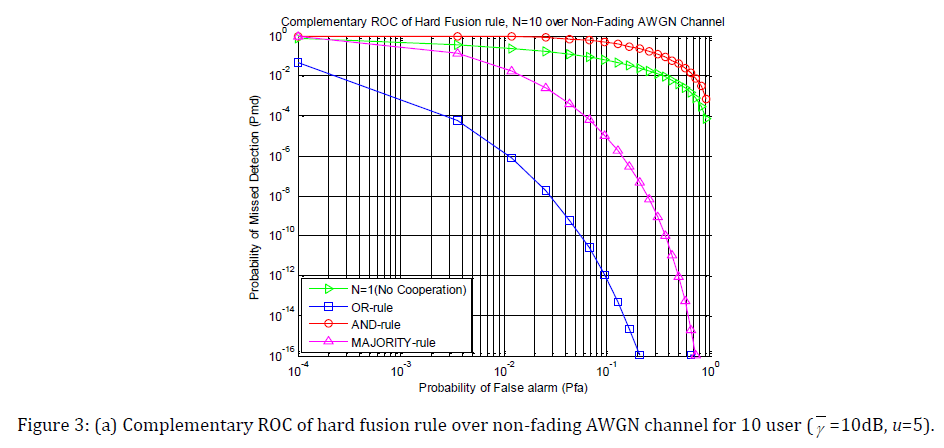
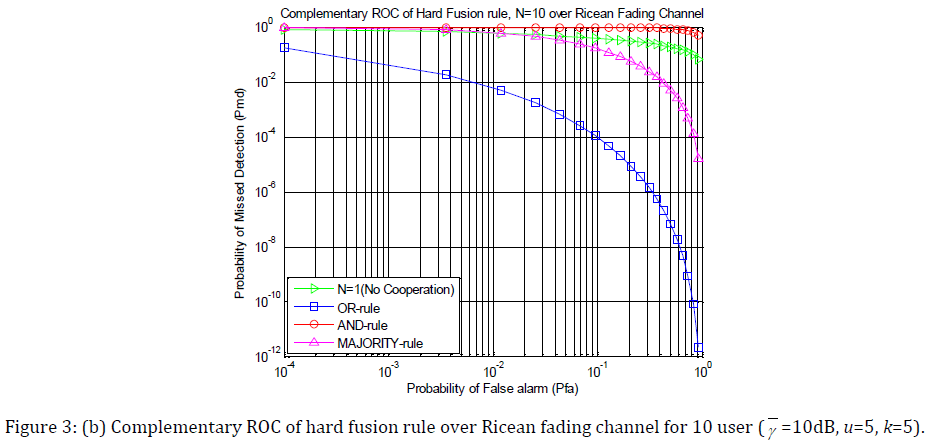
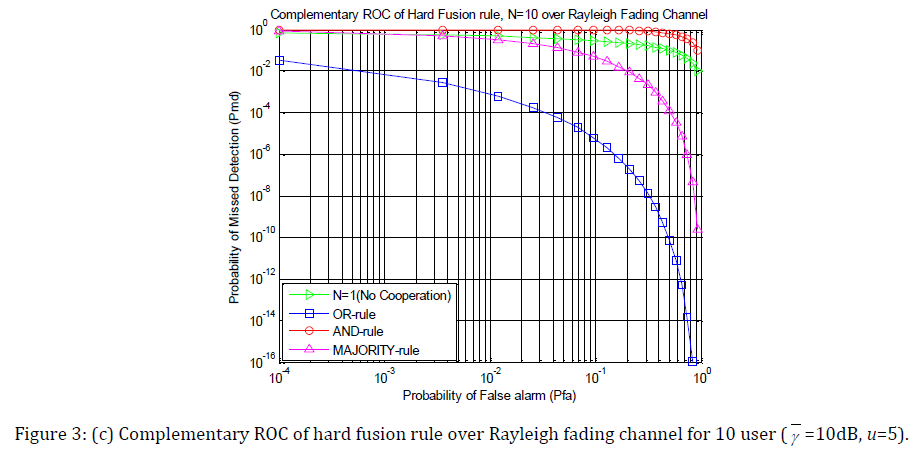
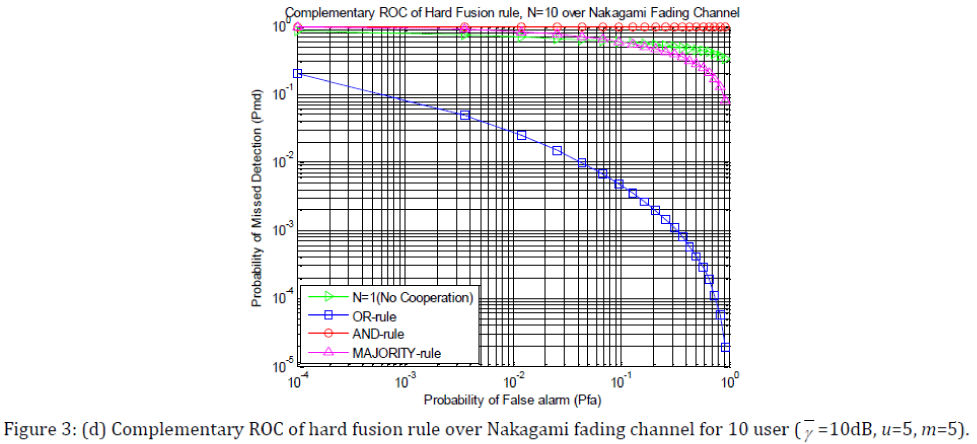
Fig. 3(a), 3(b), 3(c) and 3(d) show complementary ROC of hard decision fusion rule(AND-rule, OR-rule and MAJORITY-rule) of 10 user’s spectrum sensing in non-fading AWGN and three different fading under Rayleigh, Ricean and Nakagami fading respectively. A plot for single user’s spectrum sensing is also provided for comparison. As before γ = 10 dB, u =5, k = 5, m = 3.
Simulation result shows that probability of missed detection of AND rule is larger than missed detection of single user over various channels. It also shows that OR rule has the better performance than AND and MAJORITY rule. Comparing the AWGN curve with those corresponding to fading, we observe that spectrum sensing is harder in presence of Rayleigh and Nakagami fading.
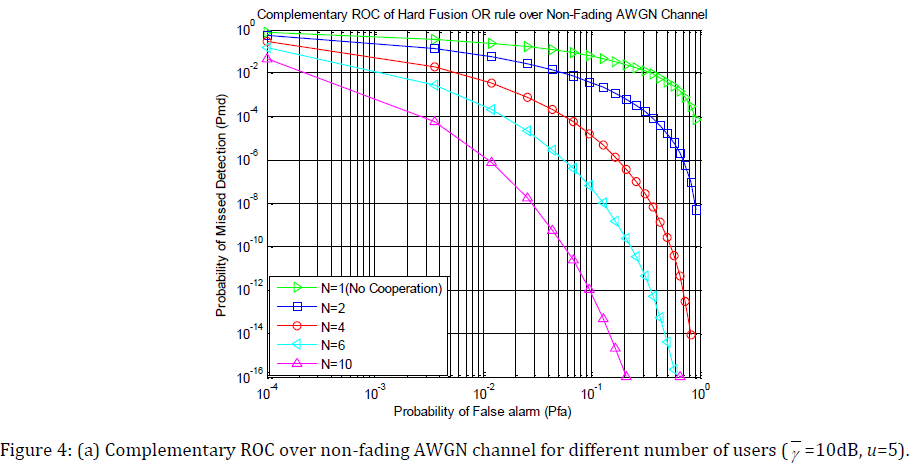
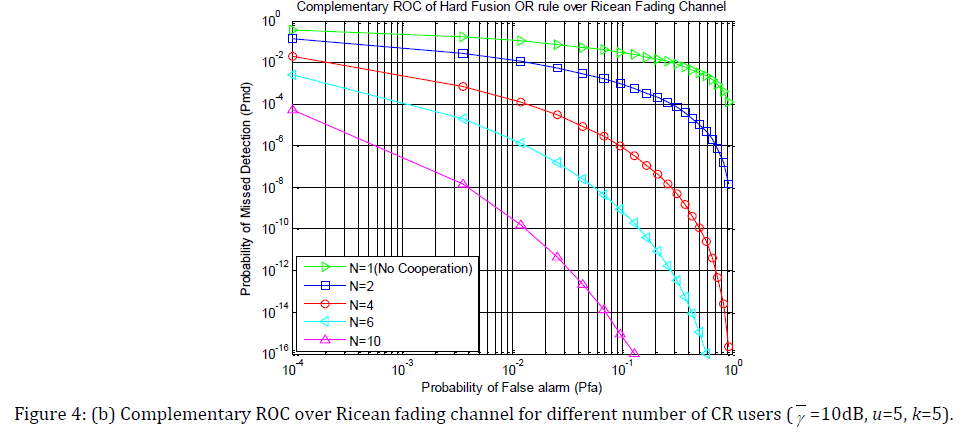
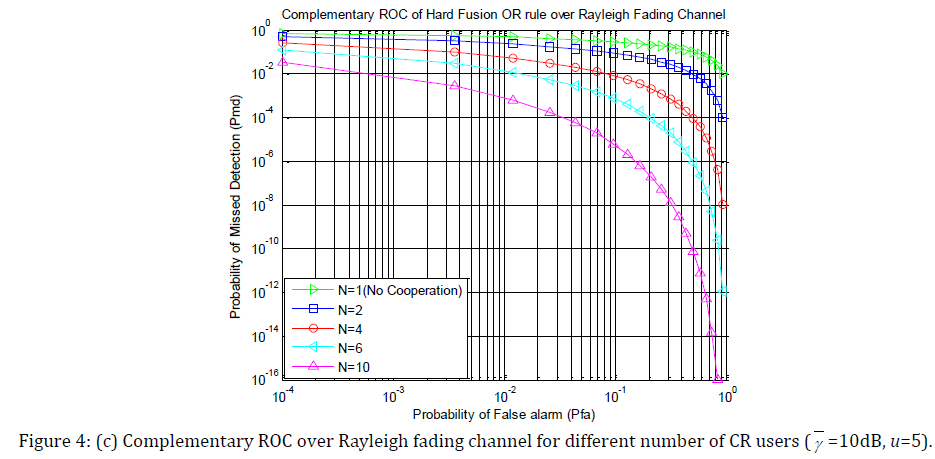
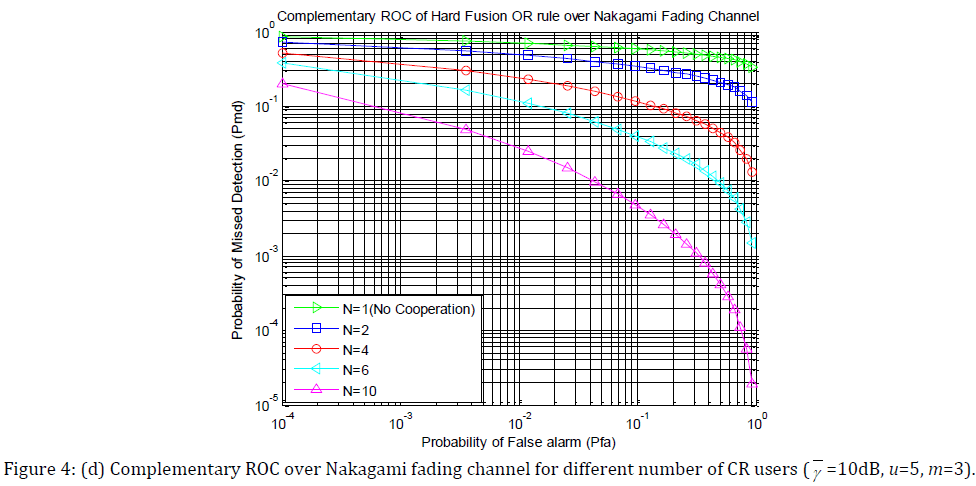
Fig. 4(a), 4(b), 4(c) and 4(d) show the complementary ROC of hard decision fusion OR rule for different number of cooperative users of cooperative spectrum sensing over non-fading AWGN channel and three different fading such as Ricean, Rayleigh and Nakagami fading channel respectively. A plot for single user’s spectrum sensing is also provided for comparison. As before γ = 10 dB, u =5, k = 5, m = 3.
Simulation result shows that cooperative sensing performance is getting better with increasing CR user as for larger CR user, with high probability there will be a user with a preferable channel to find the presence of PU.
Conclusion & Future Work
We have studied hard decision based cooperative spectrum sensing over different fading channel in cognitive radio. Performance of cooperative spectrum sensing over Rayleigh, Ricean and Nakagami fading are presented and compared. It has been found that probability of missed detection is decreased by using different hard decision fusion rules. We observe that the OR rule has the better performance than AND and MAJORITY rule in various channels. We also observe that spectrum sensing is harder in presence of Rayleigh and Nakagami fading and performance of energy detection degrades more in Nakagami channels than Rayleigh and Ricean channels. In Ricean channel, because of the LoS signal, the sensing performance is better than in other channels. Furthermore, spectrum sensing in Ricean fading has better results than others.
References
- S. Haykin, “Cognitive radio: brain-empowered wireless communications,” IEEE Journal on Selected Areas in Communications, vol. 23, no. 2, pp. 201-220, Feb. 2005.
- D. Cabric, S. M. Mishra, and R. W. Brodersen, “Implementation issues in spectrum sensing for cognitive radios,” in Proc. Asilomar Conf. on Signals, Systems, and Computers, Nov. 7-10, 2004, vol. 1, pp. 772–
- B. Sklar, “Rayleigh fading channels in mobile digital communication systems, Part I: Characterization”, IEEE Communications Magazine, 1997, vol. 35, no. 7, p. 90 - 100.
- H. Suzuk, “A statistical model for urban radio propagation”, IEEE Transactions on Communications, 1977, vol. COM-25, no. 7, p. 673 to 680.
- M. K. Simon and M.-S. Alouini, Digital Communication over Fading Channels, 2nd edition. New York: Wiley, 2004.
- N. C. Sagias, G. K. Karagiannidis, D. A. Zogas, P. T. Mathiopoulos, and G. S. Tombras, "Performance analysis of dual selection diversity in correlated Weibull fading channels," IEEE Trans. Commun., vol. 52, no.
- G. L. Turin, F. D. Clapp, T. L. Johnston, S. B. Fine, and D. Lavry, "A statistical model of urban multipath propagation," IEEE Trans. Veh. Technol., vol. VT-21, p. 19, Feb. 1972.
- F. Hansen and F. I. Meno, "Mobile fading-Rayleigh and Lognormal superimposed," IEEE Trans. Veh. Technol., vol. VT-26, pp. 332-335, Nov. 1977.
- G. Ganesan and Y. (G.) Li, “Cooperative spectrum sensing in cognitive radio–part I: two user networks,” IEEE Trans. Wireless Commun., vol. 6, no. 6, pp. 2204–2213, June 2007.
- G. Ganesan and Y. (G.) Li, “Cooperative spectrum sensing in cognitive radio part II: multiuser networks,” IEEE Trans. Wireless Commun., vol. 6, no. 6, pp. 2214–2222, June 2007.
- S. M. Mishra, A. Sahai, and R. W. Brodersen, “Cooperative sensing among cognitive radios,” in Proc. IEEE Int. Conf. on Commun. June, 2006, vol. 4, pp. 1658–1663.
- S. Nallagonda, S. Suraparaju, S. D. Roy and S. Kundu, “Performance of energy detection based spectrum sensing in fading channels”, in Proc. of IEEE International Conference on Computer and
- S. Nallagonda, S. D. Roy and S. Kundu, “Performance of cooperative spectrum sensing with censoring of cognitive Radios in Rayleigh Fading Channel”, in Proc. of IEEE INDICON 2011, December.
- S. Nallagonda, S. D. Roy and S. Kundu, “Cooperative spectrum sensing with censoring of cognitive Radios in Rayleigh Fading Channel”, accepted in Proc. of IEEE Eighteenth National conference on
- S. Nallagonda, S.D Roy and S. Kundu, “Performance of Cooperative Spectrum Sensing in Log-normal Shadowing and Fading under Fusion Rules”, Int. Jour. Of Enery. Infor. And Comm. pp. 15-28, Vol. 3, Aug. 2012.
- A. Ghasemi and E. S. Sousa, “Opportunistic spectrum access in fading channels through collaborative sensing,” IEEE Journal on selected Areas in Communications, vol. 2, no. 2, pp. 71-82, March, 2007.
- A. Ghasemi and E. S. Sousa, “Impact of user collaboration on the performance of opportunistic spectrum access,” in Proc. IEEE Vehicular Technology Conference (VTC Fall'06), Montreal, September 2006.
- A. Ghasemi and E. S. Sousa, “Collaborative spectrum sensing for opportunistic access in fading
- S. H Lee, Y. H. Lee, S, “Hard Decision Combining-based Cooperative Spectrum Sensing in Cognitive Radio Systems”.
- S. Kyperountas, N. Correal and Q. Shi, “A comparison of Fusion Rules for Cooperative Spectrum Sensing in Fading Channels”, EMS Research, Motorola.
- L. Jiajun, T. Zhenhui, Ai Bo and Y. Shan, “Weighted Hard combination for cooperative Spectrum Sensing in Cognitive Radio Networks”, Research paper, pp.111-116, March, 2011.
- N. Armi, N.M. Saad and M. Arshad, “Hard Decision Fusion based Cooperative Spectrum Sensing in Cognitive Radio System”, ITB, vol.3, No.2, 2009, pp. 109-122.
- H. Urkowitz, “Energy detection of unknown deterministic signals,” Proc. IEEE, vol. 55, pp. 523–531, Apr. 1967.
- F. F. Digham, M.-S. Alouini and M. K. Simon, “On the energy detection of unknown signals over fading channels,” in Proc. of IEEE International Conference on Communications (ICC’03), pp. 3575–3579, May 2003.
- I. S. Gradshteyn and I. M. Ryzhik, Table of Integrals, Series, and Products, 7th ed. Academic Press, 2007.
- G. L. Stuber, Principles of Mobile Communications, second ed. Norwell, MA: Kluwer Academic Publishers, 2002.
- M. Nakagami, “The m distribution; a general formula of intensity distribution of rapid fading,” Statistical Methods in Radio Wave Propagation, W.G. Hoffman, ed., pp. 3–36, 1960.
- A. H. Nuttall, “Some integrals involving the QM-function,” Naval Underwater Systems Center (NUSC) technical report, May 1974.
- G. Ganesan and Y. Li, “Cooperative spectrum sensing in cognitive radio networks,” in Proc. DySPAN, Nov. 2005, pp. 137-143.
- Spyros Kyperountas, Neiyer Correal, Qicai Shi and Zhuan Ye, “Performance analysis of cooperative spectrum sensing in Suzuki fading channels,” in Proc. of IEEE International Conference on Cognitive Radio
Relevant Topics
- Advance Techniques in cancer treatments
- Advanced Techniques in Rehabilitation
- Artificial Intelligence
- Blockchain Technology
- Diabetes care
- Digital Transformation
- Innovations & Tends in Pharma
- Innovations in Diagnosis & Treatment
- Innovations in Immunology
- Innovations in Neuroscience
- Innovations in ophthalmology
- Life Science and Brain research
- Machine Learning
- New inventions & Patents
- Quantum Computing
Recommended Journals
Article Tools
Article Usage
- Total views: 15838
- [From(publication date):
May-2013 - Sep 04, 2025] - Breakdown by view type
- HTML page views : 11064
- PDF downloads : 4774