Research Article Open Access
Image Enhancement by Wavelet with Principal Component Analysis
Vikas D .Patil*, Sachin D RuikarDepartment of Electronics & Telecommunication Dept., Sinhgad Academy of Engg, Pune, India
- *Corresponding Author:
- Vikas D .Patil
Department of Electronics & Telecommunication Dept
Sinhgad Academy of Engg, Pune, India
E-mail:vikaspatils@gmail.com
Visit for more related articles at International Journal of Advance Innovations, Thoughts & Ideas
Abstract
This paper demonstrate the dimensionality of image sets with Wavelet using principal component analysis on wavelet coefficients to maximize edge energy in the reduced dimension images. Large image sets, for a better preservation of image local structures, a pixel and its nearest neighbors are modeled as a vector variable, whose training samples are selected from the local window by Local Pixel Grouping (LPG).
The LPG algorithm guarantees that only the sample blocks with similar contents are used in the local statistics calculation for PCA transform estimation, so that the image local features can be well preserved after coefficient shrinkage in the PCA domain to remove the random noise. The LPG-PCA Enhance procedure is used to improve the image quality.
The wavelet thresholding methods used for removing random noise has been researched extensively due to its effectiveness and simplicity. However, not much has been done to make the threshold values adaptive to the spatially changing statistics of images. Such adaptivity can improve the wavelet thresholding performance because it allows additional local information of the image (such as the identification of smooth or edge regions) to be incorporated into the algorithm of a damaged or target region in addition to shape and texture properties
Keywords
Wavelet, Wavelet Transform (WT), Local Pixel Grouping (LPG), Principal Components Analysis (PCA).
Introduction
Principal Components Analysis (PCA) is the way of identifying patterns in data, and expressing the data in such a way as to highlight their similarities and differences. Since patterns in data can be hard to find in data of high dimension, where the luxury of graphical representation is not available PCA is a powerful tool for analyzing data. The other main advantage of PCA is that once you have found these patterns in the data and you compress the data i.e. by reducing the number of dimensions without much loss of information. This technique used in image compression. To improve the image quality image enhancement is an essential step. As a primary low-level image processing procedure, random noise removal has been extensively studied and many enhancement schemes have been proposed, from the earlier smoothing filters and frequency domain denoising methods [1] to the lately developed wavelet [2][3][11], curvelet [12] and ridgelet [13] based methods, sparse representation [14].With the rapid development of modern digital imaging devices and their increasingly wide applications in our daily life, to overcome the problem with conventional WT [15] we use Wavelet PCA. Wavelets are an efficient and practical way to represent edges and image information at multiple spatial scales. Image features at a given scale, such as houses or roads, can be directly enhanced by filtering the wavelet coefficients. Wavelets may be a more useful image representation than pixels. Hence, we consider PCA dimensionality reduction of wavelet coefficients in order to maximize edge information in the reduced dimensionality set of images. The wavelet transform will take place spatially over each image band, while the PCA transform will take place spectrally over the set of images. Thus, the two transforms operate over different domains. Still, PCA over a complete set of wavelet and approximation coefficients will result in exactly the same eigenspectra as PCA over the pixels.
To overcome the problem of WT, in [16] Muresan and Parks proposed a spatially adaptive principal component analysis (PCA) based denoising scheme, which computes the locally fitted basis to transform the image. Elad and Aharon [14] [17] proposed sparse redundant representation and (clustering -singular value decomposition) K-SVD based denoising algorithm by training a highly over-complete dictionary. Foi et al. [18] applied a shape-adaptive discrete cosine transform (DCT) to the neighborhood, which can achieve very sparse representation of the image and hence lead to effective denoising. All these methods show better denoising performance than the conventional WT-based denoising algorithms. The recently developed non-local means (NLM) approaches use a very different philosophy from the above methods in random noise removal. The idea of NLM can be traced back to [19], where the similar image pixels are averaged according to their intensity distance. Similar ideas were used in the bilateral filtering methods [20] [21], where both the spatial and intensity similarities are exploited for pixel averaging. In [22], the NLM denoising frame- work was well established. Each pixel is estimated as the weighted average of all the pixels in the image, and the weights are determined by the similarity between the pixels. This scheme was improved in [23], where the pair-wise hypothesis testing was used in the NLM estimation. Inspired by the success of NLM methods, recently Dabov et al. [24] proposed a collaborative image denoising scheme by patch matching and sparse 3D transform. They searched for similar blocks in the image by using block matching and grouped those blocks into a 3D cube.
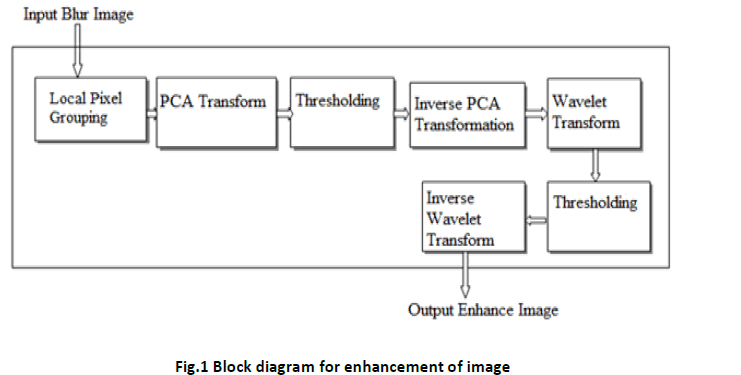
In the system we give an input as a blur image then apply algorithm Local Pixel Grouping then performs the principal component analysis (PCA) on the blur image. The output from PCA is the eigenimage and the eigenvectors. Apply soft thresholding on a PCA component, the number of them can be selected by the user, and the reconstruction quality in the inverse PCA (IPCA) depends on that number. The eigenimages and the eigenvectors are entropy coded. Then the wavelet transform (WT) is applied to that residual. Then apply thresholding on wavelet coefficient and the reconstruction quality in the Inverse Wavelet Transform (IWT). And finally get the output enhanced image. The rest of the paper is structured as follows. Section 2 briefly reviews the experimental results. Section 3 presents discussion of procedure of PCA, Wavelets transform , Implementation paper. Section 4 concludes the paper.
Experimental Results
In experimenting result, we try the different experiment to prove the superiority of proposed method. The experimental processes are conducted: it shows Enhancement images. We use the several different characteristic of the images, prove that our Local Pixel Grouping be used provides better results than other existing technique. In order to test the quality of our proposed image Enhancement method, we used various images, including photos, scenery, and artistic compositions. Also we have used different wavelet transforms.
Principle Component Analyses
Denote by x=[x1,x2 ,. . . xm]T an m-component vector variable and denote by
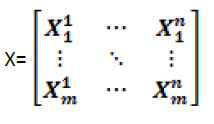 (1)
(1)
.the sample matrix of x, where xji , j=1,2,..,n, are the discrete samples of variable xi , i=1,2,..,m. The ith row of sample matrix X, denoted by
xi=[xi1,xi2 ,. . . xin] (2)
is called the sample vector of xi. The mean value of Xi is calculated as
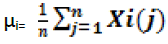 (3)
(3)
and then the sample vector Xi is centralized as
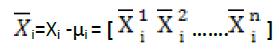 (4)
(4)
Where 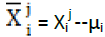 accordingly, the centralized matrix of X is
accordingly, the centralized matrix of X is
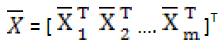 (5)
(5)
Finally, the co-variance matrix of the centralized dataset is calculated as
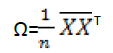 (6)
(6)
The goal of PCA is to find an ortho-normal transformation matrix P to de-correlate 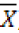 , i.e.
, i.e.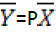 so that the covariance matrix of Y is diagonal. Since the covariance matrix X is symmetrical, it can be written as:
so that the covariance matrix of Y is diagonal. Since the covariance matrix X is symmetrical, it can be written as:
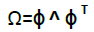 (7)
(7)
where ø = [ ø 1 ø 2 ……. ø n] is the m*m orthonormal eigenvector matrix and ^ = diag{λ1λ2..λm}is the diagonal eigenvalue matrix with λ1>= λ2 >=……….>=λm the terms ø1 ø2 ……. øn and the λ1,λ2..λm are the eigenvectors and eigenvalues of X. By setting
P= ø T (8)
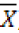 can be decorrelated.
can be decorrelated.
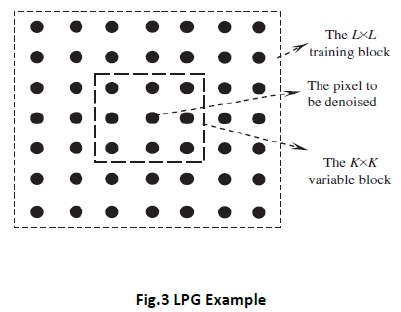
Local Pixel Grouping (LPG)
The LPG, for an under lying pixel to be denoised, we set a K*K window centered on it and denote by x=[x1………xm]T,m=K2,the vector containing all the components within the window. Since the observed image is noise corrupted, we denote by
Xv=X+v (9)
Grouping the training sample similar to the central K*K block in the L*L training window is indeed a classification problem and thus different grouping methods, such as block matching, correlation-based matching , K-mean s clustering, etc, can be employed based on different criteria. Among them the block matching method may be the simplest yet very efficient one. There are totally (L-K+1)2 possible training blocks of xn in the L*L training window. We denote by 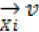 the column sample vector containing the pixel sin the central K*K block an denote by
the column sample vector containing the pixel sin the central K*K block an denote by 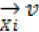 , i=1,2,…, (L-K+1)2-1,the sample vectors corresponding to the other blocks. Let
, i=1,2,…, (L-K+1)2-1,the sample vectors corresponding to the other blocks. Let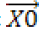 and
and 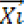 be the associated noise less sample vectors of
be the associated noise less sample vectors of 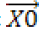 and
and 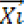 and, respectively. It can be easily calculated that
and, respectively. It can be easily calculated that
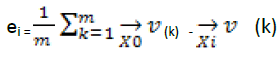 (10)
(10)
In above equation we used the fact that noise u is white and uncorrelated with signal. with equation if
 (11)
(11)
Where T is a preset threshold, then we select 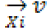 as a sample vector of Xv. Suppose we select n sample vectors of Xv including the central vector
as a sample vector of Xv. Suppose we select n sample vectors of Xv including the central vector 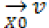 For the convenience of expression, we denote these sample vectors as
For the convenience of expression, we denote these sample vectors as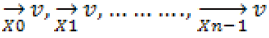 The noise less counter parts of these vectors are denoted as
The noise less counter parts of these vectors are denoted as
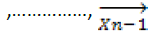 accordingly. The training dataset for xv is then formed by
accordingly. The training dataset for xv is then formed by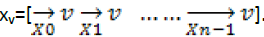 The noiseless counterpart of Xv is denoted as
The noiseless counterpart of Xv is denoted as 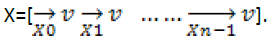
Wavelet
For the wavelet transform, the coefficients at the course level represent a larger time interval but a narrower band of frequencies. This feature of the wavelet transform is very important for image coding. In the active areas, the image data is more localized in the spatial domain, while in the smooth areas, the image data is more localized in the frequency domain. With traditional transform coding, it is very hard to reach a good compromise. The target region (damaged or lost data or object to be removed) information of the image can be divided into two kinds of conditions. The first class, the distribution of the target information of the image is the local and concentration.
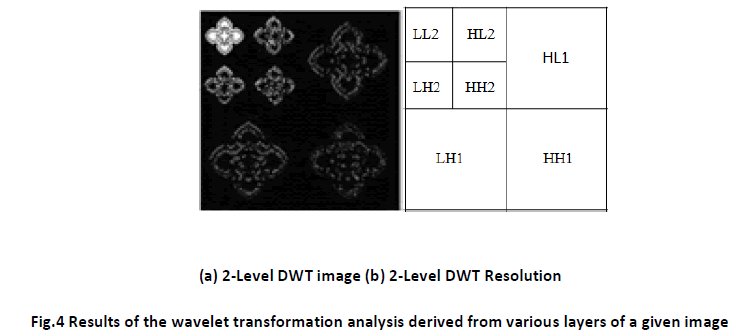
Wavelet transform has been used for various image analysis problems due to its nice multi-resolution properties and decoupling characteristics. The proposed algorithm utilizes the advantages of wavelet transforms for image Enhancement. Wavelet transform has been used as a good image representation and analysis tool mainly due to its multi-resolution analysis, data reparability, and compaction and sparsely features in addition to statistical properties [13]. A wavelet function (t) is a small wave, which must be oscillatory in some way to discriminate between different frequencies. The wavelet [5] [6] [10] contains both the analysing shape and the window. In order to observe the degree of influence of image textural on the reconstructed composition, we applied the two-level wavelet transformation to separate an image into three frequency components: high, medium, and low, as shown in Fig.3 (a).
The original image was processed through a secondary-level wavelet transformation analysis, as illustrated in Fig4 (a), where the highlighted image in the uppermost left hand corner is represented by the section LL2 illustrated in Fig.4 (b). Where analysis is concerned, the components of the overall image composition are all taken into consideration. This procedure can also be utilized as preliminary image analysis. The four components LL2, LH2, LH2, and HH2 are then processed through reversed wavelet transformations to heighten the resolution of the image.
Discrete Wavelet Transform
Filters are one of the most widely used signal processing functions. Wavelets [7][8][9] can be realized by iteration of filters with rescaling. The resolution of the signal, which is a measure of the amount of detail information in the signal, is determined by the filtering operations, and the scale is determined by up sampling and down sampling (sub sampling) operations [25].
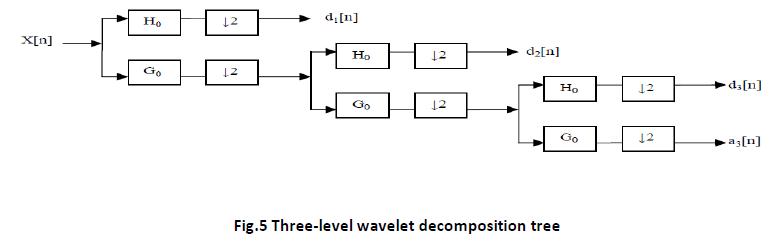
The DWT is computed by successive low pass and high pass filtering of the discrete time-domain signal as shown in figure 5. This is called the Mallat algorithm or Mallat-tree decomposition. Its significance is in the manner it connects the continuous time mutiresolution to discrete-time filters. In the figure, the signal is denoted by the sequence x[n], where n is an integer. The low pass filter is denoted by G0 while the high pass filter is denoted by H0. At each level, the high pass filter produces detail information d[n], while the low pass filter associated with scaling function produces coarse approximations, a[n].
A highest frequency of ω, which requires a sampling frequency of 2ω radians, then it now, has a highest frequency of ω/2 radians. It can now be sampled at a frequency of ω radians thus discarding half the samples with no loss of information. This decimation by 2 halves the time resolution as the entire signal is now represented by only half the number of samples. Thus, while the half band low pass filtering removes half of the frequencies and thus halves the resolution, the decimation by 2 doubles the scale.
Figure 6 shows the reconstruction of the original signal from the wavelet coefficients. Basically, the reconstruction is the reverse process of decomposition. The approximation and detail coefficients at every level are up sampled by two, passed through the low pass and high pass synthesis filters and then added. This process is continued through the same number of levels as in the decomposition process to obtain and H the original signal. The Mallat algorithm works equally well if the analysis filters, G0 and H0, are exchanged with the synthesis filters, G1 and H1.Then the filters have to satisfy the following two conditions as given in [26]:
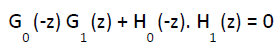 (12)
(12)
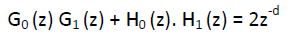 (13)
(13)
Implementation
Steps for the image enhancement by wavelet with PCA analysis are carried out as below.
I. Apply algorithm of LPG on input blur image.
II. Do the PCA transform of LPG output image as below.
a. Get some data.
b. Subtract the mean.
c. Calculate the covariance matrix.
d. Calculate the eigenvectors and eigenvalues of the covariance matrix.
e. Choosing components and forming a feature vector.
f. Deriving the new data set.
III. Apply the soft thresholding of PCA output image.
IV. Take Inverse PCA.
V. Do Wavelet transform of IPCA output image.
VI. Apply the soft thresholding of Wavelet output image.
VII. Take Inverse WT.
VIII. Calculate PSNR for the evaluation of the algorithm.
Conclusion
To preserve the local image structures when Enhancement, we modeled a pixel and its nearest neighbors as a vector variable, and the Enhancement of the pixel was converted into the estimation of the variable from its noisy observations. The PCA technique was used for such estimation and the PCA transformation matrix was adaptively trained from the local window of the image. However, in a local window there can have very different structures from the underlying one; therefore, a training sample selection procedure is necessary.
The block matching based local pixel grouping (LPG) was used for such a purpose and it guarantees that only the similar sample blocks to the given one are used in the PCA transform matrix estimation. The PCA transformation coefficients were then shrunk to remove noise.
References
- R.C.Gonzalez, R.E. Woods, Digital Image Processing, seconded., Prentice-Hall, EnglewoodCliffs,NJ,2002.
- D.L.Donoho, De-noising by soft thresholding, IEEE Transactions on Information Theory 41(1995)613–627.
- R.R.Coifman, D.L.Donoho,Translation-invariantde-noising,in:A.Antoniadis,G. Oppenheim (Eds.), Wavelet and Statistics,Springer,Berlin,Germany,1995.
- M.K.Mıhc-ak, I.Kozintsev, K. Ramchandran, P. Moulin ,Low complexity image denoising based on statistical modeling of wavelet coefficients, IEEE Signal Processing Letters6(12)(1999)300–303.
- S.G.Chang,B. Yu,M.Vetterli, Spatially adaptive wavelet thresholding with context modeling for image denoising ,IEEE Transaction on Image Processing 9 (9)(2000)1522–1531.
- A.Pizurica,W. Philips, I. Lamachieu, M. Acheroy, A jointinte and intra scale statistical model for Bayesian wavelet based image denoising, IEEE Transaction on Image Processing11(5)(2002)545–557.
- L.Zhang, B. Paul, X. Wu, Hybridinter and intra wavelet scale image restoration, Pattern Recognition 36(8)(2003)1737–1746.
- Z.Hou,Adaptive singular value decomposition in wavelet domain for image denoising, Pattern Recognition36(8)(2003)1747–1763.
- J.Portilla,V. Strela, M.J.Wainwright,E. P.Simoncelli, Image denoising using scale mixtures of Gaussians in the wavelet domain, IEEE Transaction on Image Processing 12(11)(2003)1338–1351.
- L.Zhang,P.Bao,X.Wu,MultiscaleLMMSE-based image denoising with optimal wavelet selection, IEEE Transaction on Circuits and Systems for Video Technology15(4)(2005)469–481.
- A.Pizurica,W.Philips, Estimating the probability of the presence a signal of interest in multire solution single and multi-image denoising, IEEE Transaction on Image Processing15(3)(2006)654–665.
- J.L.Starck,E.J.Candes,D.L.Donoho,The curvelet transform for image denoising, IEEE Transaction on Image Processing11(6)(2002)670–684.
- G.Y.Chen,B.Ke´gl, Image denoising with complex ridgelets, Pattern Recognition 40(2)(2007)578–585.
- M.Elad,M.Aharon, Image denoising viasparse and redundant representations over learn eddiction aries, IEEE Transaction on Image Processing15(12) (2006)3736–3745.
- S . Mallat, A Wavelet Tour of Signal Processing, Academic Press, New York, 1998.
- D.D.Muresan,T.W.Parks, Adaptive principal components and image denoising, in: Proceedings of the 2003 International Conference on Image Processing,14–17September,vol.1,2003,pp.I101–I104.
- M.Aharon,M.Elad,A.M.Bruckstein,The K-SVD: an algorithm for designing of over complete diction arise for sparse representation, IEEE Transaction on Signal Processing54(11)(2006)4311–4322.
- A.Foi, V.Katkovnik, K.Egiazarian, Pointwise shape adaptive DCT for high quality denoising and de blocking of grayscale and color images, IEEE Transaction on Image Processing 16(5)(2007).
- L . P . Yaroslavsky , Digital Signal Processing An Introduction , Springer ,Berlin, 1985.
- C.Tomasi,R.Manduchi, Bilateral filtering for gray and color images, in: Proceedings of the 1998 IEEE International Conference on Computer Vision, Bombay,India,1998,pp.839–846.
- D.Barash, A fundamental relationship between bilateral filtering, adaptive smoothing, and then on linear diffuse one equation, IEEE Transaction on Pattern Analysis and Machine Intelligence24(6)(2002)844–847.
- A.Buades,B.Coll,J.M.Morel,Areviewof image denoising algorithms, with a new one, Multiscale Modeling Simulation4(2)(2005)490–530.
- C.Kervrann,J.Boulanger, Optimal spatial adaptation for patch based image denoising, IEEE Transaction on Image Processing15(10)(2006) 2866–2878.
- K.Dabov,A.Foi,V.Katkovnik,K.Egiazarian , Image denoising by sparse3D transform-domain collaborative filtering, IEEE Transaction on Image Processing 16(8)(2007)2080–2095.
- M. Vetterli and C. Herley, \Wavelets and Filter Banks: Theory and Design," IEEE Transactions on Signal Processing, Vol. 40, 1992, pp. 2207-2232.
- W. Press et al., Numerical Recipes in Fortran, Cambridge University Press, New York, 1992, pp. 498-499,584-602.
Relevant Topics
- Advance Techniques in cancer treatments
- Advanced Techniques in Rehabilitation
- Artificial Intelligence
- Blockchain Technology
- Diabetes care
- Digital Transformation
- Innovations & Tends in Pharma
- Innovations in Diagnosis & Treatment
- Innovations in Immunology
- Innovations in Neuroscience
- Innovations in ophthalmology
- Life Science and Brain research
- Machine Learning
- New inventions & Patents
- Quantum Computing
Recommended Journals
Article Tools
Article Usage
- Total views: 15635
- [From(publication date):
May-2012 - Aug 29, 2025] - Breakdown by view type
- HTML page views : 10901
- PDF downloads : 4734