Improved Detection of ECG Features Using Wavelet for Emergency Medical Application

Department of Electronics and Telecommunication Engineering, Daffodil International University

^*Corresponding Author:

A.K.M Fazlul Haque
Department of Electronics and Telecommunication Engineering
Daffodil International University
E-mail: akmfhaque@daffodilvarsity.edu.bd

Visit for more related articles at International Journal of Advance Innovations, Thoughts & Ideas

Abstract

 Heart is one of the vital organs of human being. Cardiac activities of heart are also significant and very well known of medical sector. ECG (Electrocardiogram) contains very important clinical information about the cardiac activities of heart. The features of ECG signal may be extracted using FFT (Fast Fourier Transform) and Wavelet, especially for emergency medical situation. But it is difficult to extract the changes of small variation of ECG signal with time-varying morphological characteristics. So, it is needed to be extracted by signal processing method because there are not visible of graphical ECG signal. In this paper, an improved wavelet method has been proposed to extract the precise detection of small abnormalities of both simulated normal and noise corrupted ECG signal by writing MATLAB program. The proposed wavelet method found to be more summarized over conventional FFT and Wavelet in finding the small abnormalities of ECG signal.

Keywords

ECG, wavelet, FFT, Holter, cardiac, abnormality, feature extraction.

Introduction

ECG is an important diagnosis event for emergency cardiac patient. It is observed that patients’ do not get proper treatment due to the deficient of proper cardiac detection. In time domain morphological characteristic of quasi-stationary ECG signals contain very small abnormalities that would hamper the patient’s health. The signal frequencies are distributed (1) low frequency - P and T waves, (2) mid to high frequency-QRS complex [1,2,3]. Sudden pain or other organs of the body may cause the creation of sinusoids that may hamper the normal ECG pattern which is may be resulted small abnormalities. Generally it is not easy to detect these abnormalities in vision. In this regard, it is needed to extract some special features of ECG that may take an important role to find out the changes. A Holter monitor is an ECG recording done over a period of 24 or more hours. An automatic algorithm and software is needed to analyze this huge amount of 24 hours Holter ECG signals. Fourier transform is very well known technique which transforms time domain signal to frequency domain to get the frequency coefficients. But these coefficients do not carry time information. Short time Fourier transforms called windowing may be used to overcome this problem which has both time and frequency information. But the problem is the size of the window which is limited to all over the frequency. So, still there is a significant chance of ignoring a large amount of coefficient. The statistical properties of ECG wave are generally changed over time tending to be quasi-stationary. Recently wavelets have been used in a large number of biomedical applications. The wavelet packet method is a generalization of wavelet decomposition that offers a rich range of possibilities for signal analysis. Wavelet contains both time and scaled version. In order to extract the small changing coefficients which may understandable for paramedics, wavelet has found to be more précised. The multi-resolution framework makes wavelets into a very powerful compression [4] and filter tool [5], and the time and frequency localization of wavelets makes it into a powerful tool for feature extraction [6]. There are some works on precise detection of ECG using FFT and wavelet [7-17]. Karel et al. proposed the performance criteria to measure the quality of a wavelet, based on the principle of maximization of variance [8]. Mahmoodabadi et al. developed and evaluated an electrocardiogram (ECG) feature extraction system based on the multiresolution wavelet transform [9]. David et al. presented a method to reduce the baseline wandering of an electrocardiogram signal [10]. Shantha et al. discussed the design of good wavelet for cardiac signal from the perspective of orthogonal filter banks [12]. Nikolaev and Gotchev proposed a two-stage algorithm for electrocardiographic signal denoising with Wiener filtering in the translation-invariant wavelet domain [13]. Most of the works focused on the large size abnormalities with respect to extreme noisy channel using conventional FFT and wavelet method. Most of the clinically useful information in the ECG is found in the intervals and amplitudes defined by its features (characteristic wave peaks, frequency components, and time duration). In this paper, FFT and wavelet methods are developed for the extraction of small variations of the ECG signal. The proposed Wavelet method of signal processing is found to be superior to the conventional FFT and wavelet method in finding the small abnormalities in ECG signals.

Backgrounds

ECG signals both standard and noise corrupted have been generated using Matlab. These signals are analyzed by the wavelet method (Matlab wavelet Tool). Continuous wavelet transform (CWT) is defined as the sum over all time of the signal multiplied by scaled, shifted versions of the wavelet function ψ.

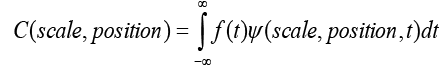
The results of the CWT are many wavelet coefficients C, which are a function of scale and position. Multiplying each coefficient by the appropriately scaled and shifted wavelet yields the constituent wavelets of the original signal.

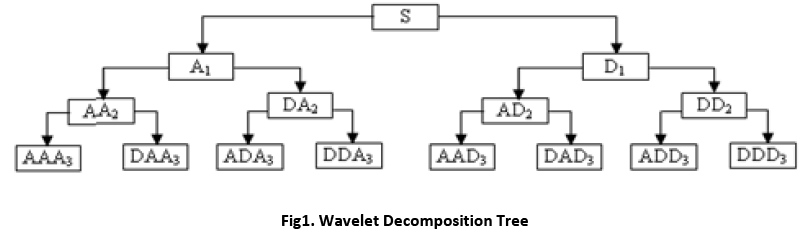
For many signals, the low-frequency content is the most important part. It is what gives the signal its identity. The high-frequency content, on the other hand, imparts flavor or nuance. To gain a better appreciation of this process, it is performed a one-stage discrete wavelet transform of a signal. The decomposition process can be iterated, with successive approximations being decomposed in turn, so that one signal is broken down into many lower resolution components. This is called the wavelet decomposition tree.

The wavelet packet method is a generalization of wavelet decomposition that offers a richer range of possibilities for signal analysis. In wavelet analysis, a signal is split into an approximation and a detail. The approximation is then itself split into a second-level approximation and detail, and the process is repeated. The Wavelet packet decomposition tree has been shown in Figure 1.

Figure 1: Wavelet Decomposition Tree.

Results and Discussions

The simulated normal ECG signals as well as the simulated noise corrupted signal have been implemented using FFT and wavelet for proper feature extraction. Sudden pain or other organs of the body may cause the creation of sinusoids that may hamper the normal ECG pattern which is may be resulted small abnormalities with very low frequency with approximately 0.5/1 Hz of the cardiac activities of heart. The algorithm has been given of the program with different parameters in below. The following algorithm has been used to evaluate the simulations output which are given step by step.

Algorithm:

Begin

//initialization

//parameters setting for ideal ECG signal

Set amplitude of ECG signal (a) = [3.5];

Set length of ECG signal (L) = [2700];

Set filter for smoothed ECG signal (y1) = [Savitzky-Golay FIR filter];

Set value of noise (n) = [1:30000];

Set value of time (t) = [0.00025:0.00025:7.5];

// parameters setting for power spectral density for Ideal ECG signal

Set fft point (fp) = [512];

Set frequency = [1000*(0:256)/512];

// parameters for noise adding in ECG signal

Set noise amplitude (na) = [0.1]

// parameters for noise corrupted ECG signal

Set filter type= [FIR1];

Set FIR1 order (or) = [31];

Set FIR1 normalized cutoff frequency (ct) = [.5];

// parameters for power spectral density for noisy signal

Set continuous wavelet transform scales (sc) = [1:64];

Set continuous wavelet wname (wn) = [sym4];

Set continuous wavelet coloration (col) = [abslvl];

//processing

Generating random value (del) = [round (L*rand (1))];

Discrete Fourier transform of ideal ECG signal (D) = [fft (d, fp)];

Complex Conjugate of D1=conj (D);

FIR filter design (nfilt) = [fir1 (or, ct)];

noise=[na*sin (pi*t)];

FIR filter with noise = [filter (nfilt, 1, noise)];

//output

Ideal ECG signal (signal) =y1 (n+del);

Magnitude of power spectral density for Ideal ECG signal = [D.* D1 / fp];

Noise=na*sin (pi*t);

Noise corrupted ECG signal (d) =signal+fnoise;

Coefficient1= cwt (signal, sc,'wn','col',[100 400]);

Coefficient2= cwt (d, sc,'wn','col',[100 400]);

End

Some important steps of the proposed algorithm have been described in below.

Step 1: Generation of standard ECG pattern having amplitude of 3.5mV and pulse repetition rate of 75 per minute.

Step 2: Generation of a noisy signal having frequency of 0.5/1 and amplitude of 0.1 mV which is 2.85 percent of the normal ECG signal.

Step 3: Generate the response of the normal and noise corrupted ECG signal using FFT method.

Step 4: Generate the response of the signal using wavelet method.

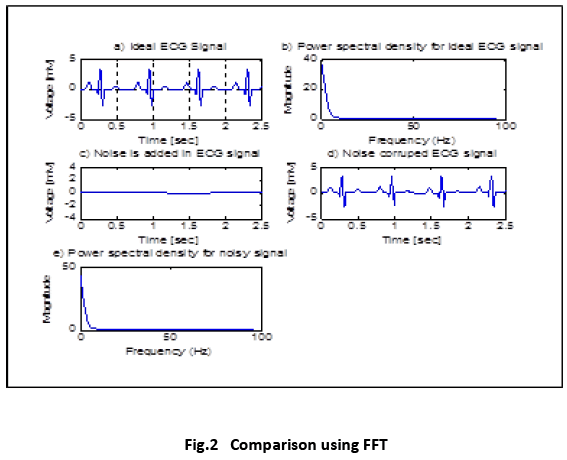
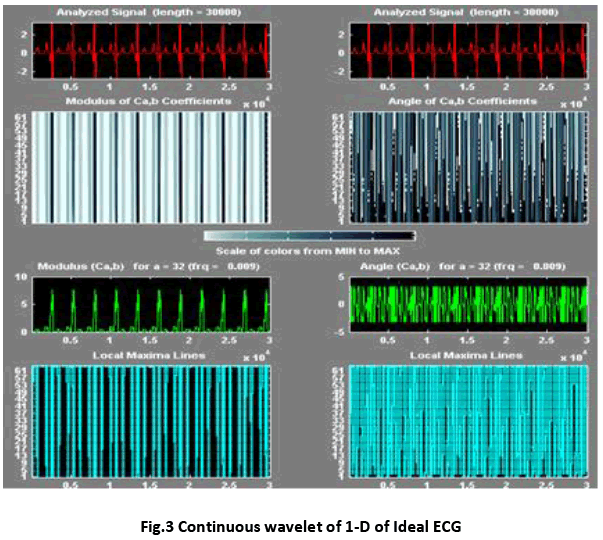
The FFT comparison of normal and small noise corrupted signal are simulated which is shown in Fig.2 and it cannot be identified the abnormalities using conventional FFT method. These dissimilarities are needed to record long time for proper diagnosis. Fig.3 shows the wavelet output of normal ECG signal and noise corrupted ECG signal. In Fig.3, the dissimilarities are identified by the statistical parameters of wavelet.

Figure 2: Comparison using FFT.

Figure 3: Continuous wavelet of 1-D of Ideal ECG.

Fig.1 shows the result of normal ECG and small noise corrupted signal which are simulated using FFT algorithm but have not found any significant changes. So it is obvious that the Fourier method, especially for this purpose does not convey an important issue to the paramedics to get a decision.

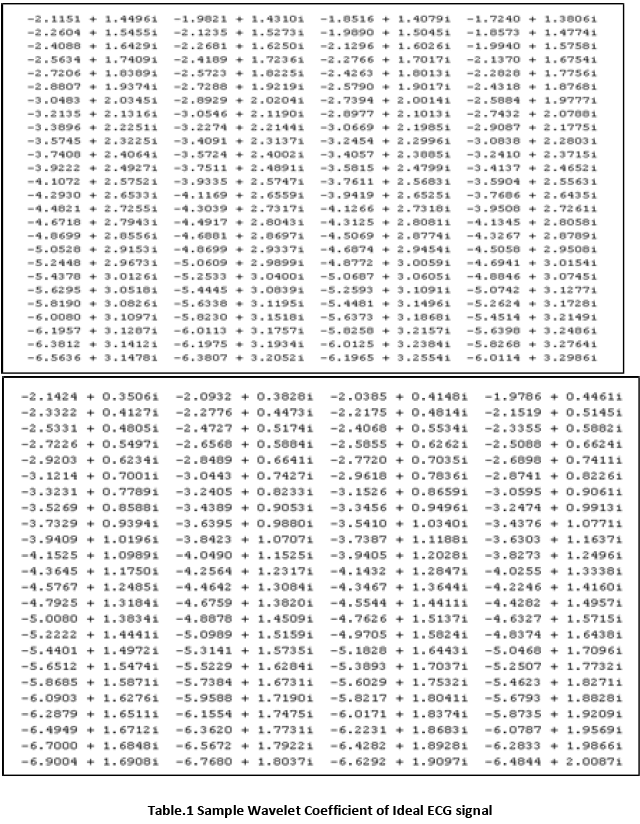
On the other hand, if wavelet is considered to demonstrate the same challenges, significant changing features are extracted from where paramedics get some particular decisions to diagnosis the proper treatment. Table 1 and 2 show the wavelet coefficients which are taken by the generation of program and show the differences between normal and noise corrupted ECG signal

Table 1: Sample Wavelet Coefficient of Ideal ECG signal.

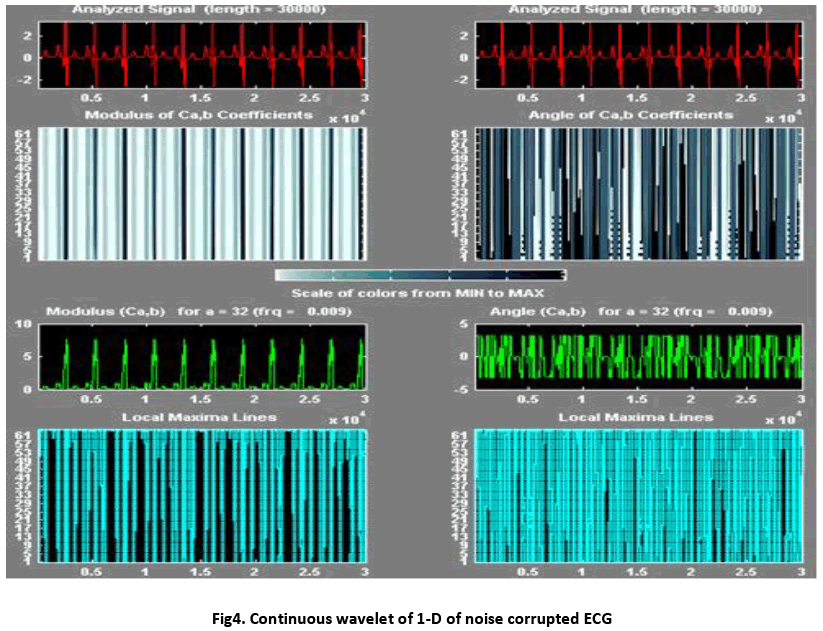
Fig.3 shows the presentation of wavelet coefficients which are extracted by the generation of program. There are some special parameters such as models, Angle, maxima and minima lines. The length of the parameters contains the feature of the coefficients.

Fig.4 shows the graphical representation of small noise corrupted ECG signal and which is also generated by the program. There are also same parameters as like as before and these parameters are compared with normal ECG graphical representation (fig.3). It is seen that the amplitude level of the angel, maxima, and minima of noise corrupted signal has been changed significantly compared to the normal ECG signal (fig.3).

Figure 4: Continuous wavelet of 1-D of noise corrupted ECG.

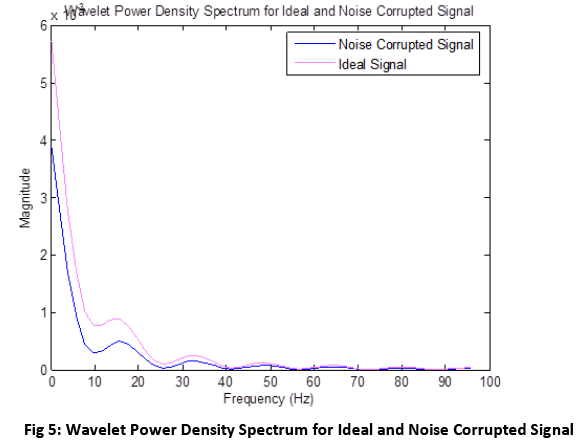
The power spectral density is also considered to find out the changes of the abnormalities. The power spectral density of both cases is also shown in fig.5. And the frequency versus magnitude level for ideal and noise corrupted ECG signal shows the dissimilarities clearly. The different values of data and graphical comparison prove obviously that wavelet has improved the feature extraction technique in finding the small abnormalities of ECG signal.

Figure 5: Wavelet Power Density Spectrum for Ideal and Noise Corrupted Signal.

Finally, it is notified that conventional FFT does not perform significantly to extract the information of small abnormalities of the ECG signal whereas the proposed wavelet method performs better in finding the small abnormalities of ECG signal than the other existing technique.

Conclusions

From the above discussion, it is observed that ECG signal may contain a small discontinuity due to the presence of sudden disordered of human being that is caused harmful to the cardiac function. To detect the precise feature of that signal, some offline simulated original signal and noise corrupted signal are generated, evaluated and tested using conventional FFT algorithm and proposed wavelet method. The above evidences based on FFT, wavelet, and power spectral density of both analysis say that the ECG feature extraction using proposed wavelet method behaves significant than other conventional system to find out the proper detection of small abnormalities of the ECG signal.

References

1. A.K. M. Fazlul Haque, Md. Hanif Ali, M. Adnan Kiber and Md. Tanvir Hasan, DETECTION OF SMALL VARIATIONS OF ECG FEATURES USING WAVELET. VOL. 4, NO. 6, AUGUST 2009’ ISSN 1819-6608, ARPN Journal of Engineering and Applied Sciences.
2. Thakor N.V, Webster, J.G. and Tompkins W.J. 1984. Estimation of QRS complex power spectra for design of QRS filter, IEEE Trans. Biomed. Eng. 31: 702-706.
3. Gramatikov B. 1993. Digital filters for the detection of late potentials, Med. Biol. Eng. Comp. 31: 416-420.
4. Gramatikov B. and Thakor, N. 1993. Wavelet analysis of coronary artery occlusion related changes in ECG. In: Proc. 15th Ann. Int. Conf. IEEE Eng. Med. Biol. Soc. Dan Diego. p. 731.
5. Ivo Provazn´ık and Jiˇr´ı Kozumpl´ık. 1997. Wavelet transform in electrocardiography data compression. International Journal of Medical Informatics. 45(1-2):111-128, June.
6. M.P. Wachowiak, G.S. Rash, P.M. Quesada, and A.H. Desoky. 2000. Waveletbased noise removal for biomechanical signals: a comparative study. IEEE Trans. Biomed. Eng. 47(3):360-368, March.
7. Cuiwei Li, Chongxun Zheng, and Changfeng Tai. 1995. Detection of ECG characteristic points using wavelet transforms. IEEE Trans. Biomed. Eng. 42(1): 21-28, January.
8. Karel J.M.H., Peeters R.L.M., Westra R.L., Moermans K.M.S., Haddad S.A.P. and Serdijn W.A. 2005. Optimal discrete wavelet design for cardiac signal processing, Proceedings of the IEEE, Engineering in Medicine and Biology 27th Annual Conference.
9. Mahamoodabadi S.Z., Ahmedian A., Abolhasani M.D. 2005. ECG feature extraction using daubechies wavelet, Proceedings of the fifth IASTED International Conference VISUALIZATION, IMAGING and IMAGE PROCESSING, September 7-9, Benidorm, Spain.
10. David Cuesta-Frau, Daniel Novak, Vladimir Eck, Juan C. Pérez-Cortés. 2002. Electrocardiogram Baseline Removal Using Wavelet Approximations, Computer-Based Medical Systems, (CBMS 2002), Proceedings of the 15th IEEE Symposium.
11. Gilbert Strang, Truong Nguyen. 1997. Wavelets and Filter Banks, Wellesley-Cambridge Press.
12. Soman K.P., Ramachandran K.I. 2004. Insight into wavelets from theory to practice. Prentice-Hall of India.
13. R. Shantha Selva Kumari, S. Bharathi, V. Sadasivam. 2007. Design of Optimal Discrete Wavelet for ECG Signal using orthogonal filter bank, International Conference on Computational Intelligence and Multimedia Applications, IEEE.
14. Nikolaev, Z. Nikolov, A. Gotchev, K. Egiazarian. 2000. Wavelet Domain Wiener Filtering For Ecg Denoising Using Improved Signal Estimate, IEEE.
15. Oktem R., Yaroslavsky L., Egiazarian K. 1998. Signal and Image De-noising in Transform Domain and Wavelet Shrinkage: A Comparative Study. Proceedings of EUSIPCO-98. pp. 2269-2272, Island of Rhodes, Greece. Sept.
16. Ghael S., Sayeed A., and Baraniuk R. 1997. Improved Wavelet Denoising via Empirical Wiener Filtering. Proceedings of SPIE. 3169: 289-299, San Diego. July.
17. Nikolaev N and Gotchev A. 1998. Denoising of ECG Signals using Wavelet Shrinkage with Time-Frequency Dependent Threshold. Proceedings of EUSIPCO-98, pp.2449-2452, Island of Rhodes, Greece. September.