Research Article Open Access
Kinetics of Biosorption of Three Heavy Metals by Five Free Microorganisms
| Nwidi IC* and Agunwamba JC | |
| Department of Civil Engineering, University of Nigeria, Nsukka Enugu State, Nigeria | |
| *Corresponding Author : | Nwidi IC Department of Civil Engineering University of Nigeria Nsukka Enugu State, Nigeria Tel: +2348032656399 E-mail: chineke_nwidi@yahoo.com |
| Received: February 25, 2016; Accepted: March 01, 2016; Published: March 05, 2016 | |
| Citation: Nwidi IC, Agunwamba JC (2016) Kinetics of Biosorption of Three Heavy Metals by Five Free Microorganisms. J Bioremed Biodeg 7:339. doi: 10.4172/2155-6199.1000339 | |
| Copyright: © 2016 Nwidi IC, et al. This is an open-a ccess article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. | |
Visit for more related articles at Journal of Bioremediation & Biodegradation
Abstract
In this paper, kinetics of biosorption of three heavy metals by five microorganisms was studied. The three heavy metals are zinc copper and manganese while the microorganisms are Bacillus circulans, Pseudomonas aeruginosa, Staphylococcus xylosus, Streptomyces rimosus and Saccharomyces cerevisiae. The investigation was carried out using non-vibrational flow-batch process. Two models were proposed to fairly accommodate all the mechanisms of biosorption at longer contact time. Also, the equation of a completely mixed flow was used to study the biosorption rate constant of the microorganisms within the detention time of 25 minutes inside the treatment units. Part of the data obtained from the laboratory was used for the calibration of the models while some parts were used for the verification. The verification was assessed using linear regression coefficient of correlation and average relative error. During the verification, the values of linear regression coefficients for the two models are 0.9978 and 0.9992 while average relative errors are 0.8768% and 4.4126% respectively. When compared with pseudo first and second order models, the values of coefficient of correlation obtained are 0.9965 and 0.9451 with corresponding average relative errors of 36.74% and 28.53% respectively. The values of biosorption rate constants for the microorganisms obtained from completely mixed equation are higher than those of concentration based models showing that the rate of biosorption is higher within the inception than towards equilibrium.
| Keywords |
| Biosorption; Kinetics; Contact time; Heavy metal; Biosorbent |
| Introduction |
| Some of human activities mainly in the industries such as electroplating, metallurgical, mining, painting and so on lead to release of heavy metals into the surrounding. Heavy metals are toxic pollutants. This means that heavy metal solution is a worldwide environmental problem [1-4]. Biosorption is a physiochemical process that occurs naturally in certain biomass which allows it to passively concentrate and bind contaminants onto its cellular structure [5]. The biological materials that have been investigated for heavy metal uptake include fungi [6], bacteria [7], yeast [8], micro-algae [9] and macroalgae [10]. Many of these materials are available in large quantities either as industrial waste by-products or from the natural sources. Biosorption has now evolved into a commercial process. Once the metal ion has diffused to the cell surface, it will bind to sites on the cell surface, which exhibits some chemical affinity for the metal. This step contains a number of passive accumulation processes and may include adsorption, ion exchange, coordination, complexation, chelating and microprecipitation [11]. The major advantages of biosorption over conventional treatment methods include: low cost, high efficiency, non-addition of nutrient requirements, minimization of chemical and or biological sludge, regeneration of biosorbent; and possibility of metal recovery [12]. Thus, kinetics studies give detailed information on adsorbate uptake rates and on rate-controlling steps such as external mass transfer, intraparticle mass transfer, and biosorptive reaction(s) [13]. Biosorption of metals is based on ion exchange mechanisms accompanied by release of light metals such as calcium, magnesium, potassium and sodium [14]. Due to the complexity of the biosorption mechanism, however, in theory, the order of a biosorption process must be determined by the general rate law equation, rather than pseudoorder kinetic equations [15,16]. This forms the basis of this research to obtain model(s) that could possible cover all the mechanisms of biosorption as contact time goes beyond 30 minutes using nonvibrational flow-batch reactors.Some of human activities mainly in the industries such as electroplating, metallurgical, mining, painting and so on lead to release of heavy metals into the surrounding. Heavy metals are toxic pollutants. This means that heavy metal solution is a worldwide environmental problem [1-4]. Biosorption is a physiochemical process that occurs naturally in certain biomass which allows it to passively concentrate and bind contaminants onto its cellular structure [5]. The biological materials that have been investigated for heavy metal uptake include fungi [6], bacteria [7], yeast [8], micro-algae [9] and macroalgae [10]. Many of these materials are available in large quantities either as industrial waste by-products or from the natural sources. Biosorption has now evolved into a commercial process. Once the metal ion has diffused to the cell surface, it will bind to sites on the cell surface, which exhibits some chemical affinity for the metal. This step contains a number of passive accumulation processes and may include adsorption, ion exchange, coordination, complexation, chelating and microprecipitation [11]. The major advantages of biosorption over conventional treatment methods include: low cost, high efficiency, non-addition of nutrient requirements, minimization of chemical and or biological sludge, regeneration of biosorbent; and possibility of metal recovery [12]. Thus, kinetics studies give detailed information on adsorbate uptake rates and on rate-controlling steps such as external mass transfer, intraparticle mass transfer, and biosorptive reaction(s) [13]. Biosorption of metals is based on ion exchange mechanisms accompanied by release of light metals such as calcium, magnesium, potassium and sodium [14]. Due to the complexity of the biosorption mechanism, however, in theory, the order of a biosorption process must be determined by the general rate law equation, rather than pseudoorder kinetic equations [15,16]. This forms the basis of this research to obtain model(s) that could possible cover all the mechanisms of biosorption as contact time goes beyond 30 minutes using nonvibrational flow-batch reactors. |
| Materials |
| In this study, the materials used are microorganisms comprising of gram positive, gram negative bacteria and algae which were supplied by Department of Microbiology, University of Nigeria Nsukka, while heavy metal solutions were prepared by dissolving metal copper nitrate, manganese sulphate and zinc chloride respectively (Cu(NO3)2·3H2O, MnSO4.4H2O and ZnCl2) in water to the required concentrations. These compounds were supplied by Nexill World Scientific Company located at E/1st Line Head Market, Onitsha, Anambra State, Nigeria. The biosorbents used are Staphylococcus xylosus, Bacillus circulans. Pseudomonas aeruginosa, Streptomyces rimosus and Saccharomyces cerevisiae. These microbes were grown and maintained on a mixture of nutrient broth and agar. The medium contains: soluble starch; beef extract; yeast extract; peptones; and NaCl (pH adjusted to 7.2). After a week of incubation at 33 ± 1°C, biomasses were harvested by means of centrifugation at 10,000 rpm for 10 minutes, washed twice with distilled water and then sun/airdried for 6 hours. At this point the microbes were ready for use in the biosorption experiments. |
| Biosorption experiments |
| Wastewater reservoir was filled with a mixture of water obtained from University of Nigeria, Nsukka Civil Engineering Laboratory and heavy metal. The mixture was diluted further until 50 mg/l of heavy metal in the solution was obtained, read with the aid of spectrophotometer. 2.5 g of biosorbent were introduced inside the treatment units respectively. The treatments plant comprises of a wastewater reservoir, five treatment units and five batch reactors connected by flow hoses. The treatment units have baffle to enhance mixing of the wastewater with the biosorbent. The flow is from wastewater reservoir to treatment units and finally into the batch reactors. During the 3 day period of operation, the units were monitored for 25 minutes while the reactors were monitored for 30 minutes, 2 hours, 24 hours, 48 hours and 72 hours respectively for metal ion concentration of the effluent solution and biosorption capacity (qt). |
| The pH of the treatment units and reactors was kept constant with the aid of 0.1m HCl and 0.1m NaOH buffer. Room temperature was also maintained throughout the experiment. |
| The metal concentrations of both the influents and effluents were obtained using a HI83200 Multiparameter spectrophotometer. The amount of metal adsorbed by biosorbent was calculated using the following balance equation: |
| Where qt is the metal uptake (mg/g); Co and Ct are the initial and timely metal concentrations in the solution (mg/l), respectively; V is the solution volume (ml) & M (g) is the mass of biosorbent. |
| Model formulation |
| Proposed kinetics of biosorption: The kinetics of biosorption were derived from general kinetic law and categorized in two ways namely: |
| I. A mass balance equation which assumes that the rate of change of ion concentration of heavy metal with time is proportional to change in concentration of the heavy such that, |
| K is adsorption constant, m is a decimal presumed to be less than 1 |
| Let |
| This implies that dU = dCt |
| where C1 is the constant of integration |
| Conditions, at t=0, Ct = C0 |
| Therefore, |
| Equation 17 can be rearranged to |
| This can be reduced to |
| And; |
| II. A mass balance equation which assumes that the rate of change of metal uptake of heavy metal with time is dependent on the metal uptake of that heavy metal such that, |
| K is adsorption constant, m is a decimal but must not be = 1 |
| Assumption: |
| Similarly, C1 (1− m) is a constant of integration to be represented by C2 |
| Therefore, |
| To obtain the value of m, equation 13 becomes |
| let |
| By applying binomial theorem |
| For equation 16 to converge, |
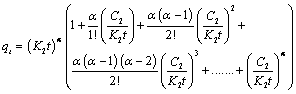 (17) (17) |
| Outside the first multiple, (K2t)α, the addition of other multiples will be taken as constant C. |
| This means that: |
| The final modified Adsorption constant K = K2α |
| From the slope of a graph of ln qt against ln t, the value of α was obtained |
| Description of bisorption using completely-mixed flow equation |
| At the treatment unit, completely-mixed flow was assumed and hence, using a mass-balance equation, the biosorption constants for the biosorbents were obtained [17]. |
| Accumulation=inflow-outflow+decay (Adsorbed heavy metal) |
| Mathematically, |
| Where; V denotes the volume of the reactor; C0 and C are the influent and effluent waste concentrations respectively, K is assumed to be the adsorption coefficient of a particular biosorbent and Q represents the flow rate. By dividing through by V in equation 22, |
| Let |
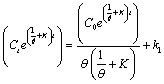 (28) (28) |
| Condition: at t=0, Ct = C0 |
| Assuming steady state |
| Equation 31 can be written as: |
| Where Ө = detention time, the number of minutes the wastewater spend in the treatment unit before finally moving into the batch reactor/reservoir. |
| Calibration and verification of proposed equations |
| The models were formulated using multiple regression equations based on measured data. It was later verified with independent set of data to know how the models would behave outside the data which they was formulated. The two models are: |
| The two most popular kinetic models pseudo first and second order models were used to compare with the performance of the two proposed models. The pseudo models are represented by equations 20, 21 below. |
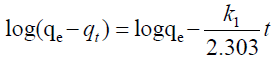 |
| Where; |
| qe (mg/g) and qt (mg/g) are the sorption capacities at equilibrium and at time t (min), respectively and k1 (1/min) and k2 (1/min) are the rate constants of pseudo first and second order kinetic models. |
| The linear regression coefficient of correlations were calculated using the following representative of x and y. (x represent time abscissa, y represent ordinate) |
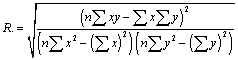 (35) (35) |
| Similarly, average relative errors were calculated from the following equation. |
| Where Xe,meas. is the measured variable, Xe,calc. is the calculated variable and N is the number data points [18]. |
| Results and Discussion |
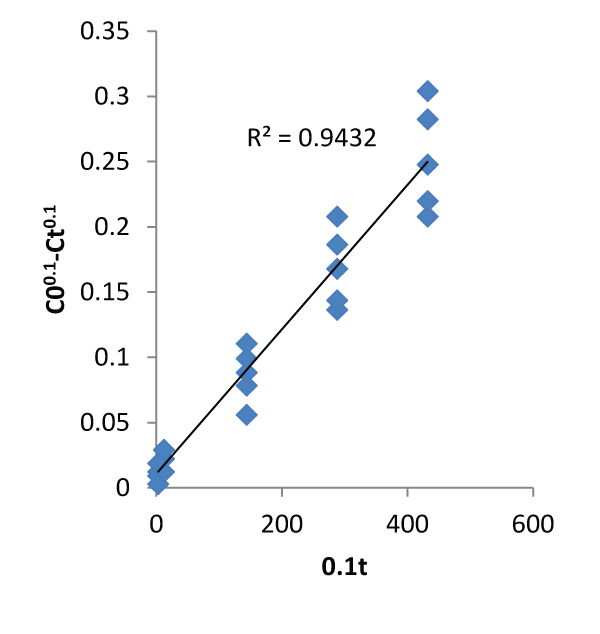
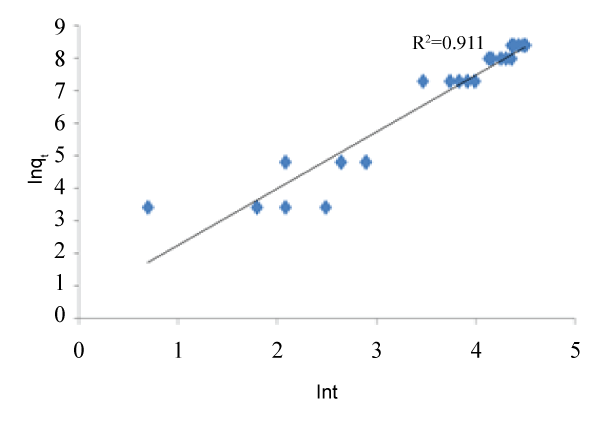
| The graphs of the concentration against time and natural logarithm of metal uptake capacity against time are shown below. In other words, Figures 1 and 2 below were used to calibrate the two proposed kinetic equations. While the former assumes kinetics in terms of Concentration, the latter assumes kinetics in terms of metal uptake capacity. The value of m was found to be 0.9 which when applied gives the first proposed kinetics model as: |
| Similarly, from the variation of ln qt against ln t, the slope gives the value for the power of t. the value was found to be 0.525 and therefore, the second kinetics model becomes: |
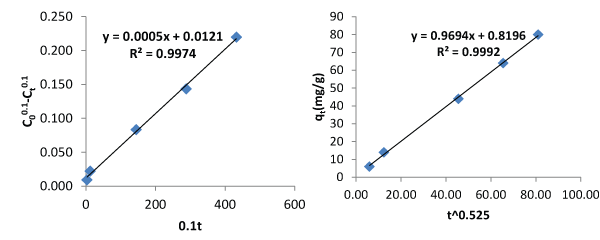
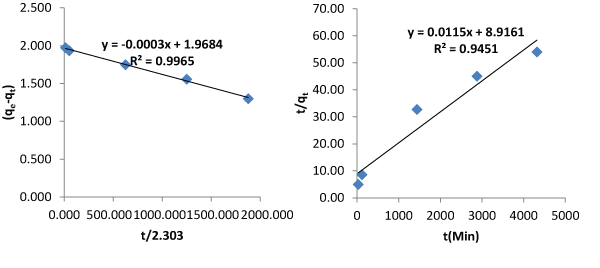
| Tables 1 and 2 are the verification of the two proposed models. Their average relative errors are 0.8768% and 4.4126% respectively. Tables 3 and 4 are description of the kinetics using Pseudo first and second order kinetic models using the same data. Pseudo first and second order models produced average relative errors of 36.7374% and 28.5263%. This has shown that the two proposed models can perform better than others at contact time beyond few hours. |
| Figures 3 and 4 describe the kinetics of biosorption of zinc by Saccharomyces cerevisiae using the two proposed kinetic models and pseudo first & second order kinetic models. From Figure 3, the slope of the plots represents the rate of reaction which implicitly is the kinetics of biosorption of zinc by Saccharomyces cerevisiae. The rate constants by first and second proposed models from the above relationships are 0.0005 per minute and 0.9694 per minute while those of Pseudo first and second models are -0.000348 per minute and 0.00015 per minute respectively. The choice of rate constant depends on the values of average relative error and linear regression coefficient of correlation. The kinetic model with highest value of linear regression coefficient of correlation and lowest value of average relative error should be chosen in preference to others. |
| The pH of the solution was maintained at 6 g, 2.5 g of biosorbents and 50 mg/l concentration of the heavy metals were used for optimum biosorption at room temperature, throughout the experiment. As expected, from Table 5, the biosorption rate constant for a completely mixed flow equation is higher than that of combined flow and batch process when compared to concentration based kinetic equations. The high values of K as shown on Table 1 above indicates that biosorption rate is higher during the starting than towards equilibrium. |
| Judging by the values of linear regression coefficient of correlation for a completely mixed-flow equation, it could be inferred that the biosorption rate is consistent within the first twenty five minutes of the detention time for all the five microorganisms. Also the high value of biosorption rate constant (K) for the biosorption of zinc by Staphylococcus xylosus explains why it reached equilibrium concentration within 24 hours. This means that Staphylococcus xylosus has greater values of biosorption coefficients for the biosorption of copper and manganese within the first 25 minutes. Staphylococcus xylosus should therefore be recommended when biosorption in a free flow reactor with a considerable detention time is to be constructed. |
| Conclusion |
| Most of the existing kinetic models limit the coverage of mechanisms of biosorption to one or two aspects. The mechanisms of biosorption are the rate controlling steps. This limitation of the existing models to one or two aspects accounted why they produce low values of linear regression coefficient of correlation as contact time goes beyond 30 minutes. In this work, the first and second proposed kinetic models were applied to an independent data and they produced average relative errors of 0.8768% and 4.4126 respectively. The performance of the two proposed kinetic models and pseudo first and second kinetic models on the independent data are as presented on Figures 3 and 4. The two proposed kinetic models produced relatively high values of coefficient of correlation of 0.9974 and 0.9992. In comparison, pseudo first and second order kinetic models produced the following values of linear coefficient of correlation, 0.9965 and 0.9451 with corresponding values of average relative errors of 36.7374% and 28.5263%. From the above results it is imperative to test the performance of kinetic models with other parameters like average relative error instead of only regression coefficient of correlation. The first and second proposed equations have high values of coefficient of correlation and low values of average relative error whereas the pseudo first and second order models have moderate values of coefficient of correlation but very high values of average relative error. The bases of selection should be based on high value of coefficient of correlation and low value of average relative error. From above, it is clear that when contact time goes beyond 30 minutes, the proposed models are preferable in describing the kinetics of biosorption of heavy metals using microorganisms at room temperature. |
| References |
References
|
Tables and Figures at a glance
| Table 1 | Table 2 | Table 3 | Table 4 | Table 5 |
Figures at a glance
 |
 |
 |
 |
| Figure 1 | Figure 2 | Figure 3 | Figure 4 |
Relevant Topics
- Anaerobic Biodegradation
- Biodegradable Balloons
- Biodegradable Confetti
- Biodegradable Diapers
- Biodegradable Plastics
- Biodegradable Sunscreen
- Biodegradation
- Bioremediation Bacteria
- Bioremediation Oil Spills
- Bioremediation Plants
- Bioremediation Products
- Ex Situ Bioremediation
- Heavy Metal Bioremediation
- In Situ Bioremediation
- Mycoremediation
- Non Biodegradable
- Phytoremediation
- Sewage Water Treatment
- Soil Bioremediation
- Types of Upwelling
- Waste Degredation
- Xenobiotics
Recommended Journals
Article Tools
Article Usage
- Total views: 12340
- [From(publication date):
March-2016 - Aug 24, 2025] - Breakdown by view type
- HTML page views : 11197
- PDF downloads : 1143
