Review Article Open Access
Mathematical Modeling in Anaerobic Digestion (AD)
| Liang Yu, Pierre Christian Wensel, Jingwei Ma and Shulin Chen* | |
| Department of Biological Systems Engineering, Washington State University, Pullman, WA 99164, USA | |
| Corresponding Author : | Shulin Chen Department of Biological Systems Engineering Washington State University, Pullman, WA 99164, USA Tel:509-335-3743 Fax: 509-335-2722 E-mail: chens@wsu.edu |
| Received June 09, 2013; Accepted July 31, 2013; Published August 02, 2013 | |
| Citation: Yu L, Wensel PC, Ma J, Chen S (2013) Mathematical Modeling in Anaerobic Digestion (AD). J Bioremed Biodeg S4: 003. doi:10.4172/2155-6199.S4-003 | |
| Copyright: © 2013 Yu L, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. | |
Related article at Pubmed Pubmed  Scholar Google Scholar Google |
|
Visit for more related articles at Journal of Bioremediation & Biodegradation
Abstract
Anaerobic digestion (AD) of biowastes is the most conventional way to produce methane-rich biogas, which has great potential to replace the fossil fuel used in multiple applications, like vehicular transportation. Many countries and companies are involved in the design and construction of AD systems. Both efficient and economical AD performances are extremely important to promote worldwide adoption of this technology. Empirical methods have been traditionally used to scale up AD facilities, but these have required construction of expensive prototype systems and time-consuming studies. Alternatively, design and optimization of AD processes for biogas production can be enhanced via validated mathematical models developed from mechanistic studies that lead to a more indepth understanding of the very complex transport phenomena, microbial biochemical kinetics, and stochiometric relationships associated with AD. This paper provides a comprehensive literature review on the models available for AD processes.
| Keywords |
| Anaerobic digestion (AD); Mathematical model; Kinetics; ADM1; Computational Fluid Dynamics (CFD) |
| Introduction |
| Anaerobic digestion (AD) has become an increasingly important industrial process. AD is a green technology involving the generation of methane-rich biogas via the biological degradation of regionallyavailable biomass like agricultural and municipal solid wastes and wastewaters. AD processes have for many years been used to treat and sanitize sewage sludge waste from aerobic wastewater and animal manure, reduce its odor and volume, and produce useful biogas. Biogas in turn is a first generation, renewable biofuel that offers the prospect of replacing fossil fuels in the transportation sector and limiting the net greenhouse gas emissions implicated in climate change [1]. |
| Between 1950-1980, high production-rate systems were developed and used to process effluents from agricultural and industrial sectors. Processing of effluents that contained toxic and recalcitrant compounds from the pulp/paper, petrochemical, and other chemical industries was later possible as both technology and knowledge pertaining to toxicity and biodegradability were enhanced [2]. AD technology has been widely adopted by Germany and Denmark, which have implemented rigorous waste disposal legislation. Since 2000, annual electricity generation from digester projects in the USA has increased almost 25- fold from 14 million kilowatt-hours (kWh) to an estimated 331 million kWh per year [3]. |
| The majority of current agricultural biogas facilities digest chicken, cow, and pig manure with co-substrates supplemented to increase the organic material content and gas yield [4]. Such co-substrates have routinely included harvest residues (e.g. Sugar beet leaves and tops), agricultural organic wastes (e.g. energy crops), and municipal food and waste bio-waste collected from restaurants and households [4-6]. The typical composition for common AD substrates is presented (Table 1). Substrate digestibility and biogas production are affected by substrate salinity, loading rate, mineral and volatile fatty acid composition, carbon-to-nitrogen ratio, and pH, as well as reactor temperature and Hydraulic Retention Time (HRT) [7-9]. Compared to AD systems in rural areas, those in urban settings require higher retention of biomass, smaller reactor volumes, shorter hydraulic retention times, and higher loading rates. |
| Understanding process mechanisms and kinetics is required for good reactor design where operating conditions, methane (CH4) production, system stability, and effluent quality can be predicted or specified. Various models have been constructed to provide greater indepth understanding of the mechanisms influencing the bio-chemical AD process. Since the initial dynamic mathematical digester models of the late 1960s [10,11], additional and more complex models have been developed to account for significant microbial interactions and inhibitions [12-14]. |
| Ideally, process models are supposed to describe the qualitative and quantitative aspects of microbial reactions, ranging from hydrodynamics and mass transfer to population dynamics in different reactor configurations under different environmental and operational conditions. However, the task of obtaining valid required kinetic constants is complicated by the fact that AD is itself a complicated multi-stage dynamic process that entails the concerted effort of several bacterial groups of bacteria. The composition of such groups varies in an unknown manner with changes in retention time, feedstock, temperature, reactor type, and other operating conditions. |
| The task is further complicated by the lack of a valid and reliable method for quantifying microbial cell biomass in digesters containing insoluble substrates. The predictive power of AD models is limited by the lack of knowledge regarding the specific bacteria involved and their metabolism and physiological limitations. Therefore, current efforts to develop a feasible AD model typically rely on assumptions that in turn lead to the convenient disregard of real-world phenomena and nonidealities. The objective here is to review the existing scientific literature as it pertains to development of models that involve, among other things, reactor kinetics and mixing, to enhance anaerobic digester design, optimization, scale-up, and operation. |
| Anaerobic Digestion Pathways and Reactions |
| Overall, the bio-chemical reactions occurring during AD can be classified as heterogeneous reactions (i.e. hydrolysis) and homogeneous reactions (i.e. acidogenesis, acetogenesis and methanogenesis). These very complex reactions transpire via a consortium of microorganisms which includes enzyme-secreting, fermentative, H2-consuming, H2- producing, acetogenic, CO2-reducing, and aceticlastic methanogenic bacteria [4,5]. |
| These AD reactions result in the formation of intermediates, release, their dissolution into the aqueous phase, and their metabolic conversion into products. Death and lysis of viable bacteria, such as anaerobic decomposition of viable, biological solids (e.g. waste activated sludge, algae), is first needed prior to the uptake of organic compounds. Organic compounds in the sludge (e.g. lipids, proteins, and carbohydrates) are then biologically decomposed by extra-cellular enzymes (e.g. lipase, protease, and cellulase) to small and soluble products that can then be transported across bacterial cell membranes and undergo various intra-cellular metabolic processes. There they are converted to intermediate compounds like fatty acids, amino acids, acetic acids, sugars, and H2, which are ultimately converted to biogas comprised primarily of methane (CH4) and carbon dioxide (CO2) [15]. |
| The three temperature regimes generally operated for anaerobic digesters are psychrophilic (10–25°C), and more frequently, mesophilic (25–45°C), and thermophilic (45–65°C). Constant temperature during AD must be maintained to avoid temperature fluctuations that adversely impact biogas production. Facilities running at thermophilic temperatures are usually lower in methanogenic diversity, more sensitive to temperature fluctuations, and need more time to adapt to a new temperature [16,17]. Mesophilic bacteria can withstand ± 3°C temperature fluctuations without greatly sacrificing CH4 production. The speed and efficiency of an AD process are enhanced by the higher methanogenic bacterial growth rate at thermophilic process temperatures. Compared to a digester operated at mesophilic temperatures, one at thermophilic temperatures can therefore be loaded to a higher extent or operated at a lower Hydraulic Retention Time (HRT). However, ammonia toxicity and the risk of wash-out of microbial populations increases with increasing temperature, potentially leading to greater imbalance and ammonia inhibition [18]. |
| The generation of CH4 (a.k.a. methanogenesis) occurs within a relatively narrow pH range of 6.5-8.5 and optimally between 7.0-8.0. This differs from the ideal pH range for hydrolysis (5.5–6.5) [19,20]. At pH<6 or pH>8.5, methanogenesis is significantly inhibited. The pH generally increases with increasing concentration of ammonia arising from protein decomposition, and decreases with increasing concentration of key process intermediates like Volatile Fatty Acids (VFA) [21]. However, substrate buffer capacity, such as that found in the surplus alkalinity of animal manure, will in many cases prevent a pH decrease from VFA accumulation. Acetic acid is normally the most concentrated of carboxylic acids but is less inhibitory to methanogens than propionic and butyric acids [22,23]. Acidogenic bacteria generate organic acids that decrease digester pH [24] and have higher growth and reproductive rates than methanogenic bacteria. A twostage or multi-stage digestion system reportedly maximizes control over digester bacterial communities. Hydrolysis, acetogenesis, and acidogenesis normally occur within the first stage. This reactor buffered the feedstock addition rate. Organic matter was then heated to the required operational temperature (either mesophilic or thermophilic) before it was pumped into a methanogenic reactor [25]. |
| Increasingly complex models for metabolic reactions have been developed with the recognition of various microbial groups and substrates in AD systems [12]. However, the difficulty in identifying the composition of complex, undefined substrates led to previous efforts to simulate co-digestion of various wastes that for simplicity were assumed to be defined by general compositions. For example, waterwaste was assumed to be composed of carbohydrates, proteins, lipids and others [26].The more advanced AD substrate pathways and stochiometry based on these assumptions [27] were presented in the following Angelidaki et al. [12] model and Anaerobic Digestion Model No.1 (ADM1) model [13]. |
| A comprehensive model of anaerobic bioconversion |
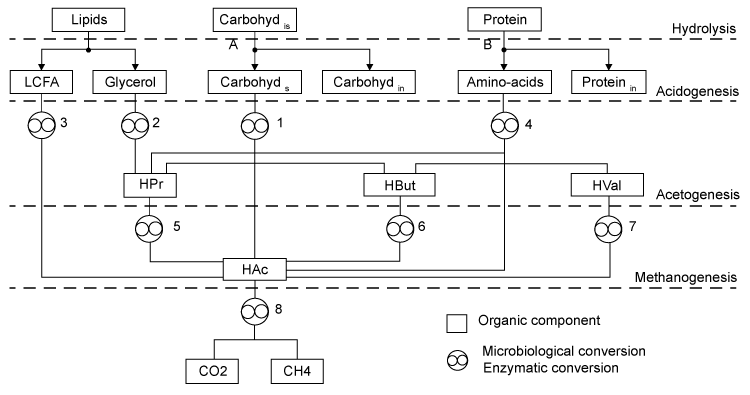
| A comprehensive model detailing the generation and degradation pathways of intermediates with associated interactions was previously developed by Angelidaki et al. [12]. This simulates co-digestion of complex wastes having different characteristics and compositions via the main pathways depicted (Figure 1). The model features the enzymatic hydrolysis of undissolved carbohydrates and undissolved proteins. It also involves eight types of bacteria. These include (1) glucose-fermenting acidogens, (2) lipolytic bacteria, (3) LCFAdegrading acetogens, (4) amino acid-degrading acidogens, (5) propionate, (6) butyrate, (7) valerate-degrading acetogens, and (8) aceticlastic methanogens. To achieve reasonable accuracy without actual physical experimentation, the model’s assumed waste composition is conveniently generalized and defined by the following compounds that are routinely measured: |
| Carbohydrates: The model classifies carbohydrates as soluble, insoluble, and inert. Insoluble carbohydrates (C6H10O5)is are hydrolyzed by enzymes to soluble (C6H10O5)s and inert carbohydrates (C6H10O5)in [12]. |
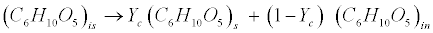 (R1) (R1) |
| where Yc represents the fraction of carbohydrates that are degradable. |
| Soluble carbohydrates are further degraded to acetate (C2H4O2), propionate (C3H6O2), butyrate (C4H8O2) in the following acidogenic step [18]: |
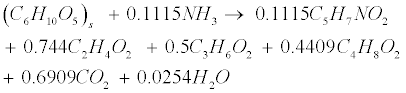 (R2) (R2) |
| Propionate (C3H6O2) and butyrate (C4H8O2) are degraded to acetate (C2H4O2) and hydrogen (H2) in the following acetogenic steps [29]: |
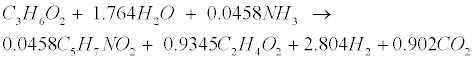 (R3) (R3) |
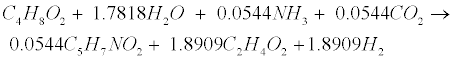 (R4) (R4) |
| An empirical formula C5H7NO2 is used to represent biomass. The two pathways to generate methane (CH4) in the methanogenic step involve (1) hydrogen-using methanogenesis including Equation (R3’) and Equation (R4’) which are derived from the propinic step [Equation (R3)] and the butyrate step [Equation (R4)], respectively, and (2) aceticlastic methanogenesis, a primary methanogenic step where acetate is broken down to evolve CH4 and CO2 as follows [28]: |
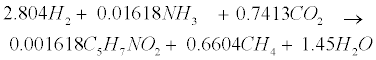 (R3’) (R3’) |
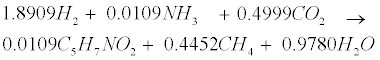 (R4’) (R4’) |
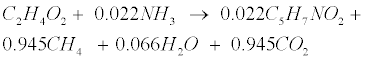 (R5) (R5) |
| Lipid: Since oleate in many vegetable oils is the most abundant type of long-chain fatty acids (LCFA, C18H34O2), the model assumes glycerol trioleate (GTO, C57H104O6) as standard lipid. Decomposition of GTO involves (1) lipolysis to oleate and glycerol (C3H8O3) and (2) glycerol degradation to biomass (C5H7NO2) and propionate (C3H6O2) as follows [12]: |
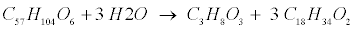 (R6) (R6) |
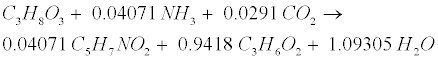 (R7) (R7) |
| Decomposition of the oleate produced by LCFA-degrading acetogens involves a combination of the LCFA (R8) and hydrogenusing (R9) steps [12]: |
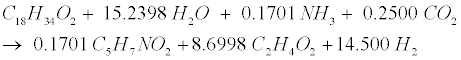 (R8) (R8) |
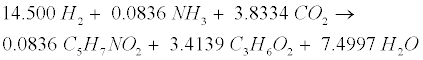 (R9) (R9) |
| After the LCFA (R8) and hydrogen-using (R9) steps, propionate (C3H6O2) is further degraded to acetate (C2H4O2), CO2 and H2 in the acetogenic (R3) step. Then the methanogenic (R3’), (R4’) and (R5) steps are carried out to generate CH4. |
| Protein: The model assumes gelatin (CH2.03O0.6N0.3 S0.001) as standard protein. Proteins are first hydrolyzed to amino acids as follows [12]: |
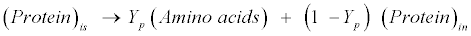 (R10) (R10) |
| where Yp represents the fraction of protein that is degradable. Acidogenic bacteria then additionally decompose amino acids (CH2.03O0.6N0.3S0.001) to volatile fatty acids (VFAs) as follows [12]: |
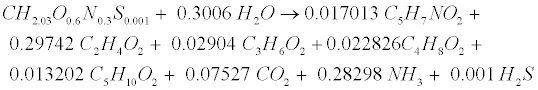 (R11) (R11) |
| Primary acids generated during gelatin decomposition include acetate (C2H4O2), propionate (C3H6O2), butyrate (C4H8O2), and valerate (C5H10O2). Valerate decomposition was experimentally determined as follows [12,18]: |
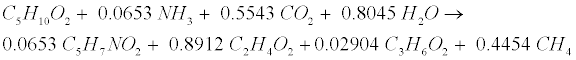 (R12) (R12) |
| Like Lipid, protein conversion to acetate involves sequential aceticlastic methanogenesis reactions described by Equation (R5) to split them to CH4 and CO2. Propionate (C3H6O2) and H2 go though the acetogenic (R3) step and hydrogen-using methanogenesis (R3’) and (R4’) steps to generate CH4. |
| As further described in upcoming section, hydrolytic steps here are assumed to follow 1st-order reaction rate laws with inhibition by total VFAs that include acetate, propionate, butyrate, and valerate. Acidogenic, acetogenic, and methanogic reactions are assumed to adhere to Monod growth kinetics with respect to their primary substrates. A growth rate-dependence on temperature, pH, and ammonia concentration is assumed for all bacteria reactions. |
| Anaerobic digestion model No.1 (ADM1) model |
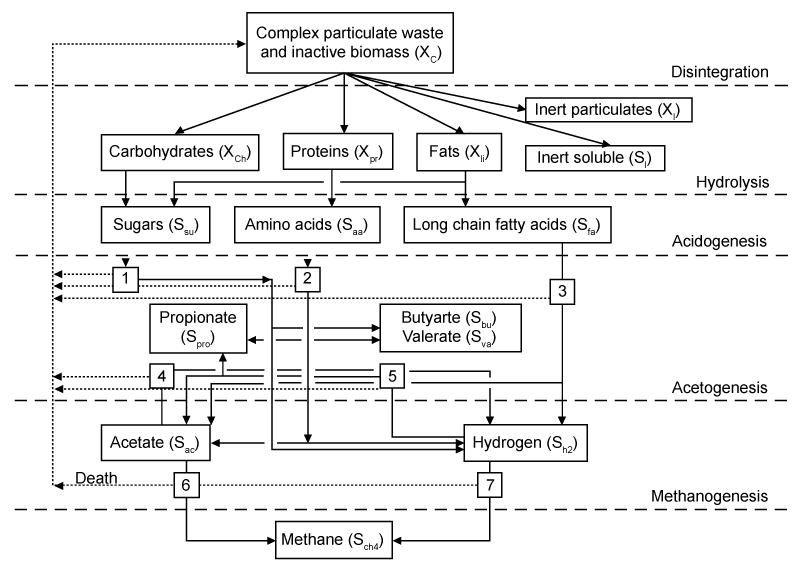
| The International Water Association (IWA) ADM1 model was developed as a result of international collaboration among experts from multiple anaerobic process technology disciplines [13,29]. The collaboration’s primary aim was to create 241 a tool to overcome the limitations of previously developed models. These were mainly attributed to their over-specificity and inability to be more widely applied. Conventional nomenclature, measurement units, and model structure in agreement with the pre-existing and popular activatedsludge and anaerobic digester models from literature [13] were implemented during ADM1 model development. Conventional process variables like discretized organic acids and ammonium concentrations, sludge pH, and gas flow rates were also used as model outputs. Specificities or peculiarities for certain processes were omitted from the model to make it more generic and usable. Therefore, the ADM1 model can be regarded as a widely-applicable, baseline, or uniform platform that further welcomes any necessary application-specific refinements or modifications of certain processes. |
| The structured ADM1 model simulates major processes associated with converting complex organic substrates into CH4, CO2, and inert by-products (Figure 2) [13,30]. Biochemical rate coefficients (vi,j) and kinetic rate equations (ρj) for soluble and particulate components (i=1-12; j=1-19), can be reffered to Batstone et al. [13]. The ADM1 model simulates degradation of complex solids into proteins, fats, carbohydrates, and inert compounds. These degradation products are then hydrolyzed to amino acids, long chain fatty acids (LCFA), and sugars, respectively. Volatile organic acids and H2 gas can then be generated via the acidogenic fermentation of proteins and carbohydrates. Fermentation of proteins and carbohydrates, acetate and H2 gas are also generated via anaerobic oxidation of LCFA or acetogenic conversion of propionate, butyrate, and valerate. CH4 is produced by both aceticlastic methanogenic cleavage of acetate and hydrogenotrophic methanogenic reduction of CO2 by H2. The specific chemical equations for these processes can be referred to the aforementioned R1–R12 [12,18,28]. |
| As further described in section 3, the ADM1 model involves complex reaction kinetics and a multitude of simultaneous and sequential reactions, primarily classified as either biochemical or physico-chemical. Extra-cellular enzymes are assumed to typically catalyze biochemical reactions involving biologically-available organic substrates. All extra-cellular ADM1 biochemical reactions are assumed to adhere to empirically-based 1st-order rate law kinetics, and all intra-cellular ADM1 biochemical reactions are assumed to adhere to Monod-type substrate uptake kinetics. Substrate uptake reaction rates are proportional to the biomass growth rate and biomass concentration [13]. |
| One of two empirical functions expresses pH inhibition for all bacterial groups. Non-competitive functions express H2 and free ammonia inhibition for acetogenic and aceticlastic methanogenic bacterial groups, respectively. Secondary Monod uptake kinetic equations are used to account for growth limitation when inorganic nitrogen in the form of either ammonia or ammonium becomes limited. Competitive uptake kinetic expressions account for consumption of butyrate and valerate by acetogenetic bacteria. Physico-chemical reactions are independent of microorganisms. These are instead assumed to be controlled by processes like those involving gas-liquid transfer and those involving ion association/dissociation (a.k.a. equilibrium), which are relatively faster than biochemical processes and can be expressed by algebraic, as opposed to differential, equations. Liquid-gas transfer processes are represented by the two-film theorybased dynamic gas transfer equations. |
| The ADM1 model has been widely applied and validated in simulating the anaerobic digestion of several organic wastes like industrial wastewaters [31], sludge from wastewater treatment plants [30,32], sewage sludge [33], black water from vacuum toilet [34], and olive mill solid wastes [35]. There are two types of ADM1 model applications: One involves applications of the standard model in a mixed tank as mandated by the ADM1 Scientific and Technical Report [13,36], frequently to monitor specific systems. The other involves application in theoretical analysis for new distributed parameters. |
| Complex models like ADM1 are well suited for process simulation. However, they are substantially limited when applied for process control and optimization [37]. The ADM1 model assumes to simulate a constant-volume, completely-mixed system [13]. However, at larger-scales, it is difficult to encounter ideal mixing in any digester, and the actual complex flow behavior likely would limit ADM1 model’s predictive accuracy. Furthermore, ADM1 model complexity leads to the need for many input parameters, ultimately resulting in a multitude of stoichiometric and kinetic equations. Parameter identification and manipulation of many equations can prove arduous. Depending on the substrate being digested, usually a small number of parameters significantly affect models’ outputs. Also, despite the adequate representation of relevant physical processes by ADM1 model assumptions, many reactions can occur rapidly and not affect the overall process dynamics. |
| Bio-chemical Kinetics |
| Overview |
| The theory of continuous cultivation of microorganisms has been previously used to mathematically represent biological treatment process kinetics [38,39]. Biological kinetics for many models are here based on the elementary microbial growth and substrate consumption rates which depend on a growth-limiting substrate concentration. Nurients are assumed to be substrates that are supplied in excess. The following equations are some common kinetic expressions describing anaerobic treatment processes: |
| First order kinetic model [40]: |
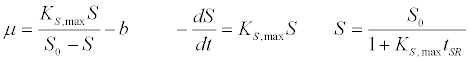 (1) (1) |
| Grau et al. [41] kinetic model: |
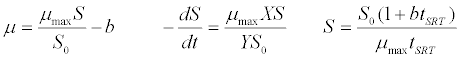 (2) (2) |
| Monod kinetic model [42]: |
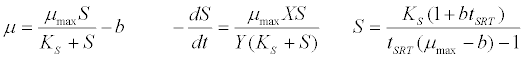 (3) (3) |
| Contois kinetic model [43]: |
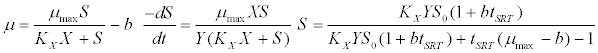 (4) (4) |
| Chen & Hashimoto kinetic model [44]: |
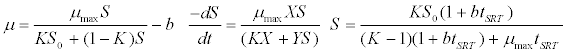 (5) (5) |
| Haldane kinetic model [45]: |
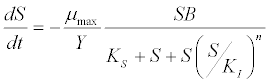 (6) (6) |
| where μ is the specific growth rate; μmax is the maximum specific growth rate; n is the Haldane index (n=1 or 2); S0 and S are the concentrations of the growth-limiting substrate in the influent and effluent for a continuous stirred tank reactor (CSTR) reactor at steady state, respectively; X is the microorganism concentration; KS,max is the maximum specific substrate use rate; b is thespecific microorganism decay rate; tSRT is the solid retention time (a.k.a mean cell residence time); Y is growth yield coefficient; μmax is the maximum specific growth rate; KX is Contois kinetic constant; K is the Chen and Hashimoto dimensionless kinetic constant; B is the concentration; KS is the half saturation coefficient; KI is the inhibition constant. |
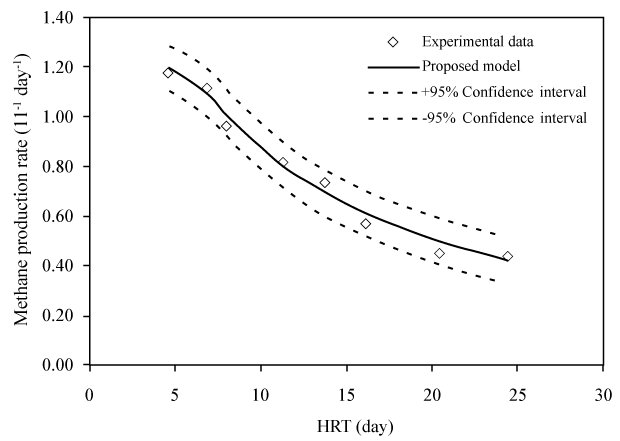
| These equations comprehensively represent the fundamental framework for AD process simulation [30]. Many kinetic models based on these equations, like ADM1 and Angelidaki et al. [12] model, were modified and applied to simulate different AD processes and predict their productivity [46-48]. For instance, the high level of agreement between such model prediction of CH4 production rate and experimental measurement data is revealed as a good curve fit with a confidence interval of 95% (Figure 3). Here the CH4 production rate (G) is estimated as [46]: |
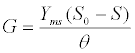 (7) (7) |
| where θ=V/Q=hydraulic retention time; Yms is the specific methane production; Q is the flow rate; V is the working volume of the digester. |
| Rate-limiting approaches |
| Construction of the aforementioned AD process kinetic models was generally based in literature on a rate-limiting approach. As previously explained in the introduction, AD involves four critical biological and chemical steps (hydrolysis, acidogenesis, acetogenesis, and methnogenesis) comprised of a sequence of reactions. Initial efforts to simulate dynamic AD processes relied on the assumption that one step was normally much slower than the rest and that a whole process could be adequately described by this step. This last slow step can be referred to as a rate-limiting, rate-controlling, or rate-determining step. The rate-limiting step of AD processes has also been assumed to depend on the temperature, substrate concentration and properties, as well as reactor configuration and loading rate [49]. For example, CH4 generation using organic substrates in tundra soil samples was simulated over a wide temperature range. Hydrolysis and acetoclastic methanogenesis were determined to be the rate-limiting steps between 10–28°C and at 6°C, respectively [50]. |
| Hydrolysis: Most AD rate-limiting models focused on the ratelimiting hydrolysis of complex organic particulate material like sewage sludge [51]. Particulate organic material must be decomposed to solutes capable of being actively or passively transported across cell membranes before they can be microbially metabolized. There are two mechanisms to describe the hydrolytic process [13]: |
| 1. The microbes secrete into the bulk liquid enzymes that adsorb onto a particle or react with a soluble substrate [52]. |
| 2. The microbes adhere to a particle and consume soluble products released by reactions that were catalyzed by enzymes that they locally produced [53]. |
| The following is a list of the hydrolysis kinetics models that were previously reviewed in literature [51]: |
| 1. The first order kinetics of lipid, protein, and carbohydrate degradation: The most conventional model to simulate hydrolysis involves a 1st364 -order rate law in terms of the degradable organic material concentration [51]: |
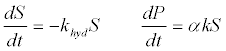 (8) (8) |
| Where P is the product concentration; S is the volatile solids (VS) concentration; khyd is the first order coefficient; and α is the VS-toproduct conversion coefficient;. The kinetic coefficients of the 1st order rate of hydrolysis for different substrates can be obtained from literature [51]. First-order kinetics disregards biodegradability-related processes and applies only when the rate-limitation is due to the particulate substrate surface. |
| 2. Disintegration, solubilisation, and enzymatic hydrolysis: Hydrolysis of a soluble substrate can be described by Michaelis- Menten kinetics as follows [13]: |
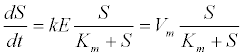 (9) (9) |
| where S is the substrate concentration; E is the enzyme concentration; Vm=kE is the maximum hydrolysis rate; k is the maximum hydrolysis rate constant; and Km is the half-saturation rate coefficient. |
| 3. Biodegradability of complex substrates: A non-degradable fraction of a complex substrate was additionally included to account for substrate non-degradeability in the 1st-order kinetics [51]: |
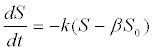 (10) (10) |
| Where S0 is the initial substrate concentration and β is the nondegradable fraction of the substrate. |
| As an alternative to Equation (8), different reaction kinetics can be used to express complex substrate hydrolysis [51]: |
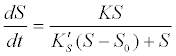 (11) (11) |
| where K is the maximum hydrolysis rate which is a function of the hydrolytic enzyme or biomass or concentration, and K′S is a corresponding model coefficient. |
| Equation (8) also can be modified as nth-order reaction kinetics [51]: |
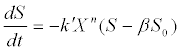 (12) (12) |
| where X is biomass concentration; k’ is a rate constant; and n is a power index. |
| 4. Surface-related kinetics and two-phase model of hydrolysis of particulate substrate: A surface-related hydrolysis-limited kinetic model that considers colonization of waste particles by hydrolytic bacteria is represented by the following [53]: |
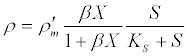 (13) (13) |
| where ρ and ρ’m are the current and maximum hydrolysis rates, respectively; S is the volatile solid waste concentration; X is the concentration of hydrolytic (acidogenic) biomass; β is the equilibrium constant that is equal to the adsorption: desorption rate constant ratio in the Langmuir function; and KS is the half saturation coefficient for the volatile solid waste concentration. In addition, microorganisms that have adhered to a particle will be able to consume soluble products released by the reactions catalyzed by the enzymes that they locally produced. Substrate and biomass saturation kinetics are accounted for by a single parameter in the following Contois model [53]: |
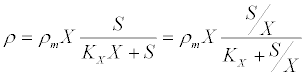 (14) (14) |
| where ρm is the specific maximum hydrolysis ratesand KX is the half saturation coefficient for the substrate: biomass concentration ratio S/X. The differential equations describing the dynamic change in time of substrate, biomass, and product concentrations are as follows [53]: |
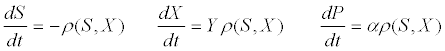 (15) (15) |
| Acetogenesis and Methanogenesis: The formulas pertaining to rate-limiting hydrolysis can be analogously applied to acetogenesis and methanogenesis when these processes are instead considered rate limiting steps, especially for AD involving complex substrates at a high organic loading [51] Occuring after hydrolysis, acidogenesis is normally the most rapid step during AD of complex organic material [40,51]. An acetogenesis rate-limited kinetic model was developed [54]. Here, after 165°C treatment with electric heater, the results of AD processing of complex, waste, activated sludge substrate having an organic loading of 0.5 g COD/g VS of inoculum revealed that acetate and propionate degradation steps could also be viewed as rate-limiting steps [54]. |
| Modeling efforts often view methanogenesis as the rate-limiting step because methanogenic bacteria have the highest sensitivity and lowest growth rates compared to those in the nonmethanogenic groups [5,55]. When substrates were overloaded in one digester, high VFA product concentrations inhibited polymer hydrolysis and acidogenesis and resulted in methanogenesis, as opposed to hydrolysis, becoming the overall AD rate-limiting step [56]. The Andrews ratelimited kinetic model (see Equation 6 (n=1)) disregarded hydrolysis and acidification as rate-limiting and also assumed only a rate-limiting acetoclastic methanogenesis reaction step where CH4 was produced from acetic acid [10]. The Andrews model dynamically simulated the change in biomass of an assumed single bacterial population and acetic acid substrate via mass balances for an assumed continuous stirred tank reactor (CSTR). The Andrews model assumed a constant pH. Mass transfer considerations were limited to the transport of CO2 across the gas-liquid interface, and the dissolved CO2 fraction of total CO2 was estimated by bicarbonate dissociation equilibrium and ion charge balances. In another study, at different operational modes, methanogenesis was also demonstrated to be rate-limiting in the Accumulation System (AC) system, while hydrolysis was rate-limiting during batch digestion [57]. Readily hydrolyzed carbohydrate was pulsed in to ensure that acetogenesis and methanogenesis were ratelimiting, [58]. |
| Other researchers have also viewed the acetoclastic methanogenic process as rate-limiting step [10]. For example, a specific growth rate assuming Monod kinetics with substrate inhibition was expressed as follows: |
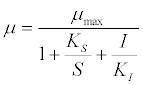 (16) (16) |
| where μ is the specific growth rate; μmax is the maximum specific growth rate; KS is the half saturation coefficient; KI is the inhibition constant; S is the concentration of growth-limiting substrate; I is the inhibitor concentration. |
| This model has served as template for many others, even though it has never been experimentally validated. The arduous task of determining kinetic data to describe the anaerobic acetate-to-methane conversion has frustrated the implementation of this model. Variability in the obtained maximum growth rates still occurred in experiments involving identical cultures of Methanosarcina barkeri, strain 227, and the substrate acetate [59]. This might be the reason why there were fewer rate-limiting model studies in methanogenesis than that in hydrolysis. The rate-limiting model assumption that biogas generation rate can be predicted by one single process step during the fermentation process leads to simple and readily usable models [60]. |
| However, the rate-limiting model may at times over-simplify in that the limiting step is influenced by operating conditions that change with time and are difficult to keep constant. Intermediates fermentation products like volatile fatty acids (VFA), which can be used as indicators for digester stability, become difficult to estimate when only a ratelimiting step (e.g. hydrolysis) or single bacterial organism (e.g., acetoclastic methanogens) are accounted for. |
| Anaerobic Digestion Reactors |
| Different reactor types are used in the AD system. The vertical continuously stirred tank fermenter is the most conventional reactor set-up used for wet fermentation and is implemented in Germany in approximately 90% of its modern biogas plants [21,61]. However, it is becoming apparent that in many applications the common stirred tank is not the optimum AD configuration. Limitation of this reactor include wash-out of unreacted solids and active microorganisms at higher loadings, difficulty in achieving complete mixing, high energy requirements associated with mixing, and disruption of microbial consortia by mixing. Batch and plug flow reactors are common configurations that can alternatively be applied in AD systems. Several innovative digester configurations currently under development aim to increase process stability and net energy output, simplify design and operation, and improve economics. These digesters include the upflow anaerobic sludge blanket (UASB), the attached film, the leach bed, the membrane bioreactor (MBR) and the fluidized bed [62-65]. |
| Black Box Models to Simulate Anaerobic Digesters |
| The complex biological AD process of digesters which involves decomposition by several important microbial populations, is still regarded as a “black-box” because the great efforts in the past that were devoted towards understanding and controlling it have still not led to the development of reliable nonlinear mathematical models [66]. |
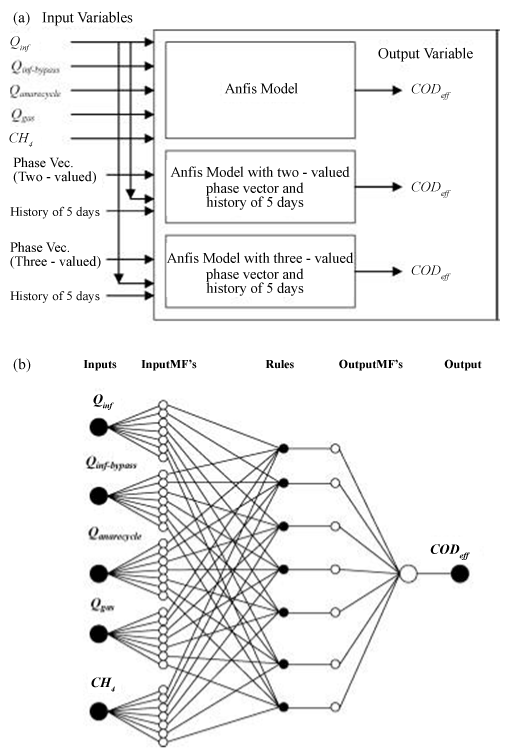
| Unlike nonlinear estimation approaches, artificial neural networks advantageously do not need previous knowledge concerning the interrelationships between key variables. Specification of the network architecture and an adequate amount of consistent input data are all that is required. In one previous instance (Figure 4) [67], the neural network consisted of five critical parts; inputs and outputs, database and pre-processor, fuzzy system generator, fuzzy inference system, and an adaptive neural network representing the fuzzy system. Input and output variables were chosen or formulated from those that are routinely used to define the AD system. The model relied on a database that includes system performance data that is usually collected from regularly monitored variables. |
| Currently available soft-computation artificial neural networks techniques which do not need to consider mechanistic reactions can be applied to biological wastewater treatment processes [68-73]. For example, effluent that originated from municipal sewers or other residential areas was defined by only the four input effluent properties [74]. These were Suspended Solids (SS), Biochemical Oxygen Demand (BOD), Chemical Oxygen Demand (COD), and true effluent color. Such inputs were processed at a wastewater treatment plant to achieve the necessary outputs stipulated by the regulatory effluent standards. Compared to other more comprehensive studies, this particularly sparse and incomplete study of the output effluent quality was, to save money, conducted only to comply with the regulatory standards and did not appropriately predict long-term effluent quality trends via numerical models involving mechanisms, etc. models. |
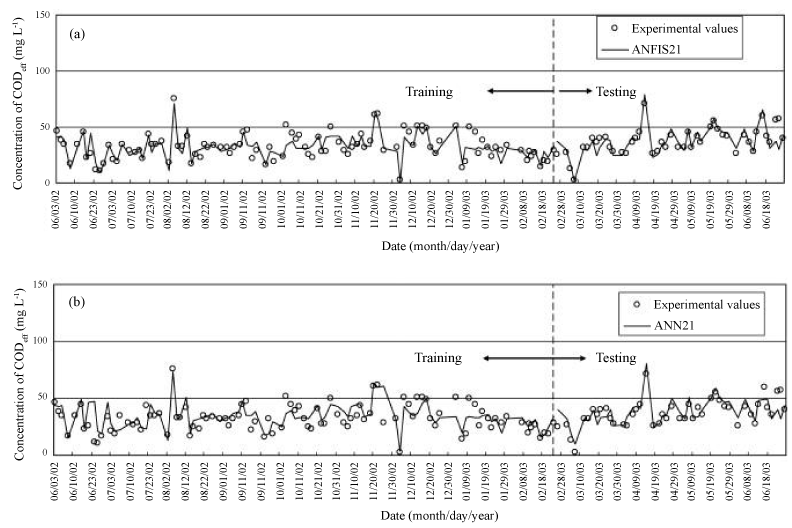
| In another example, two training algorithms (Artificial Neural Network (ANN) and adaptive neuro fuzzy inference system (ANFIS)) were applied to predict chemical oxygen demand (CODeff) and suspended solids (SSeff) in effluent from a hospital wastewater treatment plant. ANFIS’s platform was composed of both ANN and fuzzy-logic including if–then rules and linguistic expression of Membership Functions (MFs). Its predictive power was high based on Mean Absolute Percentage Error (MAPE), correlation coefficient (R), Mean Square Error (MSE), and Root Mean Square Error (RMSE) values. The training results and predictions using ANFIS2-1 and ANN2-1are presented in Figure 5a and b, respectively. |
| Phenomenological models for simulating anaerobic digesters |
| Ideal Models (CSTR and PFR): Model equations have been constructed for various reactor configurations, most commonly Continuous Stirred Tank Reactor (CSTR) and Plug Flow Reactor (PFR), from fundamental kinetics and biomass mass balance relationships. Angelidaki’s comprehensive model [12] and ADM1 model [13] assumed CSTR reactor configurations, reducing the computational requirements when considering the complex AD kinetics. CSTR mixing intensity was also evaluated via a distributed model that was developed to simulate anaerobic digestion of solid waste by exploring the balance between the rates of polymer hydrolysis and methanogenesis during the anaerobic conversion of rich and lean wastes in batch and continuous-flow reactors [14,56,75]. |
| Mathematical models for Anaerobic Fluidized Bed Bioreactors (AFBR) were developed specifically as CSTR [76], plug-flow reactor [77] and a plug flow with dispersion reactor configurations [78]. AFBR models assumed the CSTR’s lack of axial spatial gradients in substrate and product concentrations because of their traditionally highrecirculation rates. However, biofilm thickness and heterogeneity could increase, and colonized media density could significantly decrease during continuous operation. This may result in large decreases in AFBR recycle ratio or changes in bed characteristics, invalidating the CSTR model assumption. Therefore, numerous models for fluidized bed reactors involving a plug-flow regime with axial dispersion were developed to account for substrate and product concentration gradients in AFBRs [79]. |
| Other high-rate digester models were also developed [80], including, for example, a dynamic model for the anaerobic digestion of glucose in the Periodic Anaerobic Baffled Reactor (PAFB) [81]. This model assumed that a four-compartment PABR was hydraulically equivalent to four CSTRs in series. In another model, an anaerobic moving bed reactor was simulated by constructing a material balance within the biofilm, incorporating a flow rate term into a Monod growth kinetic equation, and applying Fick’s law of molecular diffusion [82]. Furthermore, a leach-bed reactor, made from compacted municipal solid waste (MSW), and comprising large and small pores, was simulated by coupling a moisture-flow model with a biological reaction and a physico-chemical equilibrium model [83]. The nonuniform water flow through the heterogeneous leach bed was instead considered high-velocity channeled flow of leachate through narrow pore channels and inter- and intra-particle Darcian flow percolating through small pores. |
| Non-ideal models: Various reactor models for high rate anaerobic digesters were constructed by combining properties of both CSTR and PFR configurations to account for non-idealities. For instance, the different zones of a UASB reactor have been viewed as CSTRs or PFRs with dead volumes and bypass flows between them. The zone flows primarily were affected by biomass concentration and properties. In one study, a UASB reactor was split into the three compartments of sludge bed, sludge blanket, and settler [84]. CSTR liquid flow in the sludge bed and the sludge blanket compartments and PFR liquid flow in the internal settler were assumed. In another case, a UASB reactor’s sludge bed and blanket were hydrodynamically modeled as a nonideal CSTR in series by combining an ideal CSTR configuration with a dead zone and a bypass flow. Meanwhile, the UASB’s settler above the sludge blanket was hydrodynamically modeled as a dispersed plug flow reactor (PFR) (non-ideal PFR) [85]. Additionally, the UASB was split into two regions with ideal mixers, and a recirculation tank was viewed as a third ideal 551 mixer because numerous hydrodynamic studies previously determined that the sludge bed and sludge blanket were definable as separate, well-mixed flow regions [86]. |
| CSTR and PFR models have been extensively applied to the design, scale-up, and optimization of commercial reactors. Non-idealities were considered via a multitude of modifications, including tanks-inseries and axial-dispersion models. However, these did not adequately simulate reactor performance, which was influenced not only by vessel residence time for a fluid element, but also by its surroundings when transported from inlet to outlet [87]. Quantitative data regarding digester flow pattern were required for sufficient designs so that the effective mixing strategies can be operated to avoid recirculation (backmixing), short circuits, and dead zones. |
| Computational Fluid Dynamics (CFD) Models: Mixing can promote optimum digester performance by enhancing intimate contact between active microorganisms and feed sludge substrates [88]. Computational fluid dynamics (CFD) simulation software allows numerical simulation of mixing effect in a digester [89]. CFD can be used also to predict anaerobic digester velocity profiles, rates of energy dissipation, concentrations, and flow streamlines based on specified digester geometry, feed location, physical properties, and operating conditions. In the past decade, CFD has been used to predict digester flow patterns of wastewater treatment units like wastewater ponds, lagoons, and tanks. |
| CFD was first applied to the design of wastewater ponds [90,91]. The single-phase Euler approach and finite volume numerical method were commonly used. For this, the flow field was calculated in four different ponds types-rectangular facultative, inlet baffle, outlet baffle, and aerates. It was determined later that current designs and operating models pay little attention to the micro-scale effects within the treatment ponds. The effects of inlet formation and basin inlet geometry were additionally simulated, and 2-D CFD models qualitatively demonstrated that the waste pond flow fields were most influenced by inlet geometry. Shilton [92] and Shilton et al. [93] sought to complement and extend on such research of Wood et al. [91] by presenting the results of a 3-D, turbulent model. |
| CFD has also been applied to the study of lagoons, another common form of simple digester. Salter et al. [94] focused on the hydraulic regime in facultative lagoons and conducted two consecutive simulations with and without baffles; the first simulation established steady-flow conditions, and the second simulation used a chemical species transport model to get the Residence Time Distribution (RTD). Baleo et al. [95] employed two different numerical approaches to obtain lagoon residence time distributions. The first consisted of solving a transport equation for the local fluid mean age via Eulerian reference frame. The second consisted of injecting a virtual particle stream and measuring the time between start injection and end of trajectory via Lagrangian reference frame. |
| Tanks are relatively small compared with ponds and lagoons. Small size of tank digesters permits the use of a more flexible mixing strategy to ensure effective mass and heat transfer. Wu and Chen [96] accounted for slurry circulation to obtain flow patterns in lab-, pilot-, and commercial-scale digesters and concluded that power input per unit digester volume logarithmically increased for scale-up digesters. Hoffmann et al. [88] used CFD to model mechanical mixing by an A-310 impeller in a low-solid digester (TS<5%) that was processing animal manure. Animal manure was then considered to be a Newtonian fluid with constant viscosity. The simulation of mechanical mixing was further extended to digestion of animal manure with total solids content exceeding TS>10% [97]. If the high-solids digester requires more efficient mixing, mechanical mixing will be the most optimal way to keep substrate in close contact with microorganisms [98]. |
| Despite the efforts to apply the concept of non-Newtonian fluid in single-phase models during CFD simulation [99,100], it is important to note that the very complex flow behavior of mixed liquor or waste slurry in digesters also involves segregation and aggregation phenomena [101]. These may significantly impact the interactions between active microorganisms and feed sludge, the microorganism retention, and, ultimately, biogas productivity. Therefore, multi-phase non-Newtonian models may be necessary to adequately simulate the complex flow behavior of heterogeous biomass particles in AD sludge, as they differ tremendously from flows of smooth spherical particles in Newtonian fluid. Compared to single-phase Newtonian fluid models, multi-phase non-Newtonian fluid models have not been extensively developed. This has likely held back the understanding, optimization, and commercialization of AD processes [102]. Despite their added complexity and challenges, development and application of such models represent a significant opportunity to advance the field of anerobic digestion. |
| Conclusions |
| This review presents a compilation and discussion of the various models that have been developed to describe Anaerobic Digestion (AD) processes so as to optimize and enhance design and operation of waste treatment plants. The relatively simple and implementable rate-limiting models were first highlighted. However, their diversity and customized development for applications involving specific substrates limited their widespread implementation. It was found that identification of rate-limiting steps at different digester conditions was difficult for AD processes involving complex substrates. It was also found that identification of intermediate fermentation products was very important to assess the capability of digesters. |
| ADM1 represents the currently most comprehensive model of the AD process which serves as a basis for future development of kinetics models. Its complex model structure still welcomes additional improvements. For example, understanding further the intra-cellular metabolic pathways, mechanisms, and interactions between anaerobic microorganisms at the micro-scale can lead to an improved model that better represents real-world AD processes. In addition, the ADM1 model can be further modified for a special anaerobic process involving different metabolic pathways. |
| Because of the complex reaction mechanisms in AD, black box models like artificial neural networks were applied to the simulation of wastewater plants. As these models disregarded reaction mechanisms, they would be more suitable to control, rather than design and scaleup, AD processes. CSTR and PFR models provided the fundamental basis for applying kinetics to design different types of digesters. An axial dispersion model was further developed to account for non-idealities. |
| Fluid dynamic studies are needed to provide a better understanding of local transport phenomena inside digesters to improve their design and predict their performance. CFD was applied to the simulation of anaerobic digesters to study the effects of mixing. CFD simulation of AD processes can further be augmented with inclusion of comprehensive kinetics [103], although the extremely complex nature of these would likely limit progress in the near-term. It is essential that researchers developing and conducting in-silico model simulation communicate effectively with those conducting physical experimentation. Doing so would mutually benefit both groups and help advance the field of mathematical modeling in anaerobic digestion. |
| Acknowledgements |
| The authors thank the Washington State Department of Ecology Waste to Fuels program and their funding via contract # C1000172. |
References
|
Tables and Figures at a glance
| Table 1 |
Figures at a glance
 |
 |
 |
 |
 |
| Figure 1 | Figure 2 | Figure 3 | Figure 4 | Figure 5 |
Relevant Topics
- Anaerobic Biodegradation
- Biodegradable Balloons
- Biodegradable Confetti
- Biodegradable Diapers
- Biodegradable Plastics
- Biodegradable Sunscreen
- Biodegradation
- Bioremediation Bacteria
- Bioremediation Oil Spills
- Bioremediation Plants
- Bioremediation Products
- Ex Situ Bioremediation
- Heavy Metal Bioremediation
- In Situ Bioremediation
- Mycoremediation
- Non Biodegradable
- Phytoremediation
- Sewage Water Treatment
- Soil Bioremediation
- Types of Upwelling
- Waste Degredation
- Xenobiotics
Recommended Journals
Article Tools
Article Usage
- Total views: 23441
- [From(publication date):
specialissue-2014 - Aug 29, 2025] - Breakdown by view type
- HTML page views : 17325
- PDF downloads : 6116
