Research Article Open Access
Membrane Bound Molecular Machines for Sensing
William Hoiles*, Vikram Krishnamurthy and Bruce Cornell
PhD Student, The University of British Columbia, Canada
- *Corresponding Author:
- William Hoiles
PhD Student
The University of British Columbia
Vancouver, British Columbia, Canada
Tel: 604-822-5949
E-mail: whoiles@ece.ubc.ca
Received Date: March 26, 2014; Accepted Date: April 28, 2014; Published Date: April 30, 2014
Citation:Hoiles W, Krishnamurthy V, Cornell B (2014) Membrane Bound Molecular Machines for Sensing. J Anal Bioanal Tech S7:014. doi: 10.4172/2155-9872.S7-014
Copyright: © 2014 Hoiles W, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Analytical & Bioanalytical Techniques
Abstract
This paper reports on the construction and predictive models of the Ion Channel Switch (ICS) biosensor which is capable of detecting femto-molar concentrations of target species including proteins, hormones, polypeptides, microorganisms, oligonucleotides, DNA segments, and polymers in cluttered electrolyte environments. The ICS employs an engineered tethered membrane with embedded gramicidin (gA) monomers and tethered antibody receptors. The detection of target molecules using the ICS is performed by measuring changes in the membrane conductance which is dependent on the number of gA dimers. As target molecules bind with the antibody receptors on the membrane surface, the conductance of the membrane decreases as a result of the decrease in the number of conducting gA dimers. As we show, the membrane conductance can be predicted using continuum theories for electrodiffusive flow coupled with boundary conditions for modelling chemical reactions and electrical double layers present at the bioelectronic interface of the ICS. Using the predictive model allows the concentration of analyte and surface reaction rates to be estimated from the current response of the ICS. To validate the predictive accuracy of the dynamic models, experimental measurement of streptavidin and ferritin analyte concentrations are performed using the ICS. Streptavidin is a useful example as the binding of streptavidin to biotin is one the strongest non-covalent bonds known in nature, and detection of the change in the concentration of ferritin can be linked to pathogenic infections or the presence of cancer.
Keywords
Ion Channel Switch (ICS); Streptavidin; Oligonucleotides; DNA segments
Introduction
In this work the construction and dynamic modelling of the Ion Channel Switch (ICS) biosensor is presented. A key feature of the ICS biosensor is that the detection is performed by measuring the timedependent conduction of the engineered tethered membrane which is dependent on the ensemble of aqueous pores and conducting gA dimers present. Using specific molecular components and drive potentials, the ICS can be designed to detect a specific analyte molecules of interest.
Recent advances in detecting biomolecules includes the nanogap biosensor [1,2] and the nanoneedle biosensor [3]. The nanogap biosensor relies on detecting impedance changes of the electrode surface which is proportional to the concentration of target molecules. An issue with the nanogap biosensor and similar sensors is that spurious electrochemical reactions resulting from proteins and ions binding to the electrode surface can interfere with measurements. As the nanogap biosensor utilizes a redox active electrode (e.g. Ag/AgCl) [2], the electrode ablates and releases metal ions into solution which can conformationally change the biomolecules being detected effecting the measurement. The nanoneedle biosensor utilizes the change in conduction between two poly-silica phosphorous doped electrodes sandwiched between silicon dioxide. The electrodes are placed 30 nm apart allowing for the detection of biomolecules. As silicon is poorly soluble it does not release harmful ions into solution; however, since silicon dioxide has an isoelectronic point of 3, the adsorption of certain proteins and peptides on the surface is a possibility [3]. Given the electrode size and detection mechanism of the nanoneedle biosensor it is difficult to perform concentration estimates of target species of interest in cluttered electrolyte environments.
To overcome these limitations, the ICS biosensor employs an inert bioelectronic interface and an engineered tethered membrane for detection and measurement. The electrical instrumentation of the ICS is connected to the electrolyte solution via gold electrodes. Using gold electrodes as the bioelectronic interface provides a superior interface as compared with redox active electrodes for two reasons [4]. First, if redox active electrodes are used, the metal will ablate causing the tethers to dissociate from the electrode surface destroying the membrane. Second, redox active electrodes release metal ions into solution which can interfere with the electrophysiological response of proteins and peptides. The inert gold electrode capacitively couples the electronic domain to the physiological domain without the issues associated with redox electrodes, however the capacitive effects of the electrode must be accounted for when modelling the ICS biosensor.
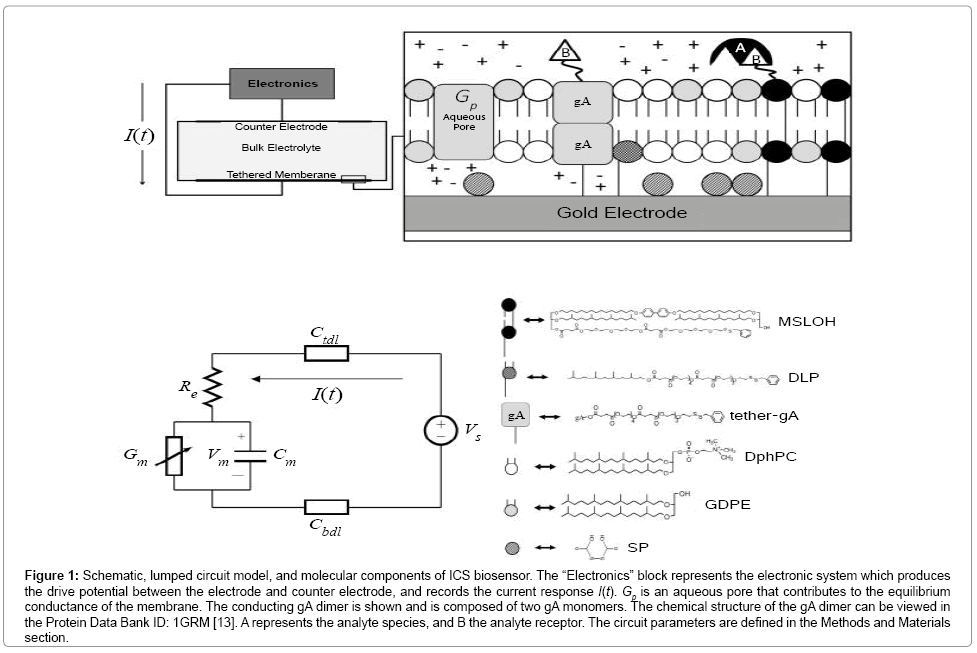
A schematic of the ICS is given in Figure 1. Useful for experimentalists is the fact the ICS can be designed with specific binding cites with the membrane having a lifetime of several months [4-9]. The engineered tethered membrane is composed of a self-assembled monolayer of mobile lipids and gA monomers, and a self-assembled monolayer mobile lipids and gA monomers. The tethered components are anchored to the gold electrode via polyethylene glycol chains. Spacer molecules are used to ensure the tethers are evenly spread over the gold electrode. The intrinsic spacing between tethers and spacers is maintained by the benzyl disulfide moieties which bond the spacers and tethers to the electrode surface. A time-dependent voltage potential is applied between the electrodes to induce a transmembrane potential of electrophysiological interest; this results in a current I(t) related to the charging of the double-layers and the conductance of the engineered tethered membrane.
Figure 1: Schematic, lumped circuit model, and molecular components of ICS biosensor. The “Electronics” block represents the electronic system which produces the drive potential between the electrode and counter electrode, and records the current response I(t). Gp is an aqueous pore that contributes to the equilibrium conductance of the membrane. The conducting gA dimer is shown and is composed of two gA monomers. The chemical structure of the gA dimer can be viewed in the Protein Data Bank ID: 1GRM [13]. A represents the analyte species, and B the analyte receptor. The circuit parameters are defined in the Methods and Materials section.
The ICS biosensor is capable of detecting femto-molar concentrations of target species including proteins, hormones, polypeptides, microorganisms, oligonucleotides, DNA segments, and polymers in cluttered electrolyte environments [10-12]. This remarkable detection ability is achieved using engineered receptor cites connected to mobile gA monomers and biotinylated lipids in the tethered membrane, refer to Figure 1. By measuring the dynamics of the membrane conductance, the concentration of a specific analyte can be estimated. In reference to Figure 1, the mobile gA monomer is tethered to a biological receptor such as a nucleotide or antibody which binds to specific target species. In the neighbourhood of the mobile gA, a tethered monolayer lipid is present with the tethered receptor present in contact with the analyte solution. When the receptor binds to the analyte, the mobile gA monomer diffuses to the tethered lipid causing the conducting gA dimer to break. As an ensemble of gA dimers dissociate, the conductance of the membrane decreases. Measurement of the conductance change allows both the detection of the analyte species and a estimate of the concentration of the analyte species in cluttered environments as the receptor is designed to bind to a specific target species. To relate the analyte concentration to changes in membrane conductance requires the use of an electrodiffusive model for the analyte coupled with the surface reactions present at the tethered membrane surface. In the Materials and Methods section, we have constructed dynamic models for estimating the analyte concentration and surface reaction rates at the tethered membrane surface for estimating the analyte concentration.
To illustrate the application of the ICS, we compare the predicted membrane conductance with experimentally measured membrane conductance for the analyte species streptavidin [14] and ferritin [15]. Streptavidin provides a useful example as the binding affinity for streptavidin to biotin is extraordinarily high [16]. Analyte concentrations of 1000 pM, 100 pM, and 10 pM of streptavidin are used for experimental validation of the dynamic models presented. Streptavidin has a molecular weight of 52.8 kDa; to illustrate the detection characteristics of the ICS for larger molecules we consider ferritin which has a molecular weight of 450 kDa. Ferritin plays a central role in the transport, storage, and release of iron. It is known that ferritin concentrations increase drastically in organisms with pathogenic infections or cancer. Therefore, the ability to detect such an event is helpful for rapid point-of-care diagnostics useful for patient healthcare. We consider the detection of 200 pM, 400 pM, and 600 pM concentrations of ferritin using experimental measurements from the ICS.
The paper proceeds by presenting how the ICS sensor is constructed, dynamic models, and parameter estimation in the Methods and Materials section. The Results and Discussion section illustrates the predictive accuracy of the dynamic models developed in the Methods and Materials section for the experimental measurement of streptavidin and ferritin. Closing remarks are provided in the Conclusion section.
Materials and Methods
In this section the formation and predictive models of the ICS biosensor are presented. Note that the models presented in this section can be considered as extensions to the models presented for the BIACORE surface plasmon resonance optical system and sandwich assay lateral flow bio-reactors [17-19].
Ion channel switch biosensor construction
The construction and formation of the ICS biosensor can be found in [7,20,21], for completeness the experimental setup of the ICS is presented below.
The ICS is supported by a 1×25×75 mm polycarbonate slide onto which is patterned a 100 nm vacuum magnetron sputtered gold electrode array possessing six 0.7×3 mm active areas of membrane each of which is enclosed in a flow cell with a common gold return electrode. The sputtered gold surface is immersed in an ethanol solution containing the tethering species comprised of tethered gA monomers (tether-gA), membrane spanning lipids (MSLOH), biotinylated membrane spanning lipid (MSLB), and half membrane spanning lipids (DLP). The chemical structures of tether-gA, MSLOH, MSLB and DLP are given in Figure 1. The gold surface is immersed in the tethering solution for a period of 10 min. Following an alcohol rinse, 5 μL of ethanol solution containing mobile lipids (GDPE, DphPC) and gA monomer components are added to construct the self-assembled mobile layer of the ICS. The untethered biotinylated gA monomers contain biotin linked via a 5-aminocaproyl linker to the gA monomer. Note that the biotinylated antibody can be designed to detect a host of analytes, here we have selected biotin as we are sensing the presence of the analyte streptavidin. For the detection of ferritin, a biotinylated antibody is bound to ferritin, which then binds to streptavidinbiotinylated tethered lipids and gA monomers. The salt concentration of the electrolyte solution in the ICS after formation is 0.15 M.
The quality of the ICS and experimental measurements are made continuously using an SDx tethered membranes tethaPodTM swept frequency impedance reader operating at frequencies of 1000, 500, 200, 100, 40, 20, 10, 5, 2, 1, 0.5, 0.1 Hz and an excitation potential of 20 mV (SDx Tethered Membranes, Roseville, Sydney). The membrane was equilibrated for 30 min prior to measurements. Typically a tethered archaebacterial membrane containing no ion channels has a conductance of approximately 1 μS for a 0.7 mm×3 mm membrane surface. The conductance of gA dimers is in the range of 0.8-2.0 pS [22,23]. Given the experimenter can control the number of gA dimers present in the membrane, after equilibration of the membrane conductance is significantly varies from the expected result then an error in the formation process has occurred. Additionally, if the measured impedance varies significantly from the lumped circuit model presented in the Materials and Methods section, this suggests the presence of membrane defects invalidating any concentration estimates from the ICS.
Estimating the membrane conductance from current measurements
In this section we present an equivalent circuit model of the ICS biosensorthat is used to estimate the time dependent conductance Gm(t), illustrated in Figure 1. Estimation of Gm(t) is vital for the functionality of the ICS with this section providing the basis for the measurement of the analyte concentration, formally presented in the Ion Channel-Switch Biosensor Dynamic Model section.
The ICS is composed of three distinct regions: the bioelectronic interface at the gold electrodes, the tethered membrane, and the bulk electrolyte solution. The tethered membrane is assumed to be uniformly polarizable such that the charging dynamics at the surface of the membrane can be modelled by a capacitance Cm. The membrane also conducts ions; this effect is accounted for with a tethered membrane conductance Gm(t,Vm) in parallel with the membrane capacitance Cm. Note that Gm(t,Vm) is both time and membrane voltage dependent with Vm denoting the transmembrane potential. The dependency of Gm is a result of the number of conducting gA dimers and aqueous pores present in the membrane. The bulk electrolyte solution is assumed to be purely ohmic with a resistance Re. We denote Ctdl and Cbdl as modelling the bioelectronic interface. The excitation potential Vs(t) applied across the two electrodes closes the circuit. The equivalent circuit model of the tethered membrane platform is given in Figure 1 and has been extensively used to model the electrophysiological response of tethered membrane platforms [5,8,24-26].
The diffusion process present at the bioelectronic interface plays a central role in the selected models Ctdl and Cbdl. The bioelectronic interface contains a tightly bound region of ions on the order of an atomic radii, and a diffuse region with a length on the order of the Debye-Hückel thickness. These two regions are commonly referred to as the Stern and diffuse charge layers. If ions in proximity to the bioelectronic interface satisfy a pure diffusion law (i.e. the mean squared displacement of a particle is a linear function of time <x2>∝Dt), then the Stern and diffuse charge layers can be modelling by an equivalent capacitance Ctdl, and Cbdl for the counter electrode and electrode respectively. As a result of the spacers used in the ICS, it is likely that the diffusion in the neighbourhood of the bioelectronic interface satisfies the subdiffusion process such that <x2>∝tα. The detection of this subdiffusion process is well known for solid electrode to electrolyte interfaces and can be detected by measuring the frequency response of the interface, refer to [5,27]. If the interface satisfies a constantphase- element (CPE) model, then subdiffusion is present suggesting that electrode effects from surface roughness, electrode porosity, and electrode geometry are non-negligible. In the time-domain, fractional calculus is used to represent the current-voltage relationship of the bioelectronic interface [28,29] (Table 1).
| Symbol | Definition | Value |
|---|---|---|
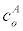 |
inlet analyte concentration | 1-1000 pM |
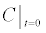 |
mobile gA monomers | 109 molecules/cm2 |
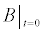 |
tethered binding sites | 1010 molecules/cm2 |
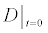 |
gA dimers | 109 molecules/cm2 |
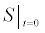 |
tethered gA monomers | 1010 molecules/cm2 |
| W, X ,Y, Z | initial concentration | 0 molecules/cm2 |
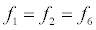 |
forward reaction rate | 4×106 M-1s-1 |
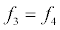 |
forward reaction rate | 5-9 cm2s-1 molecules-1 |
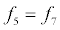 |
forward reaction rate | 10-10 cm2s-1 molecules-1 |
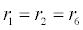 |
reverse reaction rate | 10-6s-1 |
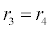 |
reverse reaction rate | 10-6 s-1 |
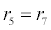 |
reverse reaction rate | 1.5×10-2 s-1 |
| DA | Diffusivity of analyte A | 10-6 cm2/s |
| LW | Width of flow chamber | 3.0 mm |
| L | Length of flow chamber | 0.7 mm |
| h | Height of flow chamber | 100 µm |
| Q | Flow Rate | 100 µL/min |
Table 1: Model Parameters for ICS Detection of Streptavidin.
The governing equations of the tethered membrane system are given by:
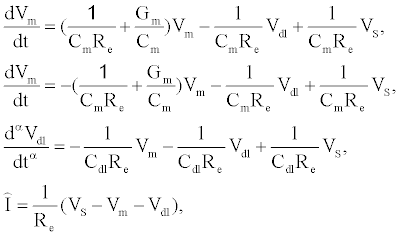 (1)
(1)
where 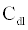 is the total capacitance of tdl
is the total capacitance of tdl 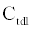 C and bdl C
C and bdl C 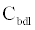 in series, α is the anomalous diffusion parameter in the range of 0<α≤1. Note if α=1 then standard diffusion applies at the bioelectronic interface. Given
in series, α is the anomalous diffusion parameter in the range of 0<α≤1. Note if α=1 then standard diffusion applies at the bioelectronic interface. Given 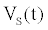 , and the static circuit parameters
, and the static circuit parameters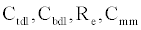 and diffusion parameter α, the membrane conductance
and diffusion parameter α, the membrane conductance 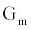 can be estimated from the measured current I(t).
can be estimated from the measured current I(t).
Using (1) with the measured current I(t) to estimate Gm is computationally prohibitive for arbitrary waveforms as a result of the fractional order differential operator in (1). If the electrodiffusive properties of the analyte are not of interest to the experimentalist, or if the analyte is uncharged then the drive potential 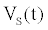 can be engineered to allow straightforward estimation of
can be engineered to allow straightforward estimation of 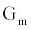 . If a sinusoidal drive potential
. If a sinusoidal drive potential 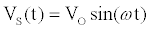 with radial frequency
with radial frequency 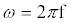 and magnitude
and magnitude 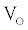 is applied, the computation of I can be done using a set of algebraic equations. Using the sinusoidal drive potential and converting (1) into the complex domain using the Laplace transform, the current is given by
is applied, the computation of I can be done using a set of algebraic equations. Using the sinusoidal drive potential and converting (1) into the complex domain using the Laplace transform, the current is given by 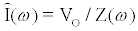
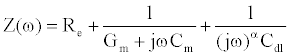 (2)
(2)
In (2), j denotes the complex number 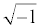 . Using the Laplace transform the measured current I(t) is converted into the complex domain, and
. Using the Laplace transform the measured current I(t) is converted into the complex domain, and 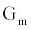 is estimated using a least-squares method to reduce the error given by (
is estimated using a least-squares method to reduce the error given by (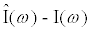 )
)
Ion channel-switch biosensor dynamic model
In this section we present a model for the electrodiffusive flow of analyte molecules in the ICS, and link the electrodiffusive properties of the analyte to the number of conducting gA dimers in the ICS. Given the number of gA dimers effects the measured membrane conductance, this allows estimation of the analyte concentration and surface reaction rates of the ICS.
For charged analyte molecules, the Poisson-Nernst-Planck (PNP) system of equations derived from statistical mechanics assuming all electrolyte ions are point-like are classically used [30]. If the analyte molecules are not suitably point like, then the PNP system equations can not be used. This can occur if the analyte molecules are sufficiently large such that steric effects at the surface of the ICS are non-negligible as analyte molecules in the neighbourhood of the surface prevent the diffusion of analytes in the bulk electrolyte from reaching the surface. Using statistical mechanics, the free energy of an electrolyte solution can be estimated with steric effects of analyte molecules included using a “Langmuir type” activity coefficient [31]. The chemical potential of the electrolyte is computed by taking the ratio of the change in free energy and change in species concentration. Given the chemical potential of the electrolyte, partial differential equations (PDEs) governing the electrolyte dynamics can be derived as outline in [32]. The results of this derivation are denoted as the Generalized PNP (GPNP) and are given by [33]:
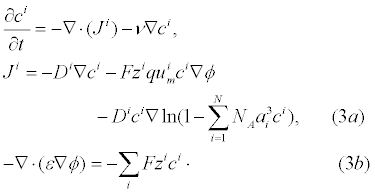
In (3a), Ji is the concentration flux, 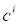 is the concentration of the analytes present, φ is the electrical potential,
is the concentration of the analytes present, φ is the electrical potential, 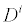 is the diffusivity, NA is Avagadro’s number, ai is the effective ion size,
is the diffusivity, NA is Avagadro’s number, ai is the effective ion size,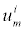 is the ionic mobility with i denoting the analyte species, and v is the velocity field. In (3b), F is Faraday’s constant where the superscript defines the chemical species i, q is the elementary charge,
is the ionic mobility with i denoting the analyte species, and v is the velocity field. In (3b), F is Faraday’s constant where the superscript defines the chemical species i, q is the elementary charge, 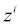 is the charge valency, and ε is the electrical permittivity. The electrodiffusive model (3) is able to account for asymmetric electrolytes and multiple charged analyte species. Note that for
is the charge valency, and ε is the electrical permittivity. The electrodiffusive model (3) is able to account for asymmetric electrolytes and multiple charged analyte species. Note that for 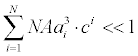 , the steric effects are negligible in (3) and the standard PNP formulation can be used to model the electrolyte dynamics.
, the steric effects are negligible in (3) and the standard PNP formulation can be used to model the electrolyte dynamics.
To relate the population of dimers D(t) to the analyte dynamics (3), we use a reaction boundary condition ∂Ωsurf at the surface of the membrane in contact with the electrolyte. On ∂Ωsurf analyte molecules bind to the tethered antibody sites followed by a cross-linking of the mobile gA monomers to the captured analytes. The primary species involved in this process include the analytes a, binding sites b, mobile gA monomers c, tethered gA monomers s, and the dimers d, with respective concentrations {A,B,C,S,D}. Other chemical complexes present include w,x,y,andz with concentrations {W,X,Y,Z}. The chemical reactions that relate these chemical species are described by the following set of reactions [10-12]:
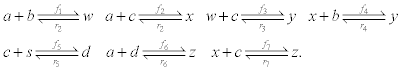 (4)
(4)
In (4), ri and fi, for ε{1,2,3,4,5,6,7}, denote the reverse and forward reaction rates for the chemical species {a,b,c,d,s,w,x,y,z}. An explanation of the reactions that take place can be found in [12].
The surface reactions (4) can be enforced on the governing equations (3) using a flux boundary condition. For uncharged zi=0 and analytes with negligible steric interaction ai=0, the governing equations (3) reduce to a standard advection-diffusion PDE. The boundary conditions of the advection-diffusion PDE are given by:
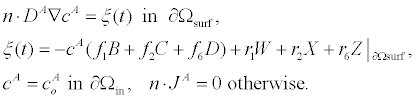 (5)
(5)
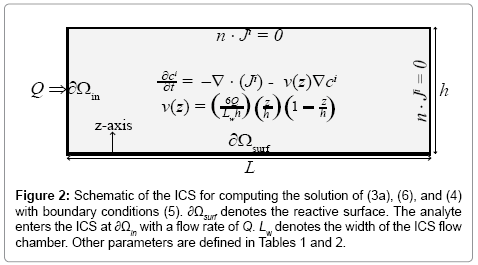
In (5), Ao is the analyte concentration at the inlet, and ξ(t) is the surface flux of analyte species c^A resulting from the chemical reactions (4). Given the time-scale of the conductance measurements is seconds, we assume that the velocity field v is a fully developed laminar flow with a parabolic velocity profile given by:
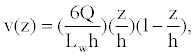 (6)
(6)
where Q,W, and h are defined in Figure 2 and Table 2.
| Symbol | Definition | Value |
|---|---|---|
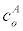 |
inlet analyte concentration | 200-600 pM |
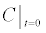 |
mobile gA monomers | 2×109 molecules/cm2 |
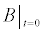 |
tethered binding sites | 1×1010 molecules/cm2 |
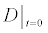 |
gA dimers | 109 molecules/cm2 |
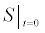 |
tethered gA monomers | 1×1010 molecules/cm2 |
| W, X ,Y, Z | initial concentration | 0 molecules/cm2 |
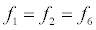 |
forward reaction rate | 8 × 106 M-1 s-1 |
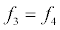 |
forward reaction rate | 5-9 cm2 s-1 molecules-1 |
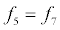 |
forward reaction rate | 10-10 cm2s-1 molecules-1 |
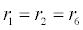 |
reverse reaction rate | 10-6 s-1 |
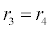 |
reverse reaction rate | 10-6s-1 |
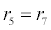 |
reverse reaction rate | 1.5 × 10-2 s-1 |
| DA | Diffusivity of analyte A | 2.5 ×10-6 cm2/s |
| LW | Width of flow chamber | 3.0 mm |
| L | Length of flow chamber | 0.7 mm |
| h | Height of flow chamber | 100 µm |
| Q | Flow Rate | 10 µL/min |
Table 2: Model Parameters for ICS Detection of Ferritin.
Using (3a), (6), and (4) with boundary conditions (5) we can estimate the population of gA dimers D(t) given Q,DA, and the reaction rates in (4). The estimated membrane conductance Gm is a combination of the equilibrium conductance of the membrane GO from aqueous pores, and the conductance from the population of gA dimers 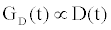 , where
, where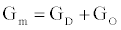 is the number of gA dimers. Given
is the number of gA dimers. Given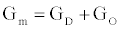 and
and 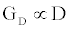 , the measured change in membrane conductance can be related to the analyte concentration Ao, and the reaction rates in (4) simultaneously estimated.
, the measured change in membrane conductance can be related to the analyte concentration Ao, and the reaction rates in (4) simultaneously estimated.
Computing model parameters using maximum likelihood estimator
How can we estimate the reaction rates in (4) given the time-dependent conductance of the ICS biosensor. From (3) and (5) we can estimate the conductance given the parameters 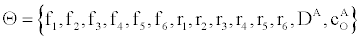 with the flow rate Q and initial conditions known. The membrane conductance satisfies
with the flow rate Q and initial conditions known. The membrane conductance satisfies 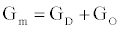 with
with 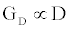 . Therefore we can compute the time dependent conductance of the membrane using (3) and (5), given by:
. Therefore we can compute the time dependent conductance of the membrane using (3) and (5), given by:
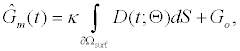 (7)
(7)
Where 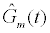 is the estimated conductance, and κ is the proportionality constant relating the conductance of the gA dimers to the number of gA dimers. From the experimental measurements we have a finite number of conductance measurements given by { } m m 1 m 2 m K G = G (T ),G (T ),...,G (T )
is the estimated conductance, and κ is the proportionality constant relating the conductance of the gA dimers to the number of gA dimers. From the experimental measurements we have a finite number of conductance measurements given by { } m m 1 m 2 m K G = G (T ),G (T ),...,G (T ) 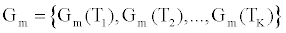 . The estimation of the model parameters in the least-squares sense requires the solution of the following constrained optimization problem:
. The estimation of the model parameters in the least-squares sense requires the solution of the following constrained optimization problem:
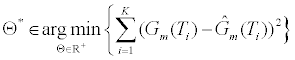 (8)
(8)
In Θ* (8), the parameter Θ* denotes the solution to the constrained optimization problem. The parameter D(t;Θ) is computed using (3) and (5) using the parameters in Θ. To estimate Θ* we utilize the “Levenberg- Marquardt” algorithm. Given the conductance measurements of the ICS are corrupted by independent stationary white Gaussian noise, this nonlinear least squares method provides the maximum likelihood estimate of the parameters of the model parameters Θ.
Numerical methods
The governing equations (3a) and (6) with boundary condition (5) are solved numerically with the commercially available finite element solver COMSOL 4.3a (Comsol Multiphysics, Burlington, MA). To solve the advection-diffusion (3a) and (6) the COMSOL modules Transport of Diluted Species, and to solve the distributed system of nonlinear ODEs (4) the Weak Form Boundary PDE module is used. The “Levenberg-Marquardt” algorithm (8) is implemented using the MATLAB function lsqnonlin with (7) computed from the results of the COMSOL simulations.
Results and Discussion
In this section we apply the ICS for the detection and concentration estimation of streptavidin and ferritin using a biotin receptor. The numerically estimated conductance for both the streptavidin and ferritin computed using (3a) and (6) with boundary conditions (5) and parameters estimated from (8) are in excellent agreement with the experimentally measured conductance. Note that the conductance is estimated using (2) with the drive potential having a magnitude of 20 mV.
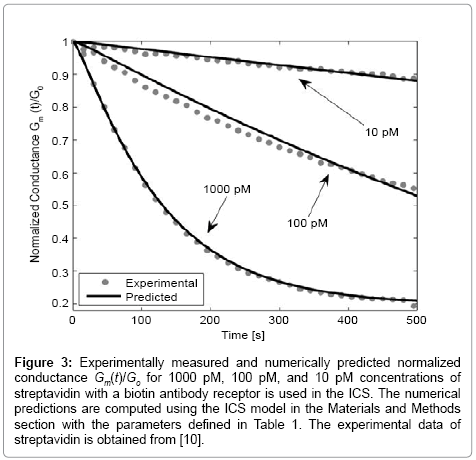
Figure 3 presents the numerically estimated and measured conductance of the ICS for the detection of streptavidin for known concentrations of 1000 pM, 100 pM, and 10 pM. As seen in Figure 3, the experimentally measured and numerically predicted conductance are in excellent agreement. Note that for low analyte concentrations, the diffusive properties of the analyte greatly influence the population of gA dimers on the surface of the ICS. As seen from Figure 3, using the advection-diffusion PDE coupled with the surface reaction allows an accurate estimate of analyte concentrations of pM concentration. By adjusting the number of binding cites and flow rate, it is possible to use the ICS to detect femto-molar concentrations of species [11,12]. The selection of the number of binding cites and flow rate optimal for detecting a certain concentration of analyte species can be done using (3a) and (6) with boundary conditions (5).
Figure 3: Experimentally measured and numerically predicted normalized conductance Gm(t)/Go for 1000 pM, 100 pM, and 10 pM concentrations of streptavidin with a biotin antibody receptor is used in the ICS. The numerical predictions are computed using the ICS model in the Materials and Methods section with the parameters defined in Table 1. The experimental data of streptavidin is obtained from [10].
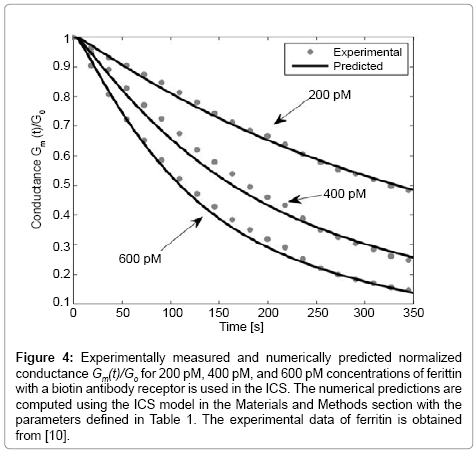
To illustrate the detection capability of the ICS for large analyte molecules, we consider the detection of ferritin which has a molecular weight of 450 kDa, as compared with streptavidin with a molecular weight of 52.8 kDa. Note that for the detection of ferritin, biotinylated antibody receptors are added to the solution that bind to the ferritin molecules. The ferritin biotinylated antibody complexes then bind to the tethered membrane biotinylated lipid molecules. Figure 4 presents the numerically estimated and measured conductance of the ICS for the detection of ferritin for known concentrations of 200 pM, 400 pM, and 600 pM. As seen in Figure 3, the experimentally measured and numerically predicted conductance are in excellent agreement.
Figure 4: Experimentally measured and numerically predicted normalized conductance Gm(t)/Go for 200 pM, 400 pM, and 600 pM concentrations of ferittin with a biotin antibody receptor is used in the ICS. The numerical predictions are computed using the ICS model in the Materials and Methods section with the parameters defined in Table 1. The experimental data of ferritin is obtained from [10].
What is the lower limit of analyte concentration that could be measured using the ICS? Since the detection mechanism of the ICS is dependent on detecting changes in membrane conductance, the question is equivalent to asking when is 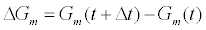 detectable. The tethered archaebacterial membrane in the ICS with no embedded ion channels has a conductance of 1 μS with a standard deviation of σ=0.05 μS as estimated from experimental measurements. To ensure the measured change in membrane conductance is a result of the population change of conducting gA dimers and not random thermal fluctuations of the membrane, a ΔGm>3σ is required. The conduction of a gA dimer is in the range of 0.8-2.0 pS [22,23]. Therefore a minimum of 75,000 gA dimers must close for the conductance change to be detectable. This corresponds to a surface concentration of approximately 60 attomolar. Taking into account diffusion effects, binding kinetics, and thermal noise, we safely assume that the ICS can be designed to detect femtomolar concentrations of target species.
detectable. The tethered archaebacterial membrane in the ICS with no embedded ion channels has a conductance of 1 μS with a standard deviation of σ=0.05 μS as estimated from experimental measurements. To ensure the measured change in membrane conductance is a result of the population change of conducting gA dimers and not random thermal fluctuations of the membrane, a ΔGm>3σ is required. The conduction of a gA dimer is in the range of 0.8-2.0 pS [22,23]. Therefore a minimum of 75,000 gA dimers must close for the conductance change to be detectable. This corresponds to a surface concentration of approximately 60 attomolar. Taking into account diffusion effects, binding kinetics, and thermal noise, we safely assume that the ICS can be designed to detect femtomolar concentrations of target species.
Conclusion
In this paper we have presented the formation, dynamic models, and experimental measurements using the ICS biosensor. Key features include using a lumped circuit model for the bioelectronic interface, electrolyte, and tethered membrane allowing the conductance of the membrane to be estimated from current measurements. The membrane conductance is related to the population of conducting gramicidin dimers. The population of conducting dimers is dependent on the electrodiffusive behaviour of the target molecule of interest and the chemical reactions at the tethered membrane surface. Employing an advection-diffusion partial differential equation coupled with nonlinear interface boundary conditions, we illustrated how the concentration of specific analyte molecules can be computed using a maximum-likelihood estimator which simultaneously estimated the surface reaction rates of the ICS. Given the dynamic models presented in this work coupled with engineered receptors allows the ICS to be used for a host of applications for rapid detection of specific analyte molecules in cluttered electrolyte environments.
References
- Kyu Kim S, Cho H, Park HJ, Kwon D, Min Lee J, et al. (2009) Nanogap biosensors for electrical and label-free detection of biomolecular interactions. Nanotechnology 20: 455502.
- Mathwig K, Lemay S (2013) Mass transport in electrochemical nanogap sensors. Electrochimica Acta 112: 943-949.
- Esfandyarpour R, Javanmard M, Koochak Z, Esfandyarpour H, Harris J, et al. (2013) Label-free electronic probing of nucleic acids and proteins at the nanoscale using the nanoneedle biosensor. Biomicrofluidics 7: 044114.
- Cranfield CG, Cornell BA, Grage SL, Duckworth P, Carne S, et al. (2014) Transient potential gradients and impedance measures of tethered bilayer lipid membranes: pore-forming peptide insertion and the effect of electroporation. Biophys J 106: 182-189.
- Heinrich F, Ng T, Vanderah DJ, Shekhar P, Mihailescu M, et al. (2009) A new lipid anchor for sparsely tethered bilayer lipid membranes. Langmuir 25: 4219-4229.
- McGillivray DJ, Valincius G, Vanderah DJ, Febo-Ayala W, Woodward JT, et al. (2007) Molecular-scale structural and functional characterization of sparsely tethered bilayer lipid membranes. Biointerphases 2: 21-33.
- Cornell BA, Braach-Maksvytis VL, King LG, Osman PD, Raguse B, et al. (1997) A biosensor that uses ion-channel switches. Nature 387: 580-583.
- Raguse B, Braach-Maksvytis V, Cornell B, King L, Osman P, et al. (1998) Tethered lipid bilayer membranes: Formation and ionic reservoir characterization. Langmuir 14: 648-659.
- Prashar J, Sharp P, Scarffe M, Cornell B (2007) Making lipid membranes even tougher. Journal of Materials Research 22: 2189-2194.
- Moradi-Monfared S, Krishnamurthy V, Cornell B (2012) A molecular machine biosensor: Construction, predictive models and experimental studies. Biosens Bioelectron 34: 261-266.
- Krishnamurthy V, Monfared S, Cornell B (2010) Ion-channel biosensors Part I: Construction, operation, and clinical studies. IEEE Transactions on Nanotechnology 9: 303-312.
- Krishnamurthy V, Monfared SM, Cornell B (2010) Ion channel biosensors Part II: Dynamic modeling, analysis, and statistical signal processing. IEEE Transactions on Nanotechnology 9: 313-321.
- Lomize AL, Orekhov VIu, Arsen'ev AS (1992) [Refinement of the spatial structure of the gramicidin A ion channel]. Bioorg Khim 18: 182-200.
- Hendrickson WA, Pähler A, Smith JL, Satow Y, Merritt EA, et al. (1989) Crystal structure of core streptavidin determined from multiwavelength anomalous diffraction of synchrotron radiation. Proc Natl Acad Sci U S A 86: 2190-2194.
- Theil EC (1987) Ferritin: structure, gene regulation, and cellular function in animals, plants, and microorganisms. Annu Rev Biochem 56: 289-315.
- DeChancie J, Houk KN (2007) The origins of femtomolar protein-ligand binding: hydrogen-bond cooperativity and desolvation energetics in the biotin-(strept) avidin binding site. J Am Chem Soc 129: 5419-5429.
- Myszka DG, He X, Dembo M, Morton TA, Goldstein B (1998) Extending the range of rate constants available from BIACORE: Interpreting mass transport-influenced binding data. Biophys J 75 583-594.
- Qian S, Bau HH (2003) A mathematical model of lateral flow bioreactions applied to sandwich assays. Anal Biochem 322: 89-98.
- Chung SH, Andersen OS, Krishnamurthy V (2007) Biological membrane ion channels. Biological And Medical Physics Biomedical Engineering.
- Oh SY, Cornell B, Smith D, Higgins G, Burrell CJ, et al. (2008) Rapid detection of influenza A virus in clinical samples using an ion channel switch biosensor. Biosens Bioelectron 23: 1161-1165.
- Woodhouse G, King L, Wieczorek L, Osman P, Cornell B (1999) The ion channel switch biosensor. J Mol Recognit 12: 328-334.
- Allen TW, Andersen OS, Roux B (2004) Energetics of ion conduction through the gramicidin channel. Proc Natl Acad Sci U S A 101: 117-122.
- Rudnev VS, Ermishkin LN, Fonina LA, Rovin YuG (1981) The dependence of the conductance and lifetime of gramicidin channels on the thickness and tension of lipid bilayers. Biochim Biophys Acta 642: 196-202.
- Krishna G, Schulte J, Cornell BA, Pace R, Wieczorek L, et al. (2001) Tethered bilayer membranes containing ionic reservoirs: the interfacial capacitance. Langmuir 17: 4858-4866.
- Krishna G, Schulte J, Cornell BA, Pace RJ, Osman P (2003) Tethered bilayer membranes containing ionoic reservoirs: selectivity and conductance. Langmuir 19: 2294-2305.
- Yin P, Burns CJ, Osman PD, Cornell BA (2003) A tethered bilayer sensor containing alamethicin channels and its detection of amiloride based inhibitors. Biosens Bioelectron 18: 389-397.
- Zaccari I, Catchpole BG, Laurenson SX, Davies AG, Wälti C (2014) Improving the dielectric properties of ethylene-glycol alkanethiol self-assembled monolayers. Langmuir 30: 1321-1326.
- Lenzi EK, de Paula JL, Silva FRGB, Evangelista LR (2013) A connection between anomalous Poisson-Nernst-Planck models and equivalent circuits with constant-phase elements.
- Quintana JJ, Ramos A, Nuez I (2013) Modeling of an EDLC with fractional transfer functions using Mittag-Leffler equations. Mathematical Problems in Engineering 2013.
- Højgaard Olesen L, Bazant MZ, Bruus H (2010) Strongly nonlinear dynamics of electrolytes in large ac voltages. Phys Rev E Stat Nonlin Soft Matter Phys 82: 011501.
- López-García JJ, Horno J, Grosse C (2012) Equilibrium properties of charged spherical colloidal particles suspended in aqueous finite ion size and effective ion permittivity effects. J Colloid Interface Sci 380: 213-221.
- Kilic M, Bazant M, Ajdari A (2007) Steric effects in the dynamics of electrolytes at large applied voltages. II. modified Poisson-Nernst-Planck equations. Phys Rev E 75: 021503.
- Wang H, Thiele A, Pilon L (2013) Simulations of cyclic voltammetry for electric double layers in asymmetric electrolytes: a generalized modified Poisson-Nernst-Planck model. J Phys Chem C 117: 18286-18297.
Relevant Topics
Recommended Journals
Article Tools
Article Usage
- Total views: 15578
- [From(publication date):
specialissue-2015 - Aug 19, 2025] - Breakdown by view type
- HTML page views : 10900
- PDF downloads : 4678