Research Article Open Access
Non-Radiometric Dating of the Age of the Earth: Implications From Fossil Coral Evidence
Nurbek Mazhenov and Sanzhar Shalkarbekov*Institute of Information and Computing Technologies, Committee of Science, Ministry of Education and Science, Almaty, Kazakhstan
- *Corresponding Author:
- Sanzhar Shalkarbekov
Researcher, Institute of Information and Computing Technologies
Committee of Science, Ministry of Education and Science
Almaty, Kazakhstan
Tel: +7(777)2247160
E-mail: shalkars@gmail.com
Received date: July 21, 2015; Accepted date: August 07, 2015; Published date: August 17, 2015
Citation: Mazhenov N, Shalkarbekov S (2015) Non-Radiometric Dating of the Age of the Earth: Implications From Fossil Coral Evidence. Int J Adv Innovat Thoughts Ideas 3:160. doi: 10.4172/2277-1891.1000160
Copyright: © 2015 Mazhenov N. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at International Journal of Advance Innovations, Thoughts & Ideas
Abstract
Radioisotope dating has revealed that the age of the Earth is 4.54–4.6 billion years, and these results are widely accepted. However, as with all searches for truth in science, facts should be supported by multiple lines of evidence. Thus, determining the age of the Earth with alternative techniques could serve to strengthen the conclusions that have been reached with radioisotope dating methods. In this paper, a different approach to solving the problem is proposed. As is known from studies of 400 million year old fossil corals, Earth years were 400 days in duration in distant times because the Earth rotated faster than it does today. According to calculations based on the fundamental law of rotational motion dynamics involving the moment of inertia of a body, the radius of the ancient Earth 400 million years ago was 553.379 km less than it is today. This brings us to the impressive conclusion that Earth’s radius grew on average by 1.3834475 mm per year over the past 400 million years. Let us call this the evolutionary Earth growth constant; it does not take into account the effect of lunar tidal friction. If the present day Earth radius of 6371 km is divided by 1.3834475 mm per year, we can estimate the growth time of the Earth from its beginning to the presentthe growth time is 4.6 billion years, which is consistent with the radioisotope data, i.e., 4.6 billion years equals the age of the Earth! This new method for measuring Earth’s age not only confirms outcomes obtained with radiological methods, but it poses new problems and avenues of research for paleogeologists.
Keywords
Age of the Earth; Earth’s radius; Radioisotope dating; Non-radioisotope dating; Fossil corals
Introduction
Earth’s history from the moment of its birth has been an important subject of geological science. One of the key goals has been to not only determine the conditions surrounding the formation of Earth, but also the whole evolutionary sequence of Earth and periodization of all major geological events. Our attention here is focused on the characterization of geological time that encompasses the evolutionary sequence of the material geological environment, or more accurately, the stratigraphic divisions. We call time geological due to specifics regarding the fixation of geological events over billions of years. Stratigraphic divisions are associated with certain development stages, and then they disappear as they are replaced by other divisions i.e., basically they represent time categories that form the geological history. Exhaustive knowledge on methodological aspects of geological theories and isotope time sequences has been demonstrated in many works, for example, the work by Wells [1].
Studies of geological time typically begin with event relation determinations (early–late events, ancient–recent events) and finish with continuity determinations and positioning on the modern geochronological scale. These studies may involve both qualitative and quantitative observations.
Qualitative (topological) treatments of geological time are ultimately connected to quantitative (metric) treatments. Specifically, topological characteristics are often used for determining the relative age and order of discreet geological events, whereas metric characteristics are used to determine the specific ages and lengths of geological events. In the latter case, quantitative estimates of time are conducted in modern astronomical units—years or Earth’s rotation time around the Sun.
Specific geological ages, which can be referred to as absolute times versus relative times, are determined conventionally by radiometric methods. Such estimates can span from the modern era into the deep geological past and are presented in descending order (i.e., from the past to the present). The estimates are derived from isotope data, which are converted into radiological ages.
Relative geological times for events in Earth’s history are presented in relation to times of other geological events. These times are determined based on corresponding positions of ground layers, i.e., lower layers are ancient in unbroken ground layers, whereas the upper ones are younger. Organic fossil remains contained in older geological layers provide important insight into the stratigraphic scale.
What relation exists between absolute and relative geological times? For example, are the data complementary or incongruent? The goal of this work is to find the answer to this question. To begin, let us refer to following facts, whose truths remain undisputable among many researchers: the age of the Earth is 4.6 billion years, the average radius of the Earth is 6371 km, the Earth revolves around the Sun over a period of one year, each year contains 365 days, and each day has 24 hours. However, some of these numbers are not constants. Growth data from 400 million year old fossil corals indicate that Earth years were 400 days in duration in distant times, i.e., the Earth rotated faster in the past [2,3]. According to calculations based on the fundamental law of rotational motion dynamics involving the moment of inertia of a body, the radius of the ancient Earth 400 million years ago was 553.379 km less than it is today. From such calculations, it can be assumed that Earth’s radius over the past 400 million years has increased on average by 1.3834475 mm per year (e.g., 553.379 km/400,000,000 years=1.3834475 mm per year). This is an unusual conclusion that is difficult to accept using common sense. However, if we follow through with this logic and extend the growth rate over Earth’s entire geological history, then present day Earth with a radius of 6371 km could have been formed in 4.6 billion years. Let us check: 6371 km/1.383 mm per year=4.6 billion years—this is the age of the Earth!
Let us name the value of 1.3834475 mm per year as the evolutionary Earth growth constant; the following discussion does not take into account the effect of lunar tidal friction. The formula for estimating Earth’s absolute age is as follows:
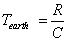
Where R is the average Earth radius and С is the evolutionary Earth growth constant of 1.383 mm per year.
The abovementioned results complement, and thus strengthen the truth of, estimates of the absolute age of the Earth that were determined by radiometric methods. Along with this conclusion, the evolutionary Earth growth constant of 1.383 mm per year found by us allows for new insights into Earth’s origin and evolution.
According to the Kant-Laplace hypothesis, Earth was formed via accretionary processes involving gases and dust masses that remained after the formation of the Sun. These processes were largely completed over a time span of 10–20 million years. We do not share this point of view given that our research suggests that Earth has been growing gradually by 1.383 mm per year.
The Earth growth hypothesis suggested here is not new; it was first suggested at the beginning of the twentieth century. Since that time, this hypothesis has been actively developing and has modern supporters. However, much of this research was treated as obsolete after the development of plate tectonics theory. The evolutionary Earth growth constant found by us can serve as solid ground to revive the expanding Earth hypothesis.
Methods and Results
Kant-Laplace hypothesis
The greatest thinkers of our planet have been fascinated by questions about the origin and evolution of the planetary system and the Sun. Philosopher Kant and mathematician Laplace along with many astronomers and physicists of the nineteenth and twentieth centuries tackled this problem. Although much understanding has been gained over the past two centuries, conclusive answers to questions pertaining to the origin and evolution of our solar system are still not clear.
In the classical Kant-Laplace hypothesis, angular momentum is the most important characteristic of an isolated mechanical system, which our Sun and its surrounding planets are. The whole process of planetary evolution, from the initial stage of cosmic nebula to the formation of the Sun and the eight planets, was in strict accordance with angular momentum.
The rotation consists of the orbital motion of the planets and the axial rotation of the Sun and the planets. Angular momentum of each planet relative to the center of mass (almost coinciding with the center of the Sun) is defined as the product of the mass of the planet, its speed, and the distance to the center of rotation, e.g., for the Sun: 2/5 M · v · R, where M is the mass of the body, R is the radius, and v is the equatorial velocity. Although the mass of all the planets combined is only 1/700 of that of the Sun, 98% of the solar system’s momentum is attributed to the orbital motion of the planets, while only 2% is attributed to the Sun’s rotation around its axis. Angular momentum associated with the rotation of the planets around their axes is negligible because of the relatively small masses of the planets and their radii [4].
Approaches for calculating the age of the Earth
How old is the Earth? This is one of the most important concerns for humanity, as the Earth is the cradle of humankind and all living beings. The answer can be found in many scientific reference materials. However, the history of the establishment of Earth’s age as scientific fact is incredible. Presently, Christian, Islamic, and Judaic scholars insist that the age of the Earth and the universe is not more than 6000 to 12,000 years, and their views are based on religious texts. Importantly, these sacred texts are based on symbolic years and periods. Yet, it is worthwhile to note that even the history of the development of scientific methods for determining the age of the Earth is full of blind alleys and misconceptions.
Lord Kelvin (W. Thomson) published a series of works between 1862 and 1899 devoted to the determination of the age of the Earth. He assumed that the Earth formed in a liquid state, and then, it began to cool as heat radiated from its surface. Using the theory of heat conduction, he calculated the time required for the Earth to cool to its modern temperature. Thomson, in his famous article titled “The Age of the Earth as an Abode Fitted for Life,” posited that our planet is between 20 to 400 million years old. This hypothesis brought Thomson into dispute with the great naturalist Charles Darwin, who knew that the discovery of radioactivity by Becquerel in 1897 would resolve this dispute in the future. American chemist Willard Libby developed the absolute radiocarbon dating method for organic subjects in 1946, and he won the Nobel Prize for chemistry in 1960 for his work. Quickly, researchers realized that radioactive elements could work as natural clocks, as radioactive decay adheres to strict time patterns.
The majority of evolutionists accept the current estimated age for the Earth and our solar system of 4.54 ± 0.02 billion years. What is this based on? This estimate was derived from the ratios of various lead isotopes found in meteorites. Using this method, the oldest terrestrial rocks have been characterized as being 3.96 billion years old (Slave Province, Canada) and the oldest meteorite has been estimated at 4.6 billion years old [5,6].
Presently, scientists tend not to argue over the age of the Earth, largely as a result of the continued development of the radiometric dating method and elimination of some of its shortcomings. However, additional evidence is required in order to determine the age of the Earth accurately. This is because the radiometric method, which indicates an Earth age of 4.54 billion years, takes into account the duration of decay of atoms of some elements (uranium, radium, thorium, etc.) but not the Earth as a whole. In other words, it would be beneficial to determine the age of the Earth on a different basis.
Fossil coral effect
In this paper, a different approach to solving the problem is proposed. As is known from studies of 400 million year old fossil corals, Earth years were 400 days in duration during distant times. This fact was detected through analyses of the growth lines on the bodies of fossil corals, whereby every specific line represents a year, similar to the rings on a cut tree [7,8].
In the past, the Earth rotated faster than it does today. We shall now turn to the physics of solid body rotation to study this phenomenon. Let us consider the main categories of rotational movements and discuss the fundamental law of rotational motion dynamics.
The moment of inertia of a body defines the inertia of that body with respect to rotational motion. The moment of inertia includes the impact of the angular acceleration of a body mass, its geometrical dimensions, location of the mass relative to the axis of rotation, and distribution of the mass in the volume of the body. Mass moment of inertia m located at a distance r from the axis is taken to be equal to
J = m. r2 (2)
The kinetic energy of a rotating body is equal to half the product of its moment of inertia and the square of the angular velocity as follows:
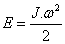
We will denote the kinetic rotation energy of the small trial mass (coral size) when accounting for Earth’s daily rotation at its surface 400 million years ago and today as E1 and E2 respectively. In accordance with the law of kinetic energy conservation, we can state that E1 and E2, which means that
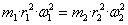 (4)
(4)
Where 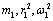 are the mass, radius, and angular velocity of the
Earth 400 million years ago and
are the mass, radius, and angular velocity of the
Earth 400 million years ago and 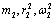 are the mass, radius, and
angular velocity of the Earth today.
are the mass, radius, and
angular velocity of the Earth today.
Assuming that mass m1 m1 is equal to or negligibly different from
m2, i.e., 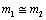 will allow us to cancel out the masses and simplify
equation (4). Thus, from equation (4) after canceling out masses
m1 and m2 , we can obtain an analytical value for the radius of the Earth
400 million years ago as follows:
will allow us to cancel out the masses and simplify
equation (4). Thus, from equation (4) after canceling out masses
m1 and m2 , we can obtain an analytical value for the radius of the Earth
400 million years ago as follows:
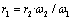 (5)
(5)
Where ω1 = 2π / T1 is the angular velocity of the Earth 400 million years ago and ω2 = 2π / T2 is the angular velocity of the Earth today.
Using the number of days in the year derived from ancient corals, we can determine the length of a day and the number of seconds in an Earth year 400 million years ago. For the calculations, we shall use the sidereal day on Earth, which in the year 2000 was 23 h, 56 min, and 4.090530833 s, thus consisting of a total of 86,164.090530833 s; accordingly, the number of seconds for an ancient Earth year is equal to 365.2564 d (86,164.090530833 s/400 d)=78,679.96379141538 s, which is equivalent to 21.86 h.
Let us now calculate the ancient Earth’s radius using formula (4), where T1=78,679.964 s, T2=86,164.091 s and the average radius of the Earth r2 = 6371 km:
r1=6371km 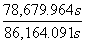 =5817.621km
=5817.621km
As expected, the Earth’s radius has increased over 400 million years by Δ=6371 km -5817.621 km=553.379 km. Therefore, Earth’s radius has increased on average by 1.3834475 mm per year over the past 400 million years, i.e., 553.379 km/400,000,000 years=1.3834475 mm per year.
Let us call 1.3834475 mm per year the evolutionary Earth growth constant; this does not take into account the effect of lunar tidal friction. This constant will allow us to estimate the growth of the Earth from its beginning to the present, whereby 6,371,000,000 mm/1.3834475 mm per year=4.6 billion years, which is consistent with the reference data, and 4.6 billion years equals the age of the Earth!
Lunar factors involved in the slowing of the Earth’s rotation
Is there a more precise way to calculate the age of the Earth? Yes, there is, if we consider the effect of the Moon, the Earth’s satellite. Doubts regarding the constancy of the Earth’s rotation speed arose after the discovery of the secular acceleration of the Moon’s motion by Halley in 1695. Kant first proposed the idea of the secular slowing rotation of the Earth under the influence of tidal friction in 1755. In the second half of the last century, irregular fluctuations in the Earth’s rotation and movement of the geographical poles were discovered. Since then, the uneven rotation of the Earth and the motion of the poles have been monitored on a regular basis.
Based on the analysis of hundreds of solar and lunar eclipses over the last 2700 years, Richard Stephenson from Durham University in the UK concluded that the terrestrial day is getting longer by almost 0.000002 seconds per year [9,10]. According to from the Hydrometeorological Center of Russia in Moscow, the tidal projections on the Earth’s surface are constantly following the Moon and the Sun from east to west, i.e., in the direction opposite to the daily rotation of the Earth. Naturally, such movement in the oceans and on the Earth causes frictional forces that slow the rotation of the planet. This results in the secular slowing of the Earth’s rotation. It is estimated that because of this phenomenon, the duration of the day has lengthened by 0.00003 seconds [10].
Let us now calculate the age of the Earth based on Richard Stephenson’s value for moon braking of 0.000002 seconds. Over 400 million years, the Earth’s rotation will have slowed as follows: 400,000,000 0.000002 s=800 s.
1. Let us calculate the radius of the Earth 400 million years ago by taking into account Stephenson’s moon braking value of 800 s:
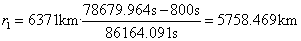 (7)
(7)
2. Then, the evolutionary Earth growth constant by taking into account the moon braking value of 800 s is as follows: (6371 km - 5758.469 km)/400,000,000 years=1.5313275 mm/year.
3. Lastly, the calculation for the age of the Earth based on Stephenson’s moon braking value of 800 s is as follows: (6371 km/1.5313275 mm/year=4.16 billion years.
Correspondingly, we can calculate the age of the Earth based on Siderenkov’s moon braking value of 0.00003 s. In this case, the Earth’s slowing rotation due to the Moon over 400 million years will be 400,000,000 0.00003 s=12,000 s, and the calculated age for the Earth is 1.77 billion years. Such a wide range for the calculated effects of the Moon’s impact on the Earth’s rotation indicates the incompleteness of this solution and requires further clarifications to reduce the uncertainties.
We propose an empirically calculated time for the slowing rotation of the Earth due to the effect of the Moon, which is 0.00000025 seconds and corresponds to the Earth’s age of 4.54 billion years. The age of the Earth as determined through the use of radiological methods will be a measure of the reliability of our calculations.
For clarity, the above calculations are summarized in Table 1. From Table 1, we can see that the Moon’s effect on the duration of an Earth day-lines 3 and 4- does not significantly affect the final results, which coincide with the age of the Earth calculated using radiological methods.
| Item No. | Moon’s effect on the duration of the Earth day(seconds) | Radius of the Earth400 million years ago(km) | Evolutionary Earth growth constant(mm/year) | Age of the Earth (billion years) |
|---|---|---|---|---|
| 1 | 0.00003 | 4930.337 | 3.6016561 | 1.77 |
| 2 | 0.000002 | 5758.469 | 1.5313273 | 4.16 |
| 3 | 0.00000025 | 5810.227 | 1.4019318 | 4.54 |
| 4 | 0.0 | 5817.621 | 1.3834475 | 4.6 |
Table 1: Calculations for the age of the Earth.
Discussion and Conclusion
Can we state that the dating method described herein is purely nonradiological? If we take into account equation (1), and the following variables are used, namely, R for the average Earth radius and C for the evolutionary Earth growth constant, C amounts to 1.383 mm per year. From this standpoint, the age of Earth calculation method can be considered as non-radiological. The main issue here is that to calculate C, ancient corals were used whose absolute age of 400 million years was determined by radiological methods. However, this concern becomes insubstantial considering that coral annual rings and fundamental physics laws were used.
Now we turn to the idea of the growth of the Earth itself. Originating in the early twentieth century, the expanding Earth hypothesis has since been actively developed and has gained a number of supporters. However, much of the relevant research was considered obsolete after the development of plate tectonics theory in the 1960–1970s.
Currently, a number of research papers support the following common view. “According to current measurements in DORIS, GPS, GRACE, VLBI projects, the radius of the Earth in the XXI century has not been changing (the measurement error does not exceed 0.2 mm per year) [11-13]. The paleomagnetic and paleogeologic data suggest that the radius of the Earth has not changed significantly over the last 400–600 million years at least” [14,15].
Xiaoping Wu from NASA’s (National Aeronautics and Space Administration) scientific research team concluded that the Earth is not expanding. Specifically, he and an international group of scientists used new methodology for calculating the data and concluded that the average change in the Earth’s radius is 0.004 inches (0.1 mm) per year, or about the thickness of a human hair, which is considered statistically insignificant [13].
The measurement accuracy of the NASA researchers data was high and of good quality. However, the experiment covered a period of time that is negligible in comparison to the age of the Earth. Therefore, it is possible that the growth of the Earth stabilized during the course of the experiment and it is too early to state that the theory of the growing Earth is false.
In fact, paleontological evidence suggests the opposite. According to Samuel Warren Carey, professor of geology at the University of Tasmania in Australia, the Earth was twice as small in diameter 200 million years ago as it is now (please note that according to our estimates, the radius of the Earth was 280.4 km less than its current measurement). Some people were carried away with the revolutionary novelty of his scientific credo-the presentation and justification of the concept of the expansion of the Earth-while others were spurred to further thinking on the subject; still others fiercely defend traditional views [16]. Professor Derek Ager, in the introduction to his presidential address in 1986 to the geology section of the British Association for Advancement of Science, wrote: “As a paleontologist naturally I prefer the evidence provided by fossils, especially the Mesozoic brachiopods, which I have studied for some 35 years.” At the end of the address, he concluded: “I find it difficult to accept different explanations for the same phenomena which occurred in the various great oceans of the world. On balance, I prefer to think that all the oceans have been expanding since early Mesozoic times and that therefore the hypothesis of an expanding Earth is inescapable” [16].
Justification of Calculations (Study Logic)
The 1930s witnessed an intense scientific debate about the effects on the Earth from gravitational tidal interactions of the Earth and Moon and the increased moment of inertia. Warren Carey devoted Chapter 14, titled “Criticism of Earth Expansion,” of his monograph to these issues and outlined evidence in the following sections: Surface Gravity; The Volume of Seawater; Paleomagnetism; Growth Lines of Fossil Corals; The Blinkers of Dogma; and Other Planets [16]. Some of the objections to the concept of Earth expansion were raised on the following grounds: “If the Earth were originally half of its present diameter, gravity acceleration at the surface would be so high that it would show up inevitably in ancient geological processes. The total volume of seawater would submerge all lands to a depth of 2 km or more. Paleomagnetic data show that Earth’s radius has not changed since the end of the Paleozoic. Growth lines on fossil corals indicate that the number of days in the year 400 million years ago and at intervening times are consistent with tidal retardation of the Earth, whereas change in the moment of inertia of the Earth implied by expansion is inconsistent” [16].
The main argument against an increase in the radius of the Earthchanges in the moment of inertia of the Earth-was the orthodox assumption that the effect of the Moon is the main cause of the slowing of Earth’s rotation. However, this approach to solving the problem is contrary to the physical laws of the conservation of energy, momentum, and angular momentum. Rather than assuming that increased moment of inertia and the Moon’s tidal friction were mutually exclusive effects on the slowing rotation of the Earth during the 400 million year period, we can assume that both had an effect.
Our task is thus reduced to the estimation of the relative contributions of the two factors involved in the Earth’s rotational slowing (Table 1), line 4 reflects the effect of the moment of inertia without the Moon’s tidal friction, and these values give an estimated age of the Earth of 4.6 billion years. Table 1, line 3 shows the numerical values corresponding to calculations that consider the contributions of both of the two factors, and these values give an estimated age of the Earth of 4.54 billion years. This coincides with the results obtained by radiological methods. In this case, 400 million years ago, Earth’s radius was 5810.23 km or 560.77 km less than at present. The evolutionary Earth growth constant was 1.4019318 mm per year. The magnitude of the moon braking effect on the Earth’s rotation is 0.00000025 seconds per day.
So, on one metaphorical side of the scale, we place one factor, the law of conservation of moment of inertia, and on the other, we place lunar tidal friction. In what ratio shall we split the retardation of the Earth’s rotation over 400 million years between these two factors? The decision criterion can be a time scale that coincides with the radiometric dated age of the Earth.
By assuming that the Earth and planets grow over time, we can logically ask the following basic questions: how does the Earth grow and what is the source of its growth? A single answer does not exist. There are a number of hypotheses; one of them is that the stars and planets arise from the surrounding space—the space vacuum. This follows from one of the theses put forth during the recent revolution in cosmology, namely, that the universe is dominated by a vacuum with an energy density greater than the density of all other forms of cosmic energy combined [17]. This theory has arisen from reliable observational data obtained by astronomers who have been studying distant supernovae [18].
What relationship exists between the world of the space vacuum and the solar system? This relationship, from the perspective of fundamental physics, has not been established in a straightforward and evident manner. This is an immense topic, the discussion of which is beyond the scope of this article.
Acknowledgements
We are thankful to our friends and colleagues for valuable discussions and comments that were necessary to consider during the course of this work. We would particularly like to thank Pavel Ozernov, Shamshi Aipanov, Anatoly Matafonov, and Kubaidulla Makhutov for their insights.
References
- Wells JW(1963)Coral growth and geochronometry. Nature 197: 948-950.
- Kuzmicheva EI (1982) Corals as “geological clocks.” Priroda 10: 19-25.
- Shklovsky JS (1987) Universe, Life, Mind (Russian original).Nauka Moscow.
- Dalrymple GB(1991a)So How Old Is the Earth, Anyway. NCSE Reports11: 1- 17.
- Dalrymple GB (1991b)The Age of the Earth. Stanford University Press, Stanford.
- Dubnischeva T(1997) Concepts of Modern Science.In: Zhukov MF (ed.) YUKEA LLC, Novosibirsk.
- Schmidt PW, Clark DA(1980)The response of palaeomagnetic data to Earth expansion. Geophysical Journal of the Royal Astronomical Society 61: 95-100.
- Stephenson FR(2008)How reliable are archaic records of large solar eclipses? Journal for the History of Astronomy 39: 229 -250.
- Sidorenkov N (2003) Instability of the Earth’s Rotation.Hydrometeorological Center of Russia, Moscow.
- NASA (2011) NASA Research Confirms it’s a Small World, After All. Jet Propulsion Laboratory, National Aeronautics and Space Administration, Pasadena, California.
- ScienceDaily(2011)It’sa Small World, After All: Earth Is Not Expanding, NASA Research Confirms, ScienceDaily.
- Wu X, Collilieux X, Altamimi Z, Vermeersen BLA, Gross RS,et al.(2011) Accuracy of the International Terrestrial Reference Frame origin and Earth expansion. Geophysical Research Letters 38: L103304.
- McElhinney MW, Taylor SR, Stevenson DJ(1978) Limits to the expansion of Earth, Moon, Mars, and Mercury and to changes in the gravitational constant. Nature 271: 316-321.
- Williams GE(2000) Geological constraints on the Precambrian history of the Earth’s rotation and the moon’s orbit. Reviews of Geophysics 38: 37-59.
- Carey SW(1991) Theories of the Earth and the Universe. Mir, Moscow (Russian translation from English).
- Chernin AD(2001) Cosmic vacuum. UspekhiFizicheskikhNauk 171: 1153-1175.
- Riess AG, Filippenko AV, Challis P, Clocchiatti A, Diercks A (1998) Observational evidence from supernovae for an accelerating universe and a cosmological constant. The Astronomical Journal 116: 1009-1038.
- Perlmutter S, Aldering G, Goldhaber G, Knop RA, Nugent P (1999)The Supernova Cosmology ProjectMeasurements of Ω and Λ from 42 high-redshift supernovae. The Astrophysical Journal 517: 565-586.
Relevant Topics
- Advance Techniques in cancer treatments
- Advanced Techniques in Rehabilitation
- Artificial Intelligence
- Blockchain Technology
- Diabetes care
- Digital Transformation
- Innovations & Tends in Pharma
- Innovations in Diagnosis & Treatment
- Innovations in Immunology
- Innovations in Neuroscience
- Innovations in ophthalmology
- Life Science and Brain research
- Machine Learning
- New inventions & Patents
- Quantum Computing
Recommended Journals
Article Tools
Article Usage
- Total views: 19716
- [From(publication date):
September-2015 - Aug 30, 2025] - Breakdown by view type
- HTML page views : 15044
- PDF downloads : 4672
