Conference Proceeding Open Access
Optimization of Medium Components for the Production of Phytase by R. Oryzae using Statistical Approaches
| Richa Rani1*, Sidharth Arora1, Sudhir Kumar2 and Sanjoy Ghosh1 | |
| 1Department of Biotechnology, Indian Institute of Technology, India | |
| 2Department of Biochemistry, All India Institute of Medical Sciences, India | |
| Corresponding Author : | Richa Rani Department of Biotechnology Indian Institute of Technology Roorkee, India Tel: +91–1332–285424 Fax: +91–1332–273560 E-mail: richa3biotech@yahoo.co.in |
| Received July 31, 2013; Accepted November 18, 2013; Published November 25, 2013 | |
| Citation: Rani R, Arora S, Kumar S, Ghosh S (2013) Optimization of Medium Components for the Production of Phytase by R. Oryzae using Statistical Approaches. J Bioremed Biodeg S18:003. doi:10.4172/2155-6199.S18-003 | |
| Copyright: © 2013 Rani R, et al. This is an open-a ccess article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. | |
Related article at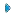 Pubmed Pubmed 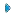 Scholar Google Scholar Google |
|
Visit for more related articles at Journal of Bioremediation & Biodegradation
Abstract
The aim of this study was to determine the optimum levels of nutrients for the production of phytase by heat stressed Rhizopus oryzae in submerged fermentation. Plackett-Burman Design (PBD) was initially adopted for evaluating the medium components (mannitol, K2HPO4, Na2HPO4 and sodium phytate) affecting the phytase production most. The optimum levels were estimated by Central Composite Design (CCD) of Response Surface Methodology (RSM). The interactive effects of phosphorus sources were found to have significant effect on phytase yield. Application of Genetic Algorithm (GA)/Nelder-Mead Downhill Simplex (NMDS) with RSM model was proved to be more efficient approach for optimization of phytase production by Rhizopus oryzae. A 7.95-fold increase in phytase production (12640 ± 1450 Ul-1) was achieved at the GA-predicted optimum concentration of (gl-1); mannitol 22.8, K2HPO4 5.18, Na2HPO4 3.25, and sodium phytate 9.68, compared with the phytase yield before optimization (1589 ± 135 Ul-1). In the bioreactor studies, the enzyme yields were sustainable to that of the shake flask however, the time required for maximum phytase production was significantly reduced (288 h to 96 h), resulting in an increase in productivity by 3.32-fold.
| Keywords |
| Rhizopus oryzae; Phytase; Central composite design; Genetic algorithm; Nelder-Mead downhill simplex; Bioreactors |
| Introduction |
| Phytic acid (D-myo-inositol 1,2,3,4,5,6 hexakisphosphate) is the principal source of phosphorus present in cereals, legumes, nuts and oilseeds [1]. Phytase (myo-inositol hexakisphosphate phosphohydrolases), which hydrolyses the phytate, helps in preserving the non-renewable phosphate source by replacing the lavish supplementation of additional phosphates into animal diets to meet their nutritional requirements. Phytase is ubiquitous in a large number of plants, animals and microorganisms, however, the fungal strains are widely recognized as the best phytase producers [2]. Recently, the industrial potential of fungal enzymes has motivated research toward development of processes to improve wild strain. Strain improvement by subsequent heat and cold shock has been attempted for increasing the phytase yield from R. oryzae [3]. Previously, the enhanced phytase production by the use of induced mutagenesis has been reported by Chelius and Wodzinski and Shah et al. [4,5]. |
| With the awareness of the potential adverse effects of unutilized phosphorus in phytate on the health of monogastric animals (poultry and swine), humans and the environment, industrial demand of phytase has been increased tremendously [2,3]. The prerequisite for the success of an industrial fermentation process is to design an appropriate production medium as it directly affects the time and costs of the products. The optimization techniques have been thoroughly studied ranging from traditional One-Factor-At-A-Time (OFAT) method to statistical experimental designs such as Plackett-Burman Design (PBD) and Response Surface Methodology (RSM) [3,6]. PBD is a well established and widely used statistical technique for screening the medium components in shake flasks and mathematically computes the significance of large number of variables in a single experiment. RSM, which includes factorial design and regression analysis, can analyze the effect of several independent variables as well as their interactions. This process utilizes a low order polynomial equation in a predetermined region of independent variables, which is later analyzed to locate the optimum values of the independent variables for the best response. |
| A Genetic Algorithm (GA) is search algorithm for optimisation and is based on Darwinian principle of natural selection “survival of the fittest” strategy to eliminate unfit solutions and uses gene information and chromosome processing to optimize the given function [7]. The great advantage of GA lies in the fact that they do not need the objective function to be continuous, convex or unimodel. Additional ability of GA to handle a wide variety of constraints in the design space makes it an efficient and a flexible method in comparison to the other conventional methods. Successful implementation of this approach for the optimization of response surfaces in order to find the optimum values of the independent variables has rapidly increased in recent years as evident from its application in a wide range of fields [8,9] Nelder-Mead Downhill Simplex (NMDS) is a single-objective optimization approach and is aimed at replacing the best vertex of the simplex with a better one or to confirm that it is suitable for the global optimum [10]. |
| Optimization of culture conditions using statistical tools has been thoroughly investigated in enhancing the phytase production from various microorganisms in Submerged Fermentation (SmF). In this paper, the use of stochastic search procedures based on central composite designs has been employed in an efficacious manner to determine the optimal medium components resulting in a costeffective phytase production process. |
| Present study is a first attempt towards optimizing medium components to maximize phytase production using RSM based models coupled with GA/NMDS. Previous investigation has revealed the production of a potential phytase from wild R. oryzae under Solid State Fermentation (SSF) [3]. In the present study, we have significantly increased the production of phytase from an improved strain of R. oryzae under submerged culture that has not been reported earlier. The study was further extended to higher volume production of phytase in a 7-l fermenter. |
| Materials and Methods |
| Microorganism and phytase production |
| Rhizopus oryzae procured from Microbial Type Culture Collection (MTCC), Chandigarh (India), was subjected to stress conditions according to Rani and Ghosh [3]. The best phytase producing strain was routinely maintained on potato dextrose agar (PDA) (HiMedia, India) slants for 6 days at 30°C and were stored at 4°C. Viable spores from slants were harvested by washing with 0.1% (v/v) Tween 80 and the spore suspension adjusted to ~1×106 colony forming units (CFU) per ml was used as inoculum for subsequent fermentations. The basal medium (50 ml) in 250 ml Erlenmeyer flasks contained (gl-1) glucose 10, peptone 5, and micronutrient salt solution (M/N; NaCl, 1.5; MgSO4.7H2O, 1.5; MnSO4.H2O, 0.05; FeSO4.7H2O, 0.05 and CaCl2.2H2O, 1.5) with pH adjusted to 5.6. The flask was inoculated with 5% inoculum concentration and kept for shaking at 200 rpm at 30°C in a shaker for 14 days. Crude extract was obtained after centrifugation at 10000 g for 15 min in a refrigerated centrifuge. The cell free supernatant was used for phytase activity assay. |
| Statistical optimization of medium components for phytase production |
| PBD was employed for screening the most significant medium components and culture conditions influencing the phytase production most. Based on single-factor experiment for the phytase production, suitable culture conditions and concentration ranges of medium components were determined preliminarily (Table 1). Coefficients of all variables were estimated by subjecting the experimental data to statistical analysis. All experiments were carried out in triplicates and the average of phytase production was taken as response. The variables with p-value<0.001 were considered significant in influencing the phytase production by R. oryzae. |
| A 24 factorial design having sixteen factorial points, eight axial points and six replicates at the centre point with a total number of 30 runs was formulated (Table 2). The following second-order polynomial model Equatation. (1) was used to be fitted to the yield values: |
 (1) (1) |
| where, Y is the observed value of the response; xi (i=1, 2, 3 and 4) is the controlling factors; β0 is the offset term, and βi (i=1, 2, 3 and 4), βii and βij (i=1, 2, 3 and 4; j=2, 3 and 4) are the model linear, quadratic and interaction coefficient parameters, respectively. The phytase activity (Ul-1) was taken as dependent variables or response Y. |
| For GA optimization, the input parameters employed in the present work were selected after several trials of GA simulation. |
| Statistical analysis |
| The statistical software package ‘Design-Expert’ 8.0.6, Stat-Ease Inc., Minneapolis, MN, USA was used for experimental design and subsequent regression analysis of the experimental data. The GA/ NMDS optimizations were implemented in MATLAB v8.0 (Math Works, Inc.). All experiments were performed in triplicate and are represented as mean ± SD. |
| Validation of the experimental model |
| Flask level experiments were carried out under optimum conditions, predicted by the RSM-based GA model. The inoculated flasks were kept on a shaker at 200 rpm for 14 days at 30°C. Samples were drawn at desired intervals, centrifuged at 10000 g for 15 min in a refrigerated centrifuge and were analyzed for phytase activity. |
| The fermenter study for phytase production was carried out in a 7-l fermenter (Bioflo, New Brunswick Scientific, NJ, USA) with 5-l working volume, in aforementioned optimized media. |
| Analytical methods |
| Phytase activity was determined by estimating the inorganic phosphate released from sodium phytate [11]. One unit of phytase is defined as the amount of enzyme required to release 1 nmol of inorganic phosphate (Pi) per second under the standard assay conditions. |
| Results and Discussion |
| PBD was used for investigating the relative importance of thirteen nutritional components for phytase production. The corresponding effects of these factors on phytase activity are shown in Table 3. From the regression analysis, it was evident that A (glucose), C (mannitol), K (yeast extract), L (peptone) and Q (ZnSO4) enhanced the phytase production at their low level whereas, high level of F (sucrose), G (ammonium nitrate), N (KH2PO4), O (K2HPO4), P (Na2HPO4), R (phytate), S (tween 80) and T (M/N) supported high phytase yield. The regression model gave a model F-value of 30.14 with a corresponding model p-value (>F) of 0.0002, that shows the model to be highly significant. Based on individual probability factor of failure (>F), the variables (mannitol (C), K2HPO4 (O), Na2HPO4 (P) and phytate (R) with their corresponding probability less than 0.001 were considered significant (Table 3). |
| The CCD design matrix showing different combinations of mannitol, K2HPO4, Na2HPO4 and phytate along with their corresponding experimental and predicted responses is presented in Table 2. The experimental results were analyzed using analysis of variance (ANOVA) which shows that the regression was statistically significant (P < 0.0001) at 95% of confidence level. The results for ANOVA analysis are summarised in Table 4. Application of multiple regression analysis on the experimental data resulted in the following quadratic model Equatation. (2) explicitly explaining the phytase production as a function of initial values of selected medium components: |
| Phytase activity Y = 13758.21-479.25A-103.75B-787.92C + 960.42D- 275.63AB-749.38AC + 153.13AD + 699.38BC-603.13BD + 1070.63CD-1097.05A2-505.43B2-355.43C2-1242.93D2 (2) |
| where, Y represents phytase activity (Ul-1), and A, B, C and D are the coded factors of mannitol, K2HPO4, Na2HPO4 and sodium phytate, respectively. The statistical significance of the model equation for phytase production was supported by the model high F-value of 18.27. Again, the quality of fit of the regression model was justified by high values of coefficient of determination (R2) of 0.9446, which indicates an excellent correlation between the independent factors. The Coefficient of Variation (CV) indicates the degree of precision with which the treatments are evaluated. Lower value of CV viz. 6.80 demonstrated that the performed experiments were highly reliable and was performed with a better precision. The "Lack of Fit F-value" of 1.81 for phytase production implies that there is a 29.77% chance that a this large could occur due to noise. Furthermore, high values of adequate precision (15.815) that represents signal (response) to noise (deviation) ratio, indicates an adequate signal and suggested that the model can be used to navigate the design space. |
| The significance of each coefficient was determined by t-values and P-values as shown in Table 4. As per the regression analysis performed on the present model for phytase production, it can be seen that the variable with largest effect was the squared terms of mannitol (A2) and sodium phytate (D2). Furthermore, the linear effect of sodium phytate and interaction effects of sodium phytate with Na2HPO4 were most significant factors for phytase production (Table 4). In the present study, enhancing effect of mannitol for maximum phytase production seems counterintuitive as most literature showed glucose, starch or sucrose as the preferred carbon source for phytase production [6]. Earlier, mannitol has been reported to have a role in stress tolerance and spore dispersal [12], hence, presence of mannitol might be having some protective role that resulted in enhanced phytase production. Other interesting finding observed in the present study was the phytase production at an overall high concentration of phosphorus (~0.8%). It might be due to the fact that presence of K2HPO4 and Na2HPO4 together served as a buffer for pH of the media. Most of the studied phytases were reported to be repressed at high phosphorus concentration [4,6]. However, no significant inhibition or stimulation of phytase production was reported by Lan et al. and Fredrikson et al. [13,14]. |
| In order to gain the better understanding of the interaction effects of the significant factors and their optimum concentrations, the predicted model was plotted as 2D contour plots and 3D response curves. Respective response curves, representing an infinite number of combinations of two test variables with the other two maintained at their respective zero levels are presented in Figure 1a-c. The elliptical response surfaces implied that there were perfect interaction between the independent variables, however, the circular surfaces suggested that the optimized values may not vary widely from the single variable conditions. In the present study, the strong interaction effects among different phosphorus sources for phytase production were evident from the plots shown in Figures 1a and 1b. This is further supported by their smaller P-values, suggesting the important role of phosphorus sources in phytase synthesis. Maximum phytase activity in presence of Na2HPO4 and sodium phytate was predicted at their corresponding concentration levels in the range of 0.1-0.3% (w/v) and 0.76-0.8% (w/v), respectively (Figure 1a). No significant interaction effects, as illustrated by the circular contour surfaces, were observed for phytase production, when mannitol was combined with K2HPO4 and sodium phytate, respectively (Figure 1c). The optimum concentration of medium components, calculated from the RSM model Equatation. (2) were (gl-1); mannitol 23, K2HPO4 6.1, Na2HPO4 5.4, and sodium phytate 9.6 respectively. |
| The GA and NMDS were implemented separately to determine the optimum concentrations of the four significant variables. The following reduced model for phytase production as response (Equatation. (3) was used as fitness function in both optimizations. |
| Phytase activity Y=-14.97-1.73C+3.83D-0.075AC+0.35BC+0.53CD- 0.011A2-0.13B2-0.31D2 (3) |
| The maximum fitness function (Phytase activity, Uml-1) was obtained at the combination of slightly lower concentration levels of phosphorus sources as compared to the RSM-predicted ones and were observed to be (gl-1); mannitol 22.8, K2HPO4 5.18, Na2HPO4 3.25, and sodium phytate 9.68, respectively. The optimization using NMDS approach predicted similar optimum combinations of the medium components as that of the GA-based optimization. The function was found to converge to an optimum after 43 iterations. |
| Validation experiments showed a strong agreement between the GA-predicted response (11993.40 Ul-1) (data not shown) and the experimental response (12640 ± 1450 Ul-1), however a significant difference between RSM-predicted response (13746.62 Ul-1) and observed response (10746.85 Ul-1) was observed. The results clearly indicated the high adequacy of the GA-based RSM strategy over RSM leading to a significant increase in phytase yield (7.95-fold) over unoptimized medium. |
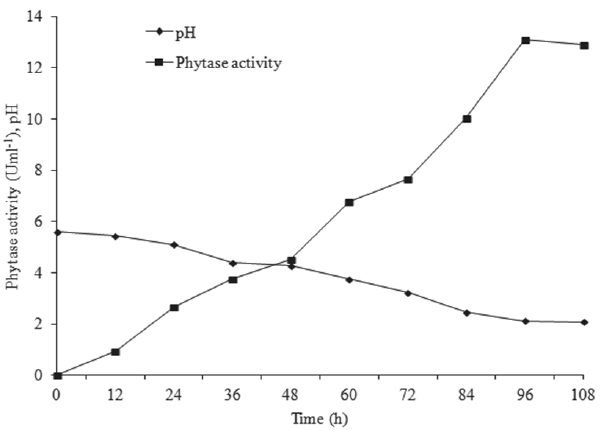
| Phytase production was sustainable in Erlenmeyer flasks of varied volumes (productivity→43.85 ± 0.06 Ul-1h-1) and in fermenter and therefore suggests the feasibility of phytase production at higher volume also. The most significant effect was reduction in fermentation time for maximum phytase production in the fermenter that resulted in an increase in overall productivity from 43.85 to 136.56 Ul-1h-1 (Figure 2). |
| In conclusion, GA/NMDS approach was found to be more efficient in determining the optimum combination of medium components leading to an overall economical production process, in comparison to RSM. The fermenter studies showing an overall increase in phytase productivity by 3.11-fold further supports the reliability as well as the applicability of this optimization tool for higher volume production of phytase. |
References
|
Tables and Figures at a glance
| Table 1 | Table 2 | Table 3 | Table 4 |
Figures at a glance
 |
 |
| Figure 1 | Figure 2 |
Relevant Topics
- Anaerobic Biodegradation
- Biodegradable Balloons
- Biodegradable Confetti
- Biodegradable Diapers
- Biodegradable Plastics
- Biodegradable Sunscreen
- Biodegradation
- Bioremediation Bacteria
- Bioremediation Oil Spills
- Bioremediation Plants
- Bioremediation Products
- Ex Situ Bioremediation
- Heavy Metal Bioremediation
- In Situ Bioremediation
- Mycoremediation
- Non Biodegradable
- Phytoremediation
- Sewage Water Treatment
- Soil Bioremediation
- Types of Upwelling
- Waste Degredation
- Xenobiotics
Recommended Journals
Article Tools
Article Usage
- Total views: 14772
- [From(publication date):
specialissue-2014 - Aug 29, 2025] - Breakdown by view type
- HTML page views : 10071
- PDF downloads : 4701
