Research Article Open Access
Slope Stability and Vegetation
Maria Charlafti*Rail Bridge Engineer, CH2M HILL, London, United Kingdom
- *Corresponding Author:
- Maria Charlafti
Rail Bridge Engineer
CH2M HILL, London-W67EF, United Kingdom
Tel: +44203479 8000
E-mail: mcharlaftis@yahoo.gr
Received July 18, 2014; Accepted November 20, 2014; PublishedNovember 27, 2014
Citation: Charlafti M (2014) Slope Stability and Vegetation. J Archit Eng Tech 3:134. doi:10.4172/2168-9717.1000134
Copyright: © 2014 Charlafti M. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Architectural Engineering Technology
Abstract
This study explores issues related to vegetation effects in slope stability analysis. The main objective of this research was to assess the influences of suction in the stability of slopes. A slope inclination of 1:2 was tested in all cases using SLOPE/W which is sophisticated software with useful features, including suction parameter. Therefore, slope stability analysis was achieved with the usage of this sophisticated software so as to simplify the mathematical processes which are time-consuming. The analysis was based on the Mohr-Coulomb equation arranged appropriately so as to include suction effects. Field measurements recorded by Biddle for mature trees placed on clay subsoil were used to measure the suction effects for each case. Overall, a satisfactory association between field data and results was achieved. For the cases considered, it was indicated that moderately small suction changes from 18 to 39 kPa can influence the safety factor against failure of the slope. All of the analyses showed that the slope model was stable in each case, since safety factor ranged from 1.689 to 4.750. Under undrained conditions Gault clay was found to have a minimum safety factor of 2.553. Suction effects were found to increase the stability of slopes. In the unsaturated analysis, it was found that as jb increased the FOS also increased. Moreover, London clay was found to have a minimum FOS of 2.303 when tested with the effects of matric suction.
Keywords
Slope stability; Vegetation; Suction parameter; Clay subsoil; Geotechnical; Geo-environmental
Introduction
It is well known that the presence of vegetation has an important role in slope stability analysis. It was suggested by Simon and Collison, cited in Ali and Rees [1] that vegetation on slopes can be divided into two categories, mechanical and hydrological. When dealing with geotechnical and geo-environmental problems, soil suction variations are taken into account which may occur in the presence of vegetation and especially on the removal of vegetation. Moreover, the interaction between the plant roots and soil suction is a field which needs to be investigated since they influence the overall shear strength slopes and may cause failure. The relationship between the presence of trees, pore water pressures in embankments and climate with respect to soil moisture deficits was discussed by Ridley et al., cited in Ali and Rees [1].
This study explores the development of a slope model in SLOPE/W, software which not only performs a reliable slope stability analysis, but also considers the effects of suction which may be caused by the presence of vegetation in embankment slopes. Furthermore, the changes in moisture contents throughout seasonal periods are clearly of importance. Therefore, three cases of clays (Boulder Clay, Gault Clay and London Clay) were chosen with the respective trees (Lime, Poplar and Oak) provided by Biddle’s field measured data. In addition, different soil conditions were taken into account. Firstly, an undrained analysis was conducted without the effects of vegetation and then two different cases of unsaturated analysis using a modified form of the Mohr-Coulomb failure criterion. The first unsaturated analysis took into account the effect of matric suction and the second the additional root strength.
Materials and Methods
Undrained analysis for circular slip surfaces
In the first stage of analysis for each case considered, SLOPE/W was used to compute the minimum factor of safety of fully-saturated clays. In order to estimate the minimum factor of safety, undrained analysis was chosen where Φu=0 which means that the clay is purely cohesive and consequently 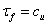 where
where 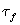 is the shear strength of the soil. Vegetation effects were not taken into account in this type of analysis, since vegetation is correlated with suction and root strength.
is the shear strength of the soil. Vegetation effects were not taken into account in this type of analysis, since vegetation is correlated with suction and root strength.
The fact that clay is purely cohesive under undrained conditions means that no drainage is allowed [2]. According to Craig, circular slips are associated with homogeneous and isotropic conditions of the soil. Failure of the slope could occur because of the weight of the soil above the slip surface. Finally, undrained shear strength (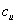 ) was found for the three soil types (Boulder clay, Gault clay and London clay). Due to the fact that the aim of this dissertation is to estimate the minimum safety factor, worst case scenarios were taken into consideration, therefore the worst values of (
) was found for the three soil types (Boulder clay, Gault clay and London clay). Due to the fact that the aim of this dissertation is to estimate the minimum safety factor, worst case scenarios were taken into consideration, therefore the worst values of ( 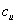 ) were chosen.
) were chosen.
Method of slices (Bishop’s Simplified Method)
Bishop’s simplified method was used to analyse the stability of slopes for the next two stages where the cases of unsaturated clays were taken into account. The assumption made in this method is that the tangential interslice forces are equal and oppose each other thus 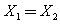 . On the other hand, the normal interslice forces
. On the other hand, the normal interslice forces 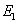 and
and 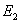 are not equal [3].
are not equal [3].
By resolving forces in the vertical direction where 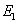 and
and 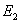 are ignored, the following equation is produced [3]:
are ignored, the following equation is produced [3]:
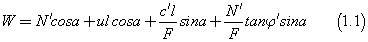
Rearranging the above equation gives:
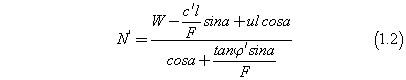
The expression of N’ shown in equation 1.2, can be inserted in equation 1.3, which occurs for homogeneous slopes where the effective cohesion ( 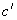 ) and the effective friction of angle (
) and the effective friction of angle (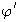 ) are constant along the slip surface.
) are constant along the slip surface.
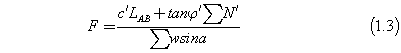
This gives:
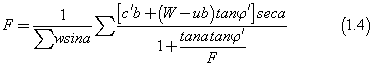
As a result, of the existence of the factor of safety (F) in both sides of the equation 1.4, an iterative process is needed in order to converge to a close estimate of factor of safety. Iterative processes are time consuming; that is why the use of software is commonly used in order to carry out the analysis quickly and reliably.
The correlation of water retention curves with shear strength: The next two stages of the analysis, also included the effect of matric suction since there is an interaction with the root-plant systems, so as to find how shear strength would change when the parameter of matric suction was added in the equation. Fredlund and Rahardjo [4] reported that matric suction is related to the capillary phenomenon which is caused by the surface tension of water. Fredlund et al., cited in Vanapalli et al. [5] suggested a linear
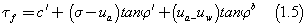
Where 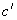 is the effective cohesion,
is the effective cohesion, 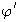 is the effective friction angle,
is the effective friction angle, 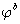 is the angle which describes the increase in shear strength caused by a rise in matric suction [4],
is the angle which describes the increase in shear strength caused by a rise in matric suction [4], 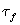 is the shear strength of an unsaturated soil and
is the shear strength of an unsaturated soil and 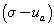 and
and 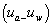 are the net normal stress and the matric suction of the soil on the failure plane at failure. The value of
are the net normal stress and the matric suction of the soil on the failure plane at failure. The value of 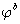 is always equal or less than
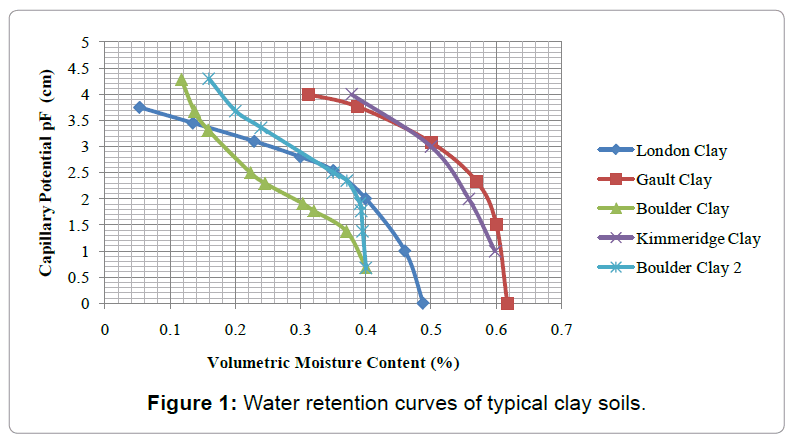
is always equal or less than 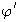 . Moreover, in order to approximate the value of suction due to the presence of vegetation for each case considered, water retention curves for the chosen soil types of clays were illustrated graphically. This helped to correlate matric suction with the volumetric moisture content changes for each soil type, provided by Biddle [6]. In Figure 1, water retention curves for the different soil types chosen for this study are shown in Figure 1.
. Moreover, in order to approximate the value of suction due to the presence of vegetation for each case considered, water retention curves for the chosen soil types of clays were illustrated graphically. This helped to correlate matric suction with the volumetric moisture content changes for each soil type, provided by Biddle [6]. In Figure 1, water retention curves for the different soil types chosen for this study are shown in Figure 1.
In the current work, Boulder Clay-Lime tree, Gault clay-Poplar tree and London clay-Oak tree were chosen to research the influences of matric suction to shear strength according to Mohr-Coulomb failure criterion. For comparison Figure 1 also shows measured data for two other soil types: Boulder clay 2 and Kimmeridge clay. It can be seen that the water retention curves conform to previous published data for this types of soil since water retention curve of gault clay was produced according to Rees [7], boulder clay according to Rees and Ali [8]. Finally, London clay was estimated in a similar way as Gault clay. In addition, the values of moisture contents 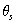 and
and 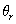 , where the former is the saturated water content whereas the latter is the residual water content, have been taken directly from the measured moisture profiles provided by Biddle [6].
, where the former is the saturated water content whereas the latter is the residual water content, have been taken directly from the measured moisture profiles provided by Biddle [6].
Results
Case study: boulder clay-lime tree
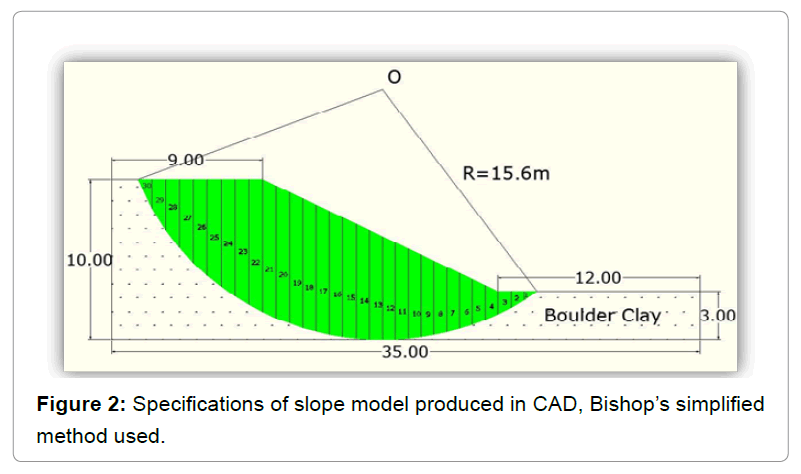
Undrained Analysis without the effect of vegetation: The undrained analysis, also known as total stress analysis, of a fullysaturated boulder clay under undrained conditions was carried out where Φu = 0 and 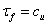 [9]. The assumption made in the analysis is that the soil is homogeneous along the profile of the slope and the topsoil which contains organic content is ignored. The trial slip surface is a circular arc. A circle can be defined by specifying the x-y coordinate of the centre and the radius. A large range of different slip surfaces can be specified by defining the grid limits of circle centres and a number of circle radii [10]. In SLOPE/W, this procedure is called the Grid and Radius method. The undrained slope stability analysis was carried out with the help of Slope/W software. The dimensions of the slope model and the undrained shear strength of the soil were entered in SLOPE/W which examined the safety factor for thousands of possible circular slip surfaces using the Bishop's simplified method of slices (Figure 2).
[9]. The assumption made in the analysis is that the soil is homogeneous along the profile of the slope and the topsoil which contains organic content is ignored. The trial slip surface is a circular arc. A circle can be defined by specifying the x-y coordinate of the centre and the radius. A large range of different slip surfaces can be specified by defining the grid limits of circle centres and a number of circle radii [10]. In SLOPE/W, this procedure is called the Grid and Radius method. The undrained slope stability analysis was carried out with the help of Slope/W software. The dimensions of the slope model and the undrained shear strength of the soil were entered in SLOPE/W which examined the safety factor for thousands of possible circular slip surfaces using the Bishop's simplified method of slices (Figure 2).
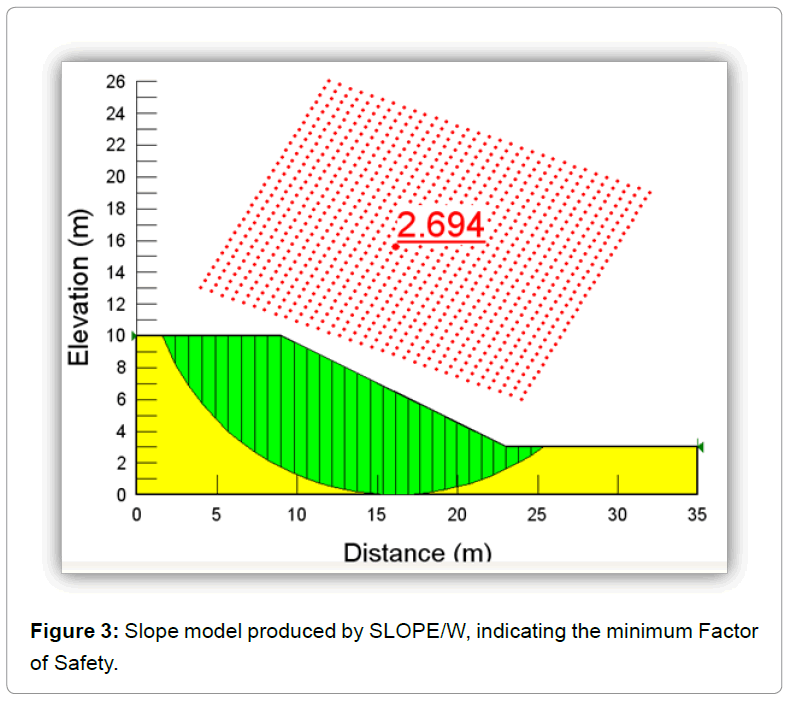
Slope/W produced 49011 different slip circles, divided in 30 slices. The critical slip circle has a factor of safety of 2.694 according to the Bishop method of slices (Figure 3). The detailed results for critical slip surface are shown in SLOPE/W report (boulder clay-undrained analysis) in Appendix A. Slip surfaces within the soil were expected to have a high factor of safety because the soil has a high undrained shear strength (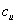 ) of 65kN/ m2 (Figure 3).
) of 65kN/ m2 (Figure 3).
Analysis of unsaturated boulder clay including the effect of matric suction: This analysis covers the case of unsaturatedboulder clay. The assumption made in the analysis is that the soil is homogeneous along the profile of the slope and the top-soil which contains organic content is ignored. The dimensions of the slope model remained the same. The unit weight of the soil ![]() , the effective cohesion (
, the effective cohesion (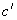 =9.6), effective friction of angle (
=9.6), effective friction of angle ( 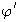 =27.3) and
=27.3) and 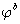 =21.7, parameter of the soil were entered in the software. Material properties of Boulder Clay were taken from Ali and Rees [1]. From a slope stability analysis point of view, effective strength parameters give the most realistic solution, regarding the location of the critical slip surface. The critical slip surface position predicted is more realistic when effective strength parameters are used. SLOPE/W assumed that
=21.7, parameter of the soil were entered in the software. Material properties of Boulder Clay were taken from Ali and Rees [1]. From a slope stability analysis point of view, effective strength parameters give the most realistic solution, regarding the location of the critical slip surface. The critical slip surface position predicted is more realistic when effective strength parameters are used. SLOPE/W assumed that 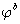 is constant, but in reality
is constant, but in reality 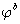 changes with the degree of saturation. When the soil is saturated,
changes with the degree of saturation. When the soil is saturated, 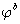 is equal to the effective friction angle
is equal to the effective friction angle 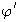 , as the pore-water pressure in the capillary zone is under tension [10]. As the soil desaturates,
, as the pore-water pressure in the capillary zone is under tension [10]. As the soil desaturates, 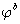 decreases. Furthermore,
decreases. Furthermore, 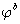 is correlated to the SWCC which is also known as the volumetric water content function. It was noted that the most realistic position of the critical slip surface is obtained when effective strength parameters are used in the slope stability analysis. Effective strength parameters, however, are only meaningful when they are used in conjunction with pore-water pressures. The most common way of defining pore-water pressure conditions is with a piezometric line, where SLOPE/W calculates the vertical distance between the piezometric line and the middle of the base of the slice. It then calculates the product of this vertical distance and the unit weight of the water, so as to obtain the magnitude of pore water pressure at the base of each slice. Therefore, a piezometric line was chosen in the program which was located in the lower bound of the slope model [10]. Therefore, the effect of the piezometric line does not affect the analysis because it is considered to be negligible. In addition, the effect of suction estimated from Biddle’s field data for seasonal (and persistent) deficits of moisture content at 1.4m and 5.6m distance from tree was added to the program. The value of matric suction was found to be 20 kPa. The water retention curve was determined by using the van Genuchten’s method [1]. The relationship corresponding to this method is expressed as:
is correlated to the SWCC which is also known as the volumetric water content function. It was noted that the most realistic position of the critical slip surface is obtained when effective strength parameters are used in the slope stability analysis. Effective strength parameters, however, are only meaningful when they are used in conjunction with pore-water pressures. The most common way of defining pore-water pressure conditions is with a piezometric line, where SLOPE/W calculates the vertical distance between the piezometric line and the middle of the base of the slice. It then calculates the product of this vertical distance and the unit weight of the water, so as to obtain the magnitude of pore water pressure at the base of each slice. Therefore, a piezometric line was chosen in the program which was located in the lower bound of the slope model [10]. Therefore, the effect of the piezometric line does not affect the analysis because it is considered to be negligible. In addition, the effect of suction estimated from Biddle’s field data for seasonal (and persistent) deficits of moisture content at 1.4m and 5.6m distance from tree was added to the program. The value of matric suction was found to be 20 kPa. The water retention curve was determined by using the van Genuchten’s method [1]. The relationship corresponding to this method is expressed as:
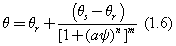
Where 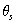 and
and 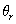 are the saturated and residual water content respectively, m, n and a are shape parameters gained from experience and
are the saturated and residual water content respectively, m, n and a are shape parameters gained from experience and 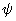 is the capillary potential [8]. Capillary potential
is the capillary potential [8]. Capillary potential 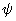 is usually expressed as a negative head of water. pF scale is the Log10 of
is usually expressed as a negative head of water. pF scale is the Log10 of 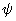 where
where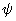 is given in centimeter’s. The link between
is given in centimeter’s. The link between 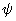 and s is then given by: (Figure 4)
and s is then given by: (Figure 4)
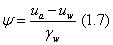
As it can be seen in Figure 4, 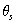 was taken as 0.4 in order to keep one end of the water retention curve fixed. The residual water content was predicted based on other measured data for clay soils [8]. From Biddle’s field experiments it was found that
was taken as 0.4 in order to keep one end of the water retention curve fixed. The residual water content was predicted based on other measured data for clay soils [8]. From Biddle’s field experiments it was found that 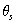 occurred at approximately 42% of moisture content and
occurred at approximately 42% of moisture content and 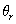 at about 27.5% at 0.5 m depth. Measurements were for 1.0 m and 1.5 m respectively due to the fact that suction mainly influences the soil near the surface where the roots are presented as well. Therefore, these values taken from Biddle’s data were imported into the water retention curve of boulder clay respectively and capillary potential was estimated for each case.
at about 27.5% at 0.5 m depth. Measurements were for 1.0 m and 1.5 m respectively due to the fact that suction mainly influences the soil near the surface where the roots are presented as well. Therefore, these values taken from Biddle’s data were imported into the water retention curve of boulder clay respectively and capillary potential was estimated for each case.
Suction values were estimated for the two cases of Biddle’s data at 0.5 m, 1.0 m and 1.5 m and then an average from both of the two cases was used as for the final suction used in the calculations for evaluation of shear strength. Negative water pressures have the effect of adding strength to a soil. In the same way that positive pore water pressures reduce the effective stress and thereby decrease the strength, negative pore-water pressures raise the effective stress and in turn increase the strength [10].
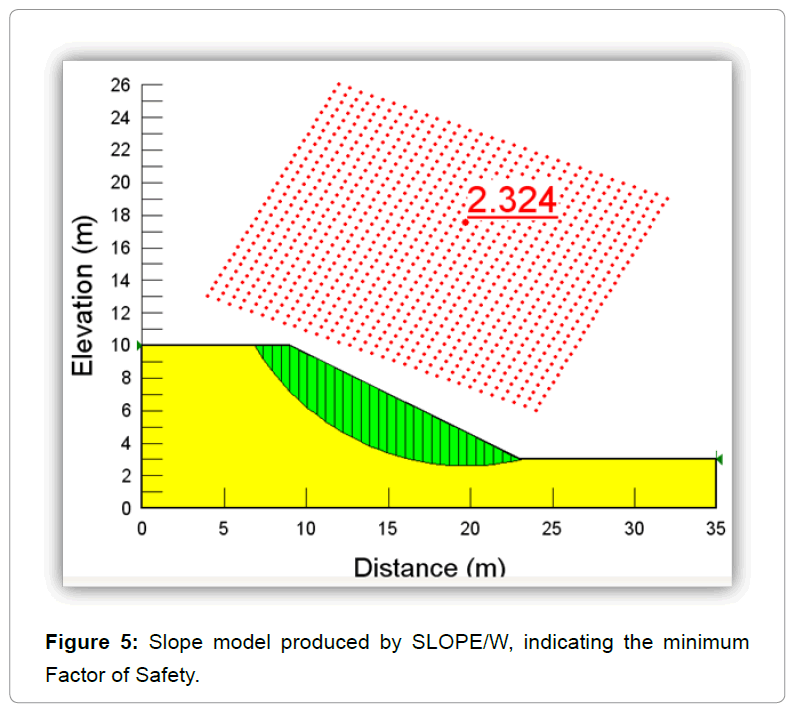
SLOPE/W examined the factor of safety for thousands of possible circular slip surfaces using the Bishop's simplified method of slices. Slope/W produced 49011 different slip circles, divided in 30 slices. The critical slip circle has a factor of safety of 2.324 according to the Bishop method of slices (Figure 5). In addition, the shear strength was obtained to be 40.3 kN / m2 (Figure 5).
Case study: Gault clay-poplar tree
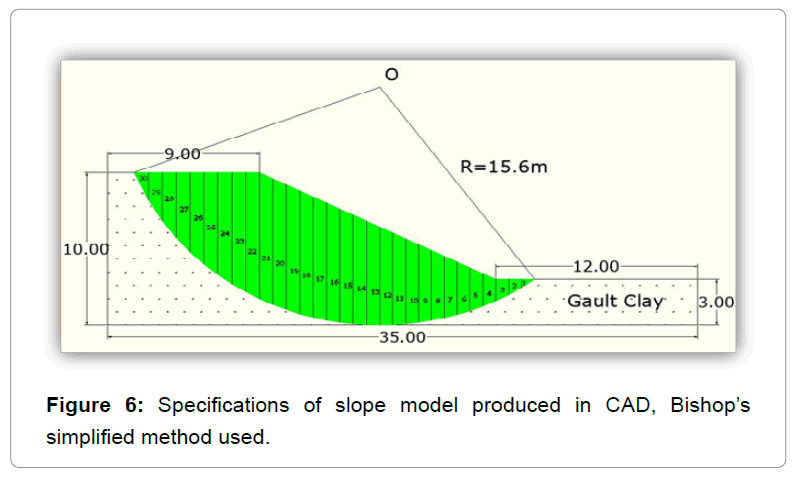
Undrained analysis without the effect of vegetation: Similarly, the undrained analysis of a fully-saturated gault clay under undrained conditions was carried out, where Φu=0 and 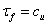 [9]. Shear strength of unweathered gault clay was equal to the undrained shear strength which was equal to 56 kPa under worst case conditions since the minimum Factor of Safety needs to be evaluated [11]. The same assumptions were made thus a homogeneous gault clay along the profile of the slope was examined. Moreover, the undrained slope stability analysis was carried out with the help of Slope/W software. The dimensions of the slope model and the undrained shear strength of the soil were entered in the software. SLOPE/W examined the safety factor for thousands of possible circular slip surfaces using the Bishop's simplified method of slices (Figure 6).
[9]. Shear strength of unweathered gault clay was equal to the undrained shear strength which was equal to 56 kPa under worst case conditions since the minimum Factor of Safety needs to be evaluated [11]. The same assumptions were made thus a homogeneous gault clay along the profile of the slope was examined. Moreover, the undrained slope stability analysis was carried out with the help of Slope/W software. The dimensions of the slope model and the undrained shear strength of the soil were entered in the software. SLOPE/W examined the safety factor for thousands of possible circular slip surfaces using the Bishop's simplified method of slices (Figure 6).
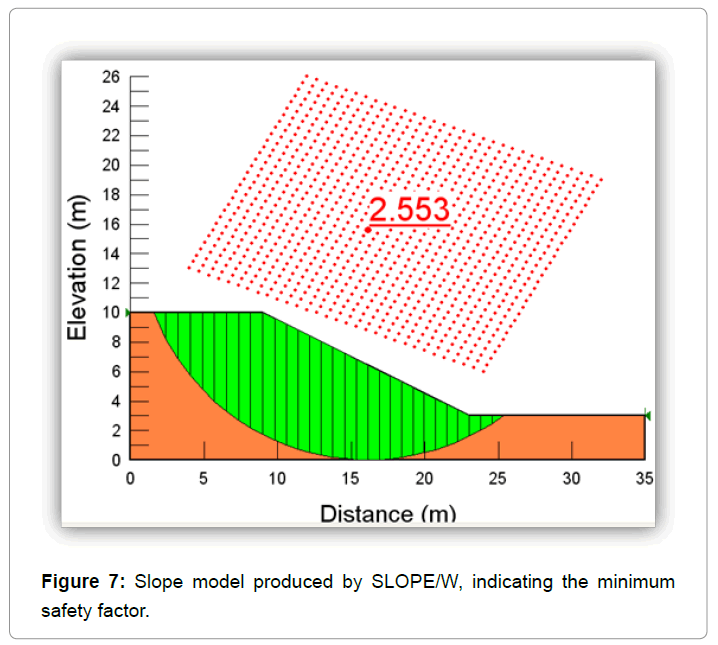
The critical slip circle has a factor of safety of 2.553 according to the Bishop method of slices (Figure 7).
Analysis of unsaturated Gault Clay including the effect of matric suction: This analysis covers the case of unsaturated gault clay. The same assumptions were made for this specific analysis as in previous section. The dimensions of the slope model remained the same and the unit weight of the soil 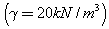 m3), the effective cohesion ( =25), effective friction of angle(
m3), the effective cohesion ( =25), effective friction of angle( ![]() =25) and the angle of shearing resistance with regard to soil suction,
=25) and the angle of shearing resistance with regard to soil suction, 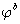 which ranged from 16 to 23 degrees were entered in the software. Material properties of unweathered Gault Clay for worst case conditions were taken from Bell [11]. Moreover, a parametric study for
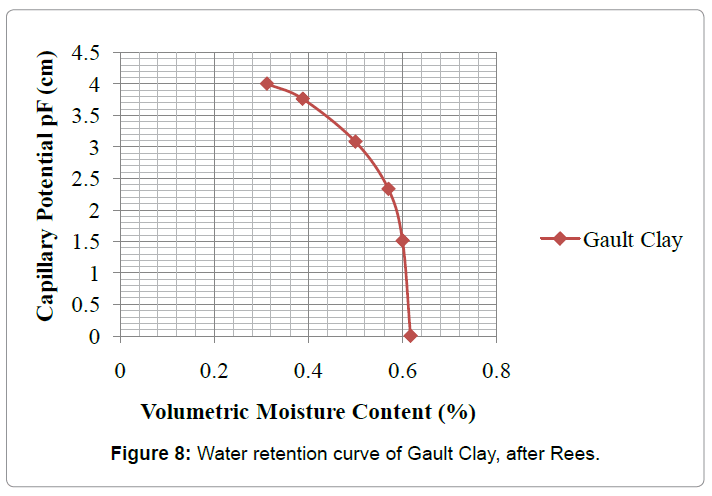
which ranged from 16 to 23 degrees were entered in the software. Material properties of unweathered Gault Clay for worst case conditions were taken from Bell [11]. Moreover, a parametric study for 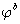 parameter was conducted since a minimum, an average and a maximum value of it were taken. As a result, three cases for the effect of matric suction were examined with the help of SLOPE/W in order to define the effects of it in stabilityanalysis with the presence of vegetation. Furthermore, the effect of suction estimated from Biddle’s field data for seasonal (and persistent) deficits of moisture content at 4.2 m distance from tree was added to the program. The overall value of matric suction was found to be 39 kPa according to (Figure 8).
parameter was conducted since a minimum, an average and a maximum value of it were taken. As a result, three cases for the effect of matric suction were examined with the help of SLOPE/W in order to define the effects of it in stabilityanalysis with the presence of vegetation. Furthermore, the effect of suction estimated from Biddle’s field data for seasonal (and persistent) deficits of moisture content at 4.2 m distance from tree was added to the program. The overall value of matric suction was found to be 39 kPa according to (Figure 8).
From Biddle’s field experiments was found that ( 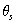 ) occurred at approximately 37% of moisture content and (
) occurred at approximately 37% of moisture content and (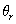 ) at about 21.5% at 0.5 m depth. Measurements were for 1.0 m and 1.5 m respectively due to the fact that suction mainly influences the soil near the surface where the roots are presented as well. Therefore, these values taken from Biddle’s data were imported into the water retention curve of gault clay respectively and capillary potential was estimated for each case (Figure 8). Since y-axis of the water retention curve is logarithmic a conversion of capillary potential to suction needed to be done. Therefore, by converting capillary potential into suction, a value of 39 kPa was estimated for suction.
) at about 21.5% at 0.5 m depth. Measurements were for 1.0 m and 1.5 m respectively due to the fact that suction mainly influences the soil near the surface where the roots are presented as well. Therefore, these values taken from Biddle’s data were imported into the water retention curve of gault clay respectively and capillary potential was estimated for each case (Figure 8). Since y-axis of the water retention curve is logarithmic a conversion of capillary potential to suction needed to be done. Therefore, by converting capillary potential into suction, a value of 39 kPa was estimated for suction.
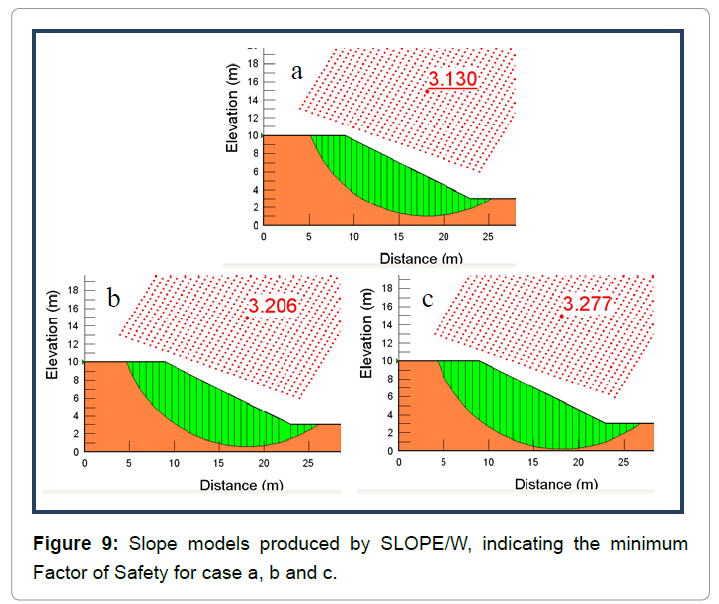
Suction values were estimated for the chosen case of Biddle’s data at 0.5 m, 1.0 m and 1.5 m and then an average was found as for the final suction used in the calculations for the estimation of shear strength. The critical slip circles defined by the program are shown in the following Figure 9, as well as, the minimum factors of safety for each case (Figure 9).
The values of shear strength computed for case a, b and c and are shown in Table 1:
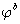 (degrees) (degrees) |
Shear Strength, t (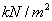 ) ) |
|
|---|---|---|
| Case a | 16 | 54.84 |
| Case b | 19.5 | 57.46 |
| Case c | 23 | 60.21 |
Table 1: Shear strength estimated for the three cases using Mohr-Coulomb equation.
Case study: London clay-oak tree
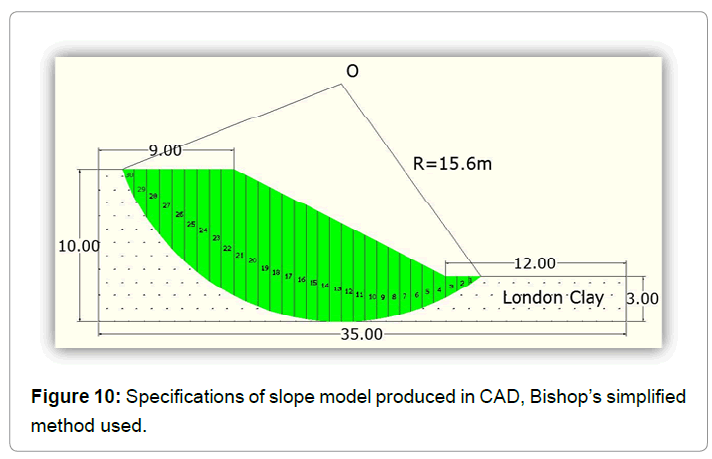
Undrained analysis without the effect of vegetation: The undrained analysis of a fully-saturated London clay under undrained conditions was carried out, where Φu = 0 and 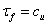 [9]. The same procedure as in previous sections was followed. The shear strength of unweathered London clay was found to be equal to 100kPa according to Bell [11] (Figure 10).
[9]. The same procedure as in previous sections was followed. The shear strength of unweathered London clay was found to be equal to 100kPa according to Bell [11] (Figure 10).
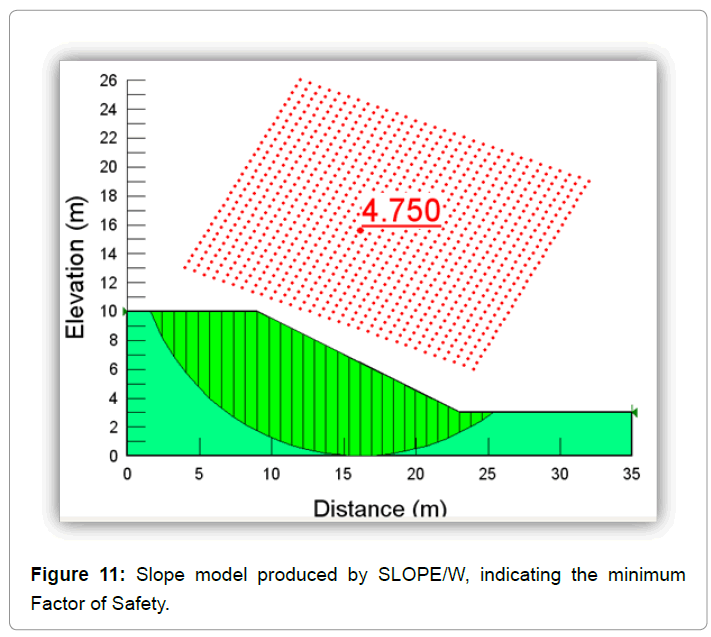
The critical slip circle has a factor of safety of 4.750 according to the Bishop method of slices (Figure 11).
Analysis of unsaturated London Clay including the effect of matric suction: This analysis covers the case of unsaturated London clay. The same assumptions were made for this specific analysis as in previous section. The dimensions of the slope model remained the same and the unit weight of the soil 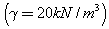 , the effective cohesion (
, the effective cohesion (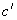 =17) , effective friction of angle (
=17) , effective friction of angle (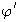 =25) and the angle of shearing resistance with regard to soil suction,
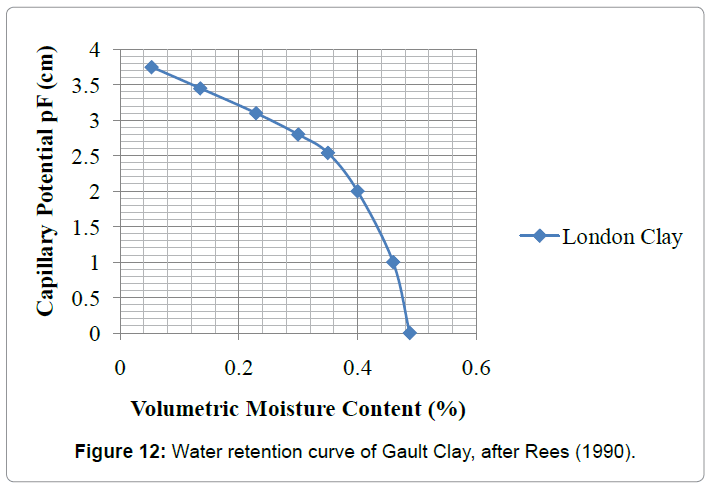
=25) and the angle of shearing resistance with regard to soil suction, 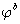 which ranged from 16 to 23 degrees were entered in the software. Material properties of unweather London Clay for worst case conditions were taken from Bell [11]. The same procedure was followed as in previous section. The effect of suction estimated from Biddle’s field data for seasonal (and persistent) deficits of moisture contents at 4.0 m and 8.0 m distance from tree were added to the program. The overall value of matric suction was found to be 18 kPa according to Figure 12.
which ranged from 16 to 23 degrees were entered in the software. Material properties of unweather London Clay for worst case conditions were taken from Bell [11]. The same procedure was followed as in previous section. The effect of suction estimated from Biddle’s field data for seasonal (and persistent) deficits of moisture contents at 4.0 m and 8.0 m distance from tree were added to the program. The overall value of matric suction was found to be 18 kPa according to Figure 12.
From Biddle’s field experiments at 4.0 m and 8.0 m distance from the oak tree was found that( 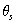 ), occurred at approximately 49.5% of moisture content,(
), occurred at approximately 49.5% of moisture content,(![]() ) at about 35.4% at 0.5 m depth and 51.3% and 39.3% respectively. Measurements were taken for 1.0 m and 1.5 m respectively for both of the two cases due to the fact that suction mainly influences the soil near the surface where the roots are presented as well.
) at about 35.4% at 0.5 m depth and 51.3% and 39.3% respectively. Measurements were taken for 1.0 m and 1.5 m respectively for both of the two cases due to the fact that suction mainly influences the soil near the surface where the roots are presented as well.
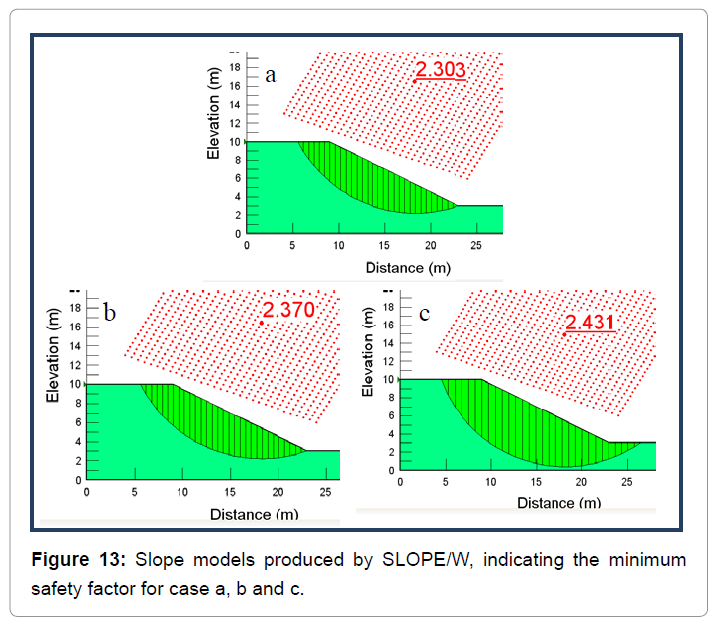
Suction values were estimated for the chosen case of Biddle’s data at 0.5 m, 1.0 m and 1.5 m and then an average was found as for the final suction used in the calculations for the estimation of shear strength. The critical slip circles defined by the program are shown in the following Figure 13, as well as, the minimum factors of safety for each case (Figure 13).
The values of shear strength computed for case a, b and c and are shown in the following Table 2.
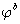 (degrees) (degrees) |
Shear Strength, t (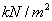 ) ) |
|
|---|---|---|
| Case a | 16 | 36.14 |
| Case b | 19.5 | 37.35 |
| Case c | 23 | 38.62 |
Table 2: Shear strength estimated for the three cases using Mohr-Coulomb equation.
Conclusion and Discussions
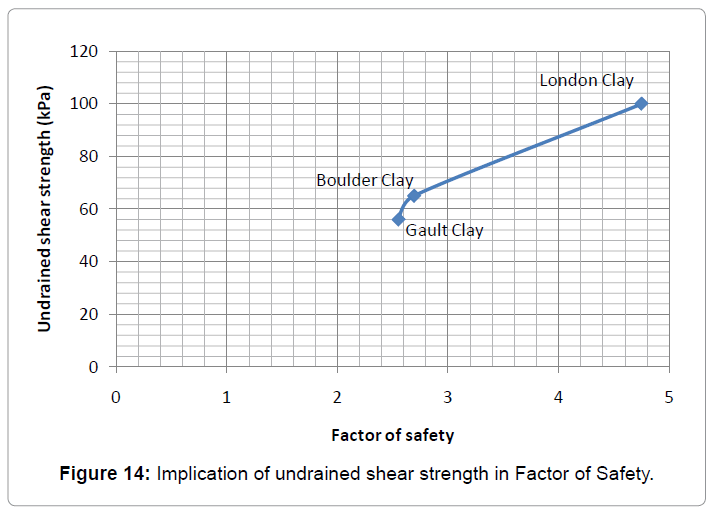
Results of this study were analyzed with respect to the changes in factors of safety, variations in ?b parameter values taken. Three cases were examined for different types of trees and soil types and the results produced showed the significance of matric suction in slope stability analysis under vegetation effects. In order to make it possible to make comparisons of the results, three clay types of soil were chosen (Figure 14).
Figure 14 shows the variations of factor of safety with respect to the undrained shear strength of each soil. It can be said that, the greater the undrained shear strength is the greater is the factor of safety. In addition, it is observed that, boulder and gault clay have very close factor of safety as a result of the very close value of undrained shear strength whereas London clay has a great increase in factor of safety due to very high undrained shear strength (Figure 15).
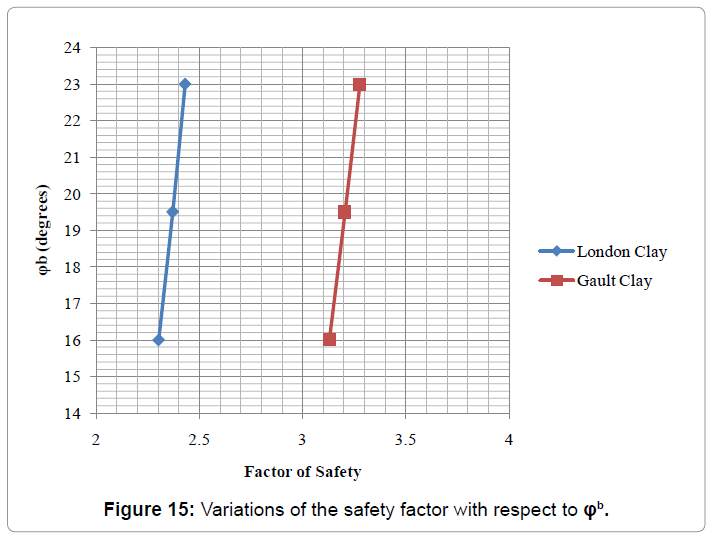
Figure 15 shows the variation of the safety factor according to the different values of ?b taken. It is observed that both London and gault clay have the same increase in ?b parameter whereas the increase in factor of safety is less in London clay with respect to gault clay. This occurs because the effective cohesion and suction value of London clay is less than in gault clay. Therefore, factor of safety of London clay is smaller than in gault clay (Figure 16).
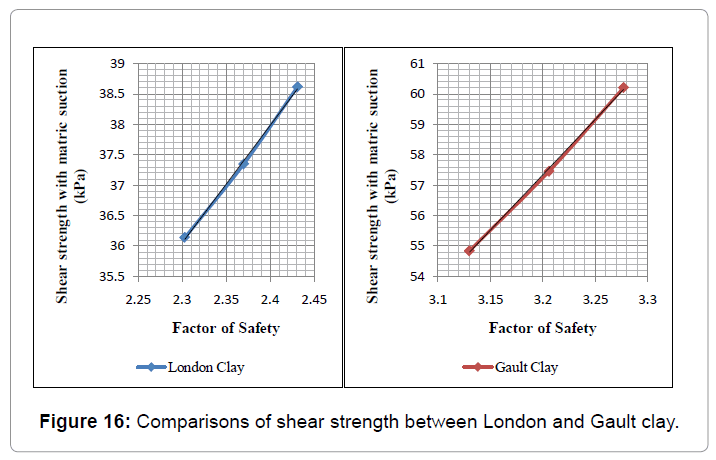
Figure 16 shows the changes of the safety factor with regard to the changes in shear strength. By drawing the best fit line, it can be said that a nearly linear relationship between the FOS and the shear strength exists. The smaller the shear strength is the less is the factor of safety for each of the two soil types. Furthermore, comparing case a and b, a percentage difference in ?b of 21.875% was found which reflects to a percentage difference in factor of safety of 2.909%. Moreover, by comparing case b and c, a percentage difference of 17.948% in 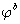 which reflects to a percentage difference of 2.573% in factor of safety. Finally, for the cases a and c, a percentage difference of 43.75% was found which reflects to a percentage difference of 5.557% in factor of safety. In addition, with respect to Gault clay by comparing case a and b, a percentage difference of 21.875% in
which reflects to a percentage difference of 2.573% in factor of safety. Finally, for the cases a and c, a percentage difference of 43.75% was found which reflects to a percentage difference of 5.557% in factor of safety. In addition, with respect to Gault clay by comparing case a and b, a percentage difference of 21.875% in 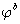 parameter, this reflects to a percentage difference of 2.428% in factor of safety, respectively. Similarly, for case b and c, a percentage difference of 17.948% in ?b reflects to a percentage difference of 2.214% in factor of safety. Finally, for cases a and c, a percentage difference a percentage difference of 43.75% was found which reflects to a percentage difference of 4.696% in factor of safety (Figure 17).
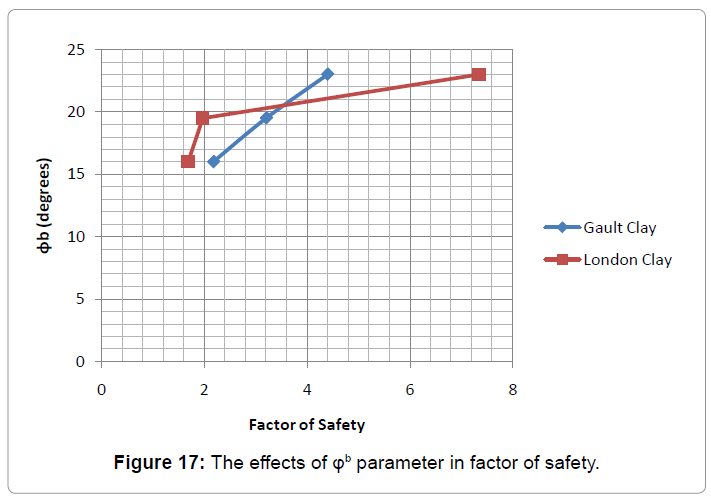
parameter, this reflects to a percentage difference of 2.428% in factor of safety, respectively. Similarly, for case b and c, a percentage difference of 17.948% in ?b reflects to a percentage difference of 2.214% in factor of safety. Finally, for cases a and c, a percentage difference a percentage difference of 43.75% was found which reflects to a percentage difference of 4.696% in factor of safety (Figure 17).
In Figure 17, it can be observed that as ?b increases the factor of safety increases as well, for both of the two soil types. Moreover, it can be observed that there is a linear relationship between ?b and factor of safety in gault clay whereas in London clay is not. In addition, at ?b equal to 16 and 19.5 degrees the factor of safety of gault clay is higher than London clay but at 23 degrees London clay has a greater factor of safety in comparison to gault clay.
Recommendations for Further Research
It was concluded, that vegetation plays an important role in slopestabilisation. Although, it is a complex issue since there are various areas of uncertainties when it comes to engineering problems. Estimations of factor of safeties cannot be precise since there are many aspects of vegetation that are not taken into account in this research such as weight of vegetation and wind loading. However, various outcomes were produced by the work done in regards with matric suction due to presence of vegetation on site. More specifically, three cases were examined, Boulder clay- Lime tree, Gault clay-Poplar tree and lastly London clay- Oak tree. Soil suction had an impact on a limited increase in the safety factor. In addition, it can be said that vegetation helps in reducing the pore water pressure. Vegetation also varied seasonally thus affecting suctions. It was found that suctions for all types of trees were low during the period from late autumn to late spring. Therefore, stabilisation of slopes comes from root reinforcement in wetter periods of time rather than soil moisture reduces. Actually, the above information is an important issue so as to choose the right plant species [12]. Moreover, for all cases examined, the minimum safety factor was found to be 1.689 occurring in the third case of London clay-Oak tree. Therefore, all slopes examined under different conditions were found to be stable since it is suggested by geotechnical engineers that safety factors between 1.10 and 1.30 are potentially unstable thus some protection in order to prevent slope from failing is needed [13]. More specifically, for all the three species and soil types under undrained conditions, the slope model tested and was found to stable with a minimum safety factor of 2.553 which occurred in gault clay. This can be explained by the high undrained shear strengths of the soils. On the other hand, when unsaturated conditions were taken into account for the second and third case of analyses of each case, it was noticed that the maximum changes in matric suctions based on the moisture contents provided by Biddle [6] were found to occur at 0.5m depth. Furthermore, for each case examined, it was proved that the slopes are stable since a minimum factor of safety of 2.303 occurred in the case of London clay-Oak tree. It can be observed that as 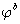 parameter increases, the more the shear strength increases and as a result the safety factor increases as well. However, the changes between shear strength and factors of safety were not so high. A percentage difference of 5.557% between minimum and maximum values of
parameter increases, the more the shear strength increases and as a result the safety factor increases as well. However, the changes between shear strength and factors of safety were not so high. A percentage difference of 5.557% between minimum and maximum values of 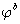 (16 and 23 degrees) was found considering the case of London clay-Oak tree. However, this was not expected since the effective strength parameters and suction value of gault clay-Poplar tree case were higher.
(16 and 23 degrees) was found considering the case of London clay-Oak tree. However, this was not expected since the effective strength parameters and suction value of gault clay-Poplar tree case were higher.
The Following Topics are Recommended for Future Research
• Position of a tree (middle, toe or top of a slope) or a plant is a very important issue since it can affect the slope stability in a significant way with respect to real root architecture for each species [14].
• Another parameter which needs to be investigated is the effect of wind to which vegetation is exposed. Wind loading provides a pressure to vegetation and forces are transmitted to the soil thus reducing its resistance to failure [15].
• Surcharge which arises from the weight of vegetation on the soil has a significant effect on the stability of a slope. Normally, shrubs and grasses in comparison to trees have a smaller effect in slope stabilization. Moreover, weight of vegetation covering the soil, increases the downslope forces and as result lowering the resistance of the soil mass to sliding but it also increases the frictional resistance of the soil [15].
• Additional important factors such as climate changes, rainfalls, and chemical properties of the soil, as well as, physical properties, and plant ages, soil temperature and precipitation which play a significant role on plant growth need to be investigated [16]. Therefore, models which take into account the impact of vegetation need to be designed accordingly.
Acknowledgements
I am thankful to Dr. Steve Rees and Cardiff University for the valuable guidance and encouragement to publish my 3rd year thesis work.
Last but not least, I would like to express my gratitude to Mr. Samer El-Jouzi and CH2M HILL for funding and supporting my work.
References
- AliN, Rees SW (2008)Preliminary Analysis of Tree-induced Suctions on SlopeStability. 1st European Conference on Unsaturated Soils (E-UNSAT 2008). Durham,United Kingdom.
- AndersonMG, Richards KS (1987) Slope Stability: Geotechnical Engineering andGeomorpholpgy. Chichester: John Wiley & Sons.
- BarnesGE (2000) Soil Mechanics: Principles and practice. (2ndedn). Basingstoke:Palgrave.
- FredlundDG, Rahardjo H (1993) Soil mechanics for unsaturated soils. New York: John Wiley & Sons, Inc.
- VanapalliSK, Fredlund DG, Pufahl DE, Clifton AW (1996) Model for the prediction of shearstrength with respect to soil suction. Canadian Geotechnical Journal33:379-392.
- BiddlePG (1998) Tree Root Damage to Buildings. Wantage: Willowmead Publishing Ltd.
- ReesSW (1990) Seasonal Ground Movement Effects on Buried Services. PhD Thesis,Cardiff University.
- ReesSW, Ali N (2006) Seasonal water uptake near trees: a numerical and experimentalstudy. Geomechanics and Geoengineering: An International Journal 1:129-138.
- CraigRF (2004) Craig's Soil Mechanics. 7th ed., New York: Spon Press.
- GEO-SLOPEInternational Ltd (2008) Stability Modeling with SLOPE/W 2007 Version. Calgary:GEO-SLOPE International Ltd.
- Bell FG (2000)Engineering properties of soils and rocks. 4th ed. Oxford: Blackwell ScienceLtd.
- MacNeil DJ (2001) Vegetation for slope stability. TRL Report 515.TRL Limited.
- HubbleTCT (2010) Improving the stream of consciousness: A nomenclature for describingthe factor of safety in river bank stability analysis. Ecological Engineering36:1765-1768.
- GenetM, Stokes A, Fourcaud T, Norris JE (2010) The influence of plant diversity onslope stability in a moist evergreen deciduous forest. Ecological Engineering36:265-275.
- MorganRPC,Rickson RJ (1995) Slope stabilization and erosion control: a bioengineeringapproach. London.
- StokesA,Sotir R, Chen W, Ghestem M(2010) Soil bio- and eco-engineering in China: pastexperience and future priorities. Ecological Engineering 36:247-257.
Relevant Topics
- Architect
- Architectural Drawing
- Architectural Engineering
- Building design
- Building Information Modeling (BIM)
- Concrete
- Construction
- Construction Engineering
- Construction Estimating Software
- Engineering Drawing
- Fabric Formwork
- Interior Design
- Interior Designing
- Landscape Architecture
- Smart Buildings
- Sociology of Architecture
- Structural Analysis
- Sustainable Design
- Urban Design
- Urban Planner
Recommended Journals
Article Tools
Article Usage
- Total views: 17537
- [From(publication date):
December-2014 - Aug 09, 2025] - Breakdown by view type
- HTML page views : 12614
- PDF downloads : 4923