Special Issue Article Open Access
Stochastic Non-Linear Optimization of Equipment Productivity in Multi-Seam Formations
Elijah Adadzi* and Samuel FrimpongMissouri University of Science and Technology, USA
- *Corresponding Author:
- Elijah Adadzi, Professor
Missouri University of Science and Technology
USA
E-mail: ea7t8@mst.edu
Received Date: January 15, 2013; Accepted Date: January 17, 2013; Published Date: January 26, 2013
Citation: Adadzi E, Frimpong S (2013) Stochastic Non-Linear Optimization of Equipment Productivity in Multi-Seam Formations. J Powder Metall Min S1:001. doi: 10.4172/2168-9806.S1-001
Copyright: © 2013 Adadzi, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Powder Metallurgy & Mining
Abstract
The deployment of large mining equipment has resulted in low-cost, high efficiency and bulk production
operations in surface mines. In strip coal mining operations, these economies of scale favor increasingly the use of draglines, shovels, dozers and other support equipment for overburden and coal extraction. However, the selection of particular equipment units, with fixed design geometry, might be economically inefficient in varying geological and operating domains. This study formulates stochastic-optimization (SOP) models of the dynamics of resource allocation in multi-seam deposits. The SOP model maximizes the productivities of draglines as well as other ancillary excavation operations, and determines optimal blends of coal products. Future uncertainties are also characterized for a comprehensive risk modeling and analysis. Application of the SOP model is presented with a bituminous coal mining case. The results show a 3.51% improvement in mining cost and 0.19% increment in net present value. This approach optimizes equipment scheduling in strip mines and ensures high economic efficiencies.
Keywords
Strip mining operations; Multi-seam coal mining; Dragline productivity; Non-linear programming; Stochastic processes; Waste excavation planning; Coal seam extraction
Introduction
The upsurge in surface coal production can be attributed to the advent of larger trucks, shovels and draglines. This growth has resulted in higher production efficiencies [1]. In strip mines, draglines have extensively been engaged for overburden removal due to their economic advantages as compared to other extraction methods. A significant portion (48.32%) of the overall mining cost in strip mines is the cost of waste material extraction (MAC, 2005). Similarly, in terms of equipment energy consumption, waste excavation and material spoiling are the most costly and energy-consuming sectors [2]. This paper focuses on the long-term equipment productivity improvement. The objective is to develop stochastic-optimization models that capture the dynamics of resource allocation in complex multi-seam formations (MSFs). The main modules include
(i) Non-linear programming (NLP) formulations for equipment allocation and material extraction scheduling
(ii) stochastic-optimization models
(iii) Simulation techniques to evaluate different scenarios
(iv) Comprehensive risk analysis of the optimal solutions
The constraint functions incorporate the general geometry of excavation in MSFs as well as equipment operating mechanisms. The following conversation presents the detailed problem definition followed by comprehensive literature on NLP model sand stochastic processes, MSF excavation and its mathematical models and the SOP models. The analysis of the results, major conclusions and future research directions are presented at the end.
Problem definition
The dragline reach and geometry require mining method variations to achieve production targets in complex geologic formations. With increasing overburden depth, rehandling of spoiled material may occur as a result of shorter dragline reach. Mine plans may also specify material schedules and sequencing that might require frequent movement of large equipment. Equipment utilization is reduced due to the frequency and the length of long deadheading periods. On the average, draglines take a step of approximately 6.56 feet within a period of 0.75-1 minute [3]. The dynamics of material dumping is conditioned by the available spoiling area, operational safety, environmental constraints and production requirements. Major economic problems may occur if the stripping and dumping dynamics are not optimally sequenced. In MSF mining operations, equipment selection and material schedules are constrained by multivariate random fields. These random fields are subject to future uncertainties, which might render an entire project uneconomic. Stochastic models are therefore required to completely define the underlying uncertainties. To develop the proposed economic models, comprehensive stochastic-optimization formulations provide a generic platform to simulate different scenarios. Adequate knowledge of the challenges of MSFs provides understanding into improving equipment productivity while different scenario simulations offer a means to evaluate different operating conditions.
Relevant literature
Dragline research initiatives have resulted in the development of excavation and spoiling dynamic models [4-6]. Economic models have also been developed to identify mining complexities and examine different excavation alternatives [7-9] studied dragline-bulldozer and cast blasting (CSB) techniques, respectively. The authors concluded that working bench advancement and the economic gains of ancillary operations require optimal schedules. NLP and Lagrange Multiplier Methods (LMM) have been applied to mine production schedules. Dagdelen and Johnson [10] applied Lagrangian parameterization algorithms to optimize production schedules in open pit mines. Pendharkar and Rodger [11] developed a generalized NLP model to eliminate excessive scheduling and inventory problems in coal industries. NLP models provides better profit margins compared to LP models, however, the concept is limited to very simple cases [11]. SOP minimizes future unexpected occurrences by taking into account all possible outcomes. In the long run, this process achieves a better decision than using only specific scenario(s) [12-14]. Shih and Frey [15] used a multi-objective chance-constrained optimization model to determine optimal coal blends. The limitations of the traditional LP and NLP approaches were mitigated by defining the intrinsic variability of coal properties. Despite these improvements, quantitative dragline production must be incorporated in optimization models. The intrinsic variability of excavation and spoiling dynamics in MSFs must also form part of existing models.
Multi-seam formation extraction
Multi-seam formations (MSFs) parameters can be divided into two. These include physical and economic parameters: The physical parameters are divided into
(i) Machine design
(ii) Mine production and layout
(iii) External factors
(iv)Geological variables
Dragline productivity is directly influenced by mine layouts, pit geometries and the selected excavation method. In varying geologic formations, the dragline reach and geometry require sufficient technical improvement to increase productivity. Draglines and ancillary operations tied up in a complex interactive domain could result in limiting economic factors. Also, material rehandling and dragline walking times are some of the major concerns in thick overburdens. In such situations, the main challenge is the increase in swing angles. Geologic uncertainties of MSFs and the stochastic nature of economic variables, result in difficulties during excavation schedules. Ultimate pit layouts and production schedules are highly sensitive to marginal changes in economic and operating variables [7]. The major challenge resulting from economic variables is the determination of quantitative relationships that incorporate the physical parameters of the deposit.
Coal quality parameters: The quality of the final coal products is controlled by chemical variables. These variables can occur randomly over the coal domain due to alteration zones and general morphological characteristics of the deposit. The large size and geometry of strip mine designs render selective mining unlikely. Thus, blending to achieve desired quality is mostly conceivable at the processing stage. Due to geologic uncertainties of MSFs, incorporating chemical and physical variables into the overall economic model require stochastic definitions. Heuristic methods are obviously very inefficient to meet these challenges.
NLP Model for Equipment Selection and Coal Seam Extraction in MSFs.
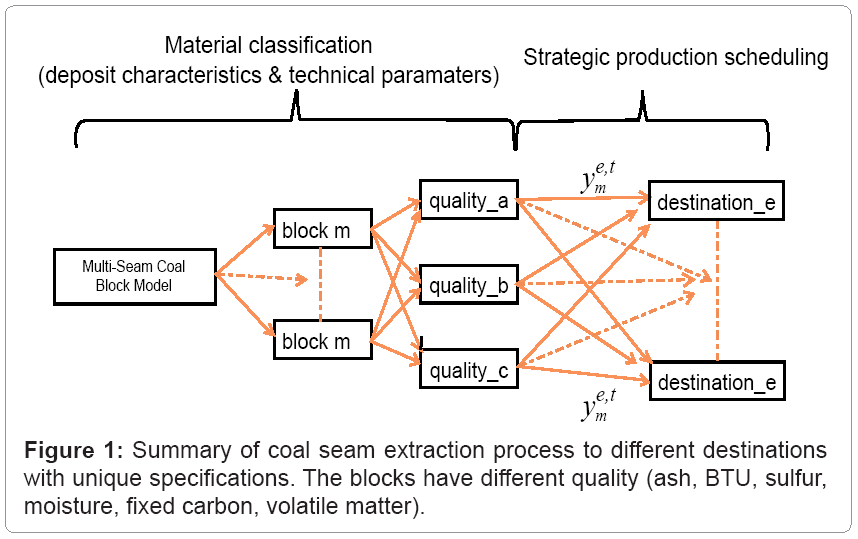
The objective function is to maximize the Net Present Value (NPV) generated from mining and processing each block. Mining cost is defined as a function of the resource j allocated to mine a ton of block n in periodk. The revenue is a function of the portion of seam-cut m extracted and transported to destination e in period t. The discounted profit is equal to the discounted revenue obtained by selling the final product in seam-cut m to destination e in period t minus the discounted cost of mining all the material in block n as waste in period k by resource j Equation (1) illustrates the overall objective function. All symbols, variables, and abbreviations used in the formulations are indicated in the Appendix.
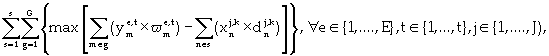 (1)
(1)
Equations (2) and (3) show the formulations for 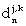 and
and 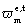 etm respectively.
etm respectively.
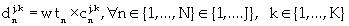 (2)
(2)
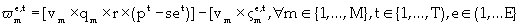 (3)
(3)
For computational purposes, the model is divided into two sections: (i) waste excavation and (ii) coal seam extraction. The NLP model is based on the generalized LMM [16].
Waste excavation model
The objective is to minimize mining cost. This includes resource (equipment) allocation for topsoil, overburden and inter-burden excavation. The cost function incorporates equipment productivity as well as the relative spatial locations of each mining strip. Equation (4) shows the objective function formulation.
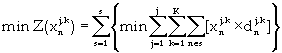 (4)
(4)
The constraint functions are formula as follows
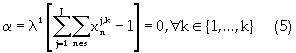
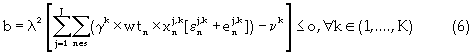
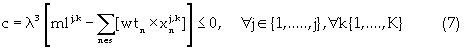
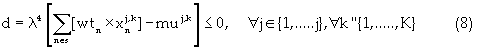

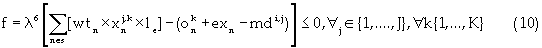
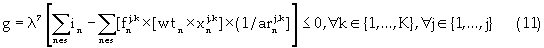
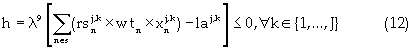
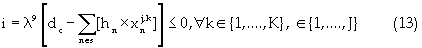
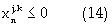
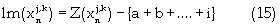
Equation (5) is the reserve constraint. Equation (6) is the energy constraint that regulates the energy consumption based on a minimum permissible total energy cost. Equations (7) and (8) are the mining capacity constraints, which limit the excavation by each resource within lower and upper bounds, respectively. Strip mining activity is such that internal dumping must be concurrent with block excavation. Hence, dump area availability limits the material excavated. Equation (9) controls the dumping mechanism based on the dump volume availability. The next constraint is the minimum mining width/resource interaction shown in equation (10). Equation (10) comprises the total length of the mining-strip, the external length of space outside the digging domain; and the minimum drop cut width for each resource. The next constraint shown in equation (11) defines equipment selection and scheduling based on the dig ability index. This constraint ensures efficient equipment-formation interaction. Equations (12), (13) and (14) are the labor, critical bench height, and non-negativity constraints respectively. The labor constraint matches the available skilled labor to each resource labor requirement for all periods. A critical digging depth constraint is defined beyond which dragline digging process is inefficient. This constraint is based on the fixed digging geometries of draglines. Equation (15) presents the Lagrangian model; hence instead of optimizing the function 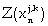 the Lagrange function
the Lagrange function 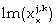 is rather optimized.
is rather optimized.
Coal seam extraction
The objective function is to maximize the revenue generated from the mining activity. The model incorporates variable geologic and economic parameters, contractual specifications and extraction dynamics. A summary of the entire optimization process is shown in figure 1 where coal products with different qualities are transported to specific destinations.
The objective function is formulated as shown in equation (16).
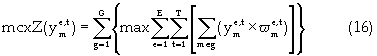
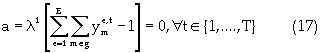
The coal seam extraction NLP model constraints are formulated as:
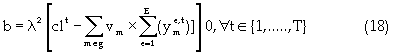
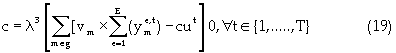
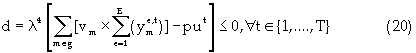
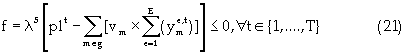
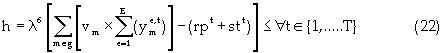


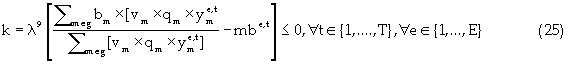
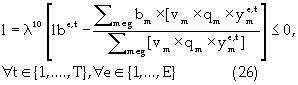

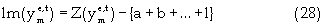
Equation (17) represents the reserve constraint. Equations (18) and (19) show the minimum and maximum mining capacity constraints respectively. The mining capacity is defined by the productivity of the extraction equipment, managerial specifications and the excavation geometry. Coal processing capacities are functions of the mine life, stripping geometry, processing facilities, economics, and mineable reserves. Equations (20) and (21) are respectively, the upper and lower limits on the processing capacity. Transportation and stockpile capacity constraint is represented by equation (22). This constraint is a function of the economics of the project and market conditions. Market condition is governed by contractual agreement and market absorption capacities. The maximum and minimum bounds are illustrated respectively by equations (23) and (24). Blending might be complicated by achieving a final product whose quality is outside the acceptable limits. To prevent these occurrences, minimum and maximum constraints are formulated for each quality-defining parameter. Equation (25) and (26) specify the upper and lower limits respectively. Non-negativity constraint is defined by equation (27). Equation (28) is the Lagrangian model.
Stochastic simulation and risk analysis
The stochastic variables associated with MSFs are identified and modeled using probability distribution functions (PDFs). The respective PDFs are obtained from detailed data analysis and model fitting. Simulation of the variable parameters is limited to Monte Carlo and Latin Hypercube techniques. The results lead to real-time-feed risk analysis for the economic model.
Numerical solution technique
The solution algorithm to the NLP model is the Generalized Reduced Gradient (GRG) Algorithm. The optimizer is initiated by evaluation of the Jacobian (JC) matrix of Partial Derivatives (PD) of the problem functions with respect to the decision variables [17]. The GRG algorithm is implemented in SOLVER [18]. @RISK [19] forms the platform for the stochastic modeling. Numerical values are assigned to risk profiles using empirical data and qualitative assessments.
Implementation of the Model to a Bituminous MSF
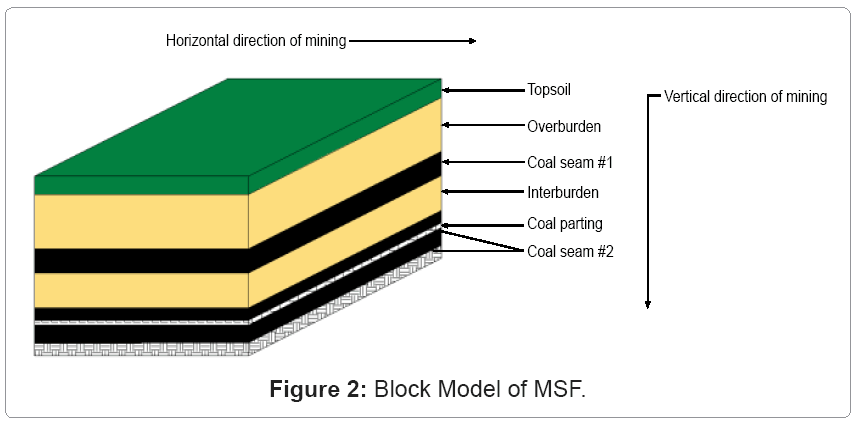
The Wise formation comprises a 2,070foot-thick mass of shale and at least nineteen coal seams lying between the Gladeville and Harlan sandstone [20]. This paper considered mining in two of the major seams (thereinafter referred to as seam #1 and seam #2) with dimensions shown in table 1. The basin had variable coal properties shown in table 2, and the mining area dimension was given as 4km by 2km. Figure 2 shows the geologic block model. Based on the given geologic rock properties and technical specifications, the following equipment and excavation options were investigated as possible extraction decisions
(i) Dragline
(ii) ripper-dozer
(iii) CSB
(iv) Shovel and Truck (SHT) system
| Description | Value |
|---|---|
| Topsoil thickness (ft) | 3 - 10 |
| Overburden thickness (ft) | 80 - 120 |
| Inter-burden thickness (ft) | 40 - 50 |
| Seam #1 thickness (ft) | 20 |
| Seam #2 thickness (ft) | 40 |
| Coal partings thickness in seam #2 (ft) | 4 |
Table 1: MSF Extent and Parameters
| Description | Value | |
|---|---|---|
| Seam #1 | Seam #2 | |
| Moisture (%) | 2.1 - 3.7 | 1.5 - 4.3 |
| Volatile matter (%) | 34.5 - 37.5 | 32.8 - 38.4 |
| Fixed carbon (%) | 51.3 - 54.7 | 55.4 - 61.6 |
| Ash (%) | 5.6 - 10.5 | 1.7 - 4.6 |
| Sulfur (%) | 0.7 - 1.1 | 0.4 - 0.8 |
| BTU | 12,790 - 13,910 | 13,720 - 14,810 |
Table 2: Coal Quality Parameters [20].
The capital (CAPEX) and operating cost (OPEX) estimates are shown as follows (x represents the maximum volume excavated per hour [21] (Table 3-5).
| Strip #1 | ||||||
|---|---|---|---|---|---|---|
| Dragline | Dozer | SHT | CSB | |||
| ε(J) | 12 | 2 | 7 | 15 | ||
| e(J) | 8 | 4 | 13 | 20 | ||
| Strip #2 | ||||||
| ε(J) | 12 | 2 | 7 | 15 | ||
| e(J) | 8 | 4 | 13 | 20 | ||
| Strip #3 | ||||||
| ε(J) | 12 | 2 | 7 | 15 | ||
| e(J) | 8 | 4 | 13 | 20 | ||
| Strip #4 | ||||||
| ε(J) | 12 | 2 | 7 | 15 | ||
| e(J) | 8 | 4 | 13 | 20 | ||
Table 3: Excavation and Dumping Energy Consumption Rates.
| Periods | ||||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Dragline | ||||
| Dump capacity (106ft3) | 220 | 219 | 134 | 94 |
| Dozer | ||||
| Dump capacity (106ft3) | 260 | 246 | 238 | 92 |
| SHT | ||||
| Dump capacity (106ft3) | 310 | 310 | 310 | 310 |
| CSB | ||||
| Dump capacity (106ft3) | 310 | 310 | 288 | 246 |
Table 4: Periodic Dump Volume Availability.
| Destination | Seam #1 | Seam #2 |
|---|---|---|
| 1 | 20.19 | 20.92 |
| 2 | 19.64 | 20.35 |
| 3 | 20.19 | 20.92 |
| 4 | 17.98 | 18.62 |
| STK | 25.15 | 26.08 |
Table 5: Mining and Coal Transportation Costs (US$).
Dragline
P&H 9010C dragline model with 75yd3 bucket capacity was considered. The CAPEX was estimated at US$80 million per unit. The OPEX consisted of 67% parts and 33% fuel and lubrication (equipment), and 78% operator labor and 22% repair labor (labor). Equation (29) is the OPEX estimates in US$/yd3.
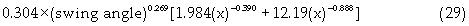
Dozer
CAT D11 of blade capacity 57yd3 was considered. The CAPEX was estimated at US$2 million per unit. The OPEX estimates were based on excavation and material relocation; distributed as: 47% parts and 53% fuel and lubrication (equipment), and 86% operator labor and 14% repair labor (labor). Equation (30) is the OPEX estimates in US$/yd3.
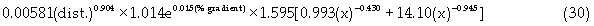
SHT
CAT 7495HD cable shovel with 40-80yd3 bucket capacity was selected. The CAPEX was estimated at US$35 million per unit. CAT 793F truck with nominal payload capacity of 249.45 tons was also selected with an estimated CAPEX of US$3 million per unit. The SHT system was treated as one entity hence, the OPEX (US$/yd3) for this system was given by equation (31).
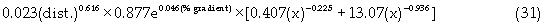
CSB
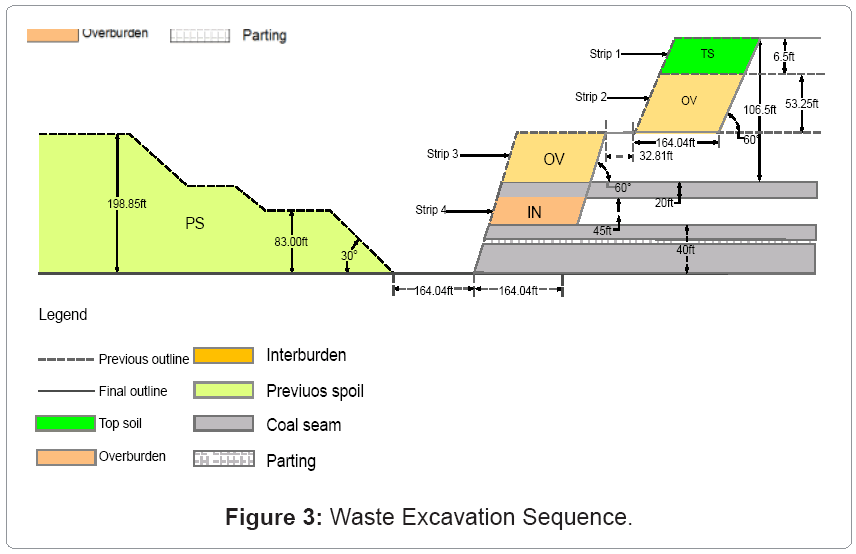
CSB reduces the time required by dragline to swing and cast material by 25 to 30% Ray et al. (2009). It was therefore assumed that the overall stripping cost is approximately 12.1% less the stripping cost of draglines. The CAPEX was also assumed to be US$2 million. Figure 3 (Table 6,7) shows the predefined mining directions and schedule. The material specific gravities were given as 1.08tons/yd3, 0.54 tons/yd3 and 2.16 tons/yd3 respectively for coal, topsoil and overburden/inter-burden material. The productivities were calculated as: 4617yd3/hr, 190yd3/hr, 4808.48yd3/hr and 13,851yd3/hr for the dragline, dozer, SHT, and CSB respectively. The availability of internal and external dumps was assumed to be decreased by the volume of the previous cuts. Mechanical availability was given as 90% of the 20hrs/day per 300day/yr for all equipment. The minimum mining width/resource interaction constraint was also neglected for the dozer and CSB options due to their extraction mechanisms. Four destinations were considered in the supply chain of the bituminous coal. On-site stockpiles were also defined to account for material mined and processed beyond the demand limits. Ten percent discount rate for all prices and costs was assumed. US$ 41.01 per ton coal price and US$5. 42 per ton selling price were considered. The maximum processing capacity was calculated as 880tons/hr (minimum capacity was given as 32% of maximum capacity). The stripping ratio was calculated as 4.89 (tons: tons). The economic analysis and parameters were limited within the US economy. All other input data for the model are provided in the Appendix.
| Destination | Seam #1 | Seam #2 | ||
|---|---|---|---|---|
| min | max | min | max | |
| 1 | 409.5 | 630 | 266.18 | 630 |
| 2 | 330.9 | 509 | 215.05 | 509 |
| 3 | 318.5 | 490 | 207.03 | 490 |
| 4 | 377.65 | 581 | 245.47 | 581 |
| STK | 0 | 1260 | 0 | 1260 |
Table 6: Contractual Coal Quantity Limits (103 tons).
| Destination | Calorific value | Sulfur | Fixed carbon | Ash | Moisture | Volatile | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (103btu/Ib) | (%) | (%) | (%) | (%) | (%) | |||||||
| Seam #1 | ||||||||||||
| min | max | min | max | min | max | min | max | min | max | min | max | |
| 1 | 10 | 15 | 0.2 | 1 | 50.20 | 65.30 | 0.50 | 15.60 | 1.25 | 5.20 | 12.50 | 40.90 |
| 2 | 10.5 | 14.8 | 0.15 | 1.22 | 48.50 | 67.00 | 1.90 | 13.80 | 2.80 | 4.80 | 18.10 | 50.20 |
| 3 | 9.5 | 15.5 | 0.36 | 0.98 | 49.00 | 63.20 | 3.60 | 16.00 | 2.75 | 5.10 | 20.00 | 45.00 |
| 4 | 12.5 | 14.9 | 0.4 | 1 | 45.00 | 70.00 | 4.80 | 14.90 | 1.90 | 5.00 | 18.00 | 37.20 |
| STk | 0 | 14.8 | 0 | 1.1 | - | 54.70 | - | 10.50 | - | 3.70 | - | 37.50 |
| Seam #2 | ||||||||||||
| 1 | 10 | 15 | 0.13 | 0.83 | 50.20 | 65.30 | 0.21 | 18.00 | 1.30 | 5.20 | 8.20 | 50.20 |
| 2 | 10.5 | 14.8 | 0.6 | 0.9 | 48.50 | 67.00 | 0.70 | 16.70 | 2.00 | 4.80 | 10.60 | 51.10 |
| 3 | 9.5 | 15.5 | 0.4 | 0.88 | 49.00 | 63.20 | 2.90 | 18.00 | 2.00 | 5.10 | 12.00 | 48.50 |
| 4 | 12.5 | 14.9 | 0.2 | 0.84 | 45.00 | 70.00 | 2.15 | 18.00 | 1.89 | 5.00 | 18.00 | 37.20 |
| STk | 0 | 14.81 | 0 | 0.8 | - | 61.60 | - | 4.60 | 2.50 | 4.30 | 32.80 | 38.40 |
Table 7: Contractual Coal Quality Limits.
Results and Discussions
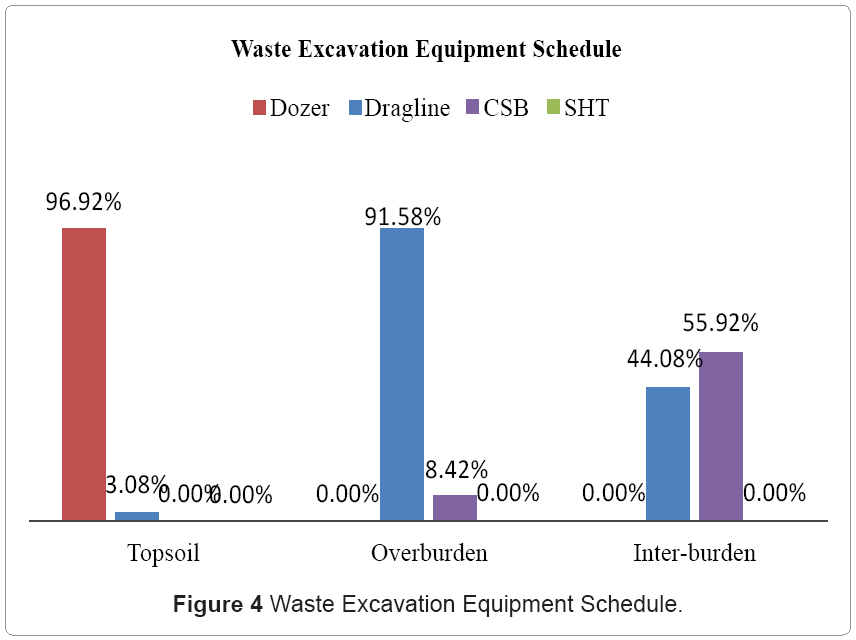
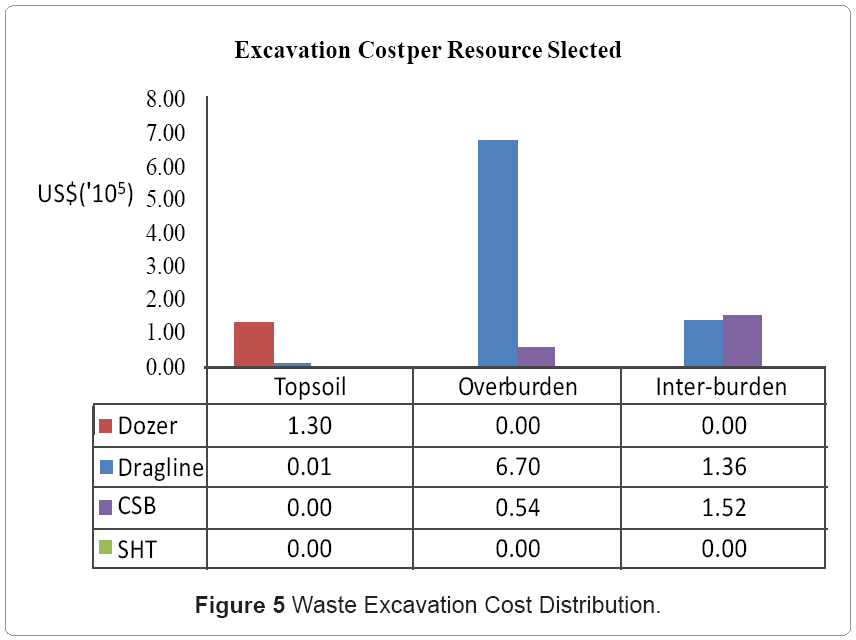
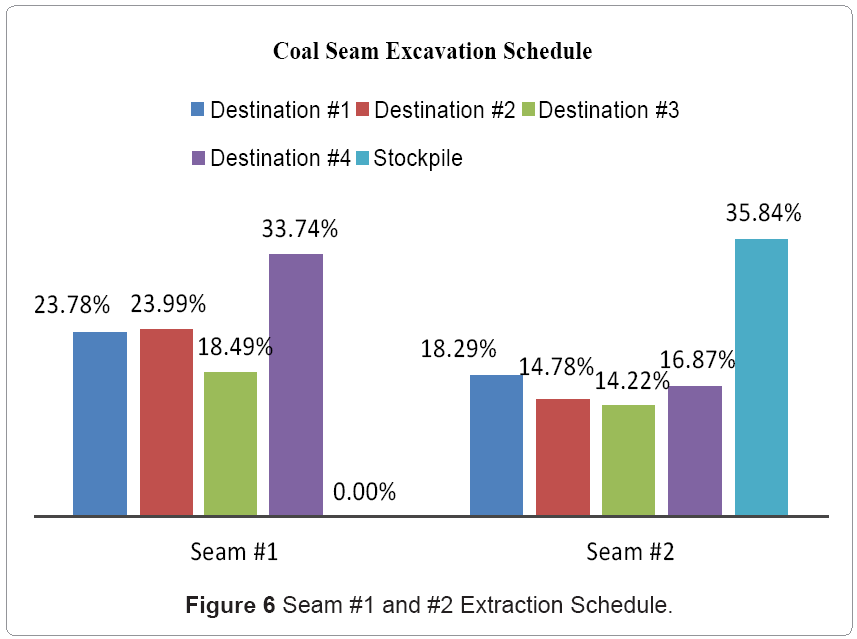
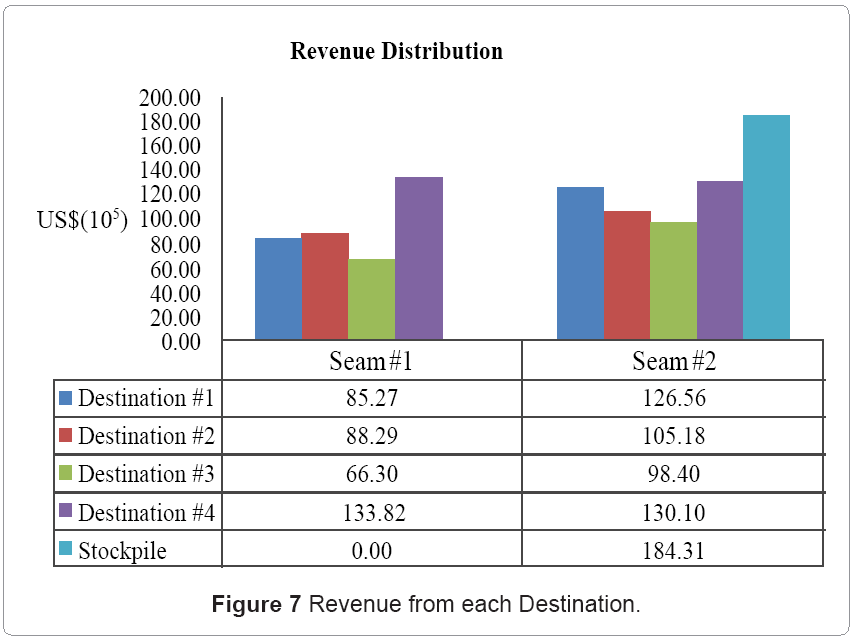
Given that the coal seam extraction was concurrent with waste excavation, the results showed a minimized mining cost of US$ 1.14 million for the 4 strips (see Figure 3) and approximately US$ 149.34 million for the entire deposit; a 3.51% decrement compared to the conventional traditional methods (dozer pushes topsoil and dragline excavates overburden/inter-burden). The dozer was scheduled to excavate 96.92% of topsoil (strip-1) in period 1; influenced by the material properties and specified material relocation mechanisms. The dragline was allocated to 3.08% of topsoil (strip-1) in period 1, 95.21% of overburden (strip-2) in period 2, 87.94% of overburden (strip-3) in period 3, and 44.08% of inter-burden (strip-4) in period 4. The SHT system was not scheduled in any of the periods due to their relatively high OPEX cost and energy requirements. The CSB technique was allocated to 4.79% of overburden (strip-2) in period 2, 12.06% of overburden (strip-3) in period 3, and 55.92% of inter-burden (strip-4) in period 4 (as a result of the digging constraint on the dragline). Figure 4 in the Appendix illustrates the results of the waste excavation model. The optimal revenue obtained was US$ 61.56 million for the first two strips by transporting 23.78% and 18.30% of seam #1 and #2 respectively to destination 1; 23.99% and 14.78% respectively of seam #1 and #2 to destination 2; 18.49% and 14.23% respectively of seam #1 and #2 to destination 3; 33.74% and 16.87% respectively of seam #1 and #2 to destination 4. The optimal solution also stockpiled excavated portions of seam #2 (35.84%) due to the maximum capacity limits of the destinations Figure 5. Seam #1 was however, fully mined and transported to all destinations (see Figure 6 in the Appendix). The net present value was calculated as US$ 31.69 million for the first 20yrs; a 0.19% increment compared to the conventional traditional schedule (dozer pushes topsoil and dragline excavates overburden/inter-burden). This percentage will increase further considering draglines operating in inefficient conditions (violation of critical bench height and material rehandling constraints), and sub-optimal blending ratios.
Risk simulation modeling and analysis
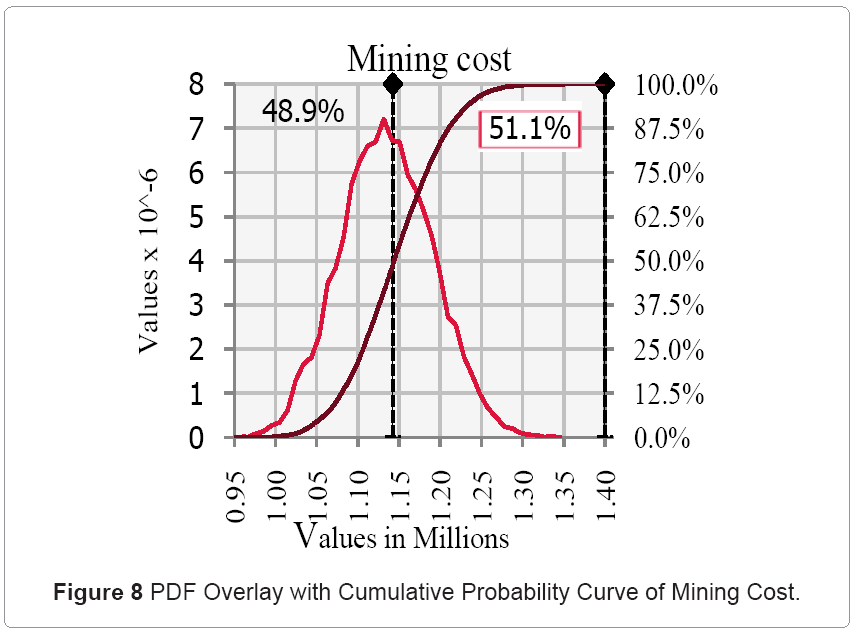
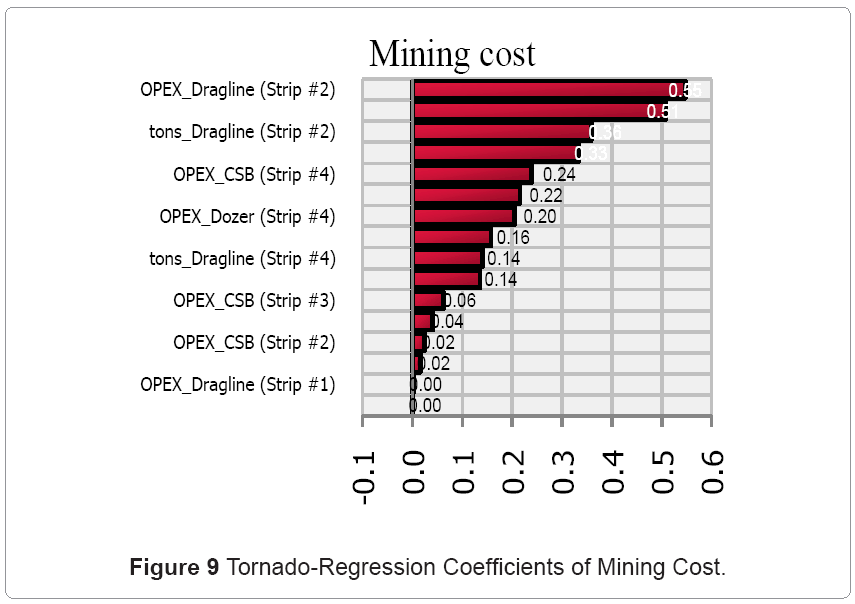
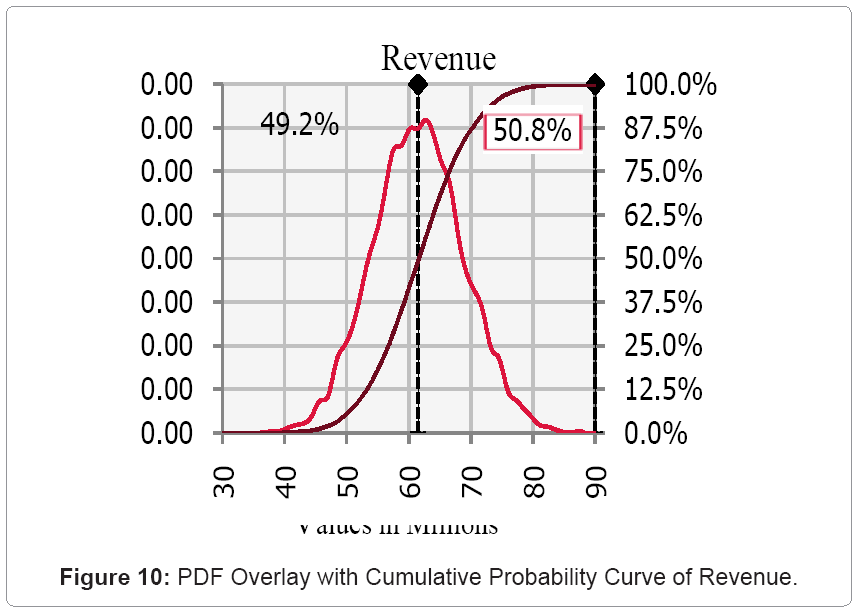
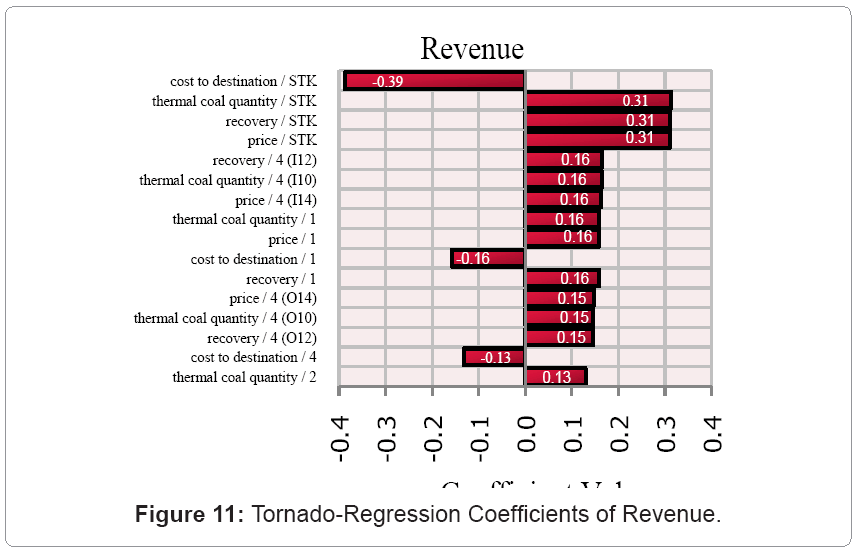
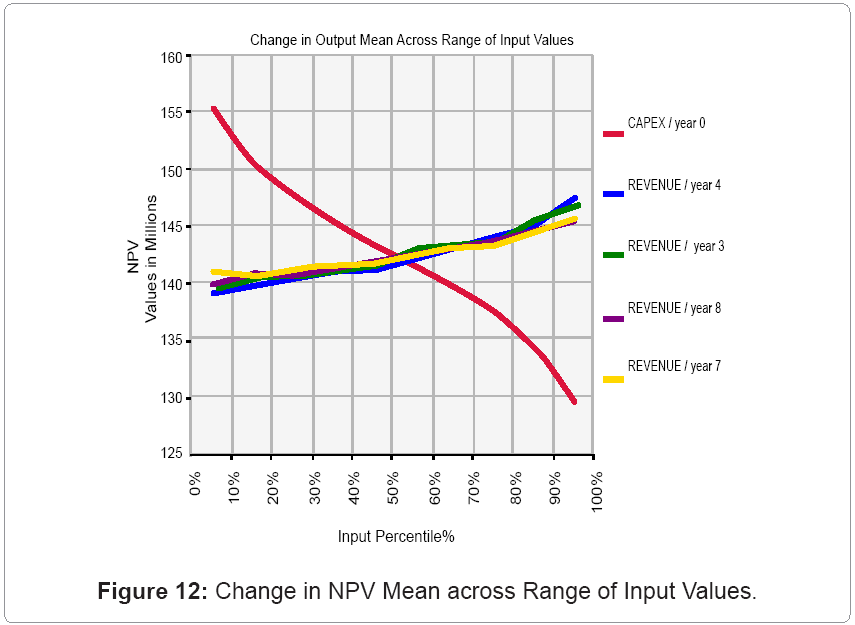
The objective is to determine the effect of multiple uncertainties on the stochastic input parameters (geologic variability, economic uncertainties and excavation/spoiling dynamics). This process identified, evaluated and estimated the level of risks involved in the waste excavation and coal seam extraction models; their comparison against specified benchmarks; and the determination of acceptable risk margins. The risk analysis was done in @RISK [19] with 10,000 iterations in 10 simulation runs. The optimal simulation parameters were obtained from experimental designs, where parameters were varied gradually to obtain distributions for the mean values and variances of reach run. The results were graphed to determine zones of parametric stability. Best Fit [19] was used to fit probability distributions to the available data. Normal PDFs were applied to mining, processing, and capital costs with ±20% (values determined from qualitative and quantitative data analysis). Lognormal PDF was applied to commodity price with the same truncations as discussed above. Uniform PDFs were used to model the processing recoveries, thermal coal quantities, and the total tons of material. The selling price was modeled with the triangular PDF with ±20% truncations. The results indicated a 51.1% chance of the OPEX figures increasing above its current values and a 49.2% probability of the revenue falling below the current estimates. The dragline OPEX and the excavated-tons schedule were the major risk parameters (0.55 regression coefficient) while the OPEX of CSB technique was the least (0.02 regression coefficient) of the mining cost. Tornado analysis showed the cost of stockpiling material in all periods as the greatest risk parameter (-0.39regression coefficient) while the cost to the 4th destination was the least (-0.13 regression coefficient). The Weibull distribution described the dragline OPEX and the excavated-ton risk profiles while the Normal distribution best fitted the mining cost and the revenue risk profiles. Refer to (Figure 7-12) in the Appendix for all the resulting graphs.
Conclusions and Future Works
The proposed models were able to improve dragline productivity in complex MSF excavation domains by characterizing the various stochastic input parameters. The user-written mathematical formulations offered the flexibility of constraining excavation and spoiling dynamics within technical, operations and economic specifications of the mine. The model again offers the planner a robust platform to simulate different scenarios with regards to dragline operating dynamics and ancillary equipment allocation. The optimal solutions are subjected to risk simulation and modeling to determine the economic impacts of the stochastic variables. The SOP models improved the overall NPV and mining cost, respectively, by +0.19% and -3.51% compared to the conventional traditional schedule (dozer pushes topsoil and dragline excavates overburden/inter-burden). The optimal waste excavation equipment schedules for all periods include
(i) Topsoil (96.92% by dozer and 3.08% by dragline)
(ii) Over burden (91.58% by dragline and 8.42% by CSB technique)
(iii) Inter-burden (44.08% by dragline and 55.92% by CSB technique)
The optimal coal seam extraction schedule for all periods include: (i) seam #1 (23.78% to destination #1, 23.99% to destination #2, 18.49% to destination #3, 33.74% to destination #4) and (ii) seam #2 (18.30% to destination #1, 14.78% to destination #2, 14.23% to destination #3, 16.87% to destination #4, and 35.84% stockpiled). The concept involved is generally applicable and should not be limited to this case only. Future research will focus on coupling the stochastic analysis with the optimizer through a visual basic programming language. This will enable the development of a comprehensive model with graphical user interface. Some functions in the optimization model exhibit discontinuity; an area which will be investigated in future research for a more robust SOP model.
References
- Demirel N, Frimpong S (2009) Dragline dynamic modelling for efficient excavation. Int J Min Reclam Environ 23: 4-20.
- Paraszczak J, Fytas K (2012) Renewable energy source- a promising opportunity for remote mine sites. Int Confer on Renewa Energy and Power Quality (ICREPQ’12), Santiago de Compostela, Spain.
- Erdem B, Düzgün HSB (2005) Dragline cycle time analysis. J Sci Ind Res 64: 19-29.
- Tanaino AS (1986) Automation of quarry planning. Mining-Geometry Calculations, Nauka, Moscow.
- Vasilyev YI, Zaitseva AA, Cheskidov VI (1999) Mining regime stabilization in working inclined deposits by blocks. J Min Sci 35: 633-639.
- Zaitseva AA, Cheskidov VI, Zaitsev GD (2007) Effect of the mining sequence on the internal dump capacity in an open pit. J Min Sci 43: 508-515
- Falkie VA, Porter EW (1973) Economic surface mining of multiple seams. Proceedings of application of computer methods in the mineral industry.
- Ray SK, Zutshi A, Sarkar M (1999) Cast blasting-state of the art. Fragblast 3: 291-302.
- ZHOU W, CAI QX, CHEN SZ (2007) Study on dragline-bulldozer operation with variations in coal seam thickness. Journal of China University of Mining and Technology 17: 464-466.
- Dagdelen K, Johnson TB (1986) Optimum open pit mine production scheduling by Lagrangian parameterization. Proc. of the 19th International Symposium on the Application of Computers and Operations Research in the Mineral Industry, Littleton, 127-142.
- Pendharkar PC, Rodger JA (2000) Nonlinear programming and genetic search application for production scheduling in coal mines. Annals of Operations Research 95: 251-267.
- Winston WL (1996) Simulation modeling using @RISK, School of Business Indiana University.
- Leite A, Dimitrakopoulos R (2007) Stochastic optimisation model for open pit mine planning: application and risk analysis at copper deposit. Mining Technology 116: 109-118.
- Richmond A (2011) Evaluating capital investment timing with stochastic modeling of time-dependent variables in open pit optimization. J Min Sci 47: 227.
- Shih JS, Frey HC (1995) Coal blending optimization under uncertainty. European Journal of Operational Research, 83: 452-465.
- Everett H (1963) Generalized Lagrange multiplier method for solving problems of optimum allocation of resources. Operations research 11: 399-417.
- Fylstra D, Lasdon L, Watson J, Waren A (1998) Design and use of the Microsoft Excel Solver. Interfaces 28: 29-55.
- Frontline Systems (2013) Excel Solver, ©Frontline Systems Inc., Nevada, USA.
- Palisade (2012) @RISK: Risk simulation and analysis for spreadsheet, Palisade Corporation, Newfield, New-York, USA.
- Henderson JA (1979) Summary of coal resources in Virginia. Division of Mineral Resources, Commonwealth of Virginia: Department of Conservation and Economic Development, Richmond, Virginia, USA.
- Bradley PC (2002) Supplemental teaching resources. US Bureau of Mines CES Capital Costs.
Relevant Topics
- Additive Manufacturing
- Coal Mining
- Colloid Chemistry
- Composite Materials Fabrication
- Compressive Strength
- Extractive Metallurgy
- Fracture Toughness
- Geological Materials
- Hydrometallurgy
- Industrial Engineering
- Materials Chemistry
- Materials Processing and Manufacturing
- Metal Casting Technology
- Metallic Materials
- Metallurgical Engineering
- Metallurgy
- Mineral Processing
- Nanomaterial
- Resource Extraction
- Rock Mechanics
- Surface Mining
Recommended Journals
Article Tools
Article Usage
- Total views: 16149
- [From(publication date):
specialissue-2013 - Aug 19, 2025] - Breakdown by view type
- HTML page views : 11464
- PDF downloads : 4685