The model of superfluid physical vacuum as a basis for explanation of efficacy of highly diluted homeopathic remedies

Liudmila B Boldyreva; Elena M. Boldyreva

doi:10.4172/2167-1206.1000109

ISSN: 2573-4555

Journal of Traditional Medicine & Clinical Naturopathy

Make the best use of Scientific Research and information from our 700+ peer reviewed, Open Access Journals that operates with the help of 50,000+ Editorial Board Members and esteemed reviewers and 1000+ Scientific associations in Medical, Clinical, Pharmaceutical, Engineering, Technology and Management Fields.

Meet Inspiring Speakers and Experts at our 3000+ Global Conferenceseries Events with over 600+ Conferences, 1200+ Symposiums and 1200+ Workshops on Medical, Pharma, Engineering, Science, Technology and Business

The model of superfluid physical vacuum as a basis for explanation of efficacy of highly diluted homeopathic remedies

*Liudmila B. Boldyreva^1 and Elena M. Boldyreva²**
¹The State University of Management, Moscow, Russia
²Peoples’ Friendship University of Russia, Moscow, Russia
Corresponding Author :	Liudmila B. Boldyreva The State University of Management Moscow, Russia Tel: +7910-413-1776 E-mail: boldyrev-m@yandex.ru
Received December 20, 2011; Accepted April 16, 2012; Published April 18, 2012
Citation: Boldyreva LB, Boldyreva EM (2012) The Model of Superfluid Physical Vacuum as a Basis for Explanation of Efficacy of Highly Diluted Homeopathic Remedies. J Homeop Ayurv Med 1:109. doi: 10.4172/2167-1206.1000109
Copyright: © 2012 Boldyreva LB, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.

Visit for more related articles at Journal of Traditional Medicine & Clinical Naturopathy

View PDF Download PDF Tables & Figures

Keywords

Homeopathy; Veterinary; Ultra-low doses; Model of superfluid physical vacuum; Spin structures in physical vacuum; Spin supercurrents

Introduction

The homeopathic remedies used nowadays represent dilutions of D30 and higher. Note that the probability of the event that a D30 dilution of 1 mole of a substance contains at least one molecule will be ~0.001%. This makes explanation of the efficacy of highly diluted homeopathic remedies extremely difficult in the framework of existing physical conceptions.

That is why along with attempts to explain the effects of highly diluted remedies on organisms from the physical standpoint, there are explanations based on the placebo effect. The latter is associated with a therapeutic effect caused by suggestion or autosuggestion inducing a positive response of the immune system.

However, the efficacy of using highly diluted homeopathic remedies for treating animals, including evidence given in this paper, cannot be accounted for by the placebo effect, which applies to humans only.

It is noteworthy that the positive results of homeopathic treatment of animals, i.e. cows, as described in this paper, are often achieved by using the same homeopathic medicines that are used in treating similar diseases in humans. Thus both for humans and for animals there seem to be the same mechanism of “correcting” the organism’s functions (No doubt, the placebo effect may take place as concerns humans, however, there should be a different mechanism determining the efficacy of treating an organism with a highly diluted homeopathic remedy).

Looking at the problem from the physical standpoint, it is natural to use the formalism of quantum physics. Firstly, in quantum physics the size of a particle is determined by its de Broglie wavelength. The de Broglie wavelength of a quantum object can exceed the classical size of the quantum object by some orders of magnitude (e.g. the de Broglie wavelength of the electron in a hydrogen atom in the ground state is five orders of magnitude greater than the electron’s “classical” radius). As a result of this, the notion of substance concentration ceases to have its conventional meaning in this case. Secondly, there are effects, relating to quantum nonlocality, which suggest that quantum correlations may exist between any quantum objects, including correlations between the remedy and target organism as consisting of quantum objects.

There are a number of works where the explanation of some effects of homeopathic remedies is based on concepts of patient-practitionerremedy entanglement, [1-3]. But to the authors’ knowledge, no physical process in physical vacuum has been proposed so far for explanation of the effects of highly diluted homeopathic remedies.

Note that the effects of highly diluted homeopathic remedies on organisms are similar to those of low-intensity electromagnetic radiation and low-density streams of quantum particles (electron, proton, neutron, etc.) [4,5]. This suggests that there is the same physical mechanism underlying the effects of ultra-low doses on biological systems.

It is shown in this paper that under assumption that physical vacuum has the properties of superfluid ³Ðï¿½Ðµ-Ðï¿½ [6-8] the effects of ultralow doses (ULD) of biologically active substances (BAS) on biological objects (BO) can be taken to be due to spin supercurrents between spin structures produced in such physical vacuum (hereinafter referred to as the superfluid physical vacuum âï¿½ï¿½ SPV) by the BAS and the target BO [8-10]. The properties of these spin supercurrents are similar to those of spin supercurrents in superfluid ³He-B.

Thus the main feature of the approach discussed here is that it is based on accounting for the properties of physical vacuum.

Treatment of Cows Using Homeopathic Remedies

Experiments described below were initiated in Russia in 1999, a period of a considerable fall in agricultural production, caused by economic situation in the country; they had been conducted before the implementation of the government-supported National Project of development of agriculture.

The experiments were carried out on two large farms of the Moscow region. Out of date equipment (e.g. dairy machines), wearout of ventilation systems, wear-out of the barn premises led to a high incidence of various diseases of the cows and calves. In these “extreme” conditions homeopathic remedies were used in the therapy of the milking cows with mastitis [11].

A great advantage of the use of homeopathic remedies over the administration of antibiotics in the case of mastitis is that after the treatment milk can be used without any restrictions. In the research conducted, conventional and homeopathic methods of treating cows with serous and catarrhal mastitis were studied. Mastitis was caused mainly by improper milking machine functioning and had traumatic etiology. In summer period cows were also fetched to pasture that increased the incidence of traumatic mastitis. There was a loss in milk production; milk had a watery appearance and flakes in it. Udder quarters affected were reddened, edematous, painful and hot to the touch. California Mastitis Test was conducted additionally to estimate somatic cell count that proved to be elevated.

Two experiments were conducted at an interval of six months, that is, with different weather conditions. In the 1^st experiment 44 lactating cows with mastitis were equally allocated to the control and the experimental groups; in the second experiment 32 cows with mastitis were divided into two equal groups, the control and the experimental ones. At the beginning of both experiments the cows of both the control and experimental groups had the same symptoms of mastitis described above.

table 1 shows the schedule of administering antibacterial medications to the cows of the control group in both experiments, and homeopathic remedies to the cows of experimental group in the 1^st experiment, and those of experimental group in the 2^nd experiment.

The homeopathic remedies used were as follows, Traumeel ad us. vet. and Echinacea compositum ad us. vet. which are complex homeopathic remedies, namely produced by Biologische Heilmittel Heel GmbH, Germany (www.heel.de). Traumeel ad us. vet. contains fifteen plant, mineral and metallic ingredients in homeopathic dilutions from D3 to D11 [12]. Its “symptom picture” includes pain, inflammation, swelling and fever; this remedy is widely used in veterinary and human medicine in trauma-related conditions. It explains the choice of this remedy for the treatment of cows with mastitis, taking into account such dominant predisposing factor as trauma.

Echinacea compositum ad us.vet. contains eight ingredients of plant and animal origin, minerals and metals in homeopathic dilutions from D3 to D10 [13]. Its “symptom picture” is associated with inflammation, fever, swelling, reddening; this remedy is prescribed for stimulation of defense mechanisms of the organism.

A cow was considered to be cured clinically if the symptoms resolved completely (udder not swollen or painful, not hot), milk had normal organoleptic properties (normal color and consistency), and California Mastitis Test did not reveal high level of somatic cells.

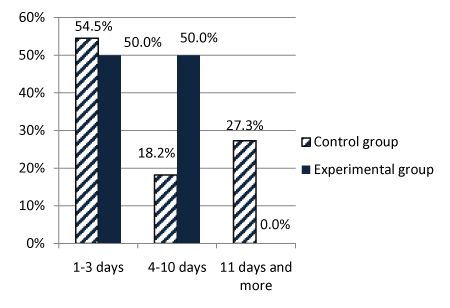
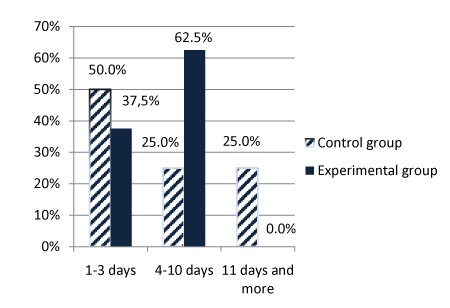
The percentage of animals cured in the 1^st experiment in various time intervals in days (the day number is counted off from the beginning of the experiment) is shown in Figure 1. A similar characteristic for the 2^nd experiment is shown in Figure 2. An average duration of mastitis in the experimental groups of the 1^st and the 2^nd experiment was 2.4 and 1.9 days less than that in the control ones correspondingly. In the control groups of the 1^st and 2^nd experiments 27.3% and 25% of cows recovered only after the 10^th day (up to 3 weeks) respectively, while in both experimental groups all the animals were cured by the 10^th day. A peculiarity of Echinacea compositum ad us.vet. is that in many cases at the beginning of its use a temporary exacerbation of the symptoms is noticed (1-2 days), but after that a quick recovery takes place. This is likely to be able to explain the lower percentage of recovered animals of the experimental group in the 2^nd experiment in the first three days of treatment in comparison with that in the 1^st experiment. The different percentages may also be associated with that the experiments were conducted in different seasons.

Note: At the same period of time, a series of experiments on homeopathic treatment of calves with gastrointestinal disorders (diarrhea) was conducted [14]. In the experiments, treatment of 94 calves at the age of 0-21 days was conducted. The calves were allocated to two equal groups: control and experimental. At the beginning of the experiment the calves of the control and the experimental groups had the same symptoms of diarrhea: very loose feces, severe dehydration of the organism, loss of appetite, depression, loss of skin elasticity, coat dullness, anemic mucous membranes, sinking of the eye within the orbit. Antibacterial medications, namely, Trimerazin per os and Bicillinum intramuscular were used in the control group. In the experimental group, complex homeopathic remedies namely, Mucosa compositum ad us. vet. and Berberis-Homaccord ad us. Vet. produced by Biologische Heilmittel Heel GmbH, Germany (www.heel.de), were administered subcutaneously every day.

Mucosa compositum ad us. Vet. is a unique remedy that is composed of extracts of mucous membranes derived from different organs of pig. All the extracts have dilution of D8. It also contains plant, mineral and metallic ingredients in dilutions from D4 to D28. This remedy is used in human and veterinary medicine for those patients who suffer from the inflammation of mucous membrane of various organs, including intestine [15]. Berberis-Homaccord ad us. vet. is a combination of three plant ingredients having 4 dilutions each, from D4 to D200 [16].

As a result, in the experimental group the recovery from diarrhea took 2.8 days, without use of antibiotics; in the control group the recovery from diarrhea took 5.0 days. The calves were considered to be cured clinically if the symptoms of diarrhea resolved completely.

The Model of Superfluid Physical Vacuum: A Brief Description

According to the model, physical vacuum has the properties of a superfluid and consists of pairs of oppositely charged particles possessing spins. In the unperturbed state the total spin of a pair equals zero. The model is based on the properties of superfluid ³Ðï¿½Ðµâï¿½ï¿½Ðï¿½, whose atoms have non-zero spin as well and form pairs whose total angular momentum (the sum of the orbital and spin angular momenta) is zero in the pure state. One of the properties of superfluid ³Ðï¿½Ðµ–Ðï¿½ is that areas with coherently precessing spins of ³Ðï¿½Ðµ atoms, the so-called homogeneously precessing domains (HPDs) [17-21], may exist there.

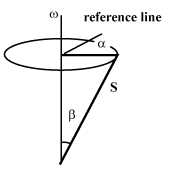
A HPD is characterized by spin S, precession angle (or precession phase) α, nutation angle β, and precession frequency ω (Figure 3). In a homogeneously precessing domain, energy U is related to the frequency ω of precession as

U = Sω (1)

According to the model, a quantum object is a HPD in the SPV [8].

The precession and nutation angles are angles of orientation of the order parameter, and there are processes that tend to make respectively equal both the values of precession angles and the values of nutation angles throughout the liquid volume. Such processes in superfluid ³Ðï¿½Ðµâï¿½ï¿½Ðï¿½ are spin supercurrents. For example, the value of spin supercurrent in the direction of axis z, J_z, is determined as follows:

(2)

Where, b₁ and b₂ are proportionality factors depending on β and the properties of the medium.

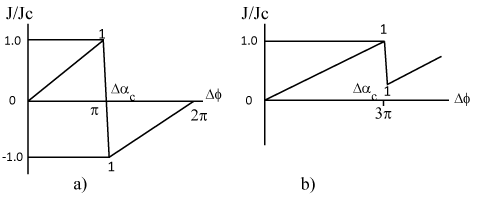
There exists such a phenomenon in ³Ðï¿½Ðµ–Ðï¿½ as phase slippage. At a certain difference in precession angles, &Delta;&alpha;_c, for two HPDs there takes place a precession phase slippage, or phase drop, by 2πn (n = 1, 2…). The critical spin supercurrent J_c corresponds to Δα_c [21]. Figure 4a and 4b show examples of the character of dependence of normalized spin supercurrent J/J_c between two HPDs with respective precession frequencies ω₁ and ω₂ (ω₁↑↑ω₂) on the hypothetical difference in the precession angles, Δφ which is defined as Δφ = (ω₁-ω₂)t, t being time. Up to the value of Δφ equal to Δα_c, the hypothetical difference is equal to the precession angles difference determining the spin supercurrent, Δα that is, Δφ = Δα. On the curves, the line 1–1 corresponds to the change in the supercurrent in the process of phase slippage, the 2π phase slip taking place. In Figure 4a, we have Δα_c = π [14]. In Figure 4b, Δα_c ≈ 3π [16].

Generally, the determination of time dependency of the magnitude of the spin supercurrent between two regions with precessing spins (for example, homogeneously precessing domains – HPDs, see Figure 3) is a difficult problem, because the speed of transmission of information of the existence of a gradient of the order parameter is, in theory, infinite, and the speed of the spin supercurrent is finite [21]. Besides, a possibility of phase slippage should be taken into account. The respective precession and nutation angles of interacting HPDs will become equal, provided the distance X between them and the difference between their precession frequencies, Δω, satisfy the following conditions:

Δω → 0 (3)

X → 0. (4)

The Mechanism of Action of Biologically Active Substances in Ultra-Low Doses on Biological Objects

According to the SPV model, a quantum object is a homogeneously precessing domain in physical vacuum, i.e. it is a spin structure in physical vacuum. The biologically active substance and the target biological object consist of quantum entities: electrons, protons, etc. Therefore, the biologically active substance and the biological object produce spin structures in physical vacuum.

We shall assume that the spin structure produced in the SPV by a BO is characterized by a single value of the precession frequency and single values of the angles of precession and nutation, that is, the structure is a homogeneously precessing domain in the SPV.

In the model discussed here, it is convenient to express ULDs of BAS in terms of so-called quanta. A “quantum” is such a dose of substance which produces in the SPV a spin structure that is characterized by single values of the precession frequency, the angle of precession and angle of nutation, and thus the structure can be thought of as being, like that of the BO, a HPD in the SPV.

To describe the spin structures produced in the SPV by a “quantum” of ULD of BAS and by that of a BO, we shall introduce a number of notions relating to time t: ω_1t will be the frequency of precession in the spin structure produced by the ULD of BAS, ω_2t the frequency of precession in the spin structure produced by the BO, and Δα_t the difference in the precession angles of the structures. Let us assume that the interaction of the ULD of BAS and the biological object starts at time t = τ₁. The difference in the precession angles, Δα τ₁, at time τ₁ is determined as

(5)

Where Δα₀ is the difference in the angles of precession of spin structures at time t = 0. In the special case of Δα₀ = 0 the equation (5) takes the form:

(6)

Note. There is lack of experimental data available on the character of dependence of spin supercurrents on the difference in the nutation angles of spin structures. Therefore, the nutation angles are not considered in the analysis of interaction between an ULD of BAS and a BO.

If the difference Δω = ω₁ τ₁ - ω₂ τ₁ meets the condition (3) (condition (4) is taken to be always met), then according to the properties of spin supercurrents there will be equalization of the precession angles. As follows from equations (5) and (6), the precession angles equalization results in a decrease in the difference in the precession frequencies in the spin structures produced by the ULD of BAS and the BO in the SPV, that is, for time τ₂ > τ₁ (provided that ω_1t does not change within the time τ₂- τ₁, and equals ω₁ τ₁) we can write:

Δα τ₂ ≈ 0,

(7)

Where variables Δα τ₂, ω₂ τ₂ correspond to respective Δα τ₁, ω₂ τ₁, but their values are taken at t = τ₂.

Thus the action of the ULD on the BO within the time τ₂- τ₁, provided the conditions (3) and (4) are satisfied, will result in that the characteristics of the spin structure produced by the BO will tend to become the same as those of the spin structure produced by the ULD. (From this viewpoint, one can speak of sensitivity of the BO to the action of ULD.)

The SPV model discussed makes it possible to explain the features of the effects of biologically active substances in ultra-low doses on biological objects, as observed in a lot of studies [4,5,22]:

1. The kinetic paradox: the effect of an ULD of a BAS on a cell or an organism is the strongest when the latter contain the same substance but in doses that are some orders of magnitude greater than the ULD used.

2. A change in sensitivity (generally, an increase) of the BO with respect to a subsequent exposure to a BAS in an ultra-low dose.

3. Dependence of the “sign” of the effect (inhibition or stimulation) on the initial state of the BO being treated.

4. A non-monotonic, polymodal (”oscillatory”) dose-response (or dose-effect) dependence. In most cases the activity maxima are observed within definite ranges of doses, which are separated by so-called dead zones. In some cases, the same effects are produced by doses of biologically active substances differing in 5 to 8 orders of magnitude. There are also cases where a change in the “sign” of the effect is observed in the dose dependence.

5. Disappearance of side effects with a decreased dose of BAS (but with persisting activity of the BAS in ULD).

Let us show that the above features of effects of BAS in ULD on BO can be explained by the properties of spin supercurrents emerging between the spin structures in the SPV.

1. The kinetic paradox

Note that condition (3) is always valid for the BAS which has been already contained in the BO but in a dose some orders of magnitude higher than the ultra-low dose used. The high concentration of such a substance in the BO results in that the spin structure produced by the BO in the SPV will have the characteristics determined by the properties of the substance, in particular, resulting in the minimum difference between the frequencies ω₂ τ₁ and ω₁ τ₁.

2. A change in sensitivity (generally, an increase) of the BO with respect to a subsequent exposure to a BAS in ULD.

According to (7), the action of a BAS in ULD on a BO results in that the frequency of precession in the spin structure produced by the BO changes. The change may result in that in the action of a second ULD on the same BO the BO sensitivity with respect to the second ULD will depend on the properties of the first ULD. Indeed the condition (3) may become invalid for the second ULD while it was valid before the action of the first ULD. Or, on the contrary, condition (3) may become valid for the second ULD although it was not valid before the action of the first ULD.

Let us consider the case where the frequency of precession in the spin structure produced by the first ULD (which was designated above

As ω₁ τ₁) is equal to the precession frequency in the spin structure produced by the second ULD. As follows from (7), after the action of the first ULD on the BO over the time τ₂- τ₁ the quantity Δω = ω₁ τ₁-ω₂ τ₂ (used in condition (3)) becomes of a smaller order of magnitude than it was before the action of the first ULD when it was equal to ω₁ τ₁ - ω₂ τ₁. This increases the sensitivity of the BO to subsequent actions of an ULD of BAS whose spin structure has the same precession frequency ω₁ τ₁ as that of the first ULD.

3. The dependence of the “sign” of the effect on the initial state of BO.

In point 1 above, the action of an ULD of BAS on a BO over the time τ₂- τ₁ results in that, under (7), the frequency of precession associated with the BO changes by the quantity ω₂ τ₂ - ω₂ τ₁. Consequently, taking into account (1), the energy of the spin structure produced by the BO in the SPV (and, as may be supposed, the energy of the object itself) will change by ΔU as follows:

(8)

Where S is the total spin of the spin structure produced by BO in the SPV.

Thus depending on the sign of ω₂ τ₂ - ω₂ τ₁ biologically active substances can be classified into two categories: “cooling” and “heating” with respect to the specific BO. If at time τ₁ the difference between the precession angles Δα τ1 is determined by (6), then, according to (7) and (8), at ω₂ τ₁ < ω₁ τ₁ the energy flow occurs towards the BO, and at ω₂T₁ > ω₁ τ₁ the direction of energy flow is opposite. According to (2), (6) and (7), the direction of energy flow is the same as that of the spin supercurrent.

In the general case, as follows from (5) and (2), the sign of spin supercurrent (J) τ₁ determining its direction at time τ₁ depends not only on the difference ω₂ τ ₁ - ω₂τ₁, but on the magnitude and the sign of Δα₀. It can be assumed that the sign of spin supercurrent determines the “sign” of the effect of ULD of BAS on the BO.

4. A non-monotonic, polymodal dose-effect curve; in some cases a change in the “sign” of the effect.

Let us examine the action of a BAS in ULD on a BO provided the ULD consists not of a single “quantum”, as in the above cases, but of Z “quanta”. Let j_i be the spin supercurrent between the spin structures produced by the i-th “quantum” of the ULD and the BO. Then the total spin supercurrent, J_sum caused by all “quanta” will be determined by the expression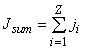

. Assuming that for every i the spin supercurrents j_i are equal to each other in both magnitude and sign, namely, j_t = j, then:

Jsum = Z . j . (9)

According to the properties of the spin supercurrents, there will be slippage of the angle (phase) of precession by the value of 2πn (n = 1, 2…) at a certain Δα_c and respective J_c. Taking into account (9), we shall introduce the critical value of the number of “quanta”, Z_c, at which the quantity J_sum takes the value of J_c whereby a slippage takes place:

(10)

As follows from the experiments whose results are shown in Figures 4a and 4b the dependence of spin supercurrent j on Δα is nonmonotonic and polymodal. The phase slippage may lead to a change in the sign of the spin supercurrent (Figure 4a) and thus to a decrease of the latter (Figure 4b). This makes both the value of Z_c and the sign of the effect variable for the same pair “ULD–BO”. Therefore, the phase slippage phenomenon makes the dependence of the total spin supercurrent between the spin structures produced by BAS in ULD and the BO on the number of “quanta” non-monotonic and polymodal.

5. The disappearance of side effects with a decreased dose of BAS (but with persisting activity of the BAS).

According to the definition of “quantum” introduced in this work, a quantum is such a dose of substance which produces in the SPV a spin structure with a single precession frequency of spins of microparticles that constitute the SPV, that is, under the notation introduced earlier,the frequency ω_1t. If the dose consists of several quanta, this means that the spin structure produced in the SPV by the BAS used is characterized by several values of ω_1t and, accordingly, may affect simultaneously several biological objects for which conditions (3) and (4) are satisfied. That is, the less the dose, the less the number of biological objects that interact with the BAS in ULD.

Discussion

The interaction of quantum objects through spin supercurrents is performed on a level different from the molecular one, namely, in the superfluid physical vacuum. Therefore, spin supercurrents cannot be shielded by molecular substances. This property of spin supercurrents agrees with the evidence given in the book by P. Bellavite and A. Signorine “The Emerging Science of Homeopathy” [23]: “There is some preliminary evidence demonstrating a homeopathic effect not only of solutions but also of closed ampoules containing solutions and placed in contact with the system to be regulated (human or animal).”

It follows from the above that an organism can “infect” another organism, although the “disease” is absolutely non-contagious from the standpoint of medical science. This contagious effect may take place due to an interaction between a sick organ of one organism and a healthy organ of another organism provided the organs produce spin structures in the SPV having closely spaced frequencies of precession. However, a sanative effect can take place as well if the interaction gives rise to the appropriate change in the characteristics of the spin structures produced by the sick organ. It is well known that up to the 19^th century it was a common belief that one could get rid of a disease by “transferring” it to an animal. For example: according to J. G. Frazer, the famous ethnologist, the “ancients held that if a person suffering from jaundice looked sharply at a stone-curlew, and the bird looked steadily at him, he was cured of the disease” [24].

Since there is a spin structure for any quantum object in physical vacuum, low-density streams of quantum particles (electrons, neutrons, protons, etc.) can act on a biological object as a BAS in ULD. The study of effects of such streams on a biological object is an efficient way of determining the precession frequency of spins in the spin structure produced by the biological object in physical vacuum ( the BO spin structure precession frequency has been denoted as Ñ 2t). This is due to the simplicity of determining the precession frequency of spins in the spin structure produced by a quantum particle in physical vacuum. Under the SPV model, this frequency is equal to E âï¿½ï¿½ Ä§, where E is the particle energy. Under equation (3), the effect of a quantum particle is maximum if ω_2t ≈ E âï¿½ï¿½ Ä§.

Electromagnetic radiation consists of quantum entities, photons, and consequently, according to the SPV model, produces in physical vacuum spin structures that may interact with the spin structures of biological objects. It was empirically established that the effects characteristic of the action of ULDs of biologically active substances on biological objects take place as well at the action of low-intensity EM radiation [4]. (Electromagnetic radiation is referred to as a lowintensity radiation if its flux density is less than 1 μW/cm².) Since spin supercurrents cannot be shielded by molecular substances, including the substances of which electromagnetic screens are made, a somewhat paradoxical, from the standpoint of mainstream physics, situation may arise: electromagnetic radiation, as producing spin supercurrents, can affect biological objects through electromagnetic screens.

A low-intensity EM radiation will produce an effect (in particular, a therapeutic one) on a BO provided the difference between the radiation frequency and the precession frequency of spins in the spin structure produced by the BO in the SPV meets the condition (3). A change in the above spin precession frequency means a change in the frequency of low-intensity EM radiation on which the radiation may produce an effect on the BO. (It is noteworthy that in the spin structure produced in the SPV by EM radiation there is a spin precession frequency equal to the frequency of the EM radiation.) Thus the study of effects of lowintensity electromagnetic radiation on a biological object, as well as the above mentioned study of effects of low-density streams of quantum particles, is an efficient way of determining the precession frequencies of spins in the spin structure produced by the biological object in physical vacuum.

According to the SPV model, spin supercurrents may arise between spin structures produced by any quantum objects in the SPV. This makes it possible for a BAS to effect a BO indirectly, through an intermediary which has acquired the properties of the BAS as a result of the preceding interaction with the latter.

That is, if there is an object or medium and the precession frequency of its spin structure becomes equal to that of the spin structure of the BAS as a result of interaction between the spin structures (in Section 3 the frequency is denoted as ω_1t), then the object or medium acquires a capacity to produce the same effect on the BO as the BAS. There are a number of experiments where the properties of water were affected by low-intensity electromagnetic radiation, weak magnetic fields, cosmophysical and geophysical factors of the environment [4,25], thus water can be considered to be such an intermediary.

According to the SPV model, the precession frequency of spins in the spin structure produced by a quantum object is determined by the energy of the object. But the energy of a quantum object determines as well the spectrum of its natural frequencies. Therefore, the spin precession frequency in the spin structure produced by a biological object (in Section 3 it is denoted as ω_2t) may coincide with one of the frequencies of the electromagnetic radiation of the object (ω'). Since according to the SPV model the frequency of a photon is equal to the frequency of precession of spins in the spin structure produced by it in physical vacuum, the effect of a flux of photons having frequency ω′ on such a BO will be the greatest because equation (3) will be met. This can elucidate the long-lived principle of treatment of various diseases: “Like cures like.” Here are some well-known recommendations based on that principle: erysipelatous inflammation having red color is treated by application of red cloth; choledochitis by yellow cloth. In fact, this principle is a manifestation of the ″kinetic paradox″ described in Section 3.

Conclusions

The effect of a biologically active substance (BAS) in ultra-low dose (ULD) on a biological object (BO) can be performed through spin supercurrents arising between spin structures produced by the BAS and the BO in physical vacuum having properties of superfluid ³He-B.

From the standpoint of the model of superfluid physical vacuum, the study of characteristics of spin structures (specifically, the spin precession frequencies) produced by a biological object in physical vacuum is best to perform as a study of effects of low-intensity electromagnetic radiation or low-density streams of quantum entities (neutrons, electrons, etc.) on the biological object.