Review Article Open Access
Plasma Diagnostics through Kinetic Modelling: Characterization of Matrix Effects during ICP and Flame Atomic Spectrometry in terms of Collisional Radiative Recombination Activation Energy–A Review
Mark Fungayi Zaranyika1* and Courtie Mahamadi2
1 Chemistry Department, University of Zimbabwe, Zimbabwe
2 Chemistry Department, Bindura University of Science Education, Bindura, Zimbabwe
- *Corresponding Author:
- Mark Fungayi Zaranyika
Chemistry Department, University of Zimbabwe
P. O. Box MP 167 Mount Pleasant
Harare, Zimbabwe
E-mail: Zaranyika@science.uz.ac.zw
Received date: August 12, 2013; Accepted date: September 19, 2013; Published date: September 23, 2013
Citation: Zaranyika MF, Mahamadi C (2013) Plasma Diagnostics through Kinetic Modelling: Characterization of Matrix Effects during ICP and Flame Atomic Spectrometry in terms of Collisional Radiative Recombination Activation Energy–A Review. J Anal Bioanal Tech 4:173. doi: 10.4172/2155-9872.1000173
Copyright: © 2013 Zaranyika MF, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Analytical & Bioanalytical Techniques
Abstract
Inductively coupled plasma atomic emission spectrometry (ICP-AES) is one of the most widely used and extremely important tools for trace element analysis today. The technique however still suffers from matrix effects, especially those due to easily ionizable elements (EIEs). Current theory of atomic spectrometry assumes Local Thermal Equilibrium (LTE), and EIE interference effects cannot be explained fully as long as all the electrons in the plasma are regarded as equivalent in accordance with the LTE theory. If however it is assumed that electronic collisions with heavy particles can occur before or after thermal equilibration, then electrons can be expected to experience different activation energies depending on whether collisions occurred before or after thermal equilibration. This paper reviews recent work carried out to characterize EIE interference effects during ICP-AES, flame AAS and flame AES in terms of ion-electron collisional radiative recombination activation energy. The work is based on a simplified rate model showing that when analytes are determined by atomic spectrometry in the absence and then in the presence of EIEs as interferents, the change in collisional radiative recombination activation energy, ΔEa, is zero when the system conforms to LTE. Several analyte-interferent systems have been studied, and results obtained so far lead to the conclusion that departure from LTE results from collisions involving electrons in the ambipolar diffusion state. Factors affecting both pre-LTE and LTE collisions, as well as a possible collisional radiative recombination mechanism designed to account for the ΔEa values obtained are discussed.
Keywords
Matrix effects; Inductively coupled plasma atomic spectrometry (ICP-AES); Local thermal equilibrium; Plasma diagnostics; Radiative recombination; Easily ionizable elements; Activation energy
Introduction
The inductively coupled argon plasma was introduced as an excitation source during the 1960s and 1970s [1]. Its major characteristics are very high temperature (6000-10000 K) and high electron number densities (10-15-10-16 cm-3s-1) [1,2]. The other attributes of ICP-AES are multi-element capability, and superiority with respect to accuracy, precision, detection limits, dynamic range, and relative freedom from interference than other analytical instrumental techniques [1]. The technique however suffers from inter-element effects, in particular matrix effects due to elements with low ionization potentials (IP), known as easily ionizable elements (EIEs) [3]. Current theory of atomic spectrometry assumes local thermal equilibrium (LTE) [1]. According to this theory, all equilibriating processes within the plasma are due to collisional processes, and the contribution from radiative processes is negligible. All processes interfering with analyte excitation and ionization should be explainable in terms of the theory. In practice it is found however that matrix effects due to EIEs in the ICP cannot be explained easily using the theory, and it is now generally accepted that the ICP is not in local thermal equilibrium [1-3].
A gaseous system in complete thermal equilibrium, TE, is characterized by a number of distributions that are sensitive functions of temperature, namely, the Maxwell velocity distribution law, Boltzmann population distribution law of bound states, the Saha-Eggert population distribution of ionization products, the Guldberg-Waage distribution of dissociation products, and Planck’s radiation distribution law [1,4]. Maxwell’s distribution law defines the plasma temperature, T; while the Saha-Eggert and Gulberg-Waage distributions can be viewed as statements of the law-of-mass-action. Local thermal equilibrium, LTE, allows for spatial decoupling of temperature, and decoupling of energy and matter, while partial thermal equilibrium, p-LTE, allows for decoupling of electrons and heavy particles. Because of their smaller mass, the heating of electrons in a plasma is much faster than transfer of energy from electrons to heavy particles, hence a two-tier temperature plasma is established, electrons with a higher Maxwellian distribution temperature (the electron temperature, Te), and heavy particles with a lower temperature (the gas temperature, Tg). In addition, the assumption of LTE subsumes that, following ionization, electrons are released with kinetic energy equal to the ionization potential of the respective atom, but quickly lose this energy through thermal collisions so that at thermal equilibrium all the electrons will have kinetic energy equal to kTe, where k is the Boltzmann constant [5].
Because of the relatively high temperature of the ICP, it is generally accepted that in the ICP, EIE’s interfere with the excitation and/or ionization of the analyte [6]. Excitation and de-excitation processes in atomic spectrometry have been reviewed by several workers [1-4,7-10]. Major excitation and de-excitation processes that have been proposed include thermal excitation [5]; electron collisional excitation [1,2]; electron-ion radiative recombination [11-14]; excitation via charge transfer [5,15-17]; radiative relaxation [1,2,5]; electron collisional deexcitation [2,5]. A study of the effects of EIE’s on analyte atomic and ionic line absorbance and emission intensity should therefore lead to an understanding of the processes that are responsible for populating or depopulating analyte atomic and ionic excited states. This paper reviews the progress made to date towards understanding why the ICP is not in thermal equilibrium.
Plasma Diagnostics: Active and Passive Spectroscopic Methods
Techniques for studying the effect of interferents on the emission intensity of analyte atomic and ionic lines in atomic spectrometry have been reviewed by Hieftje et al. [18,19]. They comprise active spectroscopic methods, passive spectroscopic methods and kinetic modeling methods. Active spectroscopic methods involve irradiating plasma particles with electromagnetic radiation and observing the radiation they emit. Key parameters in this approach to plasma diagnostics are the electron number density (ne), electron temperature (Te), the gas kinetic temperature (Tg) and the argon atom number density (nAr). The methods employed involve a combination of Thomson scattering [20-25], Rayleigh scattering, computed emission topography [26-28] and laser-induced saturated fluorescence [29,30]. Thomson scattering enables measurement of Te and ne. The intensity of the Rayleigh scattering is proportional to nAr, which in turn is inversely proportional to Tg. Computed emission tomography enables the display of the full three-dimensional structure of the plasma torch [18,19]. Laser-induced saturated fluorescence yields time-resolved spatial maps of ground state analyte atoms and ions, as well as argon excited states [29,30]. Passive spectroscopic methods simply observe the radiation emitted by the plasma [18,19,31], and have been used to study (a) vertical and radial profiles of interference effects, (b) the effects of varying the interferents, (c) effect of varying rf power, (d) nebulizer effects, and (e) shifts in ionization equilibria [2,32-36].
The combination of active and passive spectroscopic plasma diagnostic methods has yielded a lot of information about the spatial variation of the composition of the plasma, spatial variation of interference effects, the effects of varying radio frequency (rf) power. In addition, considerable success has been achieved in the determination of the electron number density (ne), electron temperature (Te), the gas kinetic temperature (Tg) and the argon atom number density (nAr). Results from active spectroscopic studies in general confirm that the ICP is dominated by electrons from the ionization of Ar, so that matrix effects due to EIEs cannot be explained fully on the basis of the results from active and passive plasma diagnostic methods, leading researchers to conclude that the ICP is not in LTE [3,37-41].
Plasma Diagnostics: Reaction Rate Methods
Classical collisional-radiative rate model approach
The use of reaction rate models to probe excitation and deexcitation reactions occurring in the plasma has been attempted by several workers [42-56], two approaches are employed: the Classical Collisional-radiative Rate Model approach and the Simplified Collisional-radiative Rate Model approach. Both models assume steady state kinetics within the plasma. The classical collisional-radiative rate model approach takes into account all possible electronic states of the analyte and matrix, with the level populations being derived from the excitation and de-excitation reactions occurring in the plasma. Several authors have derived steady-state kinetic equations to describe matrix effects during ICP-AES using the classical reaction rate model [48-51]. The models derived are extremely complex, such that arriving at solutions is difficult [18]. Classical models have therefore not met with much success.
Simplified collisional-radiative rate model approach
Simplified collisional-radiative rate models focus on only one atomic level of the analyte. Two approaches have been proposed: (a) correlation of analyte emission with localized concentration maps of the analyte in the absence and presence of interferent species (Hieftje et al. [19,52,53]), and (b) theoretical simulation of the signal enhancement ratio in the analytical zone of the plasma in the presence of EIEs [56-60].
Simplified Collisional-radiative Rate Model Approach: Correlation of Analyte Emission with localized Analyte Concentration Maps
Correlation of analyte emission with localized concentration maps of the analyte in the absence and presence of interferent species exploits the heterogeneous spatial character of the plasma. Under steady-state conditions, each excitation model predicts proportionality between atomic or ionic emission and localized concentrations of species involved in the excitation process. Hieftje et al. cite Ca as an example [19]. Assuming Ca is excited by the recombination of Ca+ and an electron, e-, and assuming steady state kinetics, the excitation can be represented as follows:
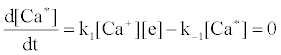
Hence
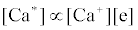
where k1 and k-1 are rate constants. As a result, models can be tested by comparing spatial emission behavior with experimental maps of reactant concentration and partners (or products of such maps) which the model assumes are important. Generally, a specific mechanism of excitation or ionization is first proposed and corresponding steady-state kinetic expression developed. This hypothesis is then tested through the use of the derived steady-state relationships and appropriate experimentally developed parameters and spatial maps. The technique was recently reviewed by Hieftje et al. [19], who concluded that a great deal still remains unknown about the analytical ICP and the events that occur in it. Further work was still needed to establish a clearer understanding of how inter-element interferences arise. On the other hand, considerable success has been achieved with simplified rate models based on simulation of signal enhancement factor in the analytical zone of the plasma. A detailed review of this work is therefore given in the sections that follow.
Simplified Collisional-radiative Rate Model based on Emission Enhancement Factor Theoretical basis
Zaranyika et al. [54,56] proposed a simplified reaction rate model that focuses on only one particular electronic level for the effect of EIEs in the air-acetylene flame and the ICP. Along with the simplified model, they proposed a novel method for probing changes in the number density of the analyte ground state and excited state, no and nu respectively, based on determining the analyte absorbance (A) and emission (I) signal ratios A’/A and I’/I respectively, where the prime denotes presence of interferent, and comparing to theoretical values, no’/no and nu’/nu, derived assuming a simplified rate model based on steady state kinetics in the plasma. The approach assumes no change in the rate of introduction of analyte atoms into, and no change in the temperature of the torch or flame, upon the simultaneous introduction of an easily ionized interferent element. The argument by the authors is that according to the LTE approach, atomic line absorption and atomic line emission intensities are directly proportional to the population of the ground and excited states, respectively, i.e., A ∝ no and I ∝ nu, where A is the absorption signal intensity and I is the line emission signal intensity, and no and nu are the atomic populations of the ground and excited states, respectively. nu and no are related by the Boltzmann equation:
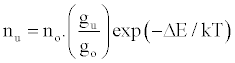 (1)
(1)
and
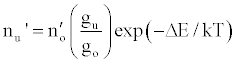 (2)
(2)
or
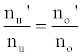 (3)
(3)
Hence,
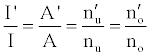 (4)
(4)
Where the prime denotes quantities measured in the presence of an interferent, gu and go are the statistical weights of the excited and ground states, respectively, k is the Boltzmann constant, T is the absolute temperature and ΔE is the difference in the energies of the two electronic states involved in the transition. Eq. 2 assumes the rate of introduction of the analyte atoms into the plasma is kept constant, and no change in the plasma temperature on simultaneous introduction of interferent metal atoms. On the basis of Eq. 4, the effects of collisional processes on the excitation, ionization and line emission of the analyte atoms resulting from the presence of interferent atoms are followed by measuring the absorption or emission intensities of a given concentration of analyte atoms in the absence and presence of the interferent, and comparing the I’/I and A’/A ratios to each other, and to unity, as shown in Table 1.
| Observation | I’/I value | Example of collisional process |
|---|---|---|
| Signal enhancement | >1 | Increase of ground state, e.g. suppression of ionization; Increase in excited state, e.g., ion-electron collisional radiative recombination. |
| Signal depression | <1 | Depopulation of ground state, e.g. charge transfer reactions; Depopulation of excited state, e.g., collisional de-excitation |
| No effect on signal | 1 | No change in the populations of the ground and excited states of analyte atoms |
Table 1: Matrix interference effects and corresponding I’/I values expected during atomic emission spectrometry.
An alternative approach also employed is plotting theoretical curves of nu’/nu, derived on the basis of an assumed mechanism and assuming steady state kinetics within the plasma, as a function of analyte concentration and comparing the curves with the experimental I’/I. The validity of the assumed mechanism is indicated if there is close agreement between the two curves.
Experimental Design
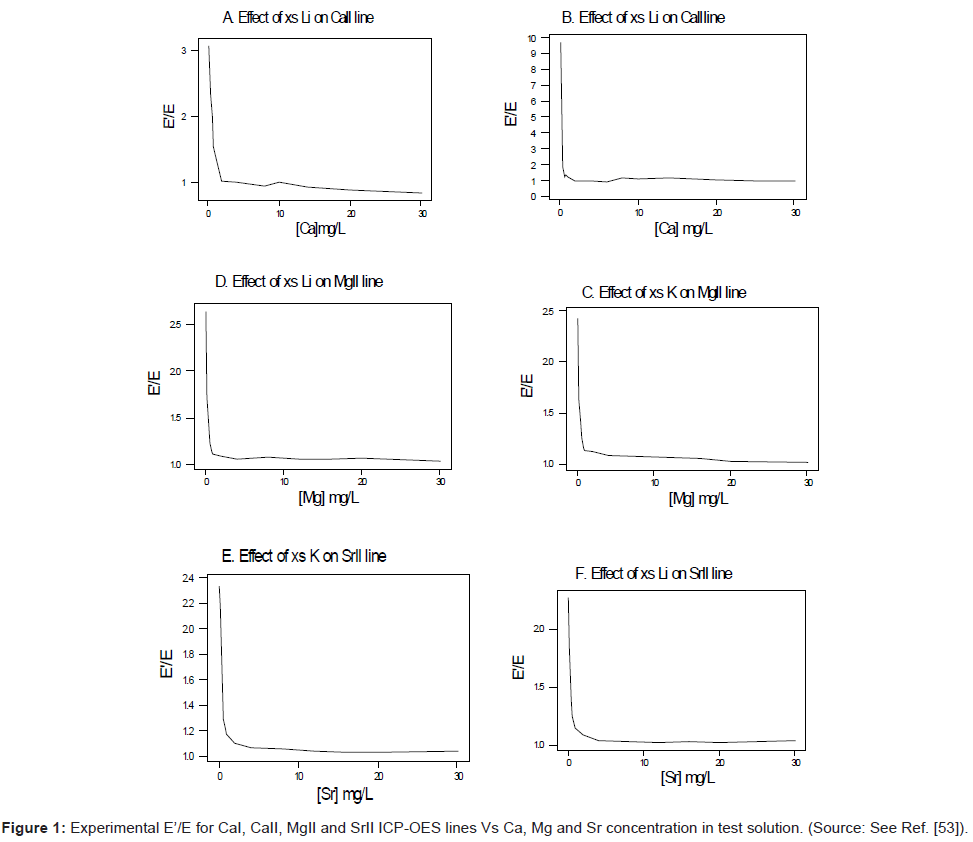
In terms of experimental design, high purity reagents are used. Two sets of standard solutions containing 0 to 30-mg/L analyte are prepared [54-56]. One set is spiked with 1000 mg/L of easily ionizable interferent (Li, K or Na). The other set is left unspiked. In order to minimise changes in the physical properties of the test solution upon the introduction of the interferent, the interferent concentration is kept constant at a very high level (1000 mg/L) relative to that of the analyte (0-30 mg/L), whilst the analyte concentration is varied. Under these conditions any effect due to the changes in the physical properties of the test solution in going from the interferent-free solution to the interferent-spiked solution will affect the series of interferent-spiked solutions to the same extent, and this can be compensated for by taking blank readings of a solution containing the interferent salt only. Emission and/or absorbance readings are made in triplicate and corrected for the blank readings. The ratios I’/I are calculated and plotted as a function of the analyte concentration in the test solution. Figure 1 shows typical plots obtained for the ICP [56]. Similar plots were obtained for flame experiments in the emission and absorbance modes [54-56].
Theoretical calculations
Preliminary experiments are run to determine the aspiration rate and the nebulization efficiency for the type of solutions under analysis [54-56]. Theoretical nu’/nu ratios are calculated using rate equations derived assuming steady state conditions within the plasma, and number densities based on the experimentally determined aspiration rate, nebulization efficiency and plasma temperature values. The degree of ionization for analytes and interferents are based on the Saha equation [61], otherwise literature values are used [1,62-64]. Table 2 shows typical number density values obtained for ICP and flame experiments involving Group II analytes and I interferents [58,59].
| M* | FAES | ICP-AES | |||
|---|---|---|---|---|---|
| MI | MII | MI | MII | MIII | |
| Ca | 2.5147×1010c** | 2.46×1010c | 1.5818×109c | ||
| Mg | 2.4058×1011c | 1.2029×109c*** | 4.1004×1010c | 3.8134×1010c | 2.452×109c |
| K | 1.7808×1011 | 1.9589×109c | |||
| Sr | 1.1377×1010c | 1.1309×1010c | 2.2301×109c | ||
| Ar | 2.6883×1019 | 2.9242×1016 | |||
| Li | 1.4367×1014 | 1.4367×1014 | |||
| K | 1.7808×1014 | 1.9589×1012*** | 2.5495×1013 | 2.5495×1013 | |
| Na | 3.0287×1014 | 2.8167×1013*** | |||
M*=element; **c=concentration in test solution (mg/L), ***Degree of ionization, α=0.005 (Mg), 0.011 (K), 0.093 (Na); Atomization efficiency, β=84% (Mg) [63].
Table 2: Typical flow number densities (atoms/ions cm-3s-1) in the ICP.
Simplified Collisional-radiative Rate Model based on Emission Enhancement Factor
Review of Progress to date
Use of signal enhancement curves: Zaranyika and his co-workers have used this simplified rate model approach to study several systems, both flame and ICP. When the model was applied to the effects of excess Na on emission of K during air-acetylene flame emission spectrometry [54], the results confirmed overpopulation of the excited state in terms of the Boltzmann equation, below analyte concentrations in the test solution of about 1 μg/mL. Over population of the ground state was also observed when observations were made from the primary reaction zone of the flame in the same test solution analyte concentration range. Minimal emission and absorbance signal enhancement was observed above about 1 μg/mL analyte concentration in the test solution. At higher analyte concentrations in the test solution, about 20 to 30 μg/ mL, signal depression was sometimes observed. These trends were observed for several different analytes [55,56].
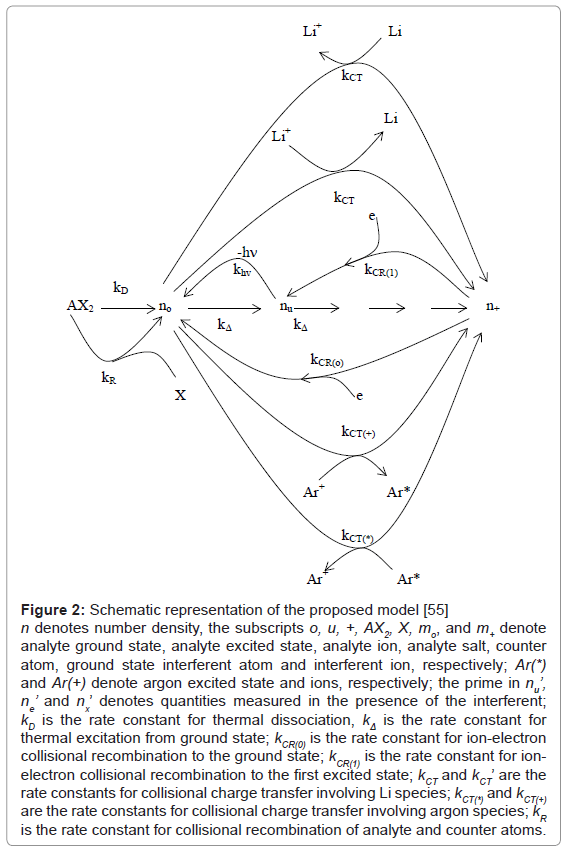
Kinetic modeling of the signal enhancement curve: Kinetic modeling of the signal enhancement curve has also been attempted. In this approach, the I’/I or A’/A experimental values are compared to theoretical nu’/nu or no’/no values derived assuming steady state conditions within the plasma, and taking into the various collisional processes that are likely to significantly affect analyte ground state, excited state and ionic state populations. Several analyte/interferent systems have been studied using this approach using air-acetylene FAES and FAAS [54-56]. More recently studies have been conducted using ICP-AES. In one such a study of the effects of excess Li on Ca in the ICP, Zaranyika and Chirenje [56], proposed the kinetic scheme shown in Figure 2, in which n denotes number density, the subscripts o, u, +, AX2, X, mo, and m+ denote analyte ground state, analyte excited state, analyte ion, analyte salt, counter atom, ground state, interferent atom and interferent ion, respectively; Ar(*) and Ar(+) denote argon excited state and ions, respectively; the prime in nu’, ne’ and nx’ denotes quantities measured in the presence of the interferent; kD is the rate constant for thermal dissociation, kΔ is the rate constant for thermal excitation from ground state; kCR(0) is the rate constant for ion-electron collisional recombination to the ground state; kCR(1) is the rate constant for ion-electron collisional recombination to the first excited state; kCT and kCT’ are the rate constants for collisional charge transfer involving Li species; kCT(*) and kCT(+) are the rate constants for collisional charge transfer involving argon species; kR is the rate constant for collisional recombination of analyte and counter atoms.
Figure 2: Schematic representation of the proposed model [55] n denotes number density, the subscripts o, u, +, AX2, X, mo, and m+ denote analyte ground state, analyte excited state, analyte ion, analyte salt, counter atom, ground state interferent atom and interferent ion, respectively; Ar(*) and Ar(+) denote argon excited state and ions, respectively; the prime in nu’, ne’ and nx’ denotes quantities measured in the presence of the interferent; kD is the rate constant for thermal dissociation, kΔ is the rate constant for thermal excitation from ground state; kCR(0) is the rate constant for ion-electron collisional recombination to the ground state; kCR(1) is the rate constant for ionelectron collisional recombination to the first excited state; kCT and kCT’ are the rate constants for collisional charge transfer involving Li species; kCT(*) and kCT(+) are the rate constants for collisional charge transfer involving argon species; kR is the rate constant for collisional recombination of analyte and counter atoms.
The model took into account (a) the relative rates of thermal dissociation of analyte salt, (b) collisional recombination of counter atom and analyte atoms, (c) charge transfer between analyte and argon species and (e) ion/electron collisional recombination. The various rate constants were estimated using collision theory. The degree of ionization was calculated using the Saha relationship [61]. For Ca and Li the values obtained were in excess of the ground state number densities, implying 100% atomization and virtually 100% ionization, so that the contribution of thermal dissociation, analyte ion/ counter atom recombination, and charge transfer involving analyte or interferent ground state to the observed interference effects become negligible.
By assuming steady state conditions with respect to the number density of analyte excited state atoms, nu, and ground state atoms, no, the authors showed that the ratio of the number density of analyte atoms in the excited state in the presence of the interferent, nu’, to that in the absence of interferent, nu, was given by:
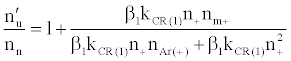 (5)
(5)
or
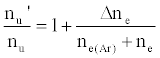 (6)
(6)
where β1 is the fraction of analyte ions undergoing collisional radiative recombination to the first excited state, Δne=nm+, the change in electron number density within the plasma upon the addition of the interferent to the analyte solution.
As discussed above, the experiment was designed so that ne(Ar) >> ne, meaning Eq. 6 reduces to
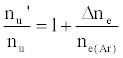 (7)
(7)
i.e., nu’/nu=a constant.
This was contrary to experiment as shown in Figure 1, suggesting that the contribution of collisional radiative recombination involving electrons from the ionization of Ar to the observed interference effects was negligible under the conditions of the experiment, and Eq.6 reduces to:
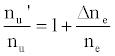 (8)
(8)
Equation 8 gave a curve similar to the experimental curve [56]. Numerical results above 1 μg/mL analyte concentration in the test solution were in good agreement with experiment, but results below about 1 μg/mL were up to 2 orders of magnitude higher than experiment. Factoring in collisional de-excitation of excited analyte atoms and collisional ionization of analyte excited state atoms, which had not been taken into account in the formulation of the model, had little or no effect on the results. The deviation of the experimental from the theoretical curve lead the authors to conclude that only a fraction of electrons from the ionization of the interferent were involved in collisional radiative recombination to give analyte excited state atoms.
The work by Zaranyika and Chirenje [56] made some important findings, namely:
a. Those electrons from the ionization Ar were not involved in collisional processes leading to the observed emission signal enhancement.
b. That the observed interference effects could be attributed to ionelectron collisional recombination.
c. That the contribution of thermal excitation was negligible.
d. That not all the electrons from the ionization of the interferent EIE were involved in collisional effects leading to excitation of the analyte.
At this stage what remained to be explained were the apparent non-involvement of electrons from the ionization of Ar in collisional processes leading to the observed interference effects, and why not all the electrons from the ionization of the EIE were involved in the collisional processes leading to the observed interference effects.
Departure from LTE: Characterization in terms of Collisional Radiative Recombination Activation Energy
To tackle the problem of the non-involvement of Ar species in collisional processes leading to the observed emission signal enhancement, Zaranyika et al. [58-60] invoked ambipolar diffusion as the possible source of the discrepancy. Ambipolar diffusion is common plasmas [5], and is defined as the state of charge separation balance in which ions and electrons diffuse with the same velocity. In the ambipolar diffusion state, electrons have kinetic energies equal to the ionization potentials of the parent atoms or ions. The number density of electrons in the ambipolar diffusion layer will depend on the ionization potential of the ion and temperature of the plasma [5]. Zaranyika and co-workers assumed that collisional radiative recombination with analyte ions involves an ion-electron activated transition state, and that collisional radiative recombination can occur before or after thermal equilibration. If this was the case, the authors argued that the electron should experience different activation energies depending on whether collisions leading to the observed interference effects occurred before or after thermal equilibration, i.e., the rate constants kCR(1)’ and kCR(1) in Eq. 5 no longer cancel out. Equation 8 was modified to Eqs 9 and 10 in order to reflect this:
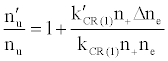 (9)
(9)
or
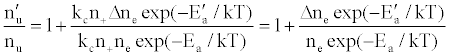 (12)
(12)
or
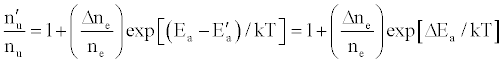 (13)
(13)
where Ea and Ea’ are the activation energies experienced by electrons from the ionization of the analyte and interferent respectively, Δne=nm+, and nm+ represents the number density of interferent ions; and
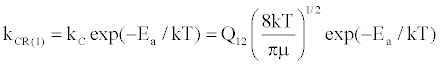 (14)
(14)
where Q12 is the collision cross-section between particles 1 and 2, and μ is their reduced mass.
The authors showed that three limiting cases can be defined for Eq. 11 on the basis of whether collisional radiative recombination occurs before or after thermal equilibration as shown in Table 3. Table 3 assumes that upon ionization, electrons are released with kinetic energy (KE) equal to the ionization potential (IP) of the parent atom or ion. After thermal equilibration, the electron will have KE=kT.
| Limiting Case (LC)a | Designation | ΔEa Expressionb | ΔEa theoretical valueb |
|---|---|---|---|
| LC 1A | LTE | Ea = Ea’ | 0 |
| LC 1B | Pre-LTE | IPm - IPa | IPm - IPa |
| LC 1C | Pre-LTE (analyte) LTE (interferent) |
kT -IPa | kT -IPa |
aSee Ref. [60], bSubscripts a and m denote analyte and interferent respectively, IP = ionization potential
Table 3: Theoretical ΔEa values under LTE and pre-LTE collisional radiative recombination conditions.
The authors assumed that upon collisional radiative recombination, if the distribution of recombining electrons into the various levels is such that the Boltzmann law for bound states is maintained, then Eq. 3 holds, so that Eq. 11 applies to emission as well as absorbance measurements. The authors assumed further that Eq. 4 holds, so that a plot of experimental I’/I, or A’/A, ratios versus Δne/ne in Eq. 11 should yield a linear graph of a slope from which the change in activation energy can be calculated, and compared to theoretical values as predicted by Limiting Cases IA to IC in Table 3. Table 4 shows the regression data and the experimental ΔEa values obtained when various analyte/interference systems were studied in the ICP [58,59] as well as the air-acetylene flame [60].
| Analyte* | M* | Slope | Intercept | R2 | ΔEa (Expt) | ΔEa (Theoretical, eV)** | ||
|---|---|---|---|---|---|---|---|---|
| LC 1A | LC 1B | LC 1C | ||||||
| (a) FAAS experiment | ||||||||
| MgI | Ca | 6.34×10-4 | -1.5168 | 0 | -0.721 | -5.335 | ||
| MgI | Sr | 4.84×10-4 | -1.6924 | 0 | -1.952 | -7.422 | ||
| (a) FAES experiment | ||||||||
| Mg(I) | K | 4.43×10-5 | 1.14648 | 0.851 | -2.223 | 0 | -3.306 | -7.646 |
| K(I) | Na | 2.91×10-5 | 1.21180 | 0.798 | -2.316 | 0 | +0.798 | -4.341 |
| (b) ICP-AES: Atom line: ne = nMII | ||||||||
| CaI | Li | 2.50×10-4 | -6.62 | 0 | -.0721 | -5.335 | ||
| (c) ICP-AES: Ion line: ne = nMIII | ||||||||
| CaII | Li | 1.83 | -9.83 | 0 | -6.478 | -11.09 | ||
| MgII | Li | 1.51 | -13.52 | 0 | -9.641 | -14.26 | ||
| Mg(II) | Li | 1.32×10-5 | 1.01889 | 0.992 | -8.713 | 0 | -9.644 | -14.260 |
| Mg(II) | K | 1.51×10-5 | 1.00707 | 0.990 | -8.609 | 0 | -10.695 | -14.260 |
| Sr(II) | Li | 1.15×10-5 | 1.04741 | 0.979 | -8.820 | 0 | -5.638 | -10.254 |
| Sr(II) | K | 1.28×10-5 | 1.02957 | 0.913 | -8.737 | 0 | -6.690 | -10.254 |
| Ca(II) | Li | 4.25×10-6 | 0.95376 | 0.876 | -9.592 | 0 | -7.531 | -11.096 |
*Ionization potentials (eV): Mg1=7.64624, MgII=15.03528, SrII=11.03013, CaI= 6.11316, CaII=11.87172, LiI=5.39172, KI=4.34066, NaI=5.13908 [65], **LC= limiting case (see text): LC 1A=LTE, LC 1B=Pre-LTE, LC 1C=Pre-LTE(analyte)/ LTE(Interferent), CL = confidence level [59,60].
Table 4: Experimental and theoretical ΔEa values for various analyte/interferent systems in the ICP as well as air-acetylene flame plasma.
From Table 4 it is apparent that of all the systems studied, none conforms to LC IA, from which the authors concluded that radiative recombination involving analyte ions and electrons in the absence of the interferent, is always pre-LTE whether it is in the air-acetylene flame or the ICP. Analyte radiative recombination in the presence of interferents in flame systems was also always pre-LTE (i.e., LC IB), whereas in the ICP it can be pre-LTE or LTE (i.e., LC IB or LC IC). Another conclusion drawn from the data in Table 4 was that electrons from the ionization of Ar in the ICP do not seem to participate in the collisional processes leading to the observed interference effects. The only plausible explanation advanced for this was that collisions involving electrons from the ionization of Ar are always pre-LTE whereby the energy of the electrons at 15.755 eV (i.e., the ionization potential of Ar), is far in excess of that required for radiative recombination or collisional excitation. The authors however point out that electrons from the ionization of Ar can participate in collisional ionization of analyte atoms, but since the kinetic energy of the electrons from the ionization of Ar is in large excess of the ionization potential of both analyte and the interferent, the extend of such collisional ionization would be virtually the same in the absence or presence of the interferent.
Departure from LTE: Effect of Ionization Potential and Plasma Temperature on free Electron Number Density
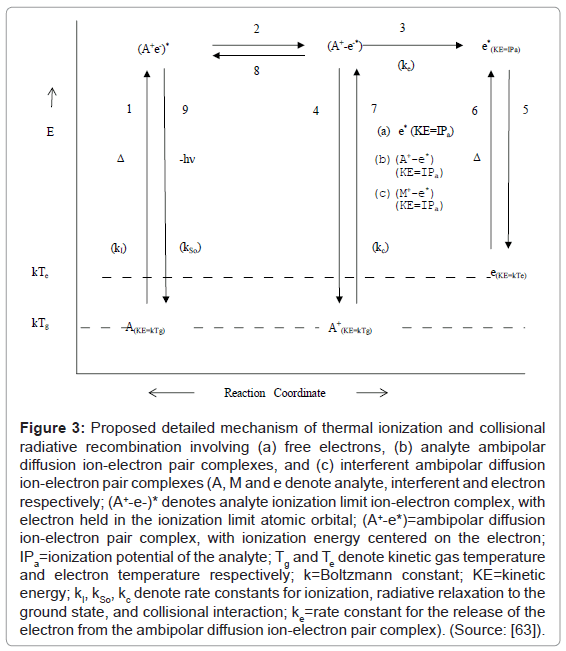
Zaranyika et al. explained the results obtained in the experiments reviewed above in terms of ambipolar diffusion. In the ambipolar diffusion state, the ion and electron behave as an ion pair, and the electron is not completely free and therefore not capable of random motion. It would appear from the results presented above that the number density of electrons in the ambipolar diffusion layer bears an inverse relationship to both ionization potential of the parent atom/ion and plasma temperature. Accordingly, the Zaranyika and co-workers proposed the scheme shown in Figure 3 [59] to illustrate the steps involved in ion-electron radiative recombination.
Figure 3: Proposed detailed mechanism of thermal ionization and collisional radiative recombination involving (a) free electrons, (b) analyte ambipolar diffusion ion-electron pair complexes, and (c) interferent ambipolar diffusion ion-electron pair complexes (A, M and e denote analyte, interferent and electron respectively; (A+-e-)* denotes analyte ionization limit ion-electron complex, with electron held in the ionization limit atomic orbital; (A+-e*)=ambipolar diffusion ion-electron pair complex, with ionization energy centered on the electron; IPa=ionization potential of the analyte; Tg and Te denote kinetic gas temperature and electron temperature respectively; k=Boltzmann constant; KE=kinetic energy; kI, kSo, kc denote rate constants for ionization, radiative relaxation to the ground state, and collisional interaction; ke=rate constant for the release of the electron from the ambipolar diffusion ion-electron pair complex). (Source: [63]).
Steps 1 to 5 relate to ionization, while Steps 6 to 9 relate to collisional radiative recombination.
Ionization: Involves thermal excitation of the atom to the ionization limit excited state (Step 1), followed by transfer of the internalized energy of excitation to the electron to give the ambipolar diffusion ion pair (Step 2), then ejection of the activated electron (Step 3), and simultaneous return of the ion to the LTE state (Step 4), and finally thermal de-activation of the electron and its relaxation to the LTE state (Step 5);
Collisional radiative recombination involving free electrons: Involves thermal activation of the electron (Step 6), followed by collision with the ion to give the ambipolar diffusion ion pair (Step 7), internalization of the activation energy of the electron to give the ionization limit excited state (Step 8), release of the potential energy of the electron as a photon, and relaxation of the atom to the LTE state (Step 9).
Collisional radiative recombination involving interferent ion-electron ambipolar diffusion ion pair complexes: Involves thermal activation of the interferent ion-electron ambipolar diffusion ion pair complex (Step 6), followed by collision with the analyte ion to give the analyte ambipolar diffusion ion pair (Step 7), internalization of the activation energy of the electron to give the ionization limit excited state (Step 8), release of the potential energy of the electron as a photon, and relaxation of the atom to the LTE state (Step 9).
Collisional radiative recombination involving analyte ion-electron ambipolar diffusion ion pair complexes: analyte ion-electron ambipolar diffusion ion pair complexes do not require activation, and Step 7 to 9 proceed as above.
In a recent paper, Zaranyika and Mahamadi showed that atomic excited states can be reached via thermal excitation from the ground state, or via radiative recombination directly to the excited state [59]. In addition these workers showed that thermal excitation is dominant only when the ground state is reached via radiative recombination, otherwise direct population of the excited state via radiative recombination is dominant. The Boltzmann distribution law for bound states is defined for thermal excitation from the ground state. Zaranyika and Mahamadi [59] argue that if it is assumed that during collisional radiative recombination, the distribution of recombining electrons into the various levels is such that the Boltzmann law for bound states is maintained, then it can be safely assume that kso and ks1, the rate constants for radiative relaxation to the so and s1 electronic states, have values equal to the inverse of the Boltzmann factors for the corresponding ionization processes. These are shown in Table 5.
| Reaction | Rate constant* |
|---|---|
| (a) M+(KE=kTg) +e*(KE=IP) → (M+-e*)(KE=IP) ↔ (M+e-)*(KE=IP) | 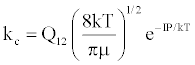 |
| (b) (M+e-)* → M+hn(so) | 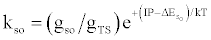 |
| (c) (M+e-)* → M+hn(s1) | 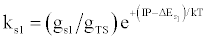 |
| (d) (M+e-)* → M+hn(si) | 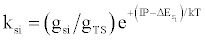 |
*kso and ks1 are the rate constants for radiative relaxation to the so and s1 electronic states, IP=ionization potential of M, and ΔEso, ΔEs1 and ΔEsi are the energy differences between the so, s1 and si electronic states with the ground state, so, and gsi and gTS are the statistical weights of the Si state and ambipolar diffusion ionelectron transition state, respectively (Source: See Ref. [63])
Table 5: Rate constants for Steps involved in collisional radiative recombination.
By regarding the ionization limit transition state, (M+e-)*, and the ambipolar diffusion ion pair, (M+--e*), in Figure 3, as resonance structures the authors were able t show that [59]:
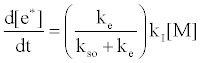 (13)
(13)
where kI=ionization rate constant, kso=rate constant for radiative relaxation to the ground state, ke=rate constant for release of free electrons. From Table 5 the rate constant for radiative relaxation, kso, increases with increase in ionization potential, leading to reduced rate of generation of free electrons. Similarly, kI increases with temperature, leading to an increase of Step 3 in Figure 3. This would explain why the ambipolar diffusion argon ion/electron transition state would be expected to have a longer lifetime than that of easily ionizable elements, which have much lower ionization potentials, and why an increase in temperature tends to reduce the lifetime of easily ionizable element ambipolar diffusion ion/electron transition state.
Departure from LTE: Implications with respect to the Boltzmann Distribution Law for bound States
Figure 3 represents the composition of the plasma with respect to a given atomic species, i.e., ground state atoms, ions and some electrons at LTE, ion-electron pairs and ‘hot’ electrons in the ambipolar diffusion layer at an energy level corresponding to the ionization potential of the atom above LTE. By assuming a steady state with respect to the ionization limit ion pair complex for process (b) in Table 5, Zaranyika and Mahamadi [59] showed that
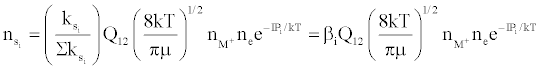 (14)
(14)
and
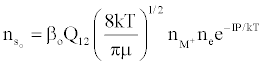 (15)
(15)
where βo and β1 are the fractions of electrons undergoing radiative relaxation to the ground state and excited state respectively, and kc is the rate constant for thermal activation of the free electron from the LTE state to the ionization limit state of the atom M. Therefore
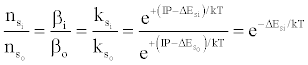 (16)
(16)
Or
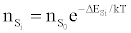 (17)
(17)
in agreement with the Boltzmann law (ΔEso=0). The authors interpreted this to mean that the Boltzmann law for bound states is obeyed even though the plasma is not in LTE.
Excitation during ICP-AES and flame AES: Contribution from electron collisional excitation
Electron collisional excitation was not taken into account in all the papers reviewed above. This can be achieved by adding the collisional excitation terms, k’CEnoΔne and kCEnone (kCE=rate constant for collisional excitation), to the numerator and denominator, respectively, of the second term of Eq. 9 above. By assuming dominance of collisional excitation, i.e.,
kCEnoΔne >> kC’ R(1)n+Δne , Eq. 10 is obtained. As the excitation energy is the same in the presence and absence of the interferent, Ea’= Ea , and ΔEa = 0 , i.e., dominance of electron collisional excitation would conform to LC 1A. Since of all systems studied in Table 4, none conform to LC 1A, we conclude that electron collisional excitation does not contribute significantly to the observed interference effects due to EIEs during ICP-AES and flame AES.
Simulation of Matrix Effects: Simplified Collisionalradiative Recombination Rate Model
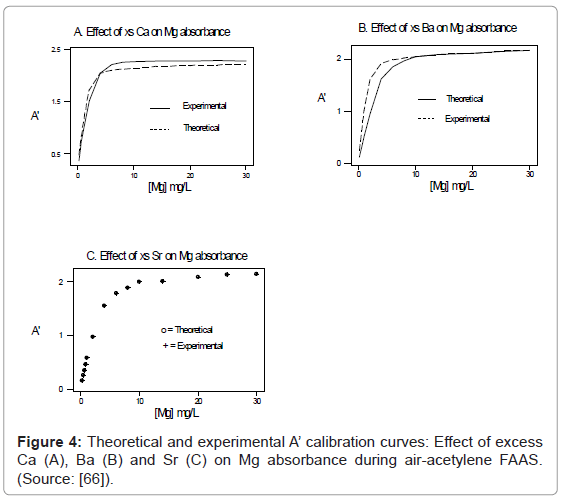
One of the major aims of plasma diagnostics is to be able to control the plasma for analytical purposes [1]. In this regard Zaranyika et al. [60] showed that combining Eq.4 and Eq. 10 above lead to Eqs. 18 and 19 which can be used to simulate the effects of interferents on analyte emission or absorbance calibration curve during atomic spectrometry,
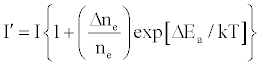 (18)
(18)
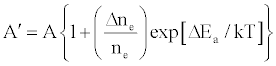 (19)
(19)
This was demonstrated when Eq. 19 was been used to simulate the Mg emission calibration curve when determined by flame AES in the presence of excess of Ca, Ba and Sr with very close agreement between theory and experiment, see Figure 4 [60]. Prediction of analyte calibration curve in the presence of interferents in terms of Eqs 4 and 10 should also be possible for ICP measurements, but has not been reported as yet. Prediction of analyte emission calibration curve in the presence of interferents suggests that complete prediction of analyte calibration curve in atomic optical spectrometry should be possible. To achieve this, ability to model analyte behavior in the absence of interferents is required. In addition to complete prediction of analyte calibration curve, further investigations of interference effects as a function of analyte and interferent ionization potential, and interferent concentration, are required in order to understand how different sample matrices affect different samples. Further work is also required to characterize interference effects as a function of plasma temperature and thus establish their spatial behavior. The emission correlation maps approach of Hieftje et al. [19] described above can be adapted for such studies.
Collisional-radiative Recombination Activation Energy: Implications with respect to filling of Atomic Orbitals
The discovery of the collisional radiative recombination activation energy during atomic spectrometry has necessitated the postulation of the existence of the ambipolar diffusion ion-electron pair. Figure 3 represents the emerging picture with regard to ionization and radiative recombination of ions and electrons in the plasma. Collisional radiative recombination is represented by Eq. 14 above. When applied to radiative recombination between the proton (or hydrogen ion) and an electron, Eq. 14 represents a model for the filling of atomic orbitals based on collisional radiative recombination. The model would have the advantage of taking into account the temperature dependence of the distribution of electrons among the various atomic orbitals as required by the Boltzmann law. This aspect is lacking in current theories of atomic structure, classical or quantum mechanical, and merits more attention. In saying this we recognize off-course that quantum mechanics cannot be equaled when it comes to probing the shapes of atomic and molecular orbitals.
Conclusion
In the early part paper we reviewed different approaches that are used to study matrix effects in the inductively coupled plasma. These include active spectroscopic methods, passive spectroscopic methods, classical rate models, and simplified rate models. Save for classical collisional-radiative rate models which have proved to be too complex to yield meaningful solutions, the other plasma diagnostic techniques are complementary in many respects. Active spectroscopic methods serve to characterize the plasma with respect to temperature and number density of electrons and atomic species, and have been able to demonstrate that the ICP is dominated by electrons from the ionization of argon. Passive spectroscopic methods serve to demonstrate the existence of matrix effects, especially those due to easily ionizable elements (EIEs). It is on the basis of active and passive spectroscopic methods that the conclusion that the ICP is not in thermal equilibrium was arrived at. Simplified rate models based on correlation maps of analyte emission and localized concentrations of analyte and interferent atomic species, is in fact a combination of active and passive spectroscopic methods, and serves to simultaneously characterize the plasma with respect to plasma temperature, number densities of electrons and atomic species, and the existence of matrix effects. Simplified rate models based on kinetic modeling of the signal enhancement ratio are designed to reveal the dominant excitation mechanism from the several mechanisms that have been proposed. This approach should allow prediction of the effects of interferents on analyte calibration curve, and hence allow corrections for any matrix effects observed in practice.
In the later part of the review, particular attention was focused on simplified rate models based on kinetic modeling of the signal enhancement ratio. From the detailed review given, it is apparent that through kinetic modeling techniques, considerable progress has been made towards elucidating the mechanisms leading to the interference effects observed when analytes are determined using ICP or flame atomic spectrometry in the presence of easily ionizable element interferents. The major excited-state populating process during ICP-AES and flame atomic spectrometry, is collisional radiative recombination. The departure of the flame or inductively coupled argon plasma from LTE is attributed to ambipolar diffusion whereby electrons exist in the plasma in both the ambipolar diffusion and LTE states simultaneously, depending on the composition, density, and temperature of the plasma. In the ambipolar diffusion state electrons exist as ionization limit ionelectron complexes, whose life-time appears to be an inverse function of plasma temperature and ionization potential of the parent atom or ion. In the ICP, electrons from the ionization of the analyte and Ar exist predominately in their ambipolar diffusion states, whereas electrons from the ionization of EIEs exist both in the LTE and ambipolar diffusion state. Because of the high ionization potential of Ar (15.755 eV), collisions involving electrons from the ionization of Ar in the ICP, are either elastic or do not lead to recombination, whereas collisions involving electrons from the ionization of EIE interferents can occur before or after thermal equilibration leading to the observed interference effects.
References
- Blades MW, Caughlin BL, Walker ZH, Burton LL (1987) Excitation, ionization and spectral line emission in the inductively coupled plasma. Prog Analyt Spectrosc 10: 57-109.
- De Galan L (1984) Some considerations on the excitation mechanism in the inductively coupled argon plasma. Spectrochim Acta Part B At Spectrosc 39: 537-550.
- Blades MW, Horlick G (1981) Interference from easily ionizable element matrices in inductively coupled plasma emission spectrometry-A spatial study. Spectrochim Acta Part B At Spectrosc 36: 881-900.
- Boumans PWJ (1966) Theory of Spectrochemical Excitations. Hilger and Watts, London.
- Howatson AM (1976) An Introduction to Gas Discharges. 2nd edition, Pergamon Press, Oxford.
- Hanselman DS, Sesi NN, Huang M, Hieftje GM (1994) The effect of sample matrix on electron density, electron temperature and gas temperature in the argon inductively coupled plasma examined by thomson and rayleigh scattering. Spectrochim Acta Part B At Spectrosc 49: 495-526.
- Herman R, Alkemade CTJ (1973) Chemical Analysis by Flame Photometry.Interscience Publishers, New York, pp 311-318.
- Todoli JL, Gras L, Hermandis V, Mora J (2002) Elemental matrix effects in ICP-AES: A Review. J Anal At Spectrom 17: 142-169.
- Boumans PWJM (1987) Inductively Coupled Plasma Emission Spectroscopy: Methodology, instrumentation, and performance. Part III, Wiley Interscience, NY, 387.
- Boumanns PWJM (1987) Inductively Coupled Plasma Emission Spectroscopy Part I. John Wiley, New York.
- Hasegawa T, Haraguchi H (1985) Appreciation of a collisional-radiative model for the description of an inductively coupled argon plasma. Spectrochim Acta Part B At Spectrosc 40: 1067- 1084.
- Fujimoto T (1979) Kinetics of ionization-recombination of a plasma and population density of excited ions. I. equilibrium plasma. J Phys Soc Jpn 47: 265-272.
- Desai SV, Corcoran WH (1969) Recombination of electrons and ions in an atmospheric argon plasma. J Quantitative Spectroscopy and Radiation Transfer 9: 1371-1386.
- Vicek J, Pelikan V (1992) Collisional-radiative ionization and recombination in an inductively coupled argon plasma. Spectrochim Acta Part B At Spectrosc 47: 681-688.
- Goldwasser A, Mermert JM (1986) Contribution of the charge-transfer process to the excitation mechanism in inductively coupled plasma atomic emission spectrometry. Spectrochim Acta Part B At Spectrosc 41: 725-739.
- Van der Mullen JAM, Raaijmakers IJMM, van Lammeren ACAP, Schram DC, van der Sijde B, et al. (1987) On the charge transfer in an ICAP. Spectrochim Acta Part B At Spectrosc 42: 1039-1051.
- Chan GCY, Hieftje GM (2004) Using matrix effects as a probe for the study of the charge-transfer Mechanism in inductively coupled plasma-atomic emission spectrometry. Spectrochim Acta Part B At Spectrosc 59: 163-183.
- Hieftje GM (1992) Plasma diagnostic techniques for understanding and control. Spectrochim Acta Part B At Spectrosc 47: 3-25.
- Hieftje G, Huang M, Lehn S, Warner K, Gamez G, et al. (2002) Toward a fuller understanding of analytical atomic spectrometry. Anal Sci 18: 1185-1189.
- Hori T, Kogano M, Bowden MD, Uchino K, Muraoka K (1998) A study of electron energy distribution in an inductively coupled plasma by laser thomson scattering. J Appl Phys 83: 1909-1916.
- Marshall KA, Hieftje GM (1988) Thomson Scattering for determining electron concentrations and temperatures in an ICP - I. assessment of the technique for a low-flow, low-power plasma. Spectrochim Acta Part B At Spectrosc 43: 841-849.
- Huang M, Hieftje GM (1985) Thomson scattering from an ICP. Spectrochim Acta Part B At Spectrosc 40: 1387-1400.
- Marshall KA, Hieftje GM (1988) Thomson scattering for determining electron concentrations and Temperatures in an ICP- II. Description and evaluation of a multichannel instrument. Spectrochim Acta Part B At Spectrosc 43: 851-865.
- Huang M, Marshall KA, Hieftje GM (1986) Electron temperatures and electron number densities measured by thomson scattering in the inductively coupled plasma. Anal Chem 58: 207-210.
- Huang M, Hieftje GM (1989) a new procedure for determination of electron temperatures and electron concentrations by thomson scattering from analytical plasmas. Spectrochim Acta Part B At Spectrosc 44: 291-305.
- Monnig CA, Marshall KA, Rayson GD, Hieftje GM (1988) Tomographic image reconstruction techniques for spectroscopic sources: 1. Theory and computer simulations. Spectrochim Acta Part B At Spectrosc 43: 1217-1233.
- Monnig CA, Gebhart BD, Marshall KA, Hieftje GM (1990) Tomographic image reconstruction techniques for spectroscopic sources: ii. instrumentation. Spectrochim Acta Part B At Spectrosc 45: 261-270.
- Sesi NN, Hanselman DS, Galley P, Horner J, Huang M, et al. (1997) An imaging-based instrument for fundamental plasma studies. Spectrochim Acta Part B At Spectrosc 52: 83-102.
- de Olivares DR, Hieftje GM (1981) Saturation of energy levels in analytical atomic fluorescence Spectrometry - II experimental. Spectrochim Acta Part B At Spectrosc 36: 1059-1079.
- Olivares DR, Hieftje GM (1978) Saturation of energy levels in analytical atomic fluorescence spectrometry - I. theory. Spectrochim Acta Part B At Spectrosc 33: 79-99.
- De Regt JM, de Groote FPJ, van der Mullen JAM, Schram DC (1996) Comparison of active and passive spectroscopic methods to investigate atmospheric inductively coupled plasmas. Spectrochim Acta Part B At Spectrosc 51: 1371-1383.
- Tripkovic MR, Holclajtner-Antunovic ID (1993) Study of matrix effect of easily and non-easily ionizable elements in an inductively coupled plasma - Part I. Spectroscopic diagnostics. J Anal At. Spectrom 8: 349-357.
- Holclajtner-Antunovic ID, Tripkovic MR (1993) Study of matrix effect of easily and non-easily ionizable elements in an inductively coupled plasma-Part 2 Equilibrium plasma composition. J Anal At Spectrosc 8: 359-365.
- Galley PJ, Glick M, Hieftje GM (1993) Easily ionizable element interferences in inductively coupled plasma atomic emission spectroscopy - I. effect on radial analyte emission patterns. Spectrochim Acta Part B At Spectrosc 48: 769-788.
- Lazar AC, Farnsworth (1999) Matrix effect studies in the inductively coupled plasma with monodisperse droplets - Part 1. The influence of matrix on the vertical analyte emission profile. Appl Spectrosc 53: 457-464.
- Furuta N, Horlick G (1982) Spatial characterization of analyte emission and excitation temperature in an inductively coupled plasma. Spectrochim Acta Part B At Spectrosc 37: 53-64.
- Kitagawa K, Horlick G (1992) Deviation of level population of iron atoms and ions from the Boltzmann distribution in an inductively coupled plasma. J Anal At Spectrosc 7: 1221-1229.
- Vander Mullen JAM, Nowak S, van Lammeren ACAP, Schram DC, van der Sijde B (1988) Non-equilibrium characterization and spectroscopic analysis of an inductively coupled argon plasma. Spectrochim Acta Part B At Spectrosc 43: 317-324.
- Morel V, Bultel A, Cheron BG (2010) Modelling of thermal and chemical non-equilibrium in a laser-induced aluminium plasma by means of a collisional-radiative model. Spectrochim Acta Part B At Spectrosc 65: 830-841.
- Burm KTAL (2004) Deviations from thermal equilibrium in plasmas. Phys Lett A 328: 489-492.
- Leornard SL (1972). Evidence for departure from equilibrium in a RF induction plasma in atmospheric-pressure argon. J Quantitative Spectroscopy and Radiation Transfer 12: 619-626.
- Fujimoto T (1979) Kinetics of ionization-recombination of a plasma and population density of excited ions. II. ionizing plasma. J Phys Soc Jpn 47: 273-281.
- Fujimoto T (1980) Kinetics of ionization-recombination of a plasma and population density of excited ions. IV. recombining plasma- high temperature case. J Phys Soc Jpa 49: 1561-1568.
- Bates DR, Kingston AE, McWhirter RWP (1962) Recombination between electrons and atomic ions. II. Optically thick plasmas. Proc Roy Soc Lond A 13 270: 155-167.
- Bates DR, Kingston AE (1964) Collisional-radiative recombination at low temperatures and densities. Proc Phys Soc 83: 43-48.
- McWhirter RWP, Hearn AG (1963) A calculation of the instantaneous population densities of the excited levels of hydrogen-like ions in a plasma. Proc Phys Soc 82: 641-654.
- McWhirter RWP (1965) Spectral Intensities. Chapter 5, In: Plasma Diagnostic Techniques, Huddlestone RH, Leornard SL (eds), Academic Press, New York, 201-264.
- Lovett RJ (1982) A rate model of inductively coupled argon plasma analyte spectra. Spectrochim Acta Part B At Spectrosc 37: 969-985.
- HasegawaT, Haraguchi H (1985) A collisional-radiative model including radiation trapping and transport phenomena for diagnostics of an inductively coupled argon plasma. Spectrochim Acta Part B At Spectrosc 40: 1505-1515.
- Hieftje GM, Rayson GD, Olesik JW (1985) A steady-state approach to excitation mechanisms in the ICP. Spectrochim Acta Part B At Spectrosc 40: 167-176.
- Rayson GD, Hieftje GM (1986) A steady-state approach to evaluation of proposed excitation mechanisms in the analytical ICP. Spectrochim Acta Part B At Spectrosc 41: 683-697.
- Hieftje GM, Wu M (1994) The effect of easily ionized elements on analyte emission efficiency in Inductively coupled plasma spectrometry. Spectrochim Acta Part B At Spectrosc 49: 149-161.
- Hieftje GM, Lehn SA (2003) Experimental evaluation of analyte excitation mechanisms in the inductively coupled plasma. Spectrochim Acta Part B At Spectrosc 58: 1821-1836.
- Zaranyika MF, Nyakonda C, Moses P (1991) Effect of excess sodium on the excitation of potassium in an air-acetylene flame: A steady state kinetic model which takes into account collisional excitation. Fresenius J Anal Chem 341: 577-585.
- Zaranyika MF, Makuhunga P (1997) A possible steady state kinetic model for the atomization process during flame atomic spectrometry: application to mutual atomization interference effects between group I elements. Fresenius J Anal Chem 357: 249-257.
- Zaranyika MF, Chirenje AT (2000) A possible steady state kinetic model for the atomization and excitation processes during inductively coupled plasma atomic emission spectrometry: Application to study of interference effects of lithium on calcium. Fresenius J Anal Chem 368: 45-51.
- Zaranyika MF, Chirenje AT, Mahamadi C (2007) Interference effects from easily ionizable elements in Flame AES and ICP-OES: A proposed simplified rate model based on collisionl charge transfer between analyte and interferent species. Spectrosc Lett 40: 835-850.
- Zaranyika MF, Chirenje AT, Mahamadi C (2012) Interference effects of easily ionizable elements in ICP-AES and flame AAS: characterization in terms of the collisional radiative recombination activation energy. Spectrosc Lett 45: 1-12.
- Zaranyika MF, Mahamadi C (2013) Departure from local thermal equilibrium during inductively coupled plasma atomic emission spectrometry: characterization in terms of collisional radiative recombination activation energy. Pure Appl Chem ASAP article
- Zaranyika MF, Chirenje AT, Mahamadi C (2012) Interference effects of excess Ca, Ba and Sr on Mg absorbance during flame atomic absorption spectrometry: Characterization in terms of a simplified collisional rate model. Atomic Absorption Spectroscopy, InTech Publishers, Croatia, 131-142.
- Allen CW (1955) Astrophysical quantities. Athlone Press, London, UK.
- Willard HH, Merritt LL, Dean JA, Dean Jr FA (1988) Instrumental methods of analysis. 7th edition, Wadsworth, London.
- Pupyshev AA, Semenova EV (2001) Formation of doubly charged atomic ions in the inductively coupled plasma. Spectrochim Acta Part B At Spectrosc 56: 2397-2418.
- Lide DR (1992) Handbook of Chemistry and Physics 73rd edition. CRC Press, London, 10-211.
Relevant Topics
Recommended Journals
Article Tools
Article Usage
- Total views: 15479
- [From(publication date):
November-2013 - Dec 20, 2025] - Breakdown by view type
- HTML page views : 10731
- PDF downloads : 4748