Research Article Open Access
Spatial Modelling of the Variability of the Soil Moisture Regime at the Landscape Scale in the Southern Qilian Mountains, China
CY Zhao1*, SZ Peng1 and ZD Feng2
1Key laboratory of arid and grassland agroecology (Ministry of Education), Lanzhou University, Lanzhou 730000, China
2Key laboratory of western China’s environment systems (Ministry of Education),Lanzhou University, Lanzhou 730000, China
- *Corresponding Author:
- CY Zhao
Key Laboratory Of Arid And Grassland Agroecology (Ministry of Education)
Lanzhou University, Lanzhou 730000
E-mail: nanzhr@lzb.ac.cn
Received Date: October 26, 2010; Accepted Date: March 03, 2011; Published Date: March 05, 2011
Citation: Zhao CY, Peng SZ, Feng ZD (2011) Spatial Modelling of the Variability of The Soil Moisture Regime At The Landscape Scale In The Southern Qilian Mountains, China. J Ecosys Ecograph 1:102. doi:10.4172/2157-7625.1000102
Copyright: © 2011 Sethy NK, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and and source are credited.
Visit for more related articles at Journal of Ecosystem & Ecography
Abstract
The spatial and temporal variability of the soil moisture status gives an important base for the assessment of ecological (for forest restoration) and economic (for agriculture) conditions at micro- and meso-scales. It is also an essential input into many distributed hydrological models. However, there has been a lack of effective methods for its estimation at the landscape scale in the study area. The objective of this study is to model the variability of the soil moisture regime in the southern Qilian Mountains with an area of 10,009 km 2 . First, a small catchment named Pailugou catchment (area of 10 km 2 ) is selected. A modified wetness index, including the topographic wetness index, solar radiation and the monthly mean precipitation, is developed. Based on GIS-assisted regionalization of parameters, the soil moisture status at the grid scale of 1×1 m 2 can be estimated using the modified wetness index in Pailugou catchment. Secondly, we validate the method with a collection of 15 points within the small catchment. The results show that soil moisture status estimations are significantly improved of using the modified wetness index. 77% of the spatial variability of soil moisture can be explained by the index in Pailugou catchment. That assures our confidence in the modified wetness index to estimate the soil moisture status. Finally, the method is applied to the southern Qilian Mountainous regions, northwestern China. At the landscape scale, the parameters needed by the index are regionalized. For instance, the temporal-spatial distribution of monthly mean precipitation is simulated by the linear regression model. The slope and special upslope area are extracted from the DEM of southern Qilian Mountains with a 10 m resolution. Based on the modified wetness index, the variability of the soil moisture regime in the region has been simulated. From the study, the conclusion can be drawn that: ①the soil moisture status shows higher at the gentle bases of long hill-slopes than at the steep short sites, higher in the north-facing slope than in the south-facing slope. ② the driest sites occurred on some ridges in the northern part and the western part of the study area, the wettest sites were registered in the low valleys of the Heihe River and its major tributaries in the eastern part. Comparing the spatial distribution pattern of vegetation with that of soil moisture status modeled in the study area, we found the spatial distribution pattern of vegetation has nearly relative with that of soil moisture status.
Keywords
Soil moisture status; Precipitation; Linear regression; A modified wetness index; Qilian mountains
Introduction
The Heihe River Basin, the second largest inland river basin in the arid regions of northwestern China, consists of three major geomorphic units: the southern Qilian Mountains area, the middle Hexi Corridor, and the northern Alxa Highland. The southern Qilian Mountains area is hydrologically and ecologically the most important unit because of the function as the water source to support the irrigating agriculture in the Hexi Corridor and also to maintain the ecological viability in the northern Alxa Highland. With the rapid growth of population, agricultural irrigation areas increasingly spread in the middle Hexi Corridor. As a result, the already-existing conflict between agricultural use of the water here and ecological demand of the water in the Alxa Highland has recently been exacerbated. How to resolve the conflict and coordinate the development in economy and ecological environments becomes the focus of attention in the Heihe River basin. Many researchers have dealt with water resources carry capacity [1], ecological requirement water [2,3], methods of irrigation and so on. However, the runoff amount of the Heihe River and its variation should be paid more attention [4]. Because the runoff from the southern Qilian Mountains approximately represents the total water resources amount of the middle Hexi Corridor and the northern Alxa Highland. Therefore, accurate estimation of runoff from Qilian Mountainous area is an urgent need for evaluating Heihe River water resources carry capacity and for water management and planning. To accomplish the needed runoff estimation in the upper reaches, several distributed hydrological models have been applied for the practical purpose. But one of the most problems to run distributed hydrological models is regionalization of soil moisture. It thus has to be spatially and temporally portrayed [5-8]. For this reason, during the last 30 years there have been various studies that have attempted to develop methods to estimate the soil water content over a large region [9-12]. The one commonly used is extrapolation approach by point measurements extrapolated across the landscape with geostatistical techniques [13-15]. Unfortunately, point measurements by groundbased methods (e.g. neutron thermalization, oven-dry method) are much too labor-intensive to be applied for a large area (e.g., in the entire southern Qilian Mountains). Another common method is to use models to estimate soil moisture, for example, wetness index model [16-19]. The wetness index model hypothesizes that the spatial distribution of topographic attributes that characterize these flow paths inherently captures the spatial variability of soil moisture status at the meso-scale. However, at the micro-scale, soil moisture patterns are influenced by a number of factors such as soil properties, vegetation, and climatic conditions besides topographic attributes [20-22]. Climate probably exerts the control role in heterogeneity of soil moisture at the micro-scale level [23,24]. Thus, in this study the relationship between soil moisture and its impact factors (e.g. topography, solar radiation and precipitation) is established. Topographic attributes and solar radiation can be easily calculated from a digital elevation model (DEM). Whereas, precipitation fields on a regular grid and in digital forms must be inferred from neighbouring meteorological stations or from relationships with other variables [25]. There are many methods of interpolating precipitation from monitoring stations to grid points [26-30]. Basic techniques such as Kriging, Spline, Inverse Distance Weighted use only the geographic coordinates of the sampling points and the value of the measured variable. In addition, regression models are using only additional information as regression relationships between precipitation and various topographic variables such as altitude, latitude, continentality, slope, orientation or exposure [31- 35]. But few researchers could interpolate precipitation by regression models in the study area because of unavailable digital elevation models (DEM). Fortunately, significant progress in this area has recently been achieved through the development of DEM with a resolution of 10m by the remote sensing laboratory of Cold and Arid Regions Environmental and Engineering Research Institute, CAS. The topographic factors can be best delineated by the DEM datum.
This study develops a modified wetness index in order to map the soil moisture status across the southern Qilian Mountains. In the following sections we will present the various steps that lead to the mapping of the soil moisture regime: (1) use of the modified wetness index in Pailugou catchment; (2) validation of the results by the available data; (3) Regionalization of parameters included in the modified wetness index; and finally (4) mapping of the soil moisture status distribution in the southern Qilian Mountains.
Materials and Methods
Study area
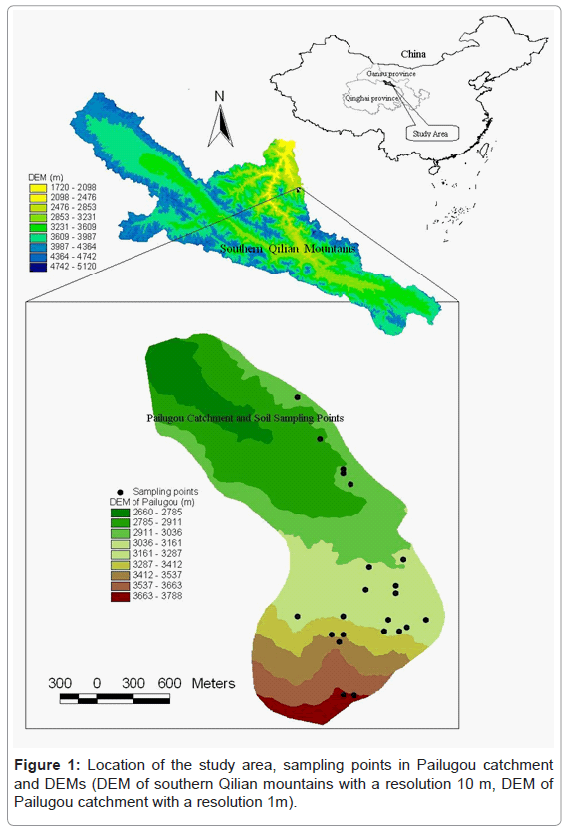
The study area, one portion of the Qilian Mountains within the Heihe River Basin, is located between 98º34'- 101º11' E and 37º41'- 39°05' N and covers an area of approximately 10, 009km2, with the elevation ranging from 2000 to 5500 m a.s.l. Administratively, the major part of the study area is in Gansu Province and a small part in Qinghai Province (Figure 1). The annual mean precipitation increases with the increasing elevation (from 250-700mm). The inter-annual variability in the precipitation for the period 1957-1995 is as high as 80%, and over 88% of the precipitation falls between May and September. Figure 2 shows the pattern of rainfall over the year in Zhamashike meteorological station (one representative meteorological station in the study area). The annual mean temperature decreases with the increasing elevation (from 6.2-9.6°C). The vegetation distribution closely follows the combinations of temperature and precipitation in the Mountains. They are (from low to high elevations): desert steppe, forest steppe, sub-alpine shrubby meadow, alpine cold desert, and ice/snow zone. Desert steppe, ranging from 2100m to 2500m a.s.l., is made up of Stipa breviflora and Stipa bungeana with low coverage. Forest steppe, occupying altitude space from 2500m to 3400m a.s.l., is composed of forests in shady slopes and the steppe in sunny slopes. The forests is dominated by Qinghai spruce (Picea crassifolia) with Qilian Cypress (Sabina przewalskii), shrubs(e.g., Dasiphora fruticosa, Caragana jubata) and the steppe dominated by Stipa purpurea, Stipa przewalskii, Carex kansuensis. Sub-alpine shrubby meadow, being from 3400m to 4000m a.s.l., covered by Salix gilasnanica and Kobresia tibetica with highest coverage. Alpine cold desert and ice/ snow zones are located above 4000m a.s.l. In addition to the obvious vertical zonality, horizontal zonality also exits due to precipitation and air temperature differences from the south to the north and from the east to the west. Generally, precipitation decreases from the east to the west and increases from the north to the south but the temperature is reverse in the study area.
Data collection
The monthly mean precipitation data (from 1957-1995) were obtained from 43 rain-gauge stations located within the study area and the surrounding areas. The locations and the altitudes of these stations were measured with a global positioning system (GPS) and an elevation meter. Among 43 rain-gauge stations, 30 stations were chosen to develop the regression model or to use for interpolating and other 13 stations were remained to test the regression model or the results of interpolation. Total 22 plots were located to measure soil water content in Pailugou catchment (one representative comprehensive research catchment in the study area located at 38.55°N, 100.30°E) (Figure 1). Pailugou catchment covers an area of 10km2, with the elevation ranging from 2600m to 3800m a.s.l. Soil was sampled on a biweekly interval at four depths (0-10, 10-20, 20-40, 40-60cm) from May to September in 2003 and 2004. If rainfall occurs, observation will be subjoined after precipitation event. Soil water content (SWC) was measured by the conventional oven-dry method. Calculation of mean value of SWC is demonstrated as follows: suppose that SWC of plot i, layer j, sampling occasion k is expressed as SWCi,j,k. Nj represents the number of sampling soil layer or soil depths and is 4 in this study; Nk is the number of sampling occasion in each month, which minimum is 2. Mean SWC in each month on plot i (SWCi) is calculated as follows:
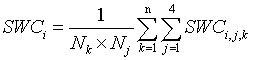 (1)
(1)
At final, we can get available data of 15 plots, which was used to validate the model mentioned hereinafter. Pailugou catchment has a weather station at the catchment outlet. 16 rain gauges were located along elevation gradient, on a 100m interval between 2600-3500m and on 50m intervals between 3500-3800m, for providing information on the spatial variability of rainfall.
Present distribution map of vegetation types was from Bureau of Qilian Mountains National Nature Reserve in Gansu province.
Description of models
Hydrological modelling at the micro- and meso-scales is related to the ability to characterize the spatial variability of the soil water content. However, soil moisture characterized by temporal and spatial variations even in a small catchment. In mountainous terrains, the soil water distribution is controlled by vertical and horizontal water divergence and convergence, infiltration recharge, and evapotranspiration. The latter two terms are affected by solar insolation and the vegetation canopy that vary strongly with exposure in arid areas. The divergence/ convergence term is dependent on hill-slope position [36]. Considering the hill-slope position, most index approaches for predicting the spatial distribution of soil water can be expressed as [16]:
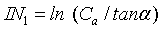 (2)
(2)
where IN1 is the wetness index, Ca is the contributing area named the upslope area per unit contour length, is also called special upslope area and computed as Ca=A/L, where A (m2) is the upslope area and L (m) is the contour length, α is the local slope of the terrain defined as the ratio of the altitude change to the horizontal distance between any two points on the hillside. The soil water content is not only affected by the divergence/convergence of water but also affected by evapotranspiration. For mountainous region in arid areas, evapotranspiration is obviously different in different aspects because of variations of insolation. So Equation (2) has been modified by merely introducing the factor of solar radiation (SR). Generally, south facing sites get more insolation than north facing sites. Soil moisture at south facing sites is thus lower than that at north facing sites due to dryness of insolation. For calculating expediently, aspect was used for an appropriate surrogate of potential insolation [23,37]. However, it is difficult to quantify soil moisture status by aspect. Here, we calculated the spatial distribution of SR in different month taking topographical attributes such as aspect, slope and time into consideration, the solar radiation is calculated as follows:
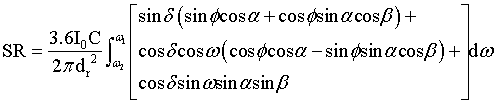 (3)
(3)
where, I0 is sun constant (0.08208 MJ m-2), C is the transform coefficient from day to minute and is 1440 min, dr is the relative distance between the earth and the sun and 1 0.033cos(2 / 365 ) r d = + π × J , J is the Julian day number, φ is the latitude, α is the local slope of the terrain, β is the aspect, δ is the solar declination (in radians) and δ = 0.4093sin(2π / 365× J -1.405) , ω is the hour angle (in radians) and ω=arcos(-tanφtanδ). With the ArcGIS (9.2 version), solar radiation (SR) fields on a regular grid and in digital forms can be easily calculated by using DEM and time. The time step was selected as 30 minute. The wetness index IN1 has been changed by introducing SR. Then, the Equation (2) becomes:
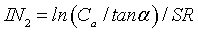 (4)
(4)
The soil moisture at landscape scales has closely related to the spatial distributions of precipitation. Equation (4) has been modified by introducing the factor of precipitation [38] and given as the following:
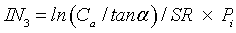 (5)
(5)
where IN3 is a modified soil wetness index in every month, Pi is the monthly mean precipitation. Equation (5) requires four parameters: the local slope of the terrain (α), solar radiation (SR), the contributing area (Ca) and precipitation (Pi). α and Ca can be computed from DEM.
According to 16 rain gauges located in Pailugou catchment, regression relationship between the monthly mean rainfall and altitude is built, which is presented as:
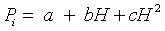 (6)
(6)
where H is the altitude in meter, a, b and c are the regression coefficients (Table 1). The temporal and spatial distributions of precipitation in Pailugou catchment were simulated by the regression model.
| time | a | b | c | R2 |
| Apr. | -194.41 | 0.1344 | -0.000021 | 0.965 |
| May | -345.24 | 0.2386 | -0.000037 | 0.969 |
| Jun. | -1411.6 | 0.9756 | -0.000151 | 0.968 |
| Jul. | -1120.7 | 0.7745 | -0.000120 | 0.968 |
| Aug. | -504.77 | 0.3489 | -0.000054 | 0.967 |
| Sep. | -545.41 | 0.3770 | -0.000059 | 0.967 |
Table 1: Monthly regression coefficients and R2 needed to calculate monthly mean precipitation using altitude (H) for Pailugou catchment (P = a + bH+cH2).
At micro-scale, we here used five methods to simulate the temporal and spatial distribution of precipitation in the southern Qilian Mountains, i.e. linear regression, inverse distance weighted (IDW), ordinary kriging (OK), trend and spline. The regression model derived by regression analyses can predict annual, monthly precipitation as functions of elevation and geographical coordinates [30,39]. By the analysis of the precipitation data with their elevation and geographical coordinates in the study, a linear regression relationship between the monthly mean rainfall and locational/topographic factors is presented as:
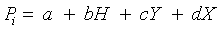 (7)
(7)
where H is the altitude in meter, Y is the latitude in degree, X is the longitude in degree and a, b, c, d are the regression coefficients (Table 2).
| time | a | b | c | d | R2 |
| Jan. | -19.811 | 0.000260 | -0.051 | 0.231 | 0.207 |
| Feb. | -70.701 | 0.001103 | 0.221 | 0.626 | 0.331 |
| Mar. | -249.545 | 0.003390 | 0.433 | 2.336 | 0.406 |
| Apr. | -16.862 | 0.004009 | -4.289 | 1.879 | 0.584 |
| May | 408.331 | 0.009569 | -12.540 | 0.869 | 0.810 |
| Jun. | 530.716 | 0.021000 | -13.656 | 0.016 | 0.863 |
| Jul. | 689.699 | 0.029650 | -12.485 | 1.018 | 0.870 |
| Aug. | 495.902 | 0.018520 | -19.839 | 2.869 | 0.879 |
| Sep. | 196.940 | 0.009100 | -15.049 | 4.003 | 0.856 |
| Oct. | -5.170 | 0.002153 | -5.737 | 2.341 | 0.841 |
| Nov. | -136.015 | 0.000984 | 0.240 | 1.283 | 0.455 |
| Dec. | -81.180 | 0.000480 | 0.493 | 0.627 | 0.166 |
| Annual | 1742.001 | 0.097260 | -87.915 | 17.197 | 0.861 |
Table 2: Monthly linear regression coefficients and R2 needed to calculate monthly mean precipitation using altitude (H), latitude (Y) and longitude (X) for the southern Qilian Mountains (P = a + bH + cY + dX).
Besides the regression model, four conventional interpolation methods, inverse distance weighted (IDW), spline, ordinary kriging (OK), and trend, were tested. IDW estimates the value of an unsampled area as a weighted average of a defined number of neighborhood points, or area, and the weight assigned to each neighborhood point diminishes as the distance to the neighborhood point increases [40]. Spline interpolators have been widely used in developing climatic surfaces from sparse observation points [41]. The interpolated surface based on spline (a) passes exactly through the data points and (b) has a minimum curvature. OK is a geostatistical procedure that uses a variogram model, which describes the spatial continuity of the input data to estimate values at unsampled locations [42]. The variability between samples as a function of distance (i.e., semivariance) is evaluated and modeled prior to kriging [43]. The trend surface interpolator uses a polynomial regression to fit a least-squares surface to the input points. It creates smooth surfaces. The surface generated will seldom pass through the original data points since it performs the best fit for the entire surface.
Results and Discussion
Wetness indexes
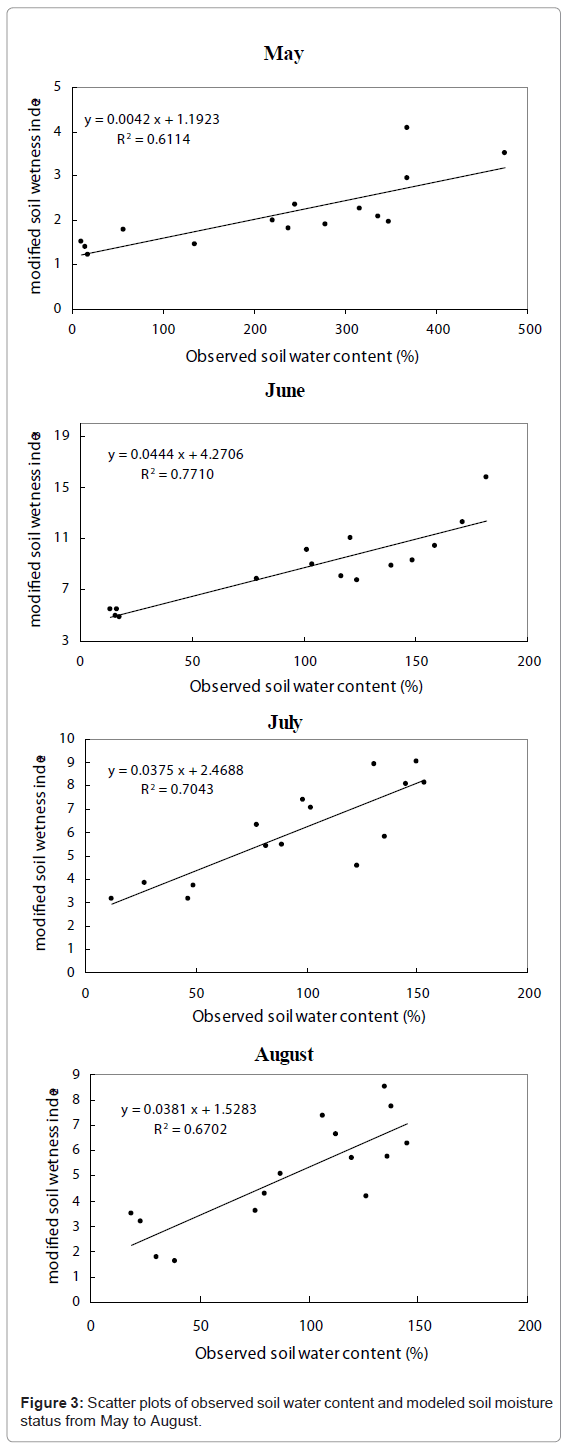
The parameters, such as slope, solar radiation and the contributing area were computed from the DEM of Pailugou catchment. The spatial distribution of precipitation was obtained by Equation (6) and the unit of precipitation was transformed into energy unit by multiplying the coefficient of latent heat of vaporization (2.45MJ kg-1). The maps of the wetness index (IN1 and IN2) and the modified wetness index (IN3.) in Pailugou catchment were obtained from the models using Grid module in ARC/INFO software. The simulated wetness indexes were validated by observed data. We found that IN1 was able to explain between 34% and 38% of the spatial variability of soil moisture based on the observation of SWC. If the solar radiation was considered as a complementary factor (IN2), the capacity to explain the spatial variability of soil moisture increased up to 45%-70.2%. However, Equation (2) and Equation (4) only take the topographic factors into account. If spatially inhomogeneous precipitation is considered as another complementary factor (i.e. Equation (5)), the capacity to explain the spatial variability of soil moisture can reach 61.1%-77.1% in Pailugou catchment (Figure 3). According to investigation of 16 raingauges in Pailugou catchment, the mean increase rate of precipitation is 35mm/100m. Precipitation reaches the maximum value at the altitude 3400m. From 2600 to 3000m, the soil covered 10-15cm depth of litter and semi-decomposed organic layer and has 20-30cm depth of humus layer. The two layers have high water holding capacity, which can intercept most of throughfall precipitation and store the water in the soil. If contributing area and slope are only considered (e.g. Equation (2)), the soil wetness index should decrease gradually with increase of altitude due to contributing area decrease and steep slope increase. But, at fact, soil moisture observed is increase with altitude increase because of precipitation increase and high soil water holding capacity. So precipitation introduced into the wetness index model can improve the accuracy of soil moisture simulation.
Spatial and temporal distributions of precipitation
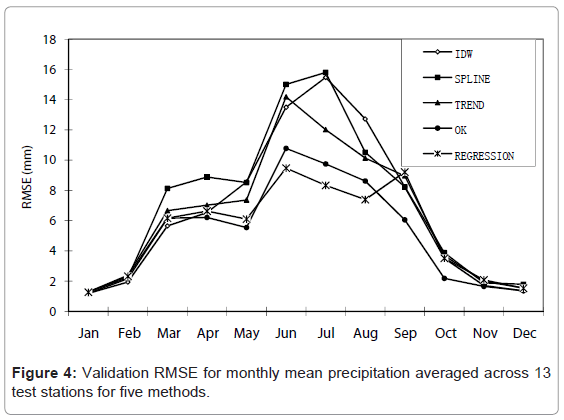
Prediction of precipitation on the locations of the validation points and the measured values at these locations were compared by three criteria: the mean error (ME), the mean absolute error (MAE) and the root mean square error (RMSE). ME indicates the degree of bias, MAE provides a measure of how far the estimate can be in error, ignoring the sign, and RMSE provides a measure that is sensitive to outliers. A summary of the errors obtained from the criteria was presented in Table 3. ME was relatively low for IDW, OK, trend and linear regression model (Equation (7)), but was generally lowest for the linear regression model. The linear regression and OK methods gave the lower MAE and RMSE. The spline gave consistently poor performances. For five methods, there were substantial variations in RMSE through the year (Figure 4). The highest errors occurred from July to September and the lowest values from October to February, which probably reflected the greater precipitation differences across the region in summer. From June to August, the linear regression model (Equation (7)) performed better than OK. Thus the conclusions are as follows: on average over the year, larger predictions errors were obtained by the spline, the trend and IDW methods that ignore elevation factors, with the worst results produced by the spline. It was noteworthy that for several months (from January to May, from September to December), OK yielded smaller prediction errors than the linear regression of precipitation against elevation and locational/topographic factors.
| Models | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | |
| ME | IDW | 0.20 | 0.95 | 2.56 | 0.83 | -1.2 | 5.97 | -2.58 | 1.28 | -4.56 | 0.3 | -0.68 | 0.59 |
| TREND | 0.31 | 0.72 | 1.32 | 5.33 | 0.40 | 0.64 | 0.31 | 0.72 | 1.32 | 5.33 | 0.40 | 0.64 | |
| OK | 0.22 | 0.97 | 2.54 | 1.48 | 0.35 | 6.73 | -2.23 | 2.66 | -3.78 | 0.75 | -0.65 | 0.58 | |
| SPLINE | 0.42 | 1.16 | 3.65 | 2.59 | 1.27 | 9.98 | -0.94 | 4.5 | -3.3 | 1.02 | -0.38 | 0.7 | |
| REGRESSION | 0.32 | 1.04 | 2.3 | 0.36 | -1.51 | 6.15 | -3.56 | -0.23 | -6.09 | -0.57 | -0.75 | 0.7 | |
| MAE | IDW | 0.84 | 1.56 | 4.46 | 5.34 | 6.84 | 11.41 | 12.68 | 9.98 | 6.47 | 3.1 | 1.52 | 1.15 |
| TREND | 1.06 | 2.09 | 5.24 | 6.10 | 6.34 | 11.89 | 10.93 | 8.44 | 7.53 | 3.17 | 1.67 | 1.33 | |
| OK | 0.84 | 1.89 | 5 | 4.85 | 4.57 | 8.15 | 8.18 | 7.06 | 4.8 | 1.63 | 1.41 | 1.18 | |
| SPLINE | 0.97 | 1.81 | 7.29 | 6.99 | 7.04 | 12.18 | 12.57 | 9.71 | 6.68 | 2.79 | 1.51 | 1.47 | |
| REGRESSION | 1.05 | 1.98 | 4.94 | 5.86 | 5.03 | 7.46 | 6.07 | 4.6 | 7.41 | 2.92 | 1.72 | 1.3 | |
| RMSE | IDW | 1.19 | 1.94 | 5.65 | 6.53 | 8.56 | 13.50 | 15.47 | 12.72 | 8.23 | 3.51 | 1.71 | 1.35 |
| TREND | 1.28 | 2.22 | 8.13 | 8.88 | 8.52 | 15.01 | 15.80 | 10.52 | 8.23 | 3.88 | 1.88 | 1.79 | |
| OK | 1.18 | 2.16 | 6.16 | 6.21 | 5.54 | 10.78 | 9.75 | 8.62 | 6.05 | 2.18 | 1.65 | 1.37 | |
| SPLINE | 2.22 | 8.13 | 8.88 | 8.52 | 15.01 | 15.80 | 10.52 | 8.23 | 3.88 | 1.88 | 1.79 | 2.22 | |
| REGRESSION | 1.27 | 2.32 | 6.16 | 6.63 | 6.10 | 9.47 | 8.33 | 7.39 | 9.21 | 3.51 | 2.08 | 1.53 |
Table 3: Validation errors averaged across 13 test sites for the five interpolation methods in each month.
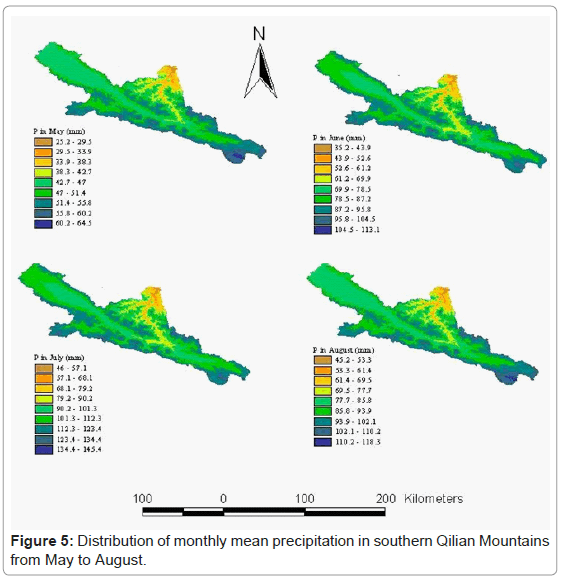
As mentioned above, over 88% of the precipitation falls between May and September and over 63% between June and August in the southern Qilian Mountainous areas of the Heihe River Basin. We were here focusing on the spatial distribution of precipitation during the ecologically meaningful time period, i.e., growing seasons approximately from May to August. Our comparison between these models' performances demonstrated that the linear regression model (Equation (7)) did the best job during the ecologically meaningful time period. The best performance of the linear regression in the study area made this model (Equation (7)) the best choice. A series of spatialdistribution maps of precipitation were obtained by the regression model (Figure 5). Figure 5 showed that lower precipitation values were registered in the low valleys of the Heihe River and the northwest part, and higher precipitation values appeared in the areas with higher altitude and southeast part. Figure 5 also showed that precipitation value had temporal variations during growing seasons (i.e. from May to August), highest precipitation value, ranging from 46mm to 145.4mm, appearing in the July, and the lowest precipitation value, from 25.2mm to 64.5mm, being seen in May.
Temporal and spatial distribution of soil moisture status in the southern qilian mountains
The soil moisture data are fairly sparse in the study area. We could not collect the soil moisture data except in Pailugou catchment. The soil moisture status of Pailugou catchment was simulated using Equation (5). To test the spatially-modeled results of the soil moisture status in the catchment, we compared the observed results for 4 months at 15 sample plots with the spatially-modeled results for the corresponding months and sample plots. The coefficients of determination (R2) are 0.61, 0.77, 0.70, 0.67 for May, June, July and August respectively (Figure 3). These assure our confidence in the spatial model (i.e. Equation (5)) of the soil moisture status.
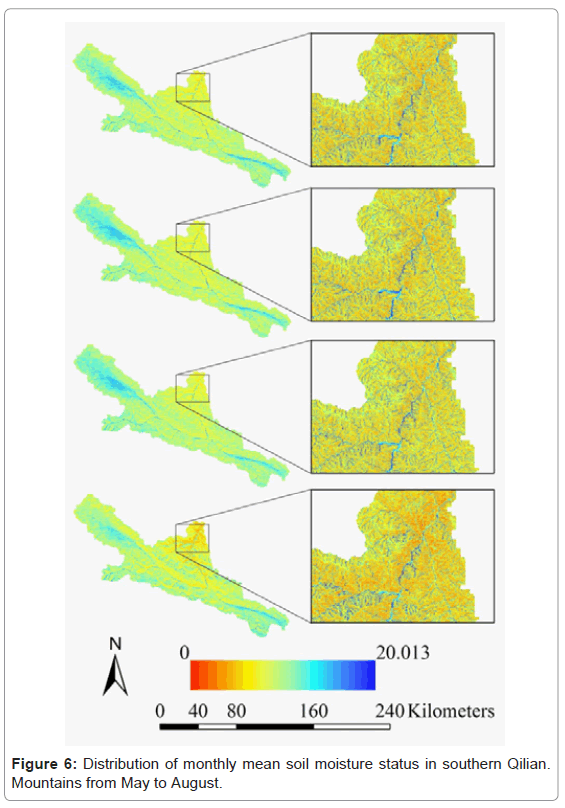
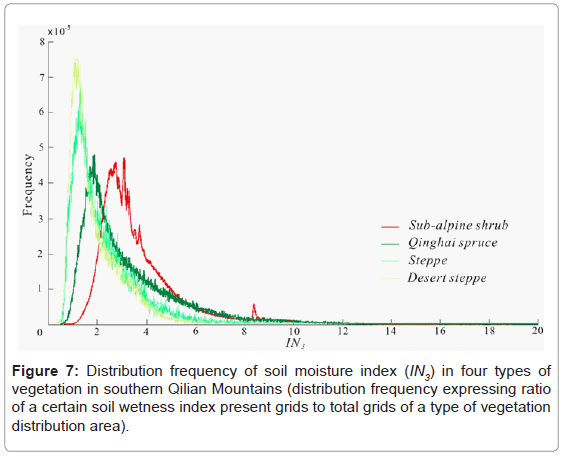
Therefore, the same steps used in Pailuguo catchment were employed to estimate the soil moisture status of the southern Qilian Mountains areas. The maps of the modified wetness index (IN3) in the southern Qilian Mountains were obtained from the models using Grid module in ARC/INFO software (Figure 6). The distribution of the soil moisture status in the southern Qilian Mountains areas reflects the integration of the local topography and landscape climate processes. As viewed from a small scale (Figure 6), locations with a large contributing area receive a high index value and are expected to have relatively higher soil moisture than locations with a small contributing area that are assumed to have relatively lower soil moisture and therefore receive a small index value. Steep locations receive a small index value and are expected to be better drained than gently sloped locations, which receive a high index value. The south-facing slope has lower soil moisture than the north-facing slope because it gets more insolation on the dryness of the soil water. On landscape level, the soil moisture increases from the north to the south and from the low altitude to the high altitude due to the precipitation increase. Figure 6 showed that the driest sites occurred on some ridges in the northern part of the study area, which has very small contributing areas and small precipitation. The wettest sites were registered in the low valleys of the Heihe River and its major tributaries in the eastern part due to large contributing areas and more precipitation. The highest variation of the soil moisture status in the study occurred in July and smaller difference appeared in May. Comparing the four types of vegetation extracted from the present distribution of vegetation with the spatially-modeled results of soil moisture in August for the corresponding locations (Figure 7), we find a certain type of vegetation occupies its special range of the soil moisture. For example, sub-alpine shrub covers the range of soil moisture index (IN3) between 2.19-5.85 with 80% accumulated distribution frequency. Qinghai spruce (Picea crassifolia) dominates the range of soil moisture index (IN3) between 1.46-5.96 with 80% accumulated distribution frequency. Steppe has a range of soil moisture index between 1.00-3.94 with 80% accumulated distribution frequency. Desert steppe covers a range of soil moisture index between 0.92-3.36 with 80% accumulated distribution frequency. Thus it can be seen the spatial distribution pattern of vegetation has nearly relative with that of soil moisture status.
However, the factor of vegetations is not included in Equation (5). Therefore, further studies would be needed to improve the method used in the study incorporating estimated evapotranspiration fluxes of vegetation.
In addition, Soil moisture status is influenced by other factors, such as soil properties, meteorological conditions. The importance of these factors can vary with the study area. Any simple relationship between topographic indices and soil moisture must, however, be used with great care [18,44]. According to Florinsky; in soil studies with digital terrain modelling [45], there is a need to take into account four types of variability besides relief: regional, time, depth, and scale. For example, Chinese Loess Plateau comparing with the southern Qilian Mountains, three natural factors: steeply-sloped topography with gullies, fine-textured loessial soils and precipitation in form of storms are first and foremost considered. These factors decide the unique hydrogeomorphic condition that the rainfall intensity often exceeds the soil infiltration capacity differing from that in the southern Qilian Mountains. So the modified wetness index will be developed (adding model parameters) according to actual conditions in a certain study area.
Conclusions
We can draw some conclusions from the approach:
1. Equation (5) was used to estimate the variability of the soil moisture status in the study area and the model was validated by Pailugou catchment. The results of validation assured our confidence in the spatially-modeled results of the soil moisture status.
2. Equation (5) includes two terms, the changed wetness index and precipitation. The changed wetness index IN2 in Equation (4) is universal in arid and semi-arid areas [46,23,24]. We selected five methods to simulate the temporal-spatial distributions of precipitation in the study. By comparison, the best performance of the linear regression in the study area made this model the best choice.
3. The modified wetness index can be used the Qilian mountains based on validation in Pailugou catchment and on comparison between the pattern of soil moisture status and distribution pattern of vegetation types. The results modeled in the study area will be validated further. We will impose on Equation (5) quite certain regional restrictions.
Acknowledgements
This project was supported by Nation Natural Science Foundation of China (No. 91025015, No. 30770387); National Environmental Protection Commonweal Project of China (NEPCP 200809098).
References
- Ji XB, Kang E, Chen RS (2006) Analysis of Water Resources Supply and Demand and Security of Water Resources Development in Irrigation Regions of the Middle Reaches of the Heihe River Basin, Northwest China. Agricultural Sciences in China 5: 130-140.
- Zhao C, Nan Z, Cheng G (2005) Methods for estimating irrigation needs of spring wheat in the middle Heihe basin, China. J Agwat 75: 54-70.
- Zhao WZ, Liu B, Zhang ZH (2010) Water requirements of maize in the middle Heihe River basin, China. J Agwat 97: 215-223.
- Wang JS, Feng JY, Yang LF (2009) Runoff-denoted drought index and its relationship to the yields of spring wheat in the arid area of Hexi corridor, Northwest China. J Agwat 96: 666-676.
- Famiglietti JS, Wood EF (1994) Multiscale modeling of spatially variable water and energy balance processes. Water Resources Research 30: 3061-3078.
- Li JK, Islam S (1999) On the estimation of soil moisture profile and surface fluxes partitioning from sequential assimilation of surface layer soil moisture. J.Hydrol 220: 86-103.
- Liang X, Lettenmaier DP, Wood EF, Burges SJ (1994) A simple hydrologically based model of land surface water and energy fluxes for general circulation models. Journal of Geophysical Research 14: 415-428.
- Wignosta MS, Vail LW, Lettenmaier DP (1994) A distributed hydrologyvegetation model for complex terrain. Water Resources Research 30: 1665- 1679.
- Cosh MH, Jackson TJ, Bindlish R, Prueger JH (2004) Watershed scale temporal and spatial sta bility of soil moisture and its role in validating satellite estimates. J Rse 92: 427-435.
- Jawson SD, Niemann JD (2007) Spatial patterns from EOF analysis of soil moisture at a large scale and their dependence on soil, land-use, and topographic properties. Advwatres 30: 366-381.
- Manfreda S, McCabe MF, Fiorentino M, Rodríguez-Iturbe I, Wood EF (2007) Scaling characteristics of spatial patterns of soil moisture from distributed modelling. Advwatres 30: 2145-2150.
- Tang C, Piechota TC (2009) Spatial and temporal soil moisture and drought variability in the Upper Colorado River Basin. J Hydrol 379: 122-135.
- Wang J, Fu B, Qiu Y, Chen L, Wang Z (2001) Geostatistical analysis of soil moisture variability on Da Nangou catchment of the loess plateau. China, Environmental Geology 41: 113-120.
- Western A, Grayson R (1998) The Tarrawarra data set: soil moisture patterns, soil characteristics, and hydrological flux measurements. Water Resources Research 34: 2765-2768.
- Western A, Zhou SL, Grayson RB, MacMahon TA, Bloschel G, Wilson D (2004) Spatial correlation of soil moisture in small catchments and its relationship to dominant spatial hydrological processes. J Hydrol 286: 113-134.
- Beven KJ, Kirkby MJ (1979) A physically based, variable contributing area model of basin hydrology. Hydrological Science Bulletin 24: 43-69.
- O'Loughlin EM (1986) Prediction of surface saturation zones in natural catchments by topographic analysis. Water Resources Research 22: 794-804.
- Svetlitchnyi AA, Plotnitskiy SV, Stepovaya OY (2003) Spatial distribution of soil moisture content within catchments and its modelling on the basis of topographic data. J Hydrol 277: 50-60.
- Teuling AJ, Troch PA (2005) Improved understanding of soil moisture variability dynamics. Geophysical Research Letter 32: L05404.
- Cantón Y, Solé-Benet A, Domingo F (2004) Temporal and spatial patterns of soil moisture in semiarid badlands of SE Spain. J Hydrol 285: 199-214.
- Mohanty BP, Skaggs TH (2001) Spatio-temporal evolution and time-stable characteristics of soil moisture within remote sensing footprints with varying soil, slope, and vegetation. Advwatres 24: 1051-1067.
- Qiu Y, Fu BJ, Wang J, Chen LD (2001) Soil moisture variation in relation to topography and land use in a hillslope catchment of the Loess Plateau, China. J Hydrol 240: 243-263.
- Gómez-Plaza A, Martínez-Mena M, Albvaladejo J, Castillo VM (2001) Factors regulating spatial distribution of soil water content in small semiarid catchments. J Hydrol 253: 211-226.
- Moore ID, Burch GJ, Mackenzie DH (1988) Topographic on the distribution of surface soil water and the location of ephemeral gullies. Transactions American Socity Agricultural Engineering 31: 1098-1107.
- Marquínez J, Lastra J, García P (2003) Estimation models for precipitation in mountainous regions: the use of GIS and multivariate analysis. J Hydrol 270: 1-11.
- Dirks KN, Hay JE, Stow CD, Harris D (1998) High-resolution studies of rainfall on Norfolk Island part II: interpolation of rainfall data. J Hydrol 208: 187-193.
- Goovaerts PGrabs T, Seibert J, Bishop K, Laudon H (2009) Modeling spatial patterns of saturated areas: A comparison of the topographic wetness index and a dynamic distributed model. J Hydrol 373: 15-23. (2000) Geostatistical approach for incorporating elevation into the spatial interpolation of rainfall.j.hydrol 228:113-129.
- Guenni L, Hutchinson MF (1998) Spatial interpolation of the parameters of a rainfall model from ground-based data. J Hydrol 212-213: 335-347.
- Price DT, McKenney DW, Nalder IA (2000) A comparison of two statistical methods for spatial interpolation of Canadian monthly mean climate data. Agricultural and Forest Meteorology 101: 81-94.
- Wei H, Li J, Liang T (2005) Study on the estimation of precipitation resources for rainwater harvesting agriculture in semiarid land of China. J Agwat 71: 33- 45.
- Basist A, Bell G.D, Meentemeyer V (1994) Statistical relationships between topography and precipitation patterns. Journal of Climate 7: 1305-1315.
- Goodale CL, Alber JD, Ollinger SV (1998) Mapping monthly precipitation, temperature and solar radiation for Ireland with polynomial regression and digital elevation model. Clim Res 10: 35-49.
- Ninyerola M, Pons X, Roure JM (2000) A methodological approach of climatological modelling of air temperature and precipitation through GIS techniques. Int J Climatol 20: 1823-1841.
- Weisse AK, Bois P (2001) Topographic effects on statistical characteristics of heavy rainfall and mapping in the French Alps. J Appl Meteor 40: 720-740.
- Wotling G., Bouvier C, Danloux J, Fritsch JM (2000) Regionalization of extreme precipitation distribution using the principal components of the topographical environment. J Hydrol 233: 86-101.
- Moore ID, Turner AK, Wilson JP, Jenson SK, Band LE (1993) GIS and landsurface- subsurface process modeling: Environmental modeling with GIS. New York.
- Grayson RB, Western AW, Chiew FHS (1997) Preferred states in spatial soil moisture pattern: local and nonlocal controls. Water Resources Research 33: 2879-2908.
- Dymond CC, Johnson EA (2002) Mapping vegetation spatial patterns from modeled water, temperature and solar radiation gradients. Journal of Photogrammetry and Remote Sensing 57: 69-85.
- Michaud JD, Auvine BA, Penalba OC (1995) Spatial and elevation variations of summer rainfall in the southwestern United States. Journal of Applied Meteorology 34: 2689-2703.
- Lloyd CD (2005) Assessing the effect of integrating elevation data into the estimation of monthly precipitation in Great Britain.j.hydrol 308: 128-150.
- Tsanis IK, Gad MA (2001) A GIS Precipitation method for analysis of storm kinematics. Environental Modelling & Software 16: 273-281.
- Isaaks EH, Srivastava RM (1989) An introduction to applied geostatistics, Oxford University Press.
- Wackernagel H (1995) Multivariate Geostatistics, Springer-Verlag, Berlin.
- Rodhe A, Seibert J (1999) Wetland occurrence in relation to topography: a test of topographic indices as moisture indicators. Agricultural and Forest Meteorology 98-99: 325-340.
- Florinsky IV, Eilers RG, Manning GR, Fuller LG (2002) Prediction of soil properties by digital terrain modelling. Environental Modelling & Software 17: 295-311.
- Grabs T, Seibert J, Bishop K, Laudon H (2009) Modeling spatial patterns of saturated areas: A comparison of the topographic wetness index and a dynamic distributed model. J Hydrol 373: 15-23.
Relevant Topics
- Aquatic Ecosystems
- Biodiversity
- Conservation Biology
- Coral Reef Ecology
- Distribution Aggregation
- Ecology and Migration of Animal
- Ecosystem Service
- Ecosystem-Level Measuring
- Endangered Species
- Environmental Tourism
- Forest Biome
- Lake Circulation
- Leaf Morphology
- Marine Conservation
- Marine Ecosystems
- Phytoplankton Abundance
- Population Dyanamics
- Semiarid Ecosystem Soil Properties
- Spatial Distribution
- Species Composition
- Species Rarity
- Sustainability Dynamics
- Sustainable Forest Management
- Tropical Aquaculture
- Tropical Ecosystems
Recommended Journals
Article Tools
Article Usage
- Total views: 15979
- [From(publication date):
March-2011 - Dec 20, 2025] - Breakdown by view type
- HTML page views : 11265
- PDF downloads : 4714