Spatially Decomposed Low Cloud Amounts and Wavelet Analysis

Spherical harmonics have been used to solve potential problems in physics. One important property of SH is how projections interact with rotations. The SH are closed under rotation. The correspondent rotation matrices are in a block structure, where each band is rotationally independent [1-4]. The rotational invariance for SH is similar to the translational invariance in the Fourier transform [5,6].

In association with SH we have investigated wavelet analysis already used in our previous works [7-11] to show the hidden characteristics in time evolution.

The Continuous Wavelet Transform (CWT) is an ideal tool for mapping the changing properties of non-stationary signals and also to determine whether or not a signal is stationary in a global sense. CWT is then used to build a time-frequency representation of a signal that offers very good time and frequency localization [12-15]. An adjustable parameter controlling the properties of the localized oscillation is generally included in the mother wavelet which can be complex or real.

Morlet wavelets are more powerful in revealing hidden detailed structures. This type of wavelet has been used in our previous work [10] and in other works to examine the processes, models and structures of cosmic rays, solar activity and modulations in low cloud amounts [16-19].

Thus instead of analyzing with Morlet wavelets the apparent time series of LCA we increased our analysis quality by studying the decomposition of LCA in spherical harmonics (eq.1). The obtained components are then submitted to Morlet analysis [12] for the 36 months covering the period between 1990-1992.

Spherical harmonics components of LCA submitted to Morlet analysis

Low cloud amounts expanded into spherical harmonics: Just as the Fourier basis represents an important tool for evaluation of convolutions in a one or two dimensional space, the spherical harmonics basis is a similar tool but defined on the surface of a sphere [20].

Spherical waves propagate isotropically, that is, the wave amplitude is spherically symmetric. We have decomposed values of low cloud amounts (LCA) into spherical harmonics. Then instead of analyzing LCA values directly we have proceeded by decomposing these values in spherical harmonics. Therefore, they are the correspondent components which were analyzed with Morlet wavelets.

Since, spherical harmonics form an orthonormal basis, projecting a spherical function into spherical harmonic coefficients is simple and a straight-forward application of definition (eq.1)

A continuous function 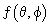can be expanded as a linear combination of spherical harmonics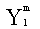

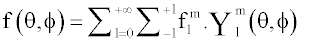(1)

Where l ,m are integer indices, 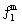is a constant coefficient known in mathematics under the name of generalized Fourier coefficient relative to this base.

The functions where l = 0, are called zonal harmonics (ZH), they have rotational symmetry around the z axis and the zeros (locations where the function is zero) are contours on the sphere parallel to the XY plane.

The functions where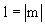 are called sectorial harmonics [21] and the zeros define regions like apple slices.

Everything needed to approximate a given function f with arbitrary accuracy is to compute the coefficients 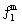describing how much each basis function 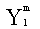is like f .

Generalized and normalized spherical harmonics 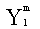are given ^(1-4) in the final form:

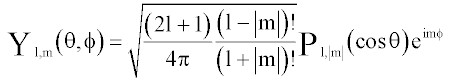(2)

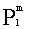is the polynomial of Legendre defined by :

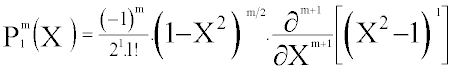(3)

We have examined monthly averaged low cloud cover data [22] from the International Satellite Cloud Climatology Project (ISCCP). For each month the corresponding data table gives the spatial repartition of LCA in latitude and longitude. We have decomposed into spherical harmonics the values of LCA for 36 months covering the period 1990- 1992. We have limited our spherical harmonics decomposition to the first 5 spherical harmonic bands l = 0,.......4 , on the same hand the different m vary : −l..... + l resulting in a total of 25 spherical harmonic components for each month.

Morlet analysis of spherical components for LCA: At this step we have investigated Morlet wavelet already used in previous works [7-11] Morlet wavelet is defined as a complex sine wave, localized with a Gaussian. The frequency domain representation is a single symmetric Gaussian peak. This wavelet incorporates a wave of a certain period, it is finite in extent and is given by:

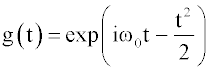(4)

Already wavelet analysis is a useful tool both to find the dominant mode of variation and also to study how it varies with time [15].

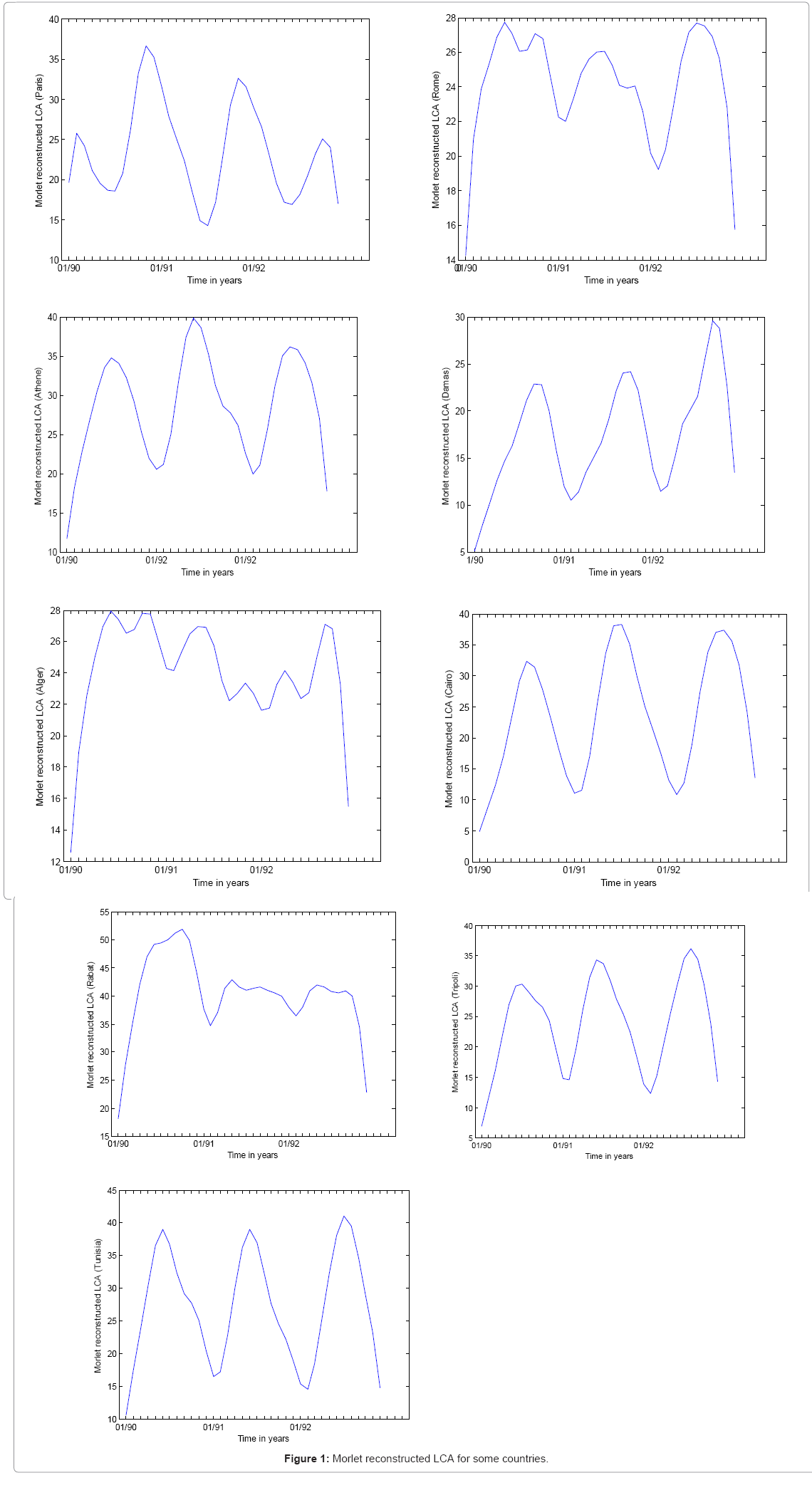
In this paper we have directly decomposed in Morlet wavelets the low cloud amounts relative to some countries for the 36 months covering the period 1990-1992 (Figure 1).

Figure 1: Morlet reconstructed LCA for some countries.

The yearly modulation is clear for all reconstructed variations of LCA. Likewise, a structure of 6 months appears also for Morlet reconstructed LCA variations relative particularly to Rome, Alger and Rabat.

On the other side and looking further for our analysis, we have used Morlet wavelets to study the time variation of the resulting 25 spherical harmonic components 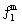(t) of LCA during 36 months between 1990-1992.

For analysis of a discrete signal 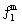(t) and particularly for our case of study we have investigated limited and discrete time series. Therefore the discretized expressions of real parts for Morlet coefficients [10] are then given as follows:

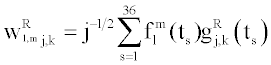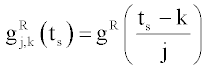, (5)

The phase constant was taken ω₀ = 24π . The period was fixed to T = 1 month

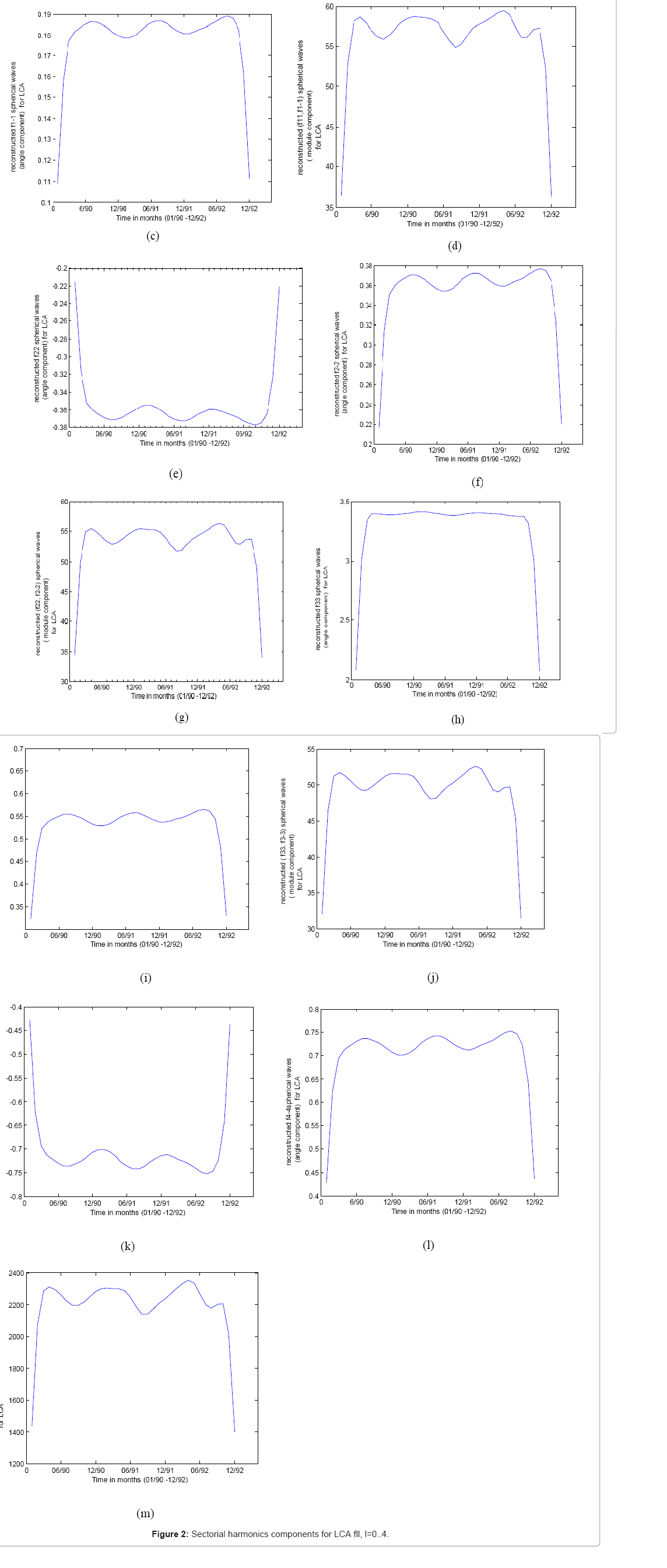
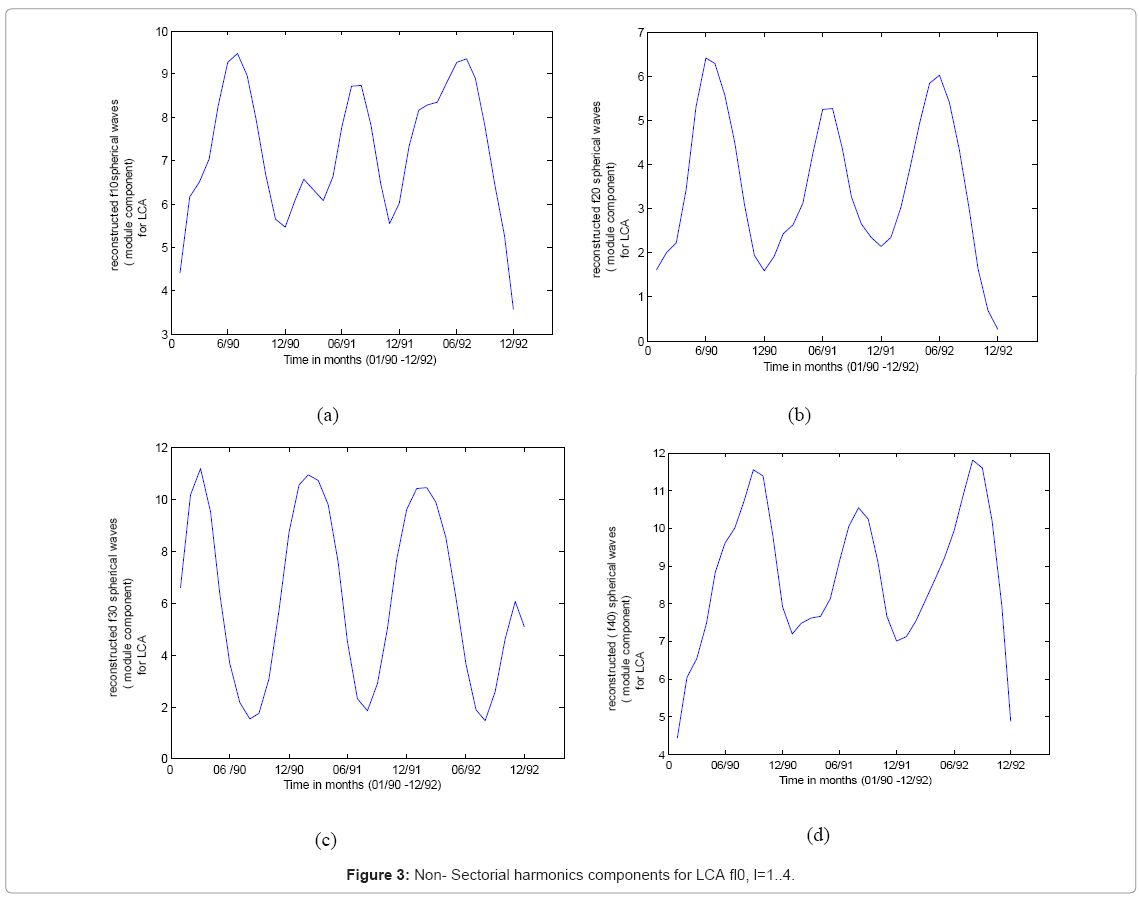
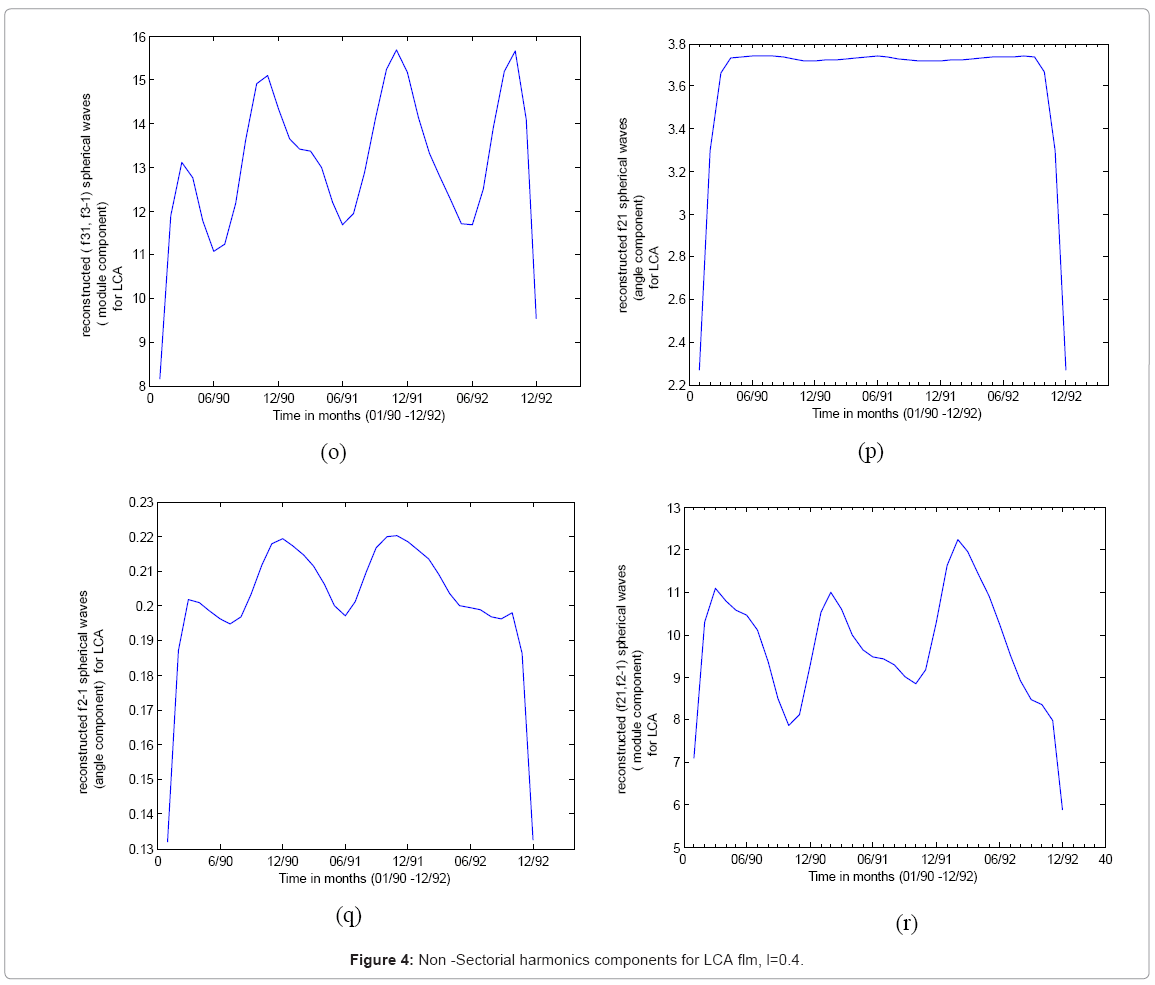
After decomposing the monthly time series relative to each spherical component of LCA, we have reconstructed into Morlet wavelets the 25 spherical harmonics components of LCA. We have obtained 35 reconstructed components considering both parts for the complex components the module and the angle.

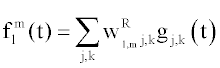(6)

It’s clear that a yearly modulation occurs in all figures (Figures 2-4) for reconstructed spherical harmonics components of LCA and for the whole period of 36 months. The relative maxima of LCA for this period are generally localised around months 11-12 or months 1-3, this is clearer for module components of spherical harmonics. For all sectorial harmonics (Figure 2) and particularly for module components, the shapes of LCA variations are the same, the maxima appear around months 2-3. The angle components present maxima around months 8-9. However the modulation is not very pronounced and is clearer for non-sectorial harmonics. The highest LCA are obtained for the module component f₄₄ , f₄₋₄ . Thus LCA are more condensed in winter, autumn and the beginning of spring relative to spherical harmonics components covering the 3 years 1990-1992.

Figure 2: Sectorial harmonics components for LCA fll, l=0..4.

Figure 3: Non-Sectorial harmonics components for LCA fl0, l=1..4.

Figure 4: Non-Sectorial harmonics components for LCA flm, l=0.4.

A secondary structure around 6 months occurs clearly in the module part of the fourth spherical harmonic component of LCA (Figure 4). Although, the spherical harmonic f₃₋₁ is a maximum in month 6, the minima and the secondary minima relative to these harmonics are generally around months 6-7, thus this means that the lowest amounts of clouds are found in middle of summer which is expected.

Generally we can notice that the most LCA are obtained for winter and spring.

Indeed Sun angle, solar intensity and clouds are important controls of the weather. Clouds are great reflectors of solar energy. This reflected energy is energy that cannot be used to warm the earth’s surface.

The solar intensity is much lower when the sun is closer to the horizon. When the sun is low on the horizon there is a tendency for more clouds in moist climates. This is because a weaker solar intensity produces a weaker evaporative potential. When the solar intensity is strong (sun high in the sky) and the atmosphere is stable, the warming tends to produce less clouds since moisture is evaporated away into the dry air. At the equinox the Sun passes directly overhead at solar noon at the equator. Although the noon solar Sun angle on the equinox is greater than that on the first day of winter, the first remains low inducing also high amounts of clouds [22].

From reconstructed spherical harmonics components of LCA we have detected the yearly modulation. The relative maxima of LCA for this period are generally localised around months 11-12 or months 1-3. The shapes of LCA variations are the same for module components, the maxima appear around months 2-3. The highest LCA are obtained for the module component f₄₄ , f₄₋₄ . Thus LCA are more condensed in winter, autumn and the beginning of spring relative to spherical harmonics.

A secondary structure of 6 months occurs also. The minima and the secondary minima are generally around months 6-7, thus the lowest amounts of clouds are found in middle of summer.

The most LCA are then obtained for winter and spring. Indeed Sun angle, solar intensity and clouds are important controls of the weather. Although the noon solar Sun angle on the equinox is greater than that on the first day of winter, the first remains low inducing also high amounts of clouds.

Spherical harmonics decomposition, already known as “Swiss army knife of mathematical physics” associated with Morlet wavelets expansion greatly increase our analysing tool power. Indeed it seems more rigorous to analyse in time the fine structure of LCA represented by spherical components than to analyse an averaged value of LCA.

We plan to study in another work the correlation between low cloud amounts and solar activity through spherical harmonics decomposition.