Research Article Open Access
Engineered In Vitro Feed-Forward Networks
Anupama Natarajan1, Thomas B. DeMarse2, Peter Molnar3, and James J. Hickman1*1The Nanoscience Technology Center, University of Central Florida, Orlando, FL 32826, USA
2Department of Biomedical Engineering, University of Florida, Gainesville, FL 32611 and the NanoScience Technology Center, University of Central Florida, Orlando, FL 32826, USA
3The Nanoscience Technology Center, University of Central Florida, Orlando, FL 32826, USA. He is now in the Department of Zoology, University of West Hungary, Szombathely, H-9700, Hungary
- Corresponding Author:
- James J. Hickman
University of Central Florida
Nanoscience Technology Center 12424 Research Parkway
Suite 400, Orlando, FL 32826 USA
Tel: 407-823-1925
Fax: 407-882-2819
E-mail: jhickman@mail.ucf.edu
Received date: October 23, 2012; Accepted date: December 14, 2012; Published date: December 14, 2012
Citation: Natarajan A, DeMarse TB, Molnar P, Hickman JJ (2013) Engineered In Vitro Feed-Forward Networks. J Biotechnol Biomater 3:153. doi:10.4172/2155- 952X.1000153
Copyright: © 2013 Natarajan A, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Biotechnology & Biomaterials
Abstract
Keywords
Microelectrode arrays; Directional connectivity ; Axonal polarity; Granger causality; Feed-forward; In vitro
Introduction
Over the last 20 years, a number of methods have been developed to confine the architecture of cultured neuronal networks including microfluidics [1], topographical cues [2,3], microstamping [4], collagen [5], organosilanes [6-11], or alkanethiols [12]. Geometric patterns created include simple lines [13], 4 nodes [14-17] and 8 node interconnected grids [14], loops [18], and even crude logic devices [19]. The engineered geometry of these neuronal networks has been used for the study of plasticity [17] as well as a number of biosensor applications [20-22]. Although a wide variety of methods exist to create desired network geometries, an effective means to engineer neuronal polarity within those geometries has not been established. A relatively simple method that could control directionality within engineered neural patterns would represent an important step toward the construction of model systems for in vivo neuronal architectures.
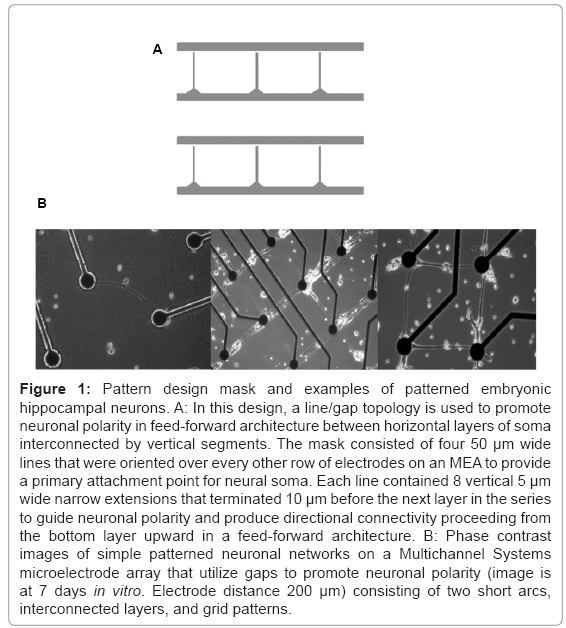
A number of methods have been proposed to guide neuronal polarity. For example, applications of DC fields have shown some promise toward guiding axonal growth [23]. Recently, the combination of Campenot wells [24] that have been interconnected through microtunnel PDMS technology and application of timed plating of neuronal tissue has been reported [25]. Another technique, developed almost 15 years ago, employed patterned silane monolayers [11] and capitalized on the natural tendency of neurons to produce growth cones that follow topological features, including both chemical and structural lines. In this method, chemically patterned line features are narrowed to restrict the number of axons that may follow this feature and simultaneously prohibit the attachment of somas. Small 10 μm gaps at the end of each line are placed near intersections where directionality is desired. Axons following this line feature reach and eventually bridge this short gap to synapse with neural soma on the opposing side (Figure 1A). Axons growing from the opposite direction are not restricted by the narrow line pattern and will not find the small attachment area on the other side of the gap. In this paper, the line/gap feature was employed to create a feed-forward neuronal architecture whose activity was measured using microelectrode arrays. Plasticity was chemically induced to study differences between this architecture and random network controls.
Figure 1: Pattern design mask and examples of patterned embryonic hippocampal neurons. A: In this design, a line/gap topology is used to promote neuronal polarity in feed-forward architecture between horizontal layers of soma interconnected by vertical segments. The mask consisted of four 50 μm wide lines that were oriented over every other row of electrodes on an MEA to provide a primary attachment point for neural soma. Each line contained 8 vertical 5 μm wide narrow extensions that terminated 10 μm before the next layer in the series to guide neuronal polarity and produce directional connectivity proceeding from the bottom layer upward in a feed forward architecture. B: Phase contrast images of simple patterned neuronal networks on a Multichannel Systems microelectrode array that utilize gaps to promote neuronal polarity (image is at 7 days in vitro. Electrode distance 200 μm) consisting of two short arcs, interconnected layers, and grid patterns.
Materials and Methods
Cell culture
Hippocampal neurons were obtained from embryonic day 18 (E- 18) rats and prepared as previously described [26]. Briefly, hippocampi were dissected from the fetuses of timed-pregnant Sprague-Dawley rats. The tissue was mechanically dissociated in a cold serum free dissection solution that contained Hibernate E medium supplemented with B27 (2% v/v; Invitrogen), glutamax (1% v/v; Invitrogen) and antibiotic/ antimycotic (1% v/v; Invitrogen). Prior to cell plating each MEA was sterilized with absolute ethanol and dried. Cells were plated onto 10 MEAs divided into two groups. In Group Directed (n=5), a feed-forward topology composed of UV ablated DETA (N-1[3-(Trimethoxysilyly) propyl] Diethylenetriamine) had been applied (described in the following section) prior to plating and a random topology group, Group Random (n=5) that was unpatterned. Cell density was adjusted to be approximately 200 cells/mm2 in the patterned group and 300 cells/mm2 in the random network control group to compensate for factors such as cell migration and a smaller cell adhesive region relative to silane patterned MEAs. The serum free culture media consisted of Neurobasal supplemented with B27 (2% v/v; Invitrogen), glutamax (1% v/v; Invitrogen) and antibiotic/antimycotic (1% v/v; Invitrogen).
Surface chemistry
Surface preparation: Glass coverslip controls were created for surface chemistry analysis and were cleaned using an acid wash protocol. Briefly, ceramic rack containing glass cover slips were soaked in a solution of 50/50 methanol (HPLC grade)/hydrochloric acid (Reagent grade) for 15-30 min. They were then rinsed with deionized ultra filtered (DIUF) water three times and placed in a beaker containing concentrated sulfuric acid (reagent grade from fisher) for a minimum of 30 minutes. The rack of cover slips was rinsed thoroughly again and boiled in DIUF water for at least 30 minutes. The rack and slips were then rinsed in two final solutions of acetone and oven dried at 110°C for 10-15 min or until dry. The contact angle was then confirmed to be less than 5°. Microelectrode arrays were plasma cleaned for 10 min to avoid damage produced during an acid wash.
Surface modification: The method used for surface modification was similar to those described previously [27,28]. Briefly, ceramic racks with the cleaned surfaces (Glass slips and MEAs) were immersed in a 0.1% (v/v) DETA in HPLC-graded Toluene solvent and heated to just below boiling for 30 min. The solution was then allowed to cool to room temperature. HPLC-graded Toluene was then used to rinse each cover slip and heated for 30 min as before. The surfaces were oven dried for 2 hrs to overnight. After DETA ablation using a deep UV laser (described below), the ablated region was backfilled with 0.1% tridecafluoro-1,1,2,2-tetrahydrooctyl-1-trichlorosilane (13F) in a chloroform solution for 5 min, then rinsed in chloroform, and finally oven dried for 15 min.
Photolithographic pattern
The geometry of the feed-forward network was produced by photolithography exposing the DETA monolayer to 45 seconds of ArF laser irradiation (deep UV 193 nm excimer laser from Lambda Physik at a pulse power of 230 mW and a frequency of 10 Hz) through a quartz mask (Bandwidth foundry, Eveleigh, Australia). The photomask shown in figure 1 consisted of a series of four 50 μm lines that were aligned along electrode rows 2, 4, 6, and 8 on the MEA (top to bottom of the MEA). Each horizontal line had eight 160 μm vertical projections for axonal guidance that extended upward terminating 20 μm before reaching the row above it. During initial platting (including neurons and glia), many cells land outside the patterned surface. However, neurons that land near the horizontal line segments will quickly migrate toward these DETA patterned surfaces forming the horizontal layers of the feed-forward architecture. Once cells had adhered to layers of the architecture, they rapidly begin to extend growth cones within each layer in which they have attached and then toward the neighboring row following the vertical line feature. Neurons within each layer do not tend to extend processes downward across the gap preferring to travel along the much wider line features within each layer [11]. Hence, pathways are primarily constrained to within layers connections among neurons and along the between-layer vertical projections. This architecture is analogous to a feed-forward network in which communication can travel within each layer or between layers in a single direction of communication flow.
Surface characterization
Our laboratory routinely uses self-assembled monolayers to modify and pattern glass surfaces for cell culture applications [8,27,29-32]. XPS is a surface characterization technique used to assess the quality of a DETA/13F modified surface. O2 plasma cleaned, DETA-coated, laser ablated DETA and 13F-coated MEAs were measured using a Thermo ESCALAB 220i-XL X-Ray photoelectron spectrometer equipped with an aluminum anode and a quartz monochromator. Surface charge compensation was achieved using a low-energy electron flood gun and when necessary, by masking the samples with Al foil (a small area was left un-covered for analysis). Survey scans were recorded providing high-resolution spectra for relevant elements on the surface of the MEAs including Si 2p, C 1s, N 1s, and O 1s (pass energy of 50 eV, step size=1eV). The spectrometer was calibrated against the reference binding energies of clean Cu, Ag and Au samples. In addition, the calibration of the binding energy (BE) scale was made by setting the C 1s BE of carbon in a hydrocarbon environment at 285 eV. The N 1s and Si 2p peak deconvolution were performed with Avantage version 3.25 software, provided by Thermo Electron Corporation. For surface wettability, a static drop (5 μL) of deionized water was applied to the sample surface at three different locations and the average contact angle was taken.
Extracellular microelectrode recordings
MEAs were obtained from Multichannel systems and consisted of 59 embedded surface electrodes and one large internal reference electrode. Each 30 μm electrode was spaced 200 μm apart in an 8×8 grid and measured extracellular changes in voltage produced during action potentials of nearby neurons. The data acquisition system consisted of a Multichannel Systems 1060B amplifier (Sampling rate, 25 kHz, Bandwidth 8 Hz to 10 kHz) with temperature control set at 37°C. Raw signals were first filtered offline with a 2nd order Butterworth 300 Hz high-pass filter followed by spike detection using a 5.5 X standard deviation of noise sliding voltage window. Inactive electrodes with a spike rate below 0.02 spikes/sec are likely due to noise and were removed from the analysis. For comparative purposes, only electrode rows 2, 4, 6, and 8 on the MEA were analyzed in each group. Burst detection consisted of the SIMMUX spike time clustering method [33,34]. Media during recordings was replaced with HEPES to control pH and each culture was allowed to stabilize on the rig before the experiment began.
Spontaneous neural activity was recorded in Group Directed and in Group Random for two minutes during each experimental session followed by chemical induction of plasticity using 30 μM 1S, 3R ACPD (Aminocyclopentane-1S, 3R-dicarboxylic acid). ACPD is an agonist for metabotropic glutamate receptors (mGluR) I/II receptors and has been shown to produce long-term potentiation (LTP) and long-term depression (LTD) in hippocampal neurons [35]. Activity was then measured again after two minutes and spike train data were compared before and after treatment.
Analysis
A number of measures were employed to quantify the presence of directional connectivity and assess any changes due to plasticity. Traditional extracellular measures for plasticity including changes in the spike and burst rates were used. Measurement of directional connectivity and any effects of plasticity were quantified using the conditional Granger causality metric. These metric estimates the Granger causal strength and directional information within functional pathways recorded on three or more electrodes and recently applied to spike train data in models [36-38] and in vitro [36]. The idea behind Granger causality can be traced back to Wiener [39] who proposed that two simultaneously measured time series can be said to be causal if incorporating past knowledge this series provides a better prediction of the second series. Clive Granger [40] then formalized this notion using multivariate adaptive auto regression (MVAR). In traditional Granger causality [41], Granger causal values (e.g., causal strength from A- >B and B->A) are determined from time series data between spike trains from two electrodes. The metric is then repeated for each potential electrode pair. While conditional Granger causality [42] provides the same information as Granger causality, it also compensates for the problem of mediated pathways. Consider A->B->C in which A drives activity in B, and B drives activity in C. While GC’s estimate would correctly identify these relationships, it would also indicate a connection between A and C since they are in fact logically and causally but not synoptically connected. However, since A->C is actually mediated through B conditional Granger would correctly remove the A->C relationship. This is an important issue particularly when estimating functional connectivity across large numbers of electrodes where mediating pathways are almost certain to occur across the limited spatial area of the MEA.
Conditional Granger values were calculated from spike trains extracted from each two-minute recording and binned with a 1 ms resolution. Gaussian smoothing was then applied (Half Gaussian window, width 4 ms) to model propagation delays during neural transmission. For this analysis, only active electrodes from rows 2, 4, 6, and 8 were analyzed in Group Directed and Group Random for the purpose of between group comparisons. Conditional Granger causal estimates were calculated using C code based on Anil Seth’s Causal Connectivity Toolbox written in MATLAB [43]. Calculations were performed on an Apple OS X 10 node computer cluster requiring approximately 8 hours to complete. Putative Granger causal pathways were considered significant at the p<0.001 level (F statistic).
Results
Surface modification and analysis
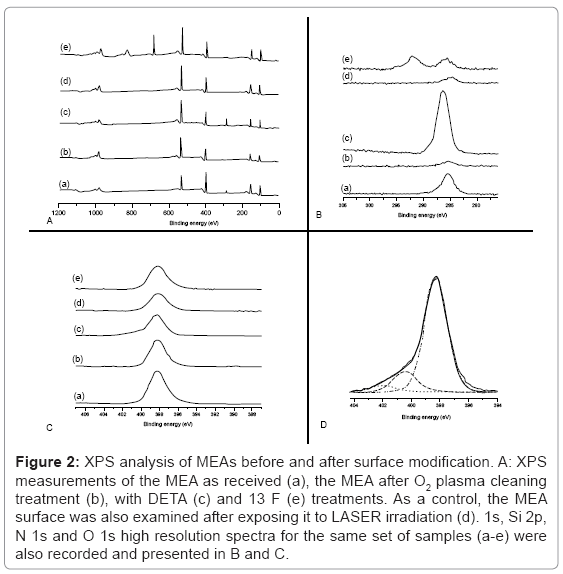
The XPS survey spectra results of the surface modification of an MEA from the initial pristine surface to the final modified surface containing DETA hydrophilic patterns surrounded by a 13F hydrophobic background is depicted in (Figure 2). The chemical composition of MEAs before DETA (Figure 2A (a)) consist largely of silicon (Si 2p=102.2 eV), carbon (C1s=285 eV), nitrogen (N1s=398.2 eV), and oxygen (O1s=533 eV). This chemical composition corresponds to the MEA’s insulation layer (500 nm thickness) that is constructed of Si3N4 (silicon nitride). The silicon nitride surface was slightly oxidized, since a significant O 1s peak was indicated by XPS (Figure 2A (a)). The presence of C in a hydrocarbon environment (C1s=285 eV) is mainly due to carbon contamination most likely through MEA handling. By exposing the MEA to O2 plasma discharge, the surface was cleaned, and only minute traces of carbon (C 1s) were then detectable (Figure 2A (b)). At the same time, there was a noticeable increase in oxygen likely due to plasma cleaning (relative O 1s intensity compared to the Si 2p intensity increased by about 60%).
Figure 2: XPS analysis of MEAs before and after surface modification. A: XPS measurements of the MEA as received (a), the MEA after O2 plasma cleaning treatment (b), with DETA (c) and 13 F (e) treatments. As a control, the MEA surface was also examined after exposing it to LASER irradiation (d). 1s, Si 2p, N 1s and O 1s high resolution spectra for the same set of samples (a-e) were also recorded and presented in B and C.
The chemical composition of the patterned (DETA-coated) and un-patterned (13F-coated) portions of the MEA’s surface are shown in Figure 2A (c and e), respectively. A significant carbon peak centered at 285 eV indicated DETA deposition. This peak was almost completely removed in the XPS survey spectrum of the Laser ablated MEA surface, as seen in Figure 2A (d). For un-patterned MEAs, the 13F-coated portion of the MEA’s surface produced an F 1s peak at about 689 eV, a binding energy characteristic to F in an F-C bond. The C 1s peak was much less intense then the C 1s for DETA-coated portion of the MEA, and was split into 2 peaks. Figure 2B indicates a set of high-resolution C 1s spectra as described above. Clearly, there are 2 main peaks: the first centered at about 285 eV, and it is due either to adventitious C (b and d) or C in a hydrocarbon environment (c and e); the second line shifted about 6 eV to higher binding energy, and was due to CF2 groups of the 13 F (e). Figure 2C shows a set of high-resolution N 1s spectra for the same samples as described above. In all cases there was a dominant peak at about 398 eV, due to the Si3N4 insulation. For the DETA-coated portion of the MEA, besides the Si3N4 dominant feature, there was a second feature much smaller and shifted towards higher binding energy. Figure 2D shows the high-resolution N 1s spectrum of the DETA-coated portion of the MEA, with corresponding curve fitting. The Si3N4 dominant feature is centered at 398.2 eV. The smaller feature consist of 2 lines shifted towards higher binding energy of about 2 eV and 4 eV respectively. These lines are characteristic of amine and protonated amine groups in DETA. Contact angle values were 51 ± 3°, indicative of robust DETA modification.
Analysis of extracellular spike train data
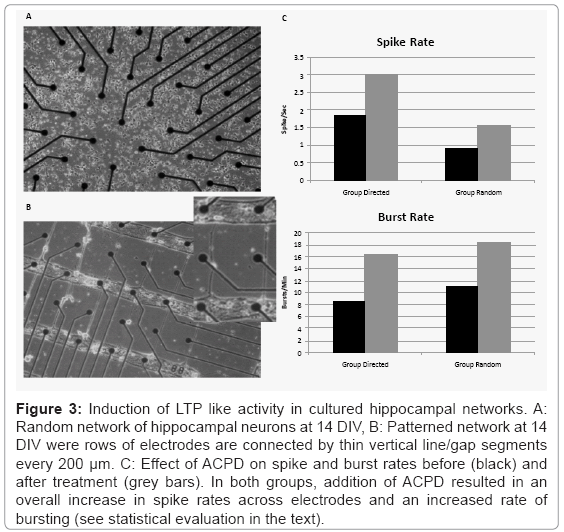
Figure 3 shows an example of two hippocampal cultures. The top row (A) depicts a traditional random culture from Group Random and the bottom row shows an example of a patterned culture from Group Directed using the mask shown in figure 1A. Spontaneous neural activity appeared in both patterned and random cultures as early as day 12 (data not shown). Normal synchronous bursts accompanied by asynchronous neural activity between bursts [44] were observed on many of the MEA electrodes in Group Random and in Group Directed. Figure 3C plots the mean spike (Panel A) and burst rates (Panel B) for Group Directed and Random before and after treatment with ACPD. While the mean spike rate per electrode was higher during baseline in Group Directed (1.85 ± 1.73 spikes-sec) than in Group Random (0.89 ± 0.59 spikes-sec), mean burst rates were lower in Group Directed (8.55 ± 10.17 bursts-min) than Group Random (11.08 ± 11.31 bursts-min). However, these difference were not significant for spike or burst rates (T-test: t(4)<1.25, p>0.28).
Figure 3: Induction of LTP like activity in cultured hippocampal networks. A: Random network of hippocampal neurons at 14 DIV, B: Patterned network at 14 DIV were rows of electrodes are connected by thin vertical line/gap segments every 200 μm. C: Effect of ACPD on spike and burst rates before (black) and after treatment (grey bars). In both groups, addition of ACPD resulted in an overall increase in spike rates across electrodes and an increased rate of bursting (see statistical evaluation in the text).
Treatment with ACPD to induce plasticity increased spike rates in both Directed and Random groups. A split-plot ANOVA indicated that while there was no significant difference between groups (F(1,8)=1.618, p=0.24), there was a significant main effect of ACPD Treatment, (F(1,8)=5.83, p=0.04), and no significant Group X Treatment interaction (F(1,8)=0.335, p=0.58). Although mean burst rates did increase in both groups (4 out of 5 cultures in each group), this increase did not reach significance (F values<2.919, p>0.12).
Assessment of directional connectivity
Conditional Granger causality was applied to the spike data from electrodes in rows 2, 4, 6, and 8 in each group. Overall, the mean number of significant Granger causal pathways was higher in Group Random (105.0 ± 73.99) than Group Directed (36.8 ± 18.63), but this difference during baseline was only marginally significant (t(4)=2.33, p=0.08), and decreased further following ACPD treatment (84.6 ± 75.08, and 34.6 ± 17.68, respectively, t(4)=1.60, p=0.18). In Group Directed, many causal pathways migrate along the relatively wide layers with thin neuronal processes extending upward between each layer. In contrast, connectivity within the random cultures was much more homogeneous with many short pathways and some extending the full length of the electrode grid in a small-world “like” architecture common in cultured random networks [45].
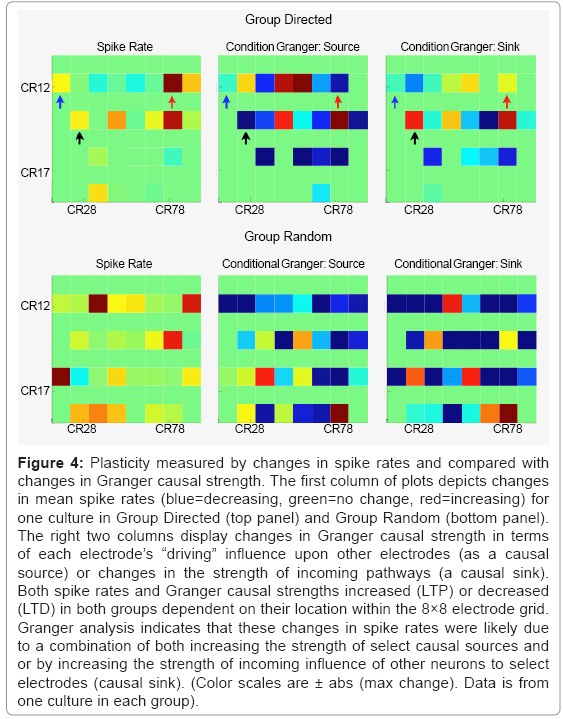
Figure 4 represents the spatial effect of ACPD on Group Directed (Top row) and Group Random (bottom row) based on changes in spike rates and Granger causal strength. For spike rates, both groups showed examples of increased (red) or decreased (blue) spike rates following treatment with ACPD. The direction of this change was also dependent on the location within the network (i.e., electrode grid location). The overall change in mean Granger strength in Group Directed was 0.0005 ± 0.0156 and Group Random was 0.0005 ± 0.0067 indicating a slight positive bias towards potentiating in each group. Similarly, the change in mean spike rates was 0.2883 ± 2.0882 and 0.1205 ± 2.3512 spikes-sec, for Group Directed and Random, respectively. Since Granger causality also provides directional information (e.g., A->B versus B->A) additional detail was provided by separating estimates of Granger causal strength into changes in outgoing (causal source) or incoming (causal sink) causal strength for each electrode. For example, although electrode CR12 (column 1-row 2 on the 8×8 MEA and highlighted with blue arrows) increased spiking following ACPD (left panel), it influences as a causal source driving activity in other neurons decreased (middle panel) and was also influenced less by others (right panel). CR74 (red arrows) increased in strength as a causal source and as a causal sink (right panel) that paralleled an increase in spike rate. In contrast, spike rates on CR 24 (black arrows) increased following ACPD that was not accompanied by an increase in strength as a causal source but as a causal sink.
Figure 4: Plasticity measured by changes in spike rates and compared with changes in Granger causal strength. The first column of plots depicts changes in mean spike rates (blue=decreasing, green=no change, red=increasing) for one culture in Group Directed (top panel) and Group Random (bottom panel). The right two columns display changes in Granger causal strength in terms of each electrode’s “driving” influence upon other electrodes (as a causal source) or changes in the strength of incoming pathways (a causal sink). Both spike rates and Granger causal strengths increased (LTP) or decreased (LTD) in both groups dependent on their location within the 8×8 electrode grid. Granger analysis indicates that these changes in spike rates were likely due to a combination of both increasing the strength of select causal sources and or by increasing the strength of incoming influence of other neurons to select electrodes (causal sink). (Color scales are ± abs (max change). Data is from one culture in each group).
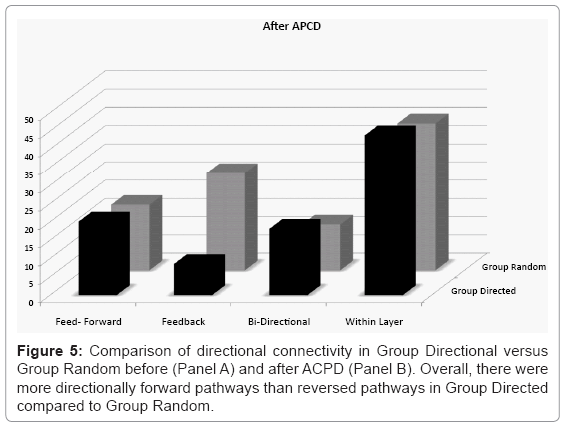
To quantify whether line/gap features promoted directional feed-forward pathways between each layer the results from the conditional Granger analysis were then subdivided into pathways between layers and analyzed in detail for their directional content. Figure 5 separates each significant Granger causal pathway into the mean percentage of total pathways that were uniquely feed-forward (with no reciprocal feedback connection along that path), uniquely feedback, bi-directional relations, and the percentage of pathways that were within layer before (Panel A) and after (Panel B) treatment with ACPD. The only observed difference between the two groups was an asymmetry between feed-forward and feedback pathways in Group Directional which was not present in Group Random. The mean percent pathways in the engineered unique forward direction was higher than unique reversed in Group Directed (paired T-Test, t(4)=2.28, p=0.08) whereas the values were similar in Group Random (paired T-Test, t(4)=0.38, p=0.73). There was no significant difference between Group Directed and Group Random in terms of feed-forward pathways (t(4)=0.75, p=0.49). In contrast, feedback connection were significantly less in Group Directed than in Group Random (t(4)=2.81, p=0.05). Between group comparison of the total feed-forward versus feedback pathways (irrespective of the presence of reciprocal relations) was also higher in Group Directed (34.77% versus 27.57%, paired t-test, t(4)=2.28, p=0.08) but equivalent in Group Random (31.85% and 32.96%, paired t-test, t(4)=0.37, p=0.73). The percentage of pathways falling within each layer was similar across groups (t(4)=0.05, p=0.96) as were the number of pathways that were bi-directional (t(4)=1.02, p=0.37).
Figure 5: Induction of LTP like activity in cultured hippocampal networks. A: Random network of hippocampal neurons at 14 DIV, B: Patterned network at 14 DIV were rows of electrodes are connected by thin vertical line/gap segments every 200 μm. C: Effect of ACPD on spike and burst rates before (black) and after treatment (grey bars). In both groups, addition of ACPD resulted in an overall increase in spike rates across electrodes and an increased rate of bursting (see statistical evaluation in the text).
Treatment with ACPD did not appear to affect the overall number of pathways relative to baseline. For example, there were significantly less feedback pathways in Group Directed relative to Group Random (t(4)= 2.98, p=0.04) seen before ACPD, there was an equivalent percentage of feed-forward pathways (t(4) = 0.20, p = 0.85), bi-directional (t(4)=0.55, p=0.61) pathways, and pathways within each layer (t(4)=0.24. p=0.82). There were also no significant change in the percentage of each type of pathway before versus after ACPD treatment (t(4)<0.62, p>0.56).
Discussion
In this study, directional connectivity was engineered using DETA patterned line/gap topology that enhanced the conformation of neuronal soma into layers and promoted axonal polarity to create feed-forward architecture. Both patterned and random controls were spontaneously active producing both asynchronous and network wide bursts within 12 days after plating. Our results indicate that the line/gap topology did promote the development of a feed-forward network. As expected the majority of pathways occurred in the much wider horizontal layers. In terms of specific layer-to-layer connectivity, the number of feed-forward connections was equivalent in Group Directed versus Group Random. There were significantly fewer feedback connections in Group Directed relative to random controls indicative of the bias produced by the line/gap features. There were also a slightly higher number of bi-directional pathways in Group Directed relative to Group Random, but not significantly so. For the bi-directional pathways, there was also greater variability between cultures in Group Directed (19.84 ± 18.60) relative to random controls (9.97 ± 10.73). This difference may reflect an increasing potential as time in culture increases for axons from neighboring layers to migrate back along established axons along the feed-forward pathway. By comparison, any return paths in Group Random (e.g., between an electrode pair) would be expected to be spatially and uniformly distributed due to the lack of any specific confinement. The number of within-line (row) pathways was also equivalent between both groups indicating that the horizontal lines in Group Patterned did not adversely affect the probability of the formation of horizontal pathways compared to random networks where connectivity was unconfined.
Application of ACPD to induce plasticity within these networks resulted in an overall increase in spike rates and accompanying increase in bursting in both Groups. In this study, we employed the conditional Granger causality metric to provide greater detail about the nature and direction of these changes. This metric has been shown to successfully capture LTP and LTD following tetanic stimulation in random cultures on MEAs [36] and measure the effect of plasticity on functional connectivity. Analyzing plasticity is, however, a difficult problem in random cultures due to their inherent network complexity and this paper represents the first time the Granger metric has been applied to conditions where information about underlying neuron to neuron connectivity is highly constrained and therefore, much better defined.
As expected, addition of ACPD enhanced spike and burst rates in both groups. However, comparisons among individual electrodes indicated cases where although spiking appeared to increase causal strength may decrease as a causal source but increase as a causal sink. This may be indicative of occasions where the synaptic strength of incoming connections increased in the absence of an increase of output synaptic weights upon other neurons in the network. Similarly, both the rate of spiking and Granger causal strength as a causal source increased but decreased as a causal sink indicative of a neuron whose influence on the network has increased and was less affected by others. These effects are analogous to those shown following tetanic stimulation on MEAs that also produced potentiation and depression in random cultured networks [46-48], in patterned cultures [49], via patch clamp [17], and analyzed using conditional Granger [36]. It is also possible for an increase in spiking to correspond to a decrease in causal strength as a causal source if that spiking neuron happened to increase spiking of an inhibitory neuron (e.g., due to increased excitatory inputs) would likely produce a decrease in activity in its synaptic targets leading to decrease Granger causal strength. One of the advantages of employing the Granger causality metric is that it is relatively immune to changes in spiking simply due to noise. While an increase in spiking is indicative of plasticity in a traditional metric, that increase may not result in increased Granger causal strength since Granger causality provides a measure of the predictive power of activity from one neuron upon the activity of another. Hence, increased spiking in the absence of increased coupling to another neuron’s activity does not affect causal strength. Moreover, conditional Granger has the advantage of disambiguating interactions that are actually caused by mediating neurons (A problem that is difficult to overcome unambiguously with other metrics such as cross-correlation).
Conclusion
Unique line/gap patterns were used to promote a directional feed-forward like neural architecture. Axonal polarity was measured using activity measured by multichannel microelectrode arrays and quantified using conditional Granger causality analysis. Plasticity was then induced to determine whether 1) LTP/LTD are supported in this new architecture and 2) whether those changes were different in feed-forward relative to random network controls. It was shown that this new pattern does promote a bias towards feed-forward relative to feedback pathways, but was otherwise very similar to control cultures in terms of plasticity and number of pathways within each layer. Similar numbers of bi-directional pathways were also observed and may be due to the eventual bridging of axons traversing back along feed-forward pathways. Perhaps reducing the width of vertical segments or larger gaps may improve conformity over longer-term culturing, but this will need to be tested in the future studies.
The formation of well-defined networks with constrained topologies that include directionality represent an important step toward the goal of establishing viable in vitro models of in vivo neural architectures. This technology may have applications in neuronal biosensor design or in drug discovery and toxicity testing that is targeted toward a specific brain area where a well defined neuronal architecture coupled with specific directional connectivity can be used in a relatively high throughput system.
Acknowledgements
This work was supported in part by NIH Grant R01EB005459 and gift from Unither Neurosciences.
References
- Morin F, Nishimura N, Griscom L, Lepioufle B, Fujita H, et al. (2006) Constraining the connectivity of neuronal networks cultured on microelectrode arrays with microfluidic techniques: A step towards neuron-based functional chips. Biosens Bioelectron 21: 1093-1100.
- Curtis AS, Wilkinson CD (1998) Reactions of cells to topography. J Biomater Sci Polym Ed 9: 1313-1329.
- Dowell-Mesfin NM, Abdul-Karim MA, Turner AM, Schanz S, Craighead HG, et al. (2004) Topographically modified surfaces affect orientation and growth of hippocampal neurons. J Neural Eng 1: 78-90.
- Corey JM, Wheeler BC, Brewer GJ (1996) Micrometer resolution silane-based patterning of hippocampal neurons: Critical variables in photoresist and laser ablation processes for substrate fabrication. IEEE Trans Biomed Eng 43: 944-955.
- Matsuda T, Sugawara T, Inoue K (1992) Two-dimensional cell manipulation technology. An artificial neural circuit based on surface microphotoprocessing. ASAIO J 38: M243-M247.
- Hickman JJ, Bhatia SK, Quong JN, Shoen P, Stenger DA, et al. (1994) Rational pattern design for in-vitro cellular networks using surface photochemistry. J Vac Sci Technol 12: 607-616.
- Kleinfeld D, Kahler KH, Hockberger PE (1988) Controlled outgrowth of dissociated neurons on patterned substrates. J Neurosci 8: 4098-4120.
- Murugan R, Molnar P, Rao KP, Hickman JJ (2009) Biomaterial surface patterning of self assembled monolayers for controlling neuronal cell behavior. Int J Biomed Eng Technol 2: 104-134.
- Ravenscroft MS, Bateman KE, Shaffer KM, Schessler HM, Jung DR, et al. (1998) Developmental neurobiology implications from fabrication and analysis of hippocampal neuronal networks on patterned silane-modified surfaces. J Am Chem Soc 120: 12169-12177.
- Stenger DA, Georger JH, Dulcey CS, Hickman JJ, Rudolph AS, et al. (1992) Coplanar molecular assemblies of aminoalkylsilane and perfluorinated alkylsilane-characterization and geometric definition of mammalian-cell adhesion and growth. J Am Chem Soc 114: 8435-8442.
- Stenger DA, Hickman JJ, Bateman KE, Ravenscroft MS, Ma W, et al. (1998) Microlithographic determination of axonal/dendritic polarity in cultured hippocampal neurons. J Neurosci Methods 82: 167-173.
- Lopez GP, Albers MW, Schreiber SL, Carroll R, Peralta E, et al. (1993) Convenient methods for patterning the adhesion of mammalian-cells to surfaces using self-assembled monolayers of alkanethiolates on gold. J Am Chem Soc 115: 5877-5878.
- Feinerman O, Segal M, Moses E (2005) Signal propagation along unidimensional neuronal networks. J Neurophysiol 94: 3406-3416.
- Boehler MD, Leondopulos SS, Wheeler BC, Brewer GJ (2011) Hippocampal networks on reliable patterned substrates. J Neurosci Methods 203: 344-353.
- Branch DW, Wheeler BC, Brewer GJ, Leckband DE (2000) Long-term maintenance of patterns of hippocampal pyramidal cells on substrates of polyethylene glycol and microstamped polylysine. IEEE Trans Biomed Eng 47: 290-300.
- Jun SB, Hynd MR, Dowell-Mesfin N, Smith KL, Turner JN, et al. (2007) Low-density neuronal networks cultured using patterned poly-l-lysine on microelectrode arrays. J Neurosci Methods 160: 317-326.
- Vogt AK, Wrobel G, Meyer W, Knoll W, Offenhäusser A (2005) Synaptic plasticity in micropatterned neuronal networks. Biomaterials 26: 2549-2557.
- Feinerman O, Moses E (2006) Transport of information along unidimensional layered networks of dissociated hippocampal neurons and implications for rate coding. J Neurosci 26: 4526-4534.
- Feinerman O, Rotem A, Moses E (2008) Reliable neuronal logic devices from patterned hippocampal cultures. Nat Phys 4: 967-973.
- Chang JC, Brewer GJ, Wheeler BC (2001) Modulation of neural network activity by patterning. Biosens Bioelectron 16: 527-533.
- Khatami D, Nam Y, Brewer G, Wheeler B (2004) Effect of bicuculline on the spontaneous and evoked activity of patterned embryonic hippocampal neurons cultured in vitro. Conf Proc IEEE Eng Med Biol Soc 6: 4059-4062.
- O'Connor SM, Stenger DA, Shaffer KM, Maric D, Barker JL, et al. (2000) Primary neural precursor cell expansion, differentiation and cytosolic Ca(2+) response in three-dimensional collagen gel. J Neurosci Methods 102: 187-195.
- McCaig CD, Rajnicek AM, Song B, Zhao M (2002) Has electrical growth cone guidance found its potential? Trends Neurosci 25: 354-359.
- Campenot RB (1977) Local control of neurite development by nerve growth factor. Proc Natl Acad Sci U S A 74: 4516-4519.
- Pan L, Alagapan S, Franca E, Brewer GJ, Wheeler BC (2011) Propagation of action potential activity in a predefined microtunnel neural network. J Neural Eng 8: 046031.
- Huettner JE, Baughman RW (1986) Primary culture of identified neurons from the visual cortex of postnatal rats. J Neurosci 6: 3044-3060.
- Das M, Bhargava N, Gregory C, Riedel L, Molnar P, et al. (2005) Adult rat spinal cord culture on an organosilane surface in a novel serum-free medium. In Vitro Cell Dev Biol- Animal 41: 343-348.
- Das M, Wilson K, Molnar P, Hickman JJ (2007) Differentiation of skeletal muscle and integration of myotubes with silicon microstructures using serum-free medium and a synthetic silane substrate. Nat Protoc 2: 1795-1801.
- Molnar P, Wang W, Natarajan A, Rumsey JW, Hickman JJ (2007) Photolithographic patterning of C2C12 myotubes using vitronectin as growth substrate in serum-free medium. Biotechnol Prog 23: 265-268.
- Natarajan A, Molnar P, Sieverdes K, Jamshidi A, Hickman JJ (2006) Microelectrode array recordings of cardiac action potentials as a high throughput method to evaluate pesticide toxicity. Toxicol In Vitro 20: 375-381.
- Natarajan A, Stancescu M, Dhir V, Armstrong C, Sommerhage F, et al. (2011) Patterned cardiomyocytes on microelectrode arrays as a functional, high information content drug screening platform. Biomaterials 32: 4267-4274.
- Varghese K, Molnar P, Das M, Bhargava N, Lambert S, et al. (2010) A new target for amyloid beta toxicity validated by standard and high-throughput electrophysiology. PLoS One 5: e8643.
- Dockendorf KP, Park I, He P, Principe JC, DeMarse TB (2009) Liquid state machines and cultured cortical networks: the separation property. Biosystems 95: 90-97.
- Wagenaar DA, Pine J, Potter SM (2006) An extremely rich repertoire of bursting patterns during the development of cortical cultures. BMC Neurosci 7: 11.
- Gallagher JP, Zheng F, Shinnick-Gallagher P (1994) Long-lasting modulation of synaptic transmission by metabotropic glutamate receptors, in the metabotropic glutamate receptors. Humana Press, Totowa, New Jersey.
- Cadotte AJ, DeMarse TB, He P, Ding M (2008) Causal measures of structure and plasticity in simulated and living neural networks. PLoS One 3: e3355.
- Kim S, Putrino D, Ghosh S, Brown EN (2011) A Granger causality measure for point process models of ensemble neural spiking activity. PLoS Comput Biol 7: e1001110.
- Nedungadi AG, Rangarajan G, Jain N, Ding M (2009) Analyzing multiple spike trains with nonparametric Granger causality. J Comput Neurosci 27: 55-64.
- Wiener N (1956) The theory of prediction, in modern mathematics for the engineer. McGraw-Hill, New York.
- Granger CWJ (1969) Investigating causal relations by econometric models and cross-spectral methods. Econometrics 37: 424-438.
- Schelter B, Vinterhalder M, Timmer J (2006) Handbook of time series analysis: Recent theoretical developments and applications, Wiley-VCH Verlag GMBh & Co: Berlin.
- Chen Y, Bressler SL, Ding M (2006) Frequency decomposition of conditional Granger causality and application to multivariate neural field potential data. J Neurosci Methods 150: 228-237.
- Seth AK (2010) A MATLAB toolbox for Granger causal connectivity analysis. J Neurosci Methods 186: 262-273.
- Van Pelt J, Corner MA, Wolters PS, Rutten WL, Ramakers GJ (2004) Longterm stability and developmental changes in spontaneous network burst firing patterns in dissociated rat cerebral cortex cell cultures on multielectrode arrays. Neurosci Lett 361: 86-89.
- Shefi O, Golding I, Segev R, Ben-Jacob E, Ayali A (2002) Morphological characterization of in vitro neuronal networks. Phys Rev E Stat Nonlin Soft Matter Phys 66: 021905.
- Chiappalone M, Casagrande S, Tedesco M, Valtorta F, Baldelli P, et al. (2009) Opposite changes in glutamatergic and GABAergic transmission underlie the diffuse hyperexcitability of synapsin I-deficient cortical networks. Cereb Cortex 19: 1422-1439.
- Jimbo Y, Tateno T, Robinson HP (1999) Simultaneous induction of pathway-specific potentiation and depression in networks of cortical neurons. Biophys J 76: 670-678.
- Tateno T, Jimbo Y (1999) Activity-dependent enhancement in the reliability of correlated spike timings in cultured cortical neurons. Biol Cybern 80: 45-55.
- Suzuki I, Yasuda K (2007) Detection of tetanus-induced effects in linearly lined-up micropatterned neuronal networks: application of a multi-electrode array chip combined with agarose microstructures. Biochem Biophys Res Commun 356: 470-475.
Relevant Topics
- Agricultural biotechnology
- Animal biotechnology
- Applied Biotechnology
- Biocatalysis
- Biofabrication
- Biomaterial implants
- Biomaterial-Based Drug Delivery Systems
- Bioprinting of Tissue Constructs
- Biotechnology applications
- Cardiovascular biomaterials
- CRISPR-Cas9 in Biotechnology
- Nano biotechnology
- Smart Biomaterials
- White/industrial biotechnology
Recommended Journals
Article Tools
Article Usage
- Total views: 15345
- [From(publication date):
May-2013 - Dec 18, 2025] - Breakdown by view type
- HTML page views : 10480
- PDF downloads : 4865