Research Article Open Access
A Discrete Event Based Stochastic Simulation Platform for ‘In silico’ Study of Molecular-level Cellular Dynamics
Samik Ghosh1, Preetam Ghosh2*, Kalyan Basu3, Sajal K Das3 and Simon Daefler41The Systems Biology Institute (SBI), 6-31-15 Jingumae M31 6A, Shibuya, Tokyo 150-0001 Japan
2Department of Computer Science, Virginia Commonwealth University, Richmond, VA-23284, USA
3Dept. of Comp. Sc. & Engg., The University of Texas at Arlington, Arlington, Texas, 76019-0015, USA
4Division of Infectious Diseases, Mount Sinai School of Medicine, New York, USA
- Corresponding Author:
- Preetam Ghosh
Department of Computer Science
Virginia Commonwealth University
Richmond, VA-23284, USA
E-mail: pghosh@vcu.edu
Received date: June 23, 2010; Accepted date: August 28, 2011; Published date: August 30, 2011
Citation: Ghosh S, Ghosh P, Basu K, Das SK, Daefler S (2011) A Discrete Event Based Stochastic Simulation Platform for ‘In silico’ Study of Molecular-level Cellular Dynamics. J Biotechnol Biomaterial S6:001. doi:10.4172/2155-952X.S6-001
Copyright: © 2011 Ghosh S, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Biotechnology & Biomaterials
Keywords
In silico modeling and simulation; Stochastic modeling; Discrete event simulation; Bio-simulation
Introduction
Traditionally, the key focus of biology has been on detailed understanding of single genes, molecules or processes involved in particular phenotypic manifestations. This powerful approach has resulted in a significant understanding of the structure and function of individual genes and proteins. In the recent past, with the development of high throughput micro array experiments and bio chips, an explosive amount of empirical data on the molecular foundations of biological structures and functions [1] have been opened up to researchers. Complete genomic sequencing of new organisms has been completed and advanced databases like Genome Bank (GenBank), Protein Database (PDB), which store comprehensive annotations of genomic and protein structures, are being developed at previously unimaginable rates. Concomitant with this development, a large body of knowledge is being derived from different biological pathways activated by different regulatory genes, hormones and metabolic reactions through fluorescence tagging and other types of advanced in-vitro experiments. These results are captured in a large volume of scientific papers and experimental data in PubMed [2] and other databases. However, as more and more data become available, biologists are now looking beyond 2 assigning functions to individual genes – focusing on dynamic processes, interdependent regulatory controls, and the operation of multiple interacting components [3].
The fundamental challenge in a “wholistic” understanding of biological processes is the complexity involved in the interaction of different components, coupled with the knowledge gap which exists in a complete characterization of their molecular mechanics. The complexity and knowledge gap increases manifold as we move into higher scales such as interaction of large ensemble of cells in a tissue, or interaction of tissues in continuum for rhythmic pumping of the heart [4]. The challenge [3] is to develop a modeling technique that can easily integrate the molecular and genetic data together with available pathway and system knowledge, for a quantitative understanding of physiology and behavior of biological processes at multiple scales: starting from the cell, to the tissue, and finally to the level of whole organisms
In recent years, researchers from diverse backgrounds of physical sciences, mathematics, biological and computational sciences have collaborated on developing models which capture the dynamics of biological processes. Continuous system models [5-9], which employ differential equations to simulate cellular dynamics, have been extensively used in tools like Dizzy [9] and JARNAC [6]. Stochastic discrete time models, like StochSim [10] and M-cell [11], have been developed for capturing the stochastic nature of molecular interactions within the existing framework of rate equations in continuous time domain. Most of these models focus on intracellular biochemical reactions and require accurate estimation of a very large number of system parameters for providing systemic understanding of underlying processes. More integrative tools at the whole cell level have also been developed, which try to model cellular mechanisms and present visual representation of their functionality [12-14]. Appreciating the need for quantitative techniques to understand the systemic behavior of complex cellular processes, a rich body of literature, particularly in the modeling and simulation (M&S) landscape has been developed for systems biology in the past few years. We provide a taxonomic study of the existing techniques in Section 2.
With the existing systems in perspective, we present a discreteevent based stochastic simulation system to study the process dynamics in cells. The central theme of our approach revolves around abstracting a complex biological process as a collection of interacting functions driven in time by a set of discrete molecular events. Analyzing the system at a molecular level, the temporal dynamics of the system are revealed by the interaction of these events. The stochastic behavior of the interactions is captured through the mathematical formalism characterizing the time associated with each of the biological events, i.e. the event holding time models. The discrete event models create the biological process description in time, while the simulation captures the interaction of these processes through the events to create the dynamics of the biological system. We outline the details of our modeling approach in Section 3. In order to evaluate the success of our technique, we study a test bed biological process, namely the effect of the two component PhoPQ virulence gene regulatory network in Salmonella Typhimurium pathogenesis. Using this test bed, we develop our simulation systems and methods in Section 4. We present the software architecture of our platform, iSimBioSys, in Section 5. In Section 6, we report results on the dynamics of the PhoPQ pathway under the influence of extra cellular magnesium, in silico and corroborate the results with wet-lab experimental outputs. Our results show that stochastic modeling of molecular events, linked through a discrete event based simulation platform, is capable of effectively modeling cell-level molecular pathway dynamics while allowing various “dry lab” hypothesis testing prior to developing novel wet-lab experiments. Although, currently focused on modeling cell-level pathways, our discrete event based biosimulation tool can be extended for multi-scale simulation of complex processes, which is outlined in the conclusions in Section 7.
Modeling and S imulation Landscape
The inherent complexity involved in the molecular processes governing life has motivated the development of computational modeling and simulation techniques to decipher their ensemble dynamics. Particularly, in the post-genomic era, biology has undergone a paradigm shift from being an “observational science” to a quantitative discipline, powered by large scale databases, computational power and advanced, high throughput experiments. In this section, we provide an overview of the wide spectrum of in silico modeling and simulation methodologies available for system-wide study of biological processes.
Mathematical models have being extensively used for intracellular molecular networks like kinase cascades and metabolic pathways, gene regulatory networks and protein interaction networks [15]. A large section of the work in computational models of biological systems is based on classical chemical kinetic (CCK) formalism based on a set of ordinary differential equations (ODE), also known as reaction rate equations or mass action kinetics [16]. Representing a homogeneous biological system as a set of biochemical reactions, the temporal dynamics of the molecular species is studied in the continuousdeterministic domain. A large number of computational tools, which provide a software platform for building, storing and parameterizing a set of biochemical reactions and solving those using numerical techniques, are available, like Gepasi [5], Jarnac [6], CyberCell [11], Promot/DIVA [17], Stode [18]. These rate-based models have been successfully applied to study gene expression and other molecular reaction systems [15].
While continuous-deterministic reaction models are capable of capturing behavorial dynamics for spatially homogeneous systems with large number of molecular species, the inherent stochasticity observed in many biological processes (gene expression and protein synthesis) have proven the limitation of CCK in accurately representing biological processes. In a recent article [16], Arkin et.al have shown the limitations of CCK in several common biological scenarios, where stochastic reaction dynamics present a more accurate picture of the systems behavior. Stochastic models, which present an accurate approximation for the chemical master equation (CME), have been developed, largely based on Gillespie’s algorithm [19,20]. In this method, as shown in a later section, the next reaction event and the time associated with it are computed based on a probability distribution (Monte Carlo Step). Stochastic tools, like StochSim [10], have been developed based on Gillespie’s technique and its computationally efficient variants like Gibson-Bruck [21] and tau-leaping [22-24]. A large number of tools, which provide an integrative environment to build and study biochemical reaction systems in an exchangeable format (like Systems Biology Markup Language (SBML)) using deterministic as well as stochastic techniques are available, like E-Cell (Table 1), Virtual Cell [25], Dizzy [9], CyberCell, and M-Cell (Table 1). These techniques are based on treating a biological process as a system of equations, represented by their rate constants and other parameters (like volume, cell density etc.) and simulating their interactions through numerical techniques or Monte Carlo based stochastic simulations.
| M&S tool | Modeling Technique | Spatial Representation |
Temporal Evolution | Reaction Model | Comments & Availabilityq |
| Promot/DIVA | 00 paradigm | Not explicity defined |
Continuous time | CCK | http://megdeburg.mpg.de/de/ research/projects/1002/comp_ bio/promot |
| JARNAC | ODE based | Not explicity defined |
Continuous time | CCK | http://www.sys-bio.org |
| V-Cell | Continuous domain | Compartments, sub volumes |
Continuous time | CCK, Mass action | http://www.vcell.org |
| M-Cell | Monte Carlo simulator of cellular micro physiology | Off lattice | Time-step driven | At surfaces, CME | http://www.mcell.pse.edu |
| E-Cell | Object-oriented software suite for modeling, simulation, and analysis of complex systems |
Compartmental | Supports CCK/SSA | CCK, CME | http://www.e-cell.org |
| SimBiology | Primarily ODE based simulation package | Not explicity defined |
Supports CCK/SSA | CCK, CME | The Math Works Inc. |
| Dizzy | Stochastic simulation package | Compartmental | Supports CCK/SSA | CCK, CME | ISB, Sealtle, WA |
| Cellerator | Mathematical package for automatic equation generation and simulation for network of cells |
Not explicity defined |
Continuous time | CCK | http://www.cellerator.info |
| Agent Cell | Agent based simulation of biological systems | Not explicity defined |
Time-step driven | Agents model molecular behavior |
http://www.agentcell.org |
| FURM | Functional unit representation of biological processes |
Not explicity defined |
Continuous time | Functional modeling | http://biosystems.ucesf.edu/ Research/furm/index.html |
| Stochastic II calculus |
Abstract model of system based on DEVs | Cellular compartments |
Continuous/discrete time steps |
Processes model molecules/domain, communications model reactions |
[30,31] |
| Stochastic Petrinets |
Stochastic model of molecular interactive networks | Compartments | Continuous/discrete time steps |
Graphical model | [26-28] |
| Statecharts & DEVS |
Discrete event system specification | Distinction between system and environment |
Continuous/discrete time steps |
Atomic models and coupled models |
[32,33] |
| Smoldyn | Atomistic modeling of biological processes with dynamic membrane geometry |
Off lattice | Inter-particle collisions |
MD based | http://genomics.lbl.gov/Sandrews/ software.html |
| CyberCell | Atomistic modeling of biological processes with dynamic membrane geometry |
Off lattice | Inter-particle collisions |
MD based | http://projectcybercell.ca |
| MesoRD | Stochastic domain | Compartments, sub volumes |
Event-driven | CME | http://mesord.sourgeforge.net |
| Our Simulator | Stochastic modeling of discrete events | Compartmental | Event driven discrete time steps |
Based on CME, explicit models |
Event-time distributions drive the simulation |
Table 1: Taxonomy of modeling and simulation software for biological systems.
Another technique in building abstract computational models for biosimulation has been developed based on Petri nets [26-28] and stochastic process algebra [29-31]. These methods present a mathematical formalism for representing biochemical pathways within and between cells. In [27], the authors present a stochastic Petri net (SPN) model for studying simple chemical reactions (SPN model of ColE1 plasmid replication) and show how existing softwares can be used to perform structural analysis based on numerical techniques. Discrete event system specifications based on Devs & StateCharts [32,33] and Stochastic Π calculus [31] have been successfully demonstrated to provide a computational platform for temporal simulation of complex biological systems. Hillston et. al have developed a mathematical technique, Performance Evaluation Process Algebra (PEPA) [29,34], wherein functionality is captured at the level of pathways rather than molecules and the system is represented as a continuous time Markov chain.
Other simulation methodologies, based on object oriented and agent based (ABM) paradigms have also been studied for in silico modeling of complex bio-processes by Uhramacher et.al [35-37]. In [38], the authors have developed AgentCell, an ABM based digital assay for the study of bacterial chemotaxis. Another modeling technique, Functional Unit Representation Model (FURM) [39,40] has been proposed for large scale modeling of in vitro drug metabolism. Simulation platforms, based on discrete events, where the events are modeled on rate constants and measured experimental data, have been demonstrated in [12] and [41].
The overarching theme, guiding the development of in silico modeling and simulation tools, is developing models based on continuous-deterministic ODEs or using stochastic simulation algorithms (SSA) for approximating the chemical master equation, which capture the temporal evolution of the biological process dynamics. Most of these techniques focus on molecular pathways, which are represented in graphical and mathematical formalisms, treat spatial dynamics in terms of well-defined cellular compartments and abstract the complexity in terms of estimated parameters and rate constants. Table 1 presents a brief taxonomy of the modeling techniques in terms of these key characteristics.
In the next section, we outline our modeling and simulation technique, based on a discrete event system specification, where the molecular events (representing reactions, ionic diffusions) are mechanistically modeled depending on their biophysical characteristics to compute the probability distribution of their execution times. A discrete event simulation system then links the biological processes to simulate the behavior emerging from the interaction of the events in time.
Modeling and Simulation Approach
A fundamental challenge in computational systems biology [3] is the simplification of the biological system complexity without losing the ensemble dynamic behavior. In the system engineering view of complex processes [42], the key notion is to abstract the complexity of the system as a set of discrete time and space variables (random variables), which capture the behavior of the system in time. The entire system is a collection of functional blocks or modules, which are driven by a set of “events”, where an “event” defines a large number of micro level state transitions between a set of state variables accomplished within the event execution time. The underlying assumption driving this abstraction is the segregation of the complete state space into such disjoint sets of independent events which can be executed simultaneously without any interaction. The application of this technique in large complex communication networks has demonstrated the accuracy of the approach for the first and higher order dynamics of the system within the limits of input data and state partitioning algorithms [43]. For example, discrete event based system modeling has been effectively applied for designing routers, the key components responsible for routing traffic through the Internet. Discrete event based simulation techniques have also been used in a wide variety of manufacturing processes and studying the system dynamics of complex industrial processes.
Motivated by the success of discrete event driven stochastic simulation techniques in large scale complex networks, our approach is based on identifying and modeling key biological functions at a cell, tissue or organ level and mapping those to a set of discrete molecular events associated with the modular processes. Each event represents a molecular interaction (chemical reaction, ionic diffusion etc.) and is associated with two characteristics:
(i) The parametric stochastic model of the underlying physicochemical process associated with the event. The model, elucidated further in the next section, characterizes the holding time distribution associated with the event
(ii) The molecular resources associated with the event (e.g the molecular species involved in a reaction event) and their utilization algorithm based on reaction stoichiometry.
Thus, to define the discrete events, we first identify a biological process as a system of resources (which can typically be the various molecules, ions, ribosome, chromosome, operons, tissue, organ etc involved in the system) that are periodically changing their state between “busy” (e.g., a molecule is busy in a reaction) “free”(e.g., a molecule is free to enter a new reaction) “created” (e.g., a molecule is created by a reaction) and “killed” (e.g., a molecule is taken up by a reaction) based on the underlying resource usage algorithms. The events are marked by the instants the selected resources change their state in the system. The state transitions from one state to another are governed by transition flow rates of the functions involved in the process. The estimation of the transition flow rates is derived by mathematical model or by experimental observation of the physical processes involved in the functions. As an example, we consider the fundamental function of phosphorylation, which involves the transfer of a phosphate ion from an Adenosine triphosphate (ATP) molecule to another molecule/ion resulting in the phosphorylated molecule/ ion and a molecule of Adenosine diphosphate (ADP). In particular, we consider the phosphorylation of a PhoP molecule (which as we will see later is an intra membrane protein signaling molecule involved in the regulation of the PhoPQ pathway in Salmonella) to phosphorylated PhoP or PhoPp. In order to capture the dynamics of this basic biological function, we need to account for the state of the resources involved (in this case ATP, count of PhoP molecule and phosphorylated PhoP molecule, and ADP). Further, the time required to perform this function, which is termed as the “holding time”, is estimated on models based on fundamental physical processes like molecular kinetics, diffusion physics and molecule binding mechanism that will be in place at that particular system state. Thus, this holding time will be randomly changing as the system states change and will accurately reflect the actual working of the cellular system. At the end of the “holding time”, the phosphorylation molecule can trigger an “event” to drive another functional process. As the simulation proceeds at a molecular level, the resource states are determined in terms of the “molecular count” of the individual resources. For example, after the successful completion of the PhoP-phosphorylation function, the count of ATP in the system is decreased by one while that of ADP is increased by one. The PhoP molecule is “killed” and phosphorylated PhoP molecule is “created.” In this way, basic biological molecules and their events are identified, modeled and linked together in a discrete event simulation framework to capture the dy-namic interactions of a cellular process in time.
As is evident from the above discussion, one of the key challenges of this discrete event modeling of biological processes is the identification of basic functional modules [3], the resources involved in them and the key events driving the interaction between the different modules. The wide variability and complexity of modules, resources and possible set of events in natural sciences further complicate the problem. However, there exists a core set of basic functional modules which play fundamental roles in a wide variety of biological processes. Identification and modeling of these functions can greatly facilitate the study of complex processes of life. Some of the basic bio-molecular events, which are associated with key biological functions, include:
(1) Reaction Time
(2) Diffusion Time
(3) DNA Protein binding time
(4) Transcription Time
(5) Translation Time
(6) Transport Time
(7) Protein Life Time
(8) Protein Folding Time
The development of stochastic event models is closely linked to the success of the simulation and forms a central part of our modeling and simulation approach, the basic steps of which are outlined in Table 2. A large volume of work in stochastic in silico analysis of biological systems is centered on Stochastic Simulation Algorithms (SSA) using Gillespie’s technique [19,20] and its variants [21]. While the fundamental notion of approximating the Chemical Master Equation (CME) forms the driving principle in any stochastic modeling framework, the event modeling and execution phase (Step 2 in Table 2) and the resource update phase (Step. 3) differentiates the two techniques. While Gillespie and other SSA algorithms employ a Monte Carlo step to determine the next reaction event and the time-step update, individual event holding time probability distributions govern event time (i.e. reaction time) in our approach and the time-step updated according to the particular random number instantiating the distribution. Such an approach allows modeling different blocks at different levels of granularity depending on available knowledge, allowing one to study the different functional modules of a biological process.
| Stochastic Simulation (Gillespie Algorithm) | Stochastic modeling based Discrete event simulation (iSimBioSys) | Coments | |
| 1 | nitialization: Initialize the number of molecules in the system, reactions constants, and random number generators | Initialization: Initialize the number of molecules in the system for each species, model parameters and resources and random number generators | The initialization steps are similar in both the algorithms |
| 2 | Monte Carlo Step: Generate random numbers to determine the next reaction to occur as well as the time interval. | Event modeling and execution: The next reaction or molecular event is selected based on the functional logic hardwired in the simulator. For each process and its associated event, a random number is generated for the event execution time based on the first and second moment of the event holding time distribution computed by the stochastic model. | In this step, Gillespie and other stochastic simulation algorithms employ a Monte Carlo step to determine next reaction event and time while in our approach, the next event selection and random execution time generation are computed differently. |
| 3 | Update: Increase the time step by the randomly generated time in step 1. Update the molecule count based on the reaction that occurred. | Update: The global simulation clock is increased by the time-step computed in the previous step as the event holding time, The resource count of molecules are updated based on the last event stochiometry | The temporal progression takes place in discrete time-steps based on the random event holding times computed in the previous step in our approach. |
| 4 | Iterate: Go back to Step 1 unless the number of reactants is zero or the simulation time has been exceeded. | Iterate: Go back to Step 1 and repeat the process. In case a particular event cannot be executed because of resource conflicts, it is ignored and simulation proceeds without the update step | The handling of reactions/events with resource conflicts/shortage is different in our approach |
Table 2: Comparison of SSA and iSimBioSys modeling framework.
Tracing temporal dynamics
In the stochastic event-based modeling and simulation approach, the complexity of the system is captured in the “time” domain. The dynamics of resource utilizations with progression in time unveil the complete internal picture of a complex biological process, capturing the evolution of the system in time. In discrete event simulation, “simulation time” is the representation of the “physical time” of the system being modeled. Each event computation is associated a timestamp indicating when that event occurs in the physical system being simulated. As mentioned in the previous section, the event time computation includes the physical function execution time of the system at the current context of the system. This execution time is often called “holding time” of the event function and is generally a random number. The exercise of characterizing the system parameters is performed as follows:
1. Identify the list of discrete events that can be included in the model based on the available knowledge of the system.
2. Identify the resources of interest for the experiment which are being used by the biological process for each discrete event. In other words, we need to identify the various types of molecules, cells, tissues etc which are involved in the resource usage algorithm for an event (either in reactions, or as catalysts or end products)
3. Compute the time taken to complete this biological discrete event, i.e. the holding time of the discrete event. For this purpose, it is important to identify the parameters which affect the interaction of the resources in a particular biological discrete event process and mapping them into time domain. Unlike in rate based simulation models, where it is assumed that the system state remains the same during the complete reaction of multiple molecules, the time required for completion of a biological discrete event processing is computed as a function of these parameters.
Identify the next set of biological discrete events initiated on the completion of an event. If multiple dis-crete events are generated, it is necessary to find out the probability of the individual next event. This modeling of the probability depends on the biological intelligence captured through micro array or other experimental data that are reported in pathway and other research databases. Thus extraction of the system intelligence from the experimental data from PubMed [2] publications to generate the pathway logic is an important component of this modeling technique.
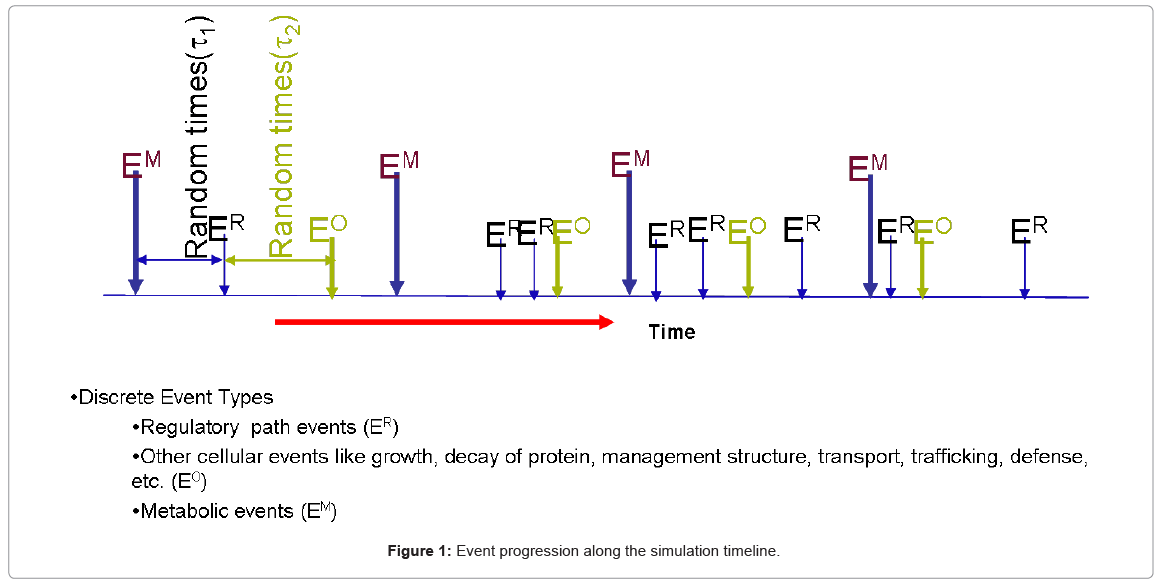
The resource utilization algorithms which determine the holding time of the functional blocks, together with the resources involved and their count in the system, all play a key role in the dynamic behavior of the biological process being simulated. Once the components are defined and linked in the simulation framework, the dynamics unfold by the interaction of different events in time, as depicted in a timeline snapshot in Figure 1.
In summary, our modeling and simulation technique presents a stochastic, event-driven, discrete time-step framework which approximates the stochastic dynamics of the chemical master equation by parametric models of bio-molecular event time distributions. In the next section, we present the simulation methodology, building its different components based on a case study of the virulence gene regulatory pathway in Salmonella.
Systems and Methods
In this section, we present a systematic outline of the methodology of developing the discrete event simulation, presenting the core components involved in building an in silico model of a biological process. The components are built around the case study system, the regulation of virulence gene in Salmonella, specifically the effect of external magnesium concentration on the two component PhoPQ virulence gene regulatory pathway. Building on the case study system, we outline the modeling methodology, mathematical abstraction and the discrete event simulation implementation of the abstraction We start with a brief description of the signal transduction and gene regulation process for this particular two-component system based on available biological literature [44].
Virulence gene regulation in salmonella typhimurium
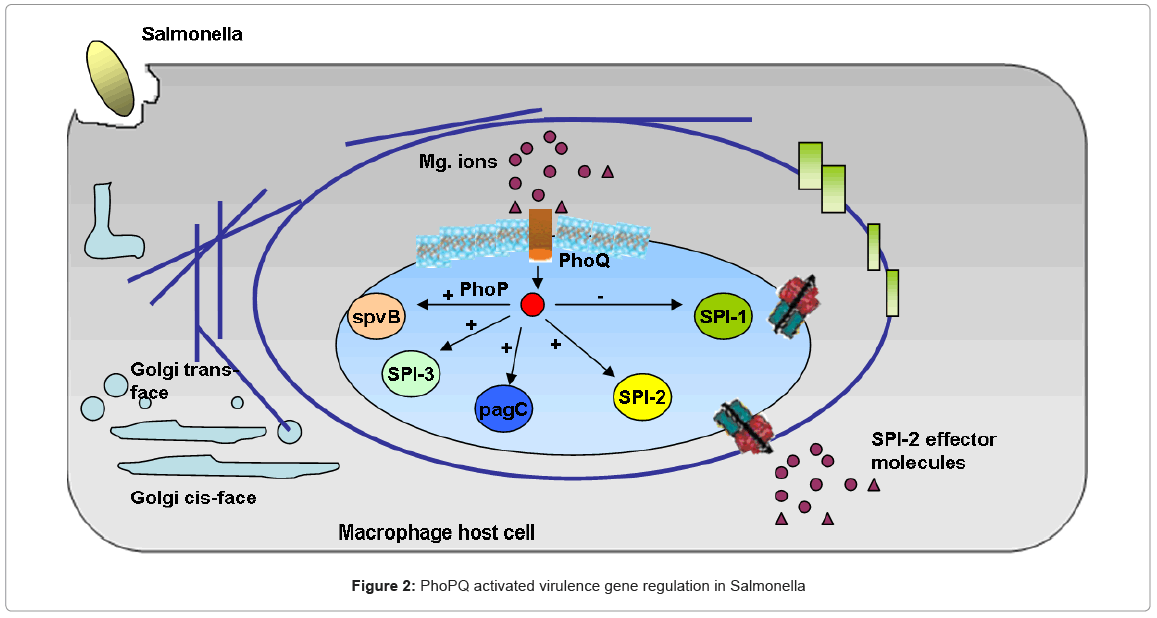
Bacterial pathogenesis in Salmonella Typhimurium involves the complex interaction of regulatory pathways which play different roles in various stages of infection [44]. As mentioned earlier, we focus on the two component phoPQ regulatory system and its role in accomplishing parasitism of the host, [44] elucidates the role of extra cellular Magnesium (Mg+2) concentration as a primary signal of this pathway which acts as a global regulator of Salmonella virulence and helps in the survival and replication of the bacteria in the macrophages, shown in Figure 2 Low extra cellular Mg+2 (microMolar concentrations) was shown to cause an increase in the expression of certain phoPQ activated genes, while high Mg+2 concentrations (milliMolar) caused an immediate “switch off” of these genes. Detailed in vivo and in vitro results for virulence gene regulation in Salmonella are also available [44]. The knowledge available from the biological studies, together with the qualitative diagram of the system in Figure 2 represents the biological process under study.
Modeling methodology
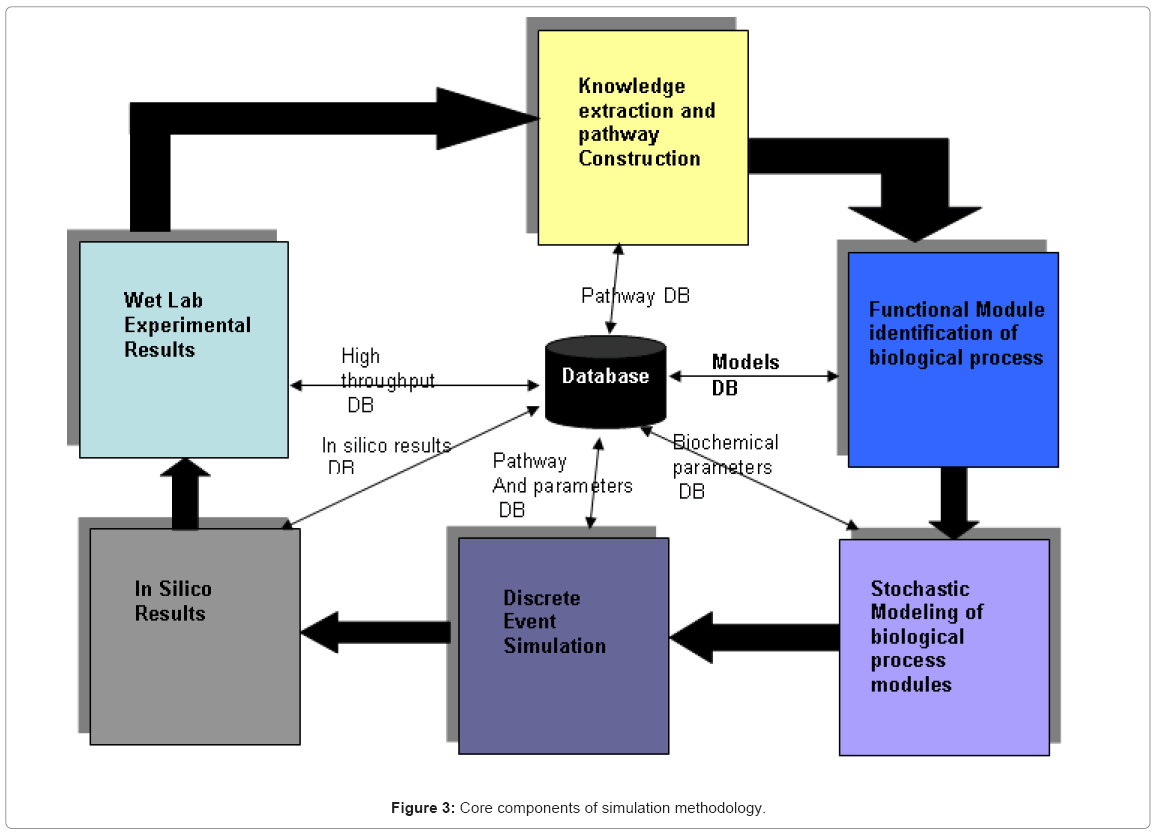
Once the biological knowledge has been defined, the modeling methodology involves 6 components which translate the qualitative knowledge into a quantitative formalism which lends itself amenable to computational study, which is represented in Figure 3.
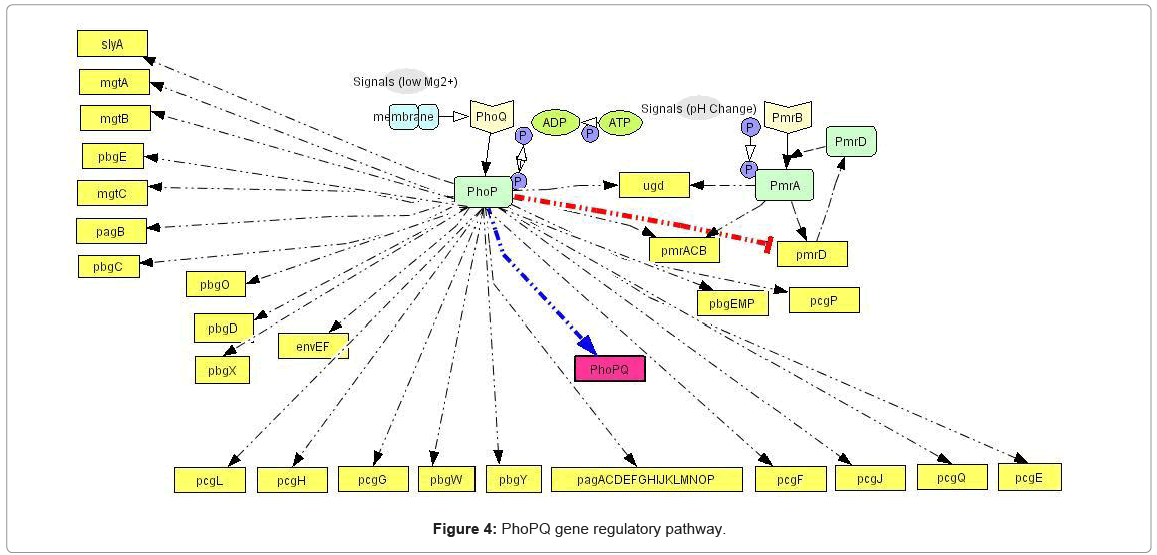
Knowledge extraction and pathway construction: The extraction of current biological knowledge of a given process, with subsequent construction of molecular pathways is the first step in the methodology. We used comprehensive knowledge extraction from PubMed [2] database, to construct the gene regulatory pathways for the phoPQ network, identifying the common intersection of the pathways i.e. the genes and gene products which are regulated by this system at various stages. In our current work, the two component pathway involves transcriptional regulation of 44 genes, 5 of which are involved in another cascading two component system (pmrBA). A positive feedback loop exists in this pathway, in the form of up regulation of phoPQ gene by the system. Figure 4 shows the complete pathway, with the positive feedback loop marked in deep color. The pathways have been constructed using Cell Designer 3.0 which presents a structured (Extensible Markup Language (XML)) format for the data that can be easily rendered into the discrete event simulation framework. The process involved 112 experimental reports of this system that were manually curated from PubMed [2], development of the pathway graphs for each experiment and then concatenating those graphs to get the complete pathway graph. The manual pathway curation involved as a starting point the 10 genes (as shown in Table 5) identified in [55] as phoP associated in the host cell by comparing the expression of human monocytic tissue culture cells infected with wild type and phoP:Tn10 mutant strain.
| Gene name as in the PhoPQ Network | Alias Name | Description | Reference (Locus link ID) |
|---|---|---|---|
| CD9 | BA2, MIC3, P24 | CD9 antigen (p24) | 928 |
| CTSD | CPSD, MGC2311, Cathepsin-D pre -proprotien |
Cathepsin-D (lysosomal aspartyl protease) |
1509 |
| LILRB2 | ILT4, LIR2, MIR-10 | Leukocyte immunoglobulin-like receptor, subfamily B (with TM and ITIM domains), member 2 |
10288 |
| ELF1 | E74-like factor 1, Elf-1, ETS-related transcription factor Elf-1 |
E74-like factor 1 (ets domain transcription factor) |
1997 |
| CISH | SSI-3, CIS, CIS-1 | Cytokine inducible SH2-containing protein |
1154 |
| TNF | DIF, TNFA, TNFSF2 | Tumor necrosis factor (TNF superfamily, member 2) |
7124 |
| PIM1 | PIM, Oncogene PIM1, pim-1 oncogeneg | pim-1 oncogene | 5292 |
| MYB | C-myb, Myb proto-oncogene protein, transforming protein myb, splice form containing exon 9A |
v-myb myeloblastosis viral oncogene homolog (avian)f |
4602 |
| DHFR | DHFR, dihydrofolate reductase | Dihydrofolate reductase | 1719 |
| CDKN1B | KIP1, P27KIP1, CDKN4 | Cyclin-dependent kinase inhibitor 1B (p27, Kip1) |
1027 |
Table 5: List of genes used to construct the PhoPQ regulatory network (Figure 4) that were identified as phoP associated in the host cell in [44,55].
The gene regulatory pathway facilitates the first stage of our system modeling approach and is responsible for driving the complex dynamics of the biological process of PhoPQ system. It leads to the identification of the various “resources” involved in the system, whose ensemble dynamics in time drive the system output. Figure 4 marks the first step in the transition of the qualitative knowledge of the biological system (as captured in Figure 2) into a computational format captured in the pathway network structure.
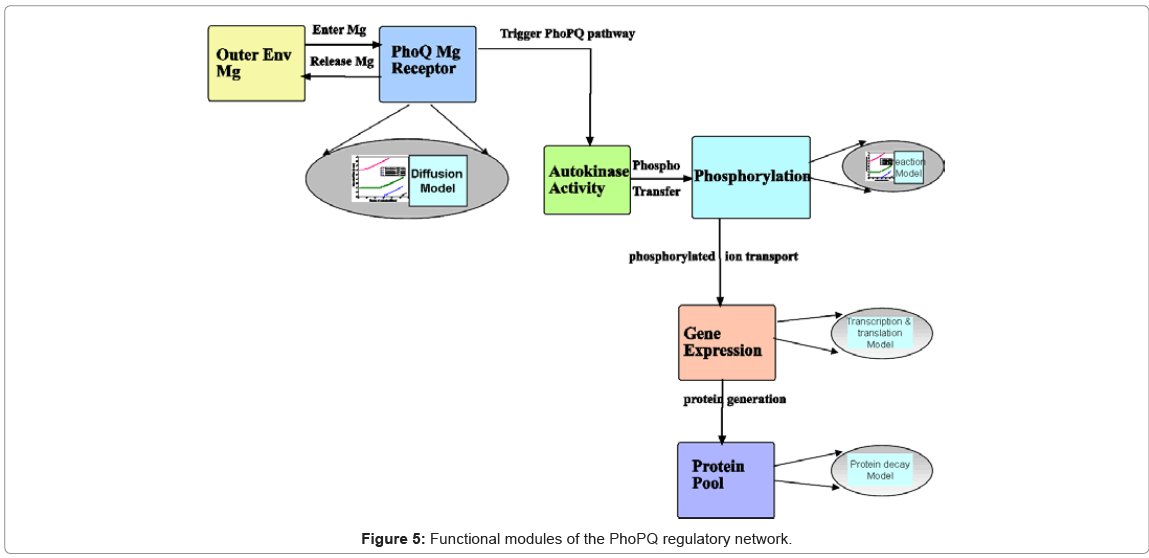
Functional module identification of biological processes: The next step in model building is the abstraction of the biological phenomena which are involved in the system under study. In our case, it translates into the basic processes which are involved in the activation of the PhoPQ system under external magnesium, follows by expression (up regulation) or repression (down regulation) of genes in the pathway. Based on a large body of work available in literature, the main functional modules have been described in Figure 5 The biological process modules identified here are at different levels of granularity. For example, the autokinase activity [44] of PhoQ receptor molecules involves phosphorylation of a single PhoQ molecule. However, gene expression is a complex process, involving a large number of complex sub processes, all of which are not fully understood currently. Thus, the functional modules need to incorporate these varying levels of granularity in their event models, which we illustrate next.
Figure 5 marks the final step in the transition of the biological knowledge into the computational modeling and simulation frameworks, encompassing curated database (Figure 4) together with system model characteristics.
Stochastic Event Modeling: The mathematical formalism underpinning the simulation of the biological processes is the stochastic modeling of the molecular events associated with the processes. As mentioned earlier, the modeling of the event holding time of the functional modules (the arrows between the modules in Figure 5 denote the events), is a key distinguishing step in our methodology. In the discrete event simulation execution, for each process and its associated events, a random number is generated for the event execution time or holding time. This time step drives the dynamics of the simulation and the change in state of system resources. In our approach, the random holding time is generated as an instance of the probability distribution associated with the particular even-t. This parametric distribution, defined in terms of its first and second moments, is computed from the stochastic modeling of the biophysical and biochemical properties of the process (elliptical modules in Figure 5) and forms the heart of the stochastic event modeling step.
As mentioned in the previous section, several key events which together define a functional bioprocess require to be modeled as part of the modeling and simulation procedure. However, the simulation framework is capable of incorporating models in varying degrees of granularity and abstraction, based on available knowledge, empirical and experimental data or on the focus of a particular system. Below, we summarily present our stochastic model formalism for two key processes that were directly used in this paper together with a third model presented at significantly higher abstraction. More details on all the stochastic models that we have developed and validated earlier are available in [45-48,50,56-66].
A. Transfer of magnesium ions through the cell membrane
As the PhoPQ pathway is controlled by extra-cellular magnesium ion concentration, the movement of Mg2+ through the cell membrane needs to be modeled (first two modules in Figure 5). This process is modeled as diffusion of charged ions through the cell membrane
Specifically, the event time for a molecule of Mg2+ entering or leaving the membrane needs to be computed. This deals with the interarrival (departure) time between two molecules or ions, where their movement to/from a cell is controlled by concentration gradient and ion charge potential gradient across the membrane. The inter-arrival (departure) time is controlled by the ion flux in this case. This requires a transient solution whereas existing cell biology models offer only steady state solutions [18,49]. To derive the inter-arrival (departure time between the ith and (i+1)th molecules i.e. ti+1 – ti , we determine tN-i-1 and tN-i that denote respectively the times to transfer and molecules/ ions through the channel, where N is total number of molecules/ions. Now, can be obtained by solving the following equation [45,46,48]:
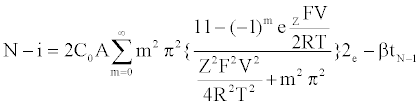 (1)
(1)
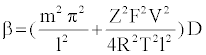 (2)
(2)
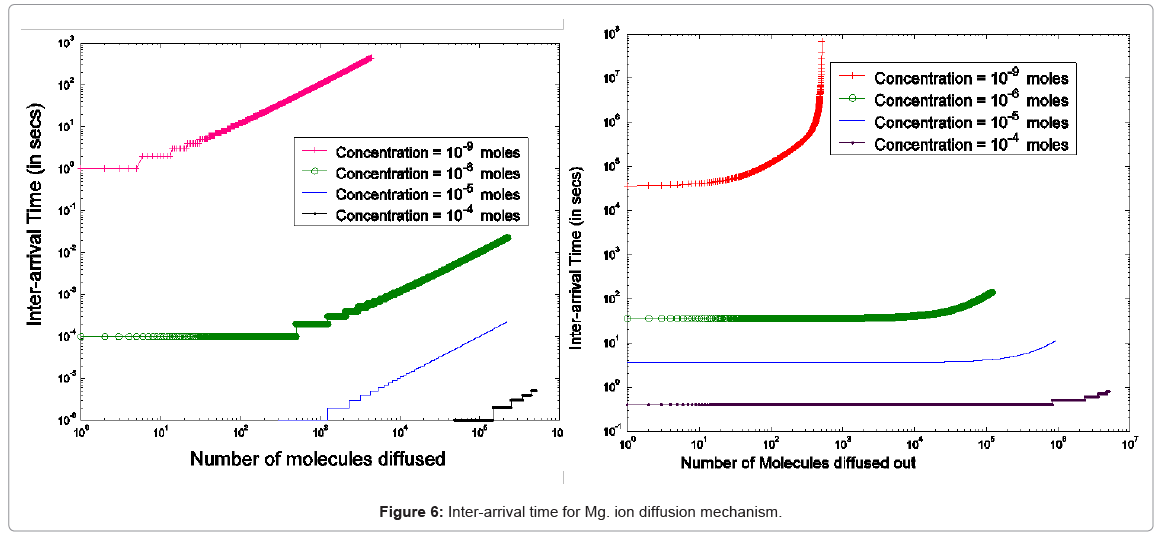
The parameterized equations in (1) and (2) capture the different physico-chemical factors affecting the diffusion of charged ions. Based on the parameter values for diffusion of Mg. ions through the bacterial cell membrane, Figure 6 shows the inter-arrival time for different concentrations of Mg. ions in the extracellular environment.
B. Phosphorylation and other molecular reactions: The process of phosphorylation is considered as a reaction system. Applying collision based reaction rate model coupled with the molecular velocity distributions and free energy parameters of the reaction, two discrete stochastic time models for cytoplasm reactions are derived in [47,50,56,65]. The first model addresses the cytoplasm reaction of a single molecule with a second type of molecular concentration. The average reaction time is Tavg = τ/p and its second moment is T2ndmoment = (2-p) τ2 /p, where p is the reaction probability of the first molecule in the solution during an infinitely small time τ. The above model can be extended to the reaction of a batch of n1 molecules of type X1 with n2 molecules of type X2. At each time step τ of the reaction, fewer molecules of the second type will be free as some of them are already used in the previous time steps. The average and second moment of batch reaction completion time are given by
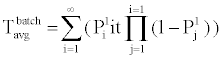 (3)
(3)
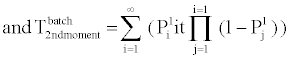 (4)
(4)
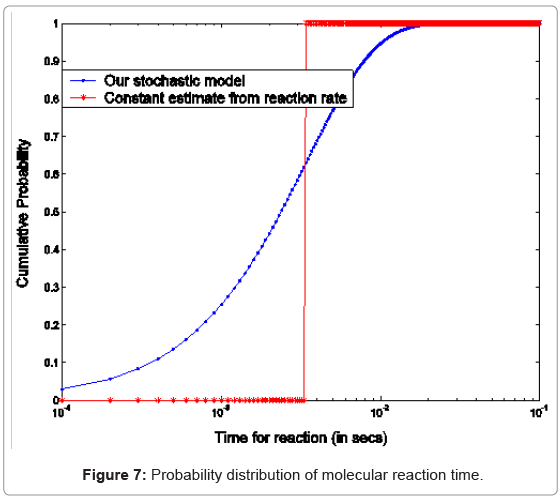
where p1i is the probability of one molecule of type X1 having collision with a molecule of type X2 in the ith time step. Based on the first and second moments computed in Eqn. (3) and (4), it is possible to determine the probability distribution for bi-molecular reactions as shown in Figure 7 where rate-based continuous reaction-time estimates are also compared as having a step probability function of 0 or 1 depending on the reaction time (i.e. 1/reaction rate). These two illustrative cases capture the mathematical formalism of the stochastic models for the bioprocesses which are then utilized by the discrete event simulation for specific functional units associated with a particular system (phosphorylation and auto-kinase reactions and Mg. ion diffusions in the PhoPQ pathway test-bed studied in this work).
C. Gene expression modules: As a final illustrative case, we focus on the complex module of gene expression and protein synthesis which orchestrate the expression dynamics of the different genes involved in a particular gene regulatory pathway. The stochastic nature of gene expression and the multitude of factors both at transcription (RNA polymerase copy number), translation (competition between ribosome and RNaseE molecule for translation initiation or decay respectively) as well as posttranslational stages pose modeling challenges in this complex molecular assembly phage, particularly in the light of knowledge gaps in the biological understanding of various parts of the process. As our framework is capable of encapsulating such knowledge gaps through high-level abstractions, in our current work, the holding time in these blocks have been essentially based on existing experimental data, collected for average bacterial transcription time and translation times (Table 3). The complex process of protein formation and decay have been modeled as an exponential distribution with the exponent computed as a function of the number of proteins in the system and its half life values, which depends on the conformation and residue length of a particular protein obtained from the PubMed and EcoCyc databases [51]. While such modules at varying degree of model granularity can co-exist in our framework, proper estimation of parameters (from in vivo and in vitro data) can increase the efficacy of the model. Once the bioprocess events are modeled, the discrete event simulation can link these events and their execution times to unfold the temporal dynamics of the system.
| Biological Parameter (Bacteria) | Value | |
| 1 | Length of genome | 4857432 |
| 2 | Number of genes | 4451 |
| 3 | Rate of transcription | 50 nucleotides/sec |
| 4 | Rate of Translation | 18 residues/sec |
| 5 | Area of cell | 6*10-12 sq.m |
| 6 | Volume of Cell | 1*10-15 L |
| 7 | Diffusion co-efficient of magnesium ion | 1*10-9 |
| 8 | Diffusion co-efficient of a protein molecule | 7.7*10-6 |
| 9 | Avg. mass of a protein molecule | 25kDa |
| 10 | Avg. diameter of a avg. protein molecule | 5 nm |
| 11 | Millimolar conc. of Mg | 1.0*10-3 |
| 12 | Micromolar conc. of Mg | 8.0*10-6 |
| 13 | Phosphorylation Reaction Time | 5.6*10-9/ (No. Of reactant molecules) secs |
| 14 | Avg. delay between diffusion of two mg molecules | 8.5*10-10 secs |
Table 3: System model and simulation parameters
Discrete event simulation: This is the heart of the framework, comprising of the core simulation engine responsible for driving the system in silico. Based on the functional modules elucidated in Section 4.2.2, the key events driving the interaction of these modules are identified, as shown in Figure 5. The event times associated with each of these biological events are developed based on the stochastic modeling techniques outlined in Section 4.2.3. The discrete event platform incorporates this information in its framework, the details of which are outlined in Section 5.
In silico result and wet lab verification: The success of the simulation methodology depends on the validation of results with wet lab experiments. This provides a tool for in silico verification of biological processes and for subsequent hypothesis testing of biological functions prior to more advance and costly in vitro and in vivo experiments. In Section 6, we study the validation of our test bed system against experiments performed in [44].
The six components elucidated in this section, powered by large databases of molecular knowledge, iteratively interact to form an in silico modeling and simulation platform.
iSimBioSys software Architecture In this section, we develop the software implementation of our discrete event simulation platform, iSimBioSys, based on the methodology explained in the previous section. The modular nature of the functional blocks involved in a system engineering approach lends itself to an object-oriented computing paradigm [35,36]. Specifically, the Java based [52] implementation encapsulates the stochastic models for the different molecular events and links them together in the discrete event simulator.
Each functional module is represented as an object, having its own state (the resources involved in the module) and its associated behavior, which is modeled on the functionality of the module. Another characteristic of a module are its associated input events, which drive the functionality of that module and its corresponding output events which are inputs to other modules. The central theme of a discrete event simulator revolves around the event queue, which is the global data structure responsible for storing time-stamped events for the simulation. The event queue maintains an event list containing the events to be executed. Instead of having each event store its corresponding execution time as done in [12], each event is associated with the corresponding model object (an instance of a model class) which stores the first and second moment of the probability distribution associated with the event, e.g. the diffusion event is associated with the mean and variance of the probability distribution as computed in the model formalism outlined in the previous section. A central scheduler is in control of the queue, popping events in a time-ordered manner to avoid “causal errors” [12] and sending it to the corresponding modules. At each event triggered, an instance of a random variable following the corresponding probability distribution is computed to calculate the event execution time for the particular molecular event. Based on the event execution logic, new events are created and pushed into the event list, updating the global simulation clock in the process. The scheduler is also responsible for maintaining the event list as events are generated by a module following its biological process logic. As is evident from the discussion, the scheduler together with the event queue drive the simulation environment while the module objects and their behaviors define the event handlers of the framework.
Our current framework supports a multi-threaded architecture with the main simulation engine running in one thread while the visualization plane running on another. The basic architecture and framework of the simulation involves four logical packages as follows:
• In Silico experimental setup: These set of classes are responsible for setting up the modeling and system parameters used in the particular simulation block and are generally provided through user interface or plain text files. While certain parameters are based on available biological literature such as cell volume, macro-molecule diameters etc., event execution time parameters are computed by the engine internally based on the logic defined in the corresponding model class for each event.
• Discrete event process modules: These set of classes, derived from a common base class, essentially the resource utilization algorithms for the biological process being simulated and provide methods to compute event holding times. It may be noted here that the discrete event process modules are a oneto- one mapped implementation of the functional modules identified in Figure 5 These event modules act on the system resources constructed in the knowledge extraction phase. In our current implementation, the resources are modeled in a two dimensional data structure consisting of the resource state and its regulation logic (up or down regulation) based on the constructed pathway. As the event modules run in time, the resource states change and capture the dynamics of the system. These set of classes form the heart of the modeling formalism as they realize the stochastic behavior associated with each molecular event in terms of its probability distribution
• Main simulation engine: This class is responsible for handling the main thread of the discrete event simulator and implements the global event queue used. This class is responsible for communicating with the global event queue through the scheduler, executing the event process logic, updating the global simulation clock and exchanging resource state information with the visualization unit which updates the system behavior in real-time.
• Visualization and data generation: These set of classes are responsible for data generation of the simulation and tracing the simulation in terms of change in resource states in the temporal axis
User interface
The user interface of the current implementation involved three parts:
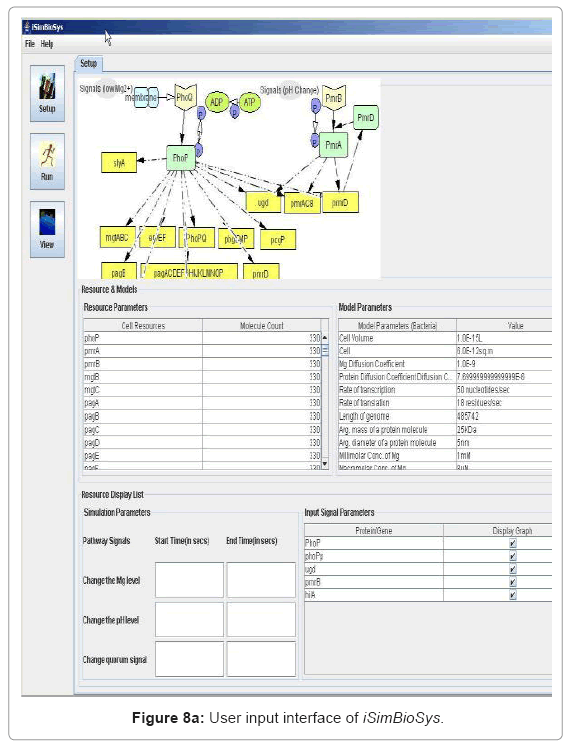
• User Interface for experiment setup: The user interface is presented before the start of the simulation for the user to set up system parameters, simulation runtime environments and visualization data. Figure 8(a) captures snapshot of this interface.
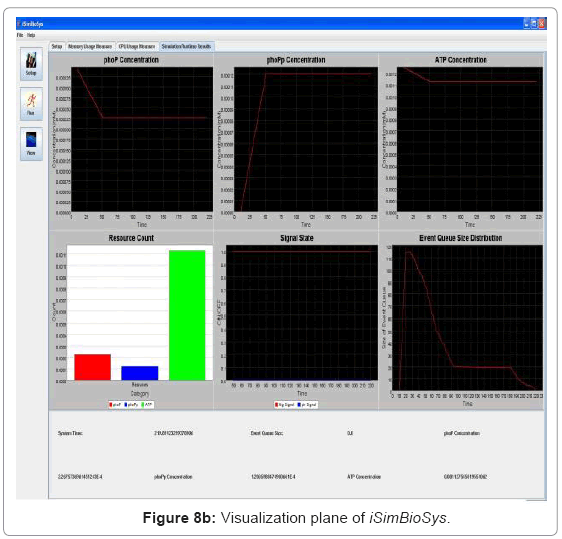
• Runtime visualization of simulation: The simulation can be traced in run-time in the visualization plane which runs on a separate thread as discussed earlier. Depending on user inputs, it traces the change in resource concentration of the system and also system signal states. As the dynamics of the system are traced in time, it provides a window for viewing the system behavior while the simulation runs in the background. Figure 8(b) captures the visualization frame.
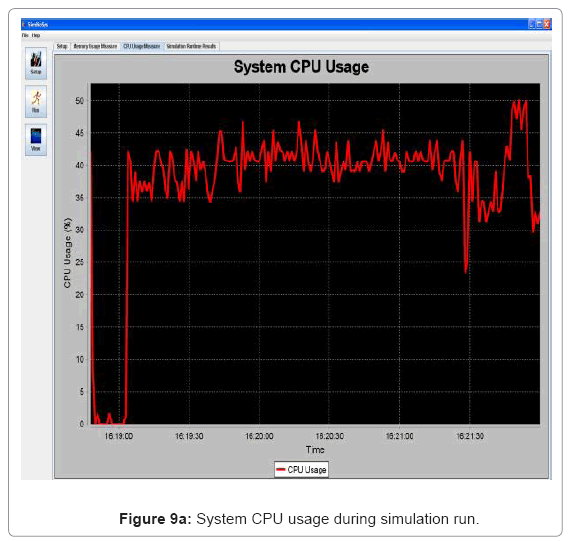
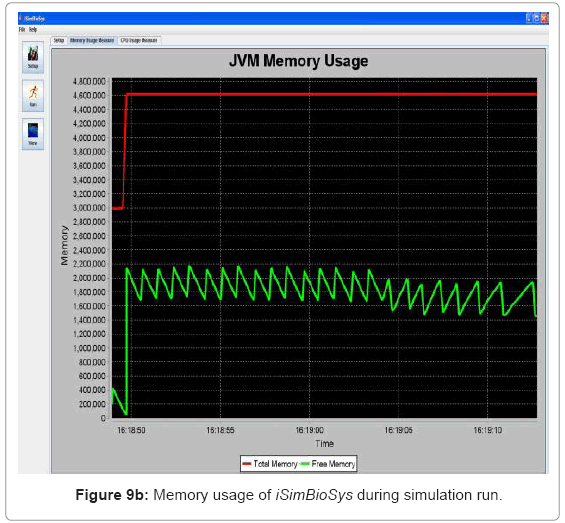
• Performance visualization: These screens trace the various performance metrics of the simulation platform as it is executed. In the current implementation, it is trace of the memory and CPU usage of the system. Figure 9(a) and Figure 9(b) show the CPU and memory usage system snapshots.
It may be mentioned here that the current implementation of iSimBioSys is based on Java 1.5 SDK and runs on a windows XP service pack 2 (enterprise edition) based Dell XPS Dimension system (Intel Pentium 4 processor with HT technology running at 3.4 GHZ), 2GB DDR2 SDRAM at 533 MHz and 250MB ATI Radeon X850 XT PE video card.
Modeling validation and performance measurement
The efficacy of an in silico modeling and simulation approach is governed by (a) validation of the model against existing wet-lab experimental results, (b) effective calibration and sensitivity analysis of the key parameters governing the biological model and (c) hypothesis testing of different conditions on the biological system which can give further insights for novel experiments in the future.
In this section, we employ the discrete event based stochastic simulation framework to model the dynamics of molecular-level cell dynamics, specifically, the effect of the PhoPQ two-component signal transduction pathway on the expression of virulence genes involved in bacterial pathogenesis of the gram-negative bacteria Salmonella Typhimurium. While the simulation system can be used to model the temporal dynamics of different regulatory pathways in a bacterial cell, we focus on the particular system in this work as it provides,
• Existing wet-lab experimental setup and results [44] which allow the validation of the in silico results
• The system involves the interaction of signal transduction with subsequent expression of genes governed by the upstream signals
• The gene regulation pathway as built based on existing literature on the two-component system provides various regulatory mechanisms including up and down regulation of genes, and positive feedback effects which can serve to test different hypothesis in silico.
• As the system involves complex biological functions like gene regulation and protein expression, whose exact molecular mechanisms are not always well known, it provides a platform to test the efficacy of granular model abstraction based on available knowledge, on the behavior at a systems level.
In the rest of the section, we start with a brief description of the wet lab experimental system, moving on to present the detailed results of in silico analysis. We show how the discrete event simulation framework can be used for hypothesis-driven analysis of different conditions in silico for the PhoPQ system. Also, we quantify the performance metrics of the simulation for this test-bed system and study how the framework behaves in terms of memory usage, CPU usage, event queue size and method call graphs.
The wet lab experimental system
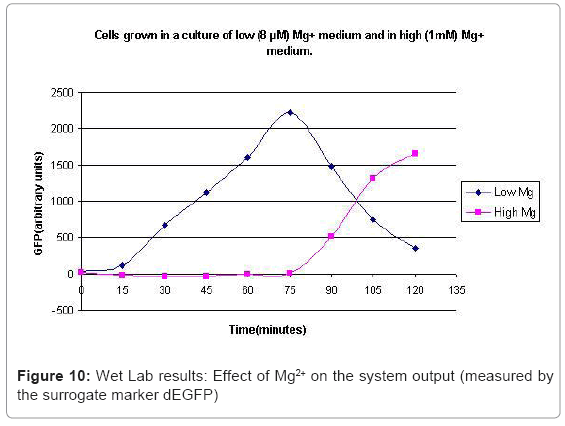
The experimental setup, explained in [44], consists of reporting the system output of the phoPQ system on bacterial cells. Expression of destabilized green fluorescence protein (dEGFP) under the control of a PhoPp (phosphorylated PhoP) responsive promoter was used as the reporter system. The expression of dEGFP was measured as the surrogate output of the system behavior when subjected to various levels of Mg2+ in the growth medium. Initial experiments with two different levels of Mg2+ namely 8 μM (low) and 1 mM (high), suggested that the system behaved similar to a toggle switch. Bacterial cells were grown in two different media: low and high Mg2+ media. After they entered the logarithmic growth phase, the respective growth conditions were switched.
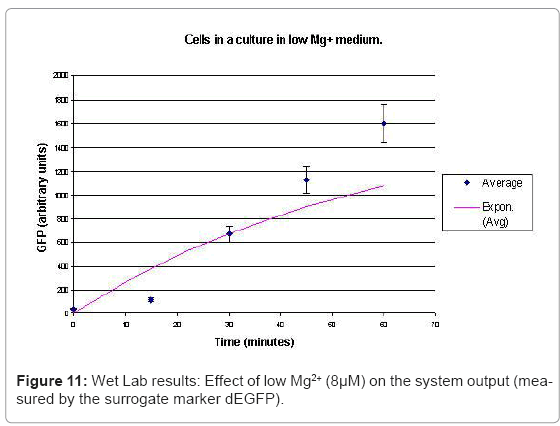
In the experimental system, low Mg2+ was maintained for a period of 60 mins, during which the system output increased, after which the signal was toggled to high Mg2+. The measurements of the fluorometer were taken every 15 mins for the positive activation state. The experiments were repeated thrice and the mean of these three datasets were used for the experimental plots. All measurements were taken when the cells were in the logarithmic growth phase and were corrected for cell density and normalized for cell number. Figure 10 shows the system output of the cell culture in time, both for highmagnesium as well as low-magnesium conditions. Figure 11 shows the system behavior as observed for time of 60mins.
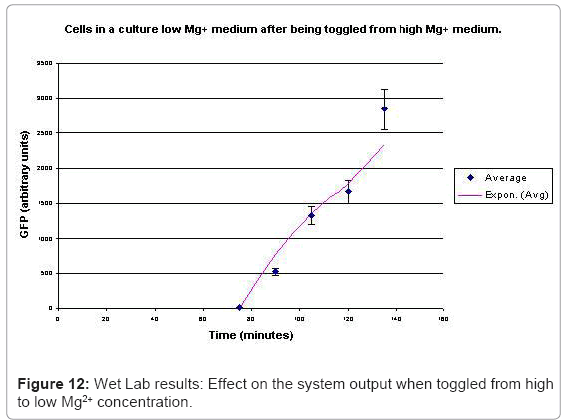
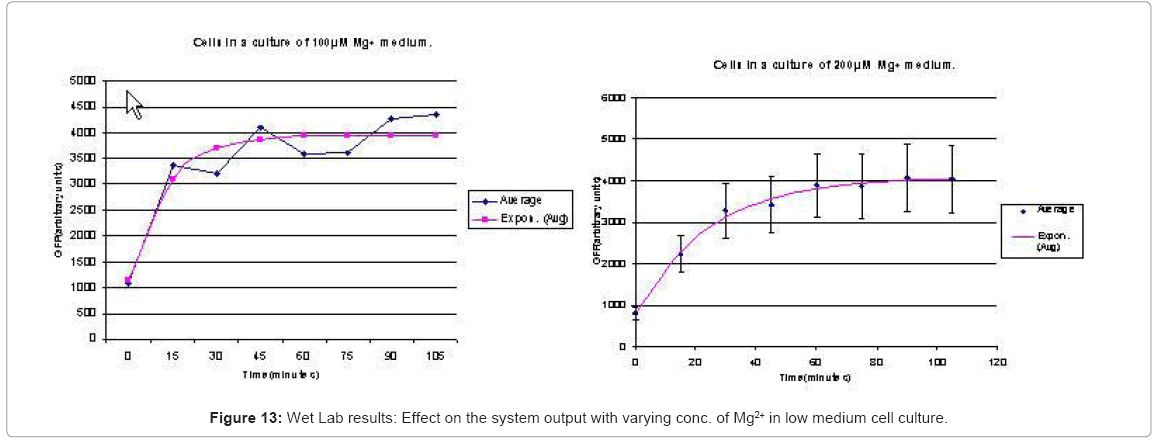
When the cells were in a culture of low (8μM ) magnesium medium. It shows how in low magnesium, the PhoPQ pathway is activated (as shown by increase in concentration of PhoPp). Similarly, Figure 12 shows the toggling effect of the “on-off” switch mechanism when the system state was changed from high to low magnesium medium. Finally, in Figure 13, the effect of varying concentrations of magnesium in a low state (active) are captured for 100μM and 200μM respectively. Based on these experiments, we run the discrete event simulation to generate in silico results which capture the system output in time. The simulation initialization with different resource and system parameters are key to the success of the model. Also, the platform provides flexibility in changing these conditions and resources to generate synthetic, hypothetical results for a better understanding of the test system. In the next subsection, we outline the system and simulation parameters and present the results of the in silico experiment.
In silico validation
In this section, we setup the “dry-lab” experimental system for the signal transduction and subsequent gene regulation pathway involved in the test-bed. The in silico experiment is initialized with the systemmolecular resources and biological parameters associated with the probability distribution functions of the different event holding time modules. In this experiment, we focused on parameters associated with the Salmonella bacteria cell based on the CCDB database [53] which are summarized in Table 3. The simulation also initializes other resource parameters like the number of molecules (in terms of concentration) for the different species involved in the system (e.g. ATP, ADP, PhoP, PhoQ, extracellular Mg. ions) and the gene regulatory pathway information extracted during the PhoPQ pathway creation phase. Once the system is initialized, the event queue is populated with the initial event list which determines the snapshot of the biological environment at simulation start time and the simulation engine is triggered.
For the current system, the simulation focused on tracing the effects of signaling events (Mg. ion arrival and departures) on the expression dynamics of the PhoPQ pathway. Also, as a reporter protein (GFP) has been used in the wet-lab scenario to trace the system behavior, our results are focused primarily on PhoPp as the main resource whose dynamic temporal behavior was observed in the simulation. Although, the simulation can be configured to monitor and generate results for a wide range of system resources, PhoPp was chosen primarily to verify the wet-lab tests. The simulation experimental results denote resource states averaged over 100 runs of the simulation under the same initial conditions.
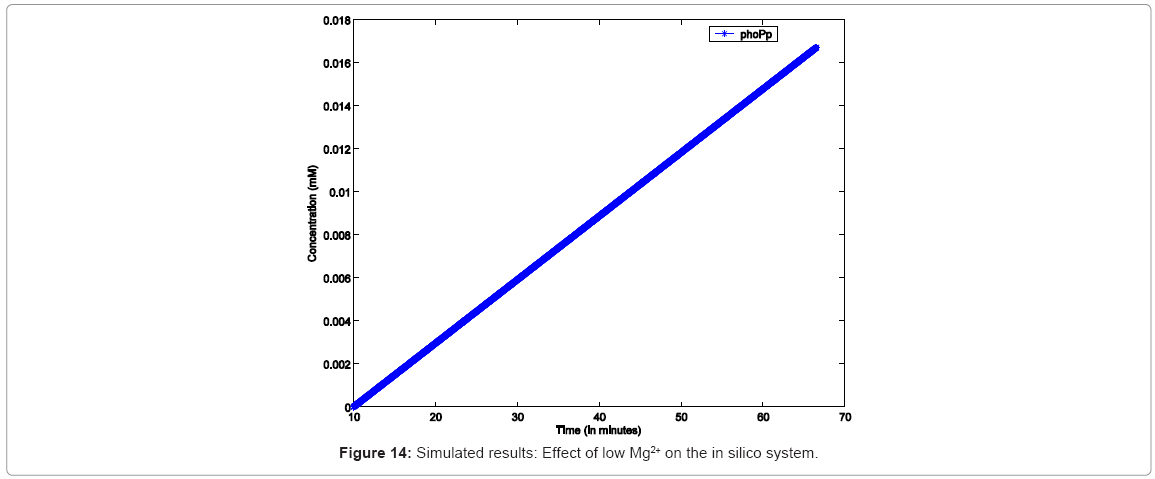
In order to simulate similar conditions “in silico”, the simulation was configured to run with low Mg2+ for 60mins, during which no resource conflicts or starvation were assumed (i.e, the simulation would not stop due to lack of any resource). As seen in Figure 14, the simulation responds with continuous growth in PhoPp concentration, implying increasing dEGFP fluorescence.
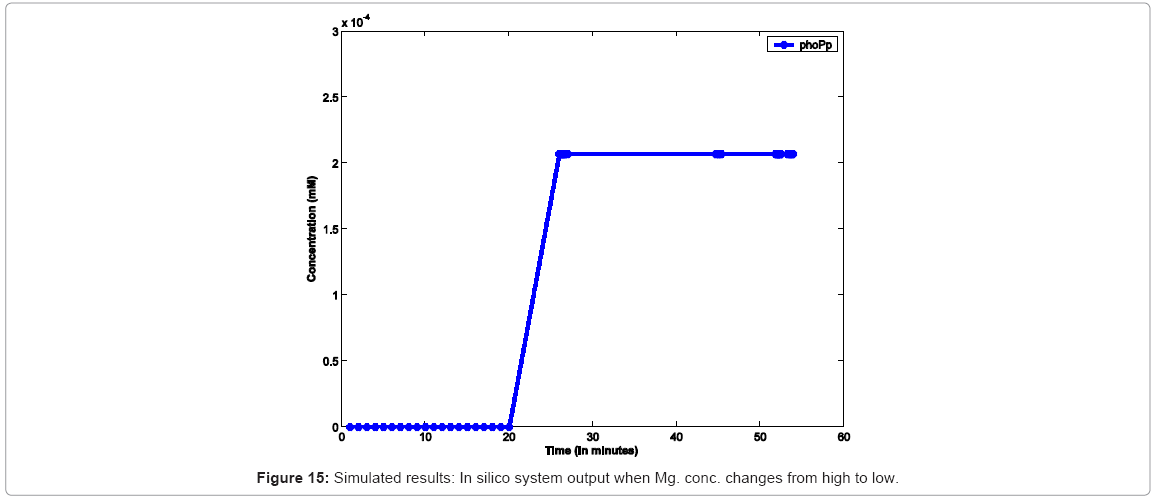
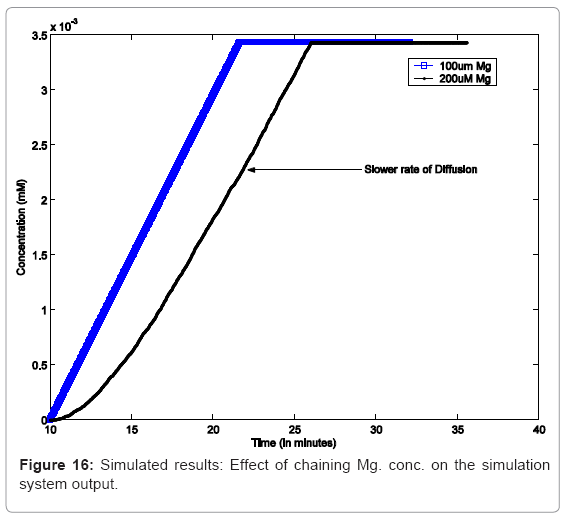
In another simulation experiment, the system was started with high Mg2+ which was switched to low Mg2+ at 20mins which was kept low for 30 mins and toggled back to high. Figure 15 captures the system response under this scenario. In order to study the effect of varying concentrations, as reported, we capture similar conditions in silico in Figure 16, which captures the effect increasing Mg. concentration, leading to decrease in the rate of diffusion of Mg. ions from cell membrane to the environment, thereby causing a decrease in the rate of PhoPp production.
As seen from Figure 15 and Figure 16, the effects capture by the simulation show similar dynamics to the wet-lab system. Also, the condition of no resource starvation shows relative smoothness in output as obtained from continuous system models since the effect of low copy number of molecules on stochasticity [16] is not displayed
The in silico platform allows the a alysis of the effects of stochasticity on the model by varying the resource states of the molecules involved in the simulation and also the sensitivity of the system outputs to the different parameters governing the event holding time distributions. In the next sub-section, we present a systematic analysis of the different in silico hypothesis tests.
In silico hypothesis testing
The in silico simulation model allows the modeler to test the system under various synthetic conditions, in terms of system resource states, initial conditions and different combinations of environmental cues driving the systems (for example, the diffusion of magnesium ions through the cell membrane in our case study).
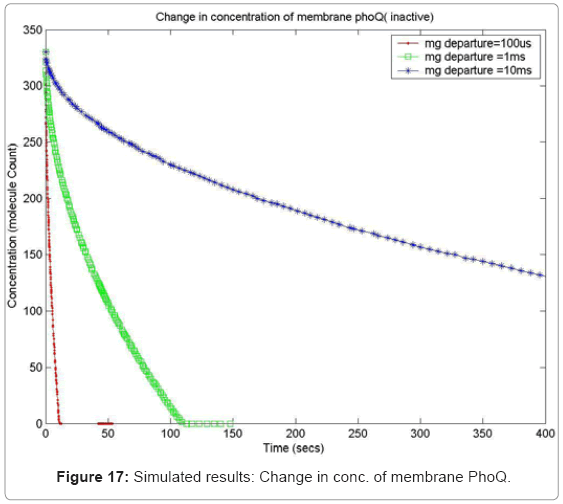
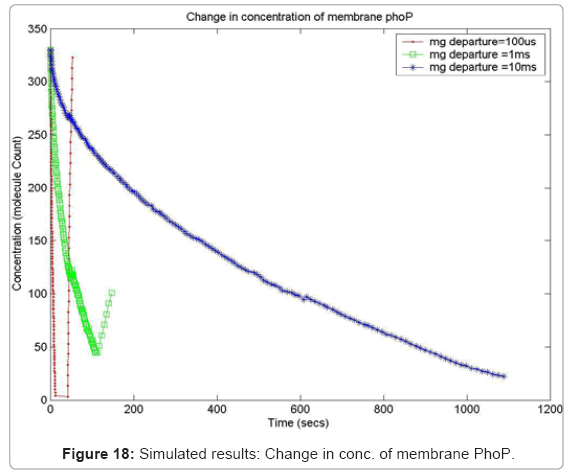
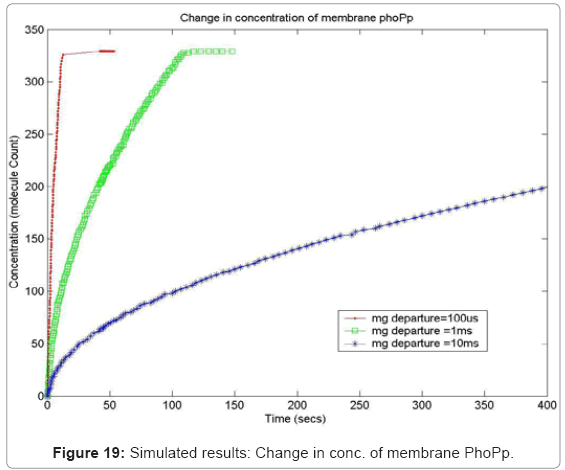
In order to capture the effects of varying the rate of diffusion of magnesium on the system output, we ran the simulation with increasing magnesium ion diffusion times (100ms, 1ms, 10ms) and reported the results for two key system resources, the proteins PhoQ, which is the sensory protein responsible for binding to magnesium ions, and the PhoP protein, which controls the dynamics of the gene expression. Figure 17 shows how the rate of decrease in the concentration of inactive PhoQ (phoQ molecule bound to a magnesium ion) is damped with increasing delay in the diffusion of magnesium ions out of the membrane. Also, capture in this graph is the effect of resource starvation on the biological system. As the Mg. ion initiated signal activates the PhoPQ pathway, the sensory PhoQ proteins are consumed by the system, thereby shutting down the pathway when all phoQ molecules available to the system have been used. Similarly, Figure 18 captures the effect of the same conditions on PhoP. An interesting observation, not capture in the wet-test lab results, is the orchestration of the positive feedback loop of PhoP, as identified in the knowledge extraction phase. As seen in Figure 18, the concentration of PhoP in the system decreases initially; but once, the expression of genes is triggered by phoPp (phosphorylated PhoP), PhoP starts appearing in the system. The corresponding effect on PhoPp, which increases in concentration when magnesium ions depart from the membrane (activating the pathway) is captured in Figure 19. In both the graphs, the slowest rate diffusion does not bring the system into resource shortage phases while the other diffusion rates locks the system (plateau on Figure 19) due to non-availability of phosphorylated PhoP molecules. These graphs show how the tuning of different parameters (in this diffusion rates) can be synthetically manipulated to study different behaviors of the systems.
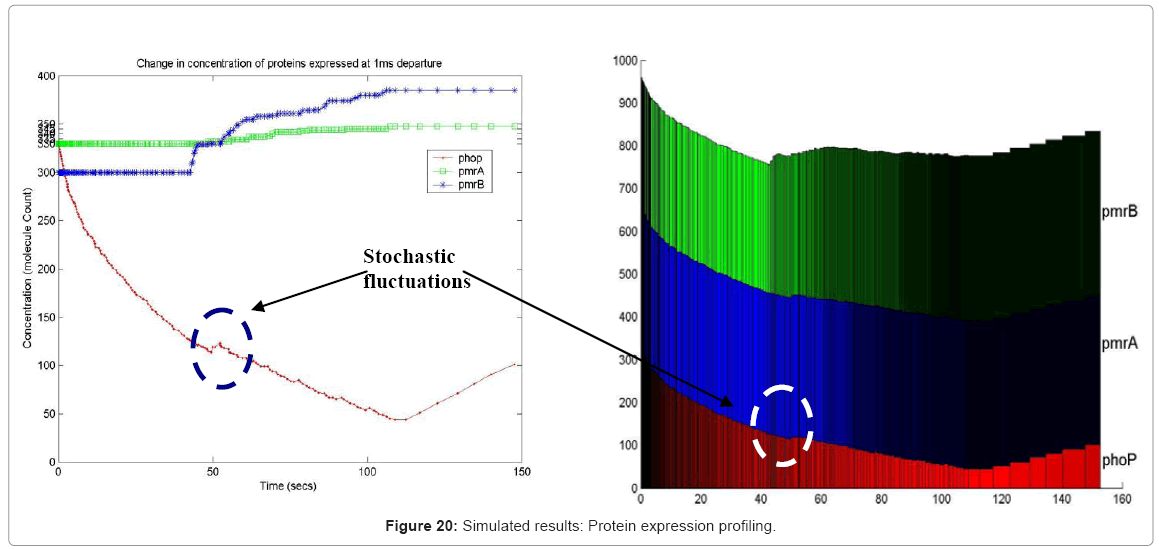
Another in silico result, which is possible in our simulation framework is the profiling of different resources, which though key to the system as a whole, but may not be the focus of a current experiment. For example, it is possible to profile metabolites and energy molecules like ATP and ADP, to name a few. Also, the expression profile of a whole range of gene products, like proteins and enzymes can be traced in the simulation, providing an in silico gene profiling microarray. In Figure 20, we show the color coded protein profile of 3 proteins in our test bed pathway, as they unfold in time. The protein expression profile captures the stochastic fluctuations of the PhoP molecule as the system progresses in time, triggering the positive feedback effect of the phoP gene on the two-component pathway ( as shown in Figure 4).
The in silico results on the test-bed pathway demonstrate the efficacy of the modeling and simulation approach for study celllevel dynamics. Particularly, the flexibility in event scheduling and resource state specifications allows a modeler to validate the effects of high and low copy number of molecules on different parts of the biological system. Moreover, the flexibility allows the simulation to be computationally efficient depending on the required granularity of the biological model and the resource state space considered [54]. In the next section, we present a brief perspective on the computational requirements of our simulation system based on the test-bed cell-level biological experiment.
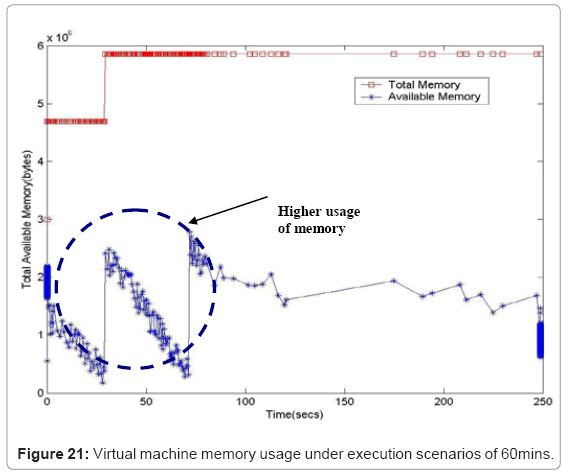
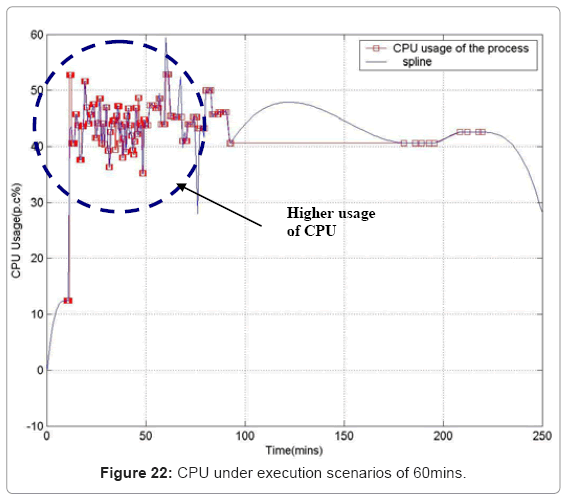
Performance metric of the simulation platform In order to measure the behavior of the simulation software framework, we have developed a memory and CPU usage monitor tool which runs in a parallel thread with the simulation. Considering the scenarios of the in silico experimental setup running for 60min of low magnesium, i.e. when the virulence genes are up regulated, we consider the response of the platform in terms of Java Virtual Machine (JVM) machine usage (total memory and free memory) and CPU usage of the particular process. Figure 21 and Figure 22 show the response to the above mentioned parameters. As can be seen in Figure 21, the simulation engine leads to an increasing usage of memory (decrease in size of free heap memory) as the event queue size increased with more gene expression events generated in the system. Also, it can be noted that as the size of free memory falls below a threshold, the garbage collector agent (gc) of the JVM is invoked which increased allocated memory and increases the size of free heap temporarily before starting to decrease again (the saw-tooth nature of the encircled region in Figure 21). On the same lines, the CPU usage of the process increases around the same region Figure 22). A spline invariant curve has been fitted to the CPU usage data to present a handle on the overall nature of usage by the process. A call graph for the different methods of the simulation was generated at run-time using a run-time java code profiler to capture the distribution of method invocation for the core engine, an analysis of which is presented in Table 4.
| Package | Name | Number of Calls | Cumulative Time | Method Time |
| SimulationEngine | MainEngine.writeFile(String, double, double) | 8,064 | 159,967 (33.6%) | 517 (0.1%) |
| SimulationEngine | MainEngine.startSimulation() | 1 | 290,664 (61.1%) | 82 (0.0%) |
| SimulationEngine | MainEngine.reportResults() | 1,344 | 276,565 (58.1%) | 69 (0.0%) |
| SimulationEngine | MainEngine$1.compare(Object, Object) | 31,611 | 49 (0.0%) | 25 (0.0%) |
| SimulationEngine | MainEngine$1.compare(Event, Event) | 31,611 | 24 (0.0%) | 24 (0.0%) |
| SimulationEngine | MainEngine.getResourceValue(String) | 8,064 | 78 (0.0%) | 23 (0.0%) |
| SimulationEngine | MainEngine.<init>(SimulationVisualization) | 1 | 14 (0.0%) | 14 (0.0%) |
| SimulationEngine | MainEngine.initializeModules() | 1 | 14 (0.0%) | 14 (0.0%) |
| SimulationEngine | MainEngine.generateTriggerEvent(double) | 1,790 | 179 (0.0%) | 7 (0.0%) |
| SimulationEngine | MainEngine.initializeEngine() | 1 | 71 (0.0%) | 7 (0.0%) |
| SimulationEngine | MainEngine.initializeEventQueue() | 1 | 7 (0.0%) | 7 (0.0%) |
| SimulationEngine | MainEngine.generatePlots() | 1 | 11,566 (2.4%) | 3 (0.0%) |
| SimulationEngine | Event.<init>() | 1,790 | 3 (0.0%) | 2 (0.0%) |
| SimulationEngine | MainEngine.run() | 1 | 290,666 (61.1%) | 0 (0.0%) |
| SimulationEngine | Event.getScheduledTime() | 65,012 | 0 (0.0%) | 0 (0.0%) |
Table 4: Call graph usage statistics of iSimBioSys under the 60mins experimental setup: The highlighted regions show the key resource consuming methods of the simulation. The startSimulation() method is invoked at the start of the simulation and takes 61% of the CPU time, the main function within it being the invocation of the run() method of its thread. Another method which is invoked the highest number of times is the getScheduledTime() on an event object, since it reflects the call of the event scheduler. As the queue is implemented using the templatized priority queue of JDK 1.5, the holding time on the method is almost negligible.
It is pertinent to mention here that the population of the initial event list, together with the fact the event list can be scheduled in “batches” rather than on individual events provides immense flexibility to the system in terms of:
• The biological system can be configured to start simulation at different time-points and states by appropriating scheduling “event batches” which update the system resources correspondingly
• Event batch scheduling can be used to sufficiently speed up the simulation [54], particularly in cases where difference in time-scales of event execution times can cause “stiffness” in simulation [23]. This technique is similar in concept to the tauleaping and binomial leap techniques [23] which have been applied in stochastic simulation models based on Gillespie algorithm [19,20] and its variants [22].
As a concluding remark for this section, it may be mentioned that the performance metrics are all for the computer system configuration mentioned in the earlier section and with the JVM executing the simulation process only, while no other user space process is running on the computer system. The graphs also report the average memory and processing usage over 100 runs of simulation for each in silico experiment.
Novelty of the simulation platform
Based on the discussions in the previous sections, we can outline the novelty of the proposed simulation approach in comparison to existing stochastic simulation schemes in the following:
• In existing platforms, the details of the biological functions have to be captured through biochemical reactions having exponential event completion times and the rate constants need to be determined experimentally; our stochastic models [45-48,50,56-66] allows separate biological events to be modeled parametrically to (a) accurately predict the rate constants and the event holding time distributions and (b) determine the probabilities of occurrence of each event type at discrete time instants.
• Current techniques face computational challenges at a “system level” when the number of biochemical reactions in the system becomes extremely large; our platform allows building a flexible multi-scale framework to alleviate this challenge.
• The SSA often suffers from simulation stiffness; our platform provides one the capability of redefining an event, e.g., a set of faster biochemical reactions (see our earlier works [58,60,61]) so as to approximately alleviate stiffness.
Conclusion and future work
In this paper, we have outlined a discrete event based stochastic modeling and simulation framework for studying the complex dynamics of biological processes. The central theme of this approach is based on developing probability distributions of the holding times of the different biological events associated with a process and simulating the temporal dynamics of the molecular events using the discrete event simulator. Currently, our technique is focused on celllevel signal transduction and gene regulatory pathway dynamics. The performance of the simulation framework indicates its suitability on different hardware and software platforms. Although, the current system works on uniform scales of time (~1000millisecs), discrete event based stochastic simulation techniques have been used extensively in networking studies to study systems dynamics at multiple spatio-temporal scales. We are currently working on a hybrid simulation framework which captures the ensemble dynamics of gene regulatory networks (operating in ~1000millisecs time-scale) together with metabolic networks (operating in ~1millisecs time-scale). The flexibility of the modeling technique in abstracting the system at different levels of granularity based on existing knowledge, coupled with the computational power of the simulation framework allows a stochastic event based simulation system to provide an effective in silico framework, in conjunction with accurate and detailed modeling of system parameters, for developing hypothesis tests prior to actual wet-lab experiments.
References
- McCulloch AD, Huber G (2002) “Integrative biological modeling in silico”, ‘In Silico’ Simulation of Biological Processes, Novartis Foundation Symposium 247.
- Pubmed Central, http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?db=PubMed.
- Kitano H (2002) Computational Systems Biology. Nature 420: 206-210.
- Noble D (2004) Modeling the Heart. proceedings of Physiology 19: 191-197.
- Mendes P (1993) GEPASI: A software package for modeling the dynamics, steady states and control of biochemical and other systems. Comput Applic Biosci 9: 563-571.
- Sauro HM (2000) Jarnac: a system for interactive metabolic analysis. Animating the Cellular Map. 9th International BioThermoKinetics Meeting (eds: Hofmeyr JHS, Rohwer JM, Snoep JL) Stellenbosch University Press Ch 33: 221-228.
- Tomita M, Hashimoto K, Takahashi K, Shimizu TS, Matsuzaki Y, et. al (1999) ECell: Software environment for whole cell simulation. Bioinformatics 15: 72- 84.
- Cellier F (1991) Continuous System Modeling. Springer Verlag.
- Ramsey S, Orell D, Bolouri H (2005) Dizzy: Stochastic simulation of large scale genetic regulatory networks. Journal of Bioinformatics and Computational Biology.
- Novre NL, Shimizu TS (2000) StochSim: modeling of stochastic biomolecular processes. Bioinformatics 17: 575-576.
- Ridgway D, Broderick G, Ellison MJ (2006) Accommodating space, time and randomness in network simulation. Curr Opin Biotechnol 17: 493-498.
- Xia XQ, Wise MH (2003) DimSim: A Discrete Event Simulator of Metabolic Networks. Journal of Chemical Information and Computer Sciences 43.
- Kam N, Katz NA, Korman A, Peleg D (2001) The Immune System as a Reactive System: Modeling TCell Activation with StateCharts. Technical Report MCS0109, Mathematics & Computer Science, Weizmann Institute of Science.
- Efroni S, Harel D, Cohen I (2003) Towards rigorous comprehension of biological complexity: Modeling, execution and visualization of thymic t cell maturation. Genome Research 13: 2485–2497.
- de Jong H (2000 ) Modeling and Simulation of genetic regulatory systems: A literature review. Research Report, RR4032, INRIA Rhnealpes, Montbonnot SaintMartin, General.
- Samoilov MS, Arkin AP (2006) Deviant effects in molecular reaction pathways. Nature Biotechnology 24: 1235 - 1240.
- Ginkel M, Kremling A, Nutsch T, Rehner R, Gilles ED (2003) Modular modeling of cellular systems with ProMoT/Diva. Bioinformatics 19: 1169-1176.
- Van Gend C, Kummer U (2001) STODE automatic stochastic simulation of systems described by differential equations. International Conference of Systems Biology.
- Gillespie DT (1976) A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J Comput Phys 22: 403-434.
- Gillespie DT (1977) Concerning the validity of the stochastic approach of chemical kinetics. J Stat Phys 16: 311-319.
- Gibson MA, Bruck J (2000) Efficient Exact Stochastic Simulation of Chemical Systems with Many Species and Many Channels. Journal of Physical Chemistry A 104: 1876–1889.
- Gillespie DT (2001) Approximate accelerated stochastic simulation of chemically reacting systems. J Chem Phys 115: 1716–1733.
- Tian T, Burrage K (2004) Binomial leap methods for simulating stochastic chemical kinetics. J Chem Phys 121: 10356–10364.
- Chatterjee A, Mayawala K, Edwards JS, Vlachos DG (2005) Time accelerated Monte Carlo simulations of biological networks using the binomial tau-leap method. Bioinformatics 21: 2136-2137.
- Virtual Cell Project, http://www.nrcam.uchc.edu/.
- Haas P (2002) Stochastic petri nets: Modelling, stability, simulation. Springer ISBN: 978-0-387-95445-5.
- Goss PJ, Peccoud J (1998) Quantitative modeling of stochastic systems in molecular biology by using stochastic Petri nets. Proc Natl Acad Sci USA. 95: 6750-6755.
- Matsuno H, Doi A, Nagasaki M, Miyano S (2000) Hybrid Petri net representation of gene regulatory networks. Pacific Symposium on Biocomputing 5 341352.
- Calder M, Gilmore S, Hillston J (2006) Modelling the influence of RKIP on the ERK signalling pathway using the stochastic process algebra PEPA. Transactions on Computational Systems Biology 4230: 1-23. ISSN 0302-9743.
- Kuttler C (2005) Bacterial transcription in the pi calculus. In Proceedings of Computational Methods in Systems Biology (CMSB), ed. G. Plotkin.
- Regev A (2001) Representation and simulation of molecular pathways in the stochastic pi-calculus. In Proceedings of the 2nd workshop on Computation of Biochemical Pathways and Genetic Networks.
- Zeigler B, Praehofer H, Kim T (2000) Theory of Modeling and Simulation. London: Academic Press.
- Uhrmacher AM, Priami C (2005) Discrete event systems specification in systems biology - a discussion of stochastic pi calculus and DEVS. Proceedings of the Winter Simulation Conference.
- Calder M, Gilmore S, Hillston J (2005) Automatically deriving ODEs from process algebra models of signalling pathways. In the proceedings of the Computational Methods in Systems Biology workshop (CMSB).
- Uhrmacher AM (1997) Concepts of Object and Agent Oriented Simulation. Transactions of the Society for Computer Simulation International 14: 59-67.
- Uhrmacher AM, Tyschler P, Tyschler D (2000) Modeling and Simulation of Mobile Agents. Future Generation Computer Systems 17: 107-118.
- Himmelspach J, Uhrmacher A (2004) A component based simulation layer for JAMES. In Proc. of the 18th Workshop on Parallel and Distributed Simulation (PADS) 115–122.
- Emonet T, Macal CM, North MJ, Wickersham CE, Cluzel P (2005) AgentCell: A Digital Single-Cell Assay for Bacterial Chemotaxis. Bioinformatics 21: 2714- 2721.
- Park S, Hunt CA, Glen EP, Ropella C (2005) PISL: A Large-Scale In Silico Experimental Framework for Agent-Directed Physiological Models. Spring Simulation Multiconference The Society for Modeling and Simulation International.
- Sheikh-Bahaei S, Glen EP, Ropella C, Hunt A (2005) Agent-Based Simulation of In Vitro Hepatic Drug Metabolism: In Silico Hepatic Intrinsic Clearance. Spring Simulation Multiconference The Society for Modeling and Simulation.
- Zhang T, Rohlfs R, Schwartz R (2005) Implementation of a discrete event simulator for biological self-assembly systems. Proc Winter Simulation Conf 2223-2231.
- Zeigler BP (2000) Theory of Modeling and Simulation. Academic Press.
- Zeng X, Bagrodia R, Gerla M (1998) GloMoSim: A Library for Parallel Simulation of Large-Scale Wireless Networks. pads, p. 154, 12th Workshop on Parallel and Distributed Simulation (PADS’98), 1998.
- Rangavajhala VK, Daefler S (2003) Modeling the Salmonella PHOPQ Two Component Regulatory System. Master’s Thesis UTA.
- Ghosh P, Ghosh S, Basu K, Das S (2005) A Diffusion Model to Estimate the Inter-arrival Time of Charged Molecules in Stochastic Event based Modeling of Complex Biological Networks. IEEE Computational Systems Bioinformatics Conference (CSB) 19-21.
- Ghosh P, Basu K, Das S, Zhang C (2010) Discrete diffusion models to study the effects of Mg2+ concentration on the PhoPQ signal transduction system. In press BMC Genomics 2010 11: S3.
- Ghosh P, Ghosh S, Basu K, Das S (2008) Holding Time Estimation for Reactions in Stochastic Event-based Simulation of Complex Biological Systems, Elsevier Simulation Modeling Practice and Theory 16: 1615-1639.
- Ghosh P, Ghosh S, Basu K, Das S(2009) In-silico effects of Mg2+ concentration on the PhoPQ signal transduction system. International Joint Conferences on Bionformatics, Systems Biology and Intelligent Computing (IJCBS) 405-411.
- Degenring D, Rhl M, Uhrmacher AM (2003) Discrete Event Simulation for a Better Understanding of Metabolite Channeling. In Proc Of the International Workshop on Computational Methods in Systems Biology, 2426.
- Ghosh P, Ghosh S, Basu K, Das SK, Daefler S (2006) Stochastic Modeling of Cytoplasmic Reactions in Complex Biological Systems. 6th IEE International Conference on Computational Science and its Applications (ICCSA) 566-576.
- Keseler IM, Collado-Vides J, Gama-Castro S, Ingraham J, Paley S(2005) EcoCyc: a comprehensive database resource for Escherichia coli. Nucleic Acids Res 33: D334-D337.
- Java 1.5 Platform, www.java.sun.com.
- CCDB Database, http://redpoll.pharmacy.ualberta.ca/CCDB/
- Lok L (2004) The need for speed in stochastic simulation. Nat Biotechnol 22: 964–965.
- Detweiler CS, Cunanan DB, Falkow S (2001) Host microarray analysis reveals a role for the Salmonella response regulator phoP in human macrophage cell death. Proc Natl Acad Sci 98: 5850-5855.
- Ghosh P, Ghosh S, Basu K, Das S (2006) An Analytical Model to Estimate the time taken for Cytoplasmic Reactions for Stochastic Simulation of Complex Biological Systems. IEEE Granular Computing Conference 2006 79-84.
- Mayo M, Perkins E, Ghosh P (2011) Downstream Exploration of DNA-Bound Searching Proteins: a Diffusion-Reaction Model. IEEE BIBE 2011.
- Ghosh P, Ghosh S, Basu K, Das S (2007) A Markov Model based Analysis of Stochastic Biochemical Systems. LSS Computational Systems Bioinformatics Conference (CSB) 121-132.
- Ghosh P, Ghosh S, Basu K, Das S, Daeffler, S (2007) Modeling protein-DNA binding time in Stochastic Discrete Event Simulation of Biological Processes. IEEE Symposium on Computational Intelligence in Bioinformatics and Computational Biology 439-446.
- Ghosh S, Ghosh P, Basu K, Das S (2007) Modeling the stochastic dynamics of gene expression in single cells: A Birth and Death Markov Chain Analysis. IEEE International Conference on Bioinformatics and Biomedicine 308-316.
- Ghosh S, Ghosh P, Basu K, Das S Modeling the stochastic dynamics of protein synthesis: A discrete event simulation approach. Biotechnology and Bioinformatics Symposium (BIOT-2007), Colorado Springs, 2007, pp. 1-6.
- Ghosh P, Ghosh S, Basu K, Das S, Daeffler S (2006) A stochastic model to estimate the time taken for protein-ligand docking. IEEE Symposium on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB) 1-8.
- Ghosh P, Ghosh S, Basu K, Das S, Daeffler S (2007) A Computationally Fast and Parametric Model to estimate Protein-Ligand Docking time for Stochastic Event based Simulation. LNCS Transactions on Computational Systems Biology 4780: 14-41.
- Ghosh P, Ghosh S, Basu K, Das S (2009) Parametric modeling of protein- DNA binding kinetics: A Discrete Event based Simulation approach. Journal of Discrete Applied Mathematics 157: 2395-2415.
- Ghosh P, Dullea R, Fischer J, Turi T, Sarver R, et. al (2009) Comparing 2-nt 3’ overhangs against blunt ended siRNAs: A systems biology based study. BMC Genomics 10: S17 1-14.
- Mayo M, Perkins E, Ghosh P (2011) First-Passage Time Analysis of a One- Dimensional Diffusion-Reaction Model: Application to Protein Transport along DNA. In press, BMC Bioinformatics 2011.
Relevant Topics
- Agricultural biotechnology
- Animal biotechnology
- Applied Biotechnology
- Biocatalysis
- Biofabrication
- Biomaterial implants
- Biomaterial-Based Drug Delivery Systems
- Bioprinting of Tissue Constructs
- Biotechnology applications
- Cardiovascular biomaterials
- CRISPR-Cas9 in Biotechnology
- Nano biotechnology
- Smart Biomaterials
- White/industrial biotechnology
Recommended Journals
Article Tools
Article Usage
- Total views: 17584
- [From(publication date):
specialissue-2014 - Aug 16, 2025] - Breakdown by view type
- HTML page views : 12853
- PDF downloads : 4731