Research Article Open Access
A Study of Impacts of Temperature Components on Precipitation in Iran Using SEM-PLS-GIS
| Javari M* | |
| College of Social Science, PayameNoor University, Iran | |
| Corresponding Author : | Javari M Assistant Prof. of Climatology College of Social Science PayameNoor University, Iran Tel: +98 (21) 2244 2042 E-mail: majid_javari@yahoo.com |
| Received April 25, 2015; Accepted May 18, 2015; Published May 28, 2015 | |
| Citation: Javari M (2015) A Study of Impacts of Temperature Components on Precipitation in Iran Using SEM-PLS-GIS. J Earth Sci Climat Change S3:004. doi: 10.4172/2157-7617.S3-004 | |
| Copyright: © 2015 Javari M. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited. | |
Visit for more related articles at Journal of Earth Science & Climatic Change
Abstract
Structural equation modeling (SEM) is a quantitative technique for evaluating the causal relations between and among a number of variables using a combination of statistical methods and assumptions. Although there have been recent developments in expanding SEM to include climatic changes, most applications have been restricted to the simulation of causal processes; this is especially true for the modelling of environmental changes. However, when SEM is applied as an exploratory technique in climate studies, the proposed model can illustrate and examine the relationships among several climatic elements in the environment. To investigate the relationship between temperature and precipitation, a combination of SEM, partial least squares (PLS) and GIS methods were employed in this study. A measurement model, a structural model and a spatial model for examining the relationships between temperature and precipitation were proposed. A SEM-PLS-GIS model consisting of three measurement sub-models was created on the basis of the concentration values of 14 climatic elements; the data were the monthly and seasonal values for the period between 1975 and 2012, and were obtained from 140 stations. The results of the new SEM-PLS-GIS model showed that seven temperature factors affected, directly or indirectly, the precipitation with minimum temperatures were being the most effective of all. It can be concluded that employing SEM-PLS-GIS model for the purpose of describing causal patterns of climate variations especially the variations of precipitation can be of great value.
| Keywords |
| Causal modeling; SEM-PLS-GIS model; Temperature effects; Precipitation spatial variations |
| Introduction |
| Within the context of zonal changes, extreme precipitation events have recently received much attention because they are more sensitive to precipitation changes than mean values [1]. Particularly, many researchers have placed special emphasis on precipitation variations and their impact on the environment [2]. The importance of temperature variations and anomalies for temporal variations in the precipitation has been well recognized [3]. Temperature variations and anomalies can enhance rainfall through hydrological process. On the other hand, temperature changes which are associated with other climatic elements can highly intensify the formation of precipitation. Due to the close relationship between temperature variations and precipitation variations, the temperature anomalies in one zone can impact the other zones through climatic changes in precipitation processes [4]. Temperature extremes receive much attention as trends in extreme events react more sensitively to climate change than mean climate, and therefore have a more intense impact on precipitation and precipitation formation [5]. Subtropical temperature patterns are the key mechanisms of precipitation in the subtropics and have been reported to play a significant role in mid-latitude extreme precipitation events [6,7]. Causal explanation and climatic prediction are distinct challenges facing climatic modelling. Structural modelling draws on hypotheses from a priori theory to specify causal relationships between temperature and precipitation variables [8]. SEM is used to estimate the interrelationships among temperature and precipitation in the study. Although the focus was on the three core elements of temperature (i.e. maximum temperatures, minimum temperatures and temperature indexes), the influences of temporal and spatial temperature on precipitation intention were also investigated [9,10]. The development of SEM in climate study was regarded as an important statistical development in the recent decades. The SEM simultaneously carries out causal analysis and path analysis; it can (1) measure errors of observed variables, (2) represent ambiguous constructs in the form of unobserved variables by using several manifest variables and (3) estimate causal relationships among both latent and manifest variables [11].That is why SEM examines the precipitation changes model by comparing it with multiple regressions and with regard to the nature to paths, separate elements and distinct coefficients. The SEM method permits checking and examining a complete model by generating goodness-of-fit statistics and assessing the overall fit. SEM also allows for the expansion of statistical estimation by assessing and estimating terms of error and fit indexes for temperature and precipitation variables [12,13]. However, SEM is similar to using multiple regression analysis in precipitation changes analysis [11,14]. The partial least squares structural equation modeling method has recently gained increasing attention not only in studying the climate and climatic changes but also in precipitation variations modeling, temperature effective research, temperature variation patterns and other climatic research [6,15-17]. One of the approaches which examine the link from the construct to the indicators based on reflective measurement is partial least squares structural equation modeling [18]. The other approach examining the link from the indicators to the construct is called formative measurement [19-21]. However, recent advances in explanatory modelling of climatic analysis now enable a consistent, statistical evaluation of expert knowledge as the basis for modeling specifically through the SEM framework [22]. The regional responses of precipitation extremes to climate changes are diverse. In this study, the joint temperature behaviors of thirteen elements of temperature indices in precipitation variations in Iran are studied. We also investigated the direct and indirect effects of temperature elements change on precipitation. Unlike most previous research where each indicator is evaluated separately, this study analyzes three latent variables as representing overall precipitation. The same approach is employed to define the conditions of precipitation changes and internal operation constructs. The results could be used by environmental management to study the following two questions: a) Does the precipitation situation of a country affect the climatic condition and environment management? b) Does the precipitation condition affect the overall internal operation and will it eventually affect the overall precipitation of Iran? While the answer is quite obvious, this analysis takes a different approach by examining the effect of a combination of temperature indicators regarding overall precipitation and, hence, giving environmental managers a clearer picture of the situation as they make decisions. To answer these questions, we need a unified model to investigate the relationships between and among temperature and precipitation variables. SEM can be employed as a versatile statistical technique to provide a suitable framework for the causal analysis of precipitation patterns and precipitation variations. The rest of the paper is organized as follows: in Section 2, we briefly introduced the SEM and the PLS methods to provide a description of our proposed temperature effects on framework of precipitation. Section 3 presents the new modeling of precipitation variations in detail. The experimental results and conclusions are presented in Sections 4 and 5 respectively. |
| Background |
| This paper employs the SEM-PLS-GIS methods for investigating the variations in precipitation patterns. The next subsections provide a brief introduction to these three algorithms to make this paper more reader-friendly and self-contained. |
| SEM as a means to study precipitation variations |
| ¨ |
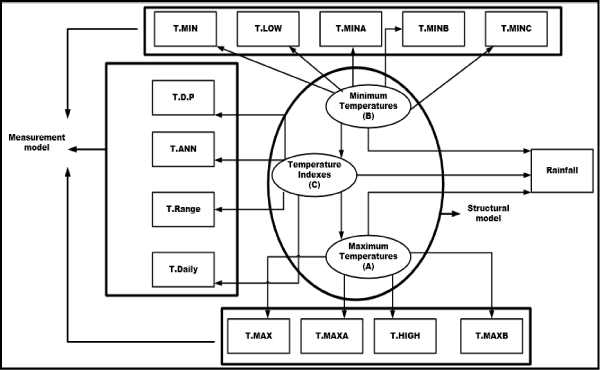
| The SEM has been regarded as an inclusive and valuable statistical method in climatology in recent years. This multivariate analysis method has been widely applied for theoretical explorations and empirical analysis in environmental disciplines [23,24]. It describes and tests the relationships between latent and manifest variables [25]. As presented in Figure 1, a structural equation model usually consists of two main components, a structural model and several measurement models. The measurement model includes a latent variable, a few associated observed variables and their corresponding measurement errors. The structural model, however, consists of all latent variables and their interrelationships [26]. Figure 1 provides a simple representation of a structural equation model investigating the effect of latent variables (Maximum Temperatures, Minimum Temperatures and Temperature Indexes) and the manifest variables which are used to represent the latent variables. The manifest variables are shown in rectangles, the latent variables in ellipses, measurement errors in circles with arrows indicating the direction of the effects Figure 1 shows the manifest variables modeled based on a reflective measurement model. To establish a common terminology for the discussion that follows, we will briefly review some special issues. Using the AMOS (It is available from the http://www-03.ibm.com/software/products/en/spss-amos), SmartPLS (It is available from the http://CRAN.R-project.org/package=semPLS) and ArcGIS software (It is available from the http://www.esri. com/software/arcgis), a structural equation model can be stated as follow [25,27-29]: |
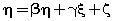 (1) (1) |
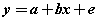 (2) (2) |
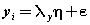 (3) (3) |
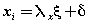 (4) (4) |
| where x represents the independent variable,E represents error,η represents internal latent variable, ξ represents external latent variable, β represents internal variables coefficients, γ represents external variables coefficients, ζ represents error of internal variables, δ represents error of external indicators, λx represents coefficient of external variables for external indicators,λy represents coefficient of internal variables for internal indicators and e represents error to internal indicators. The values are equations coefficients. Equation (1) is called the latent variable or structural model and expresses the hypothesized relationships among the constructs. Equations (2), (3) and (4) are factor-analytic measurement models which tie the constructs to observable indicators [30]. However, structural equation models comprise both a measurement model and a structural model. The measurement model relates observed responses or ‘indicators’ to latent variables and sometimes to observed covariates. The structural model then specifies relations among latent variables and regressions of latent variables on observed variables [31]. In SEM, three types of effects, that is, direct, indirect and total effects are estimated. Direct effects, shown by single-directional straight arrows, represent the relationship between one latent variable to another. It should be noted that the arrows used in SEM indicate directionality and not causality. Indirect effects, on the other hand, reflect the relationship between an independent latent variable (exogenous variable) and a dependent latent variable (endogenous variable) that is mediated by one or more latent variables. The total effect is the sum of direct and indirect effects [32]. Algorithm 1 represents an SEM algorithm which consists of six stages and various parameters of goodness fit: AFI, CFI, PFI,X2,GFI,ACFI,RMR,TLI,NFI, NC,IFI. PRATIO, PNFI and …. and control how much fitting of analysis model is imposed in each iteration. The SEM algorithm includes the following six steps in Algorithm 1: |
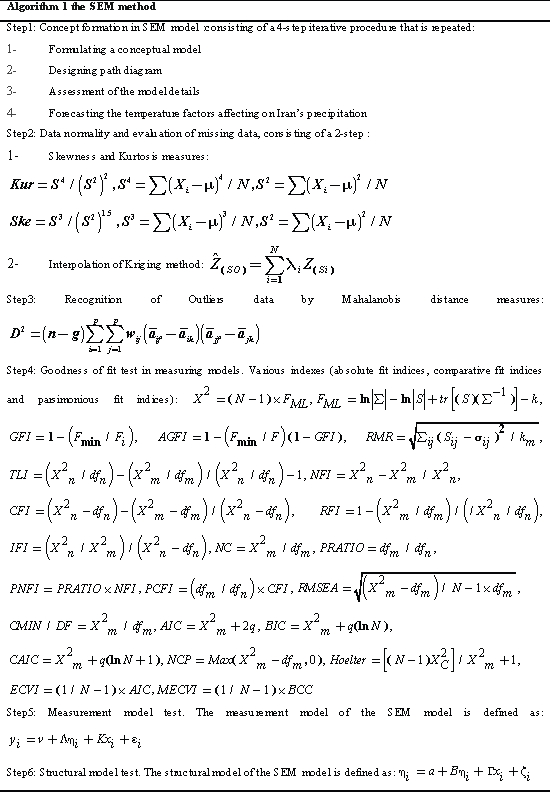 |
| Partial least squares (PLS) method |
| The concept of partial least squares was introduced by S. Wold, Kettaneh-Wold, and Skagerberg [33]. PLS a multivariate linear regression method, has established itself as an important analytical tool in climatic analysis [34]. A PLS path model consists of two elements. First, there is a structural model that represents the constructs (circles or ovals). The structural model also displays the relationships (paths) between the constructs. Second, there are the measurement models of the constructs and the weighting scheme that display the relationships between the constructs and the indicator variables (rectangles) [35,36]. In PLS, the measurement model specifies how the latent variables (constructs) are measured [27]. Generally, there are two different ways to measure unobservable variables. One approach is referred to as reflective measurement, and the other is called formative measurement. Structural model shows how the latent variables are related to each other (i.e., it shows the constructs and the path relationships between them). The location and sequence of the constructs are based on a model or the researcher’s experience and accumulated knowledge [37,38]. Reflective measurement can be stated in the following form [39]: |
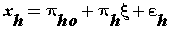 (5) (5) |
| Equation (5) is called the reflective method in PLS where ξ is the latent variable and εis the error. Structural model can be formulated in the following form [39,40]: |
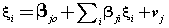 (6) (6) |
| However, there are two approaches to estimate the relationships in a structural equation model. The more widely applied one is the SEM approach and the other is PLS-SEM which is the focus of this paper. Algorithm 2 displays the full explanation of the PLS method. The PLS path modeling method was developed by Wold and the PLS algorithm is essentially a sequence of regressions in terms of weight vectors [41]. The weight vectors obtained at convergence satisfy fixed point equations [27]. The basic PLS algorithm, as suggested by Joseph [39,40], includes the following three steps in Algorithm 2. |
 |
| New SEM-PLS-GIS method |
| In this study, a new SEM method is proposed based on PLS-SEM-GIS, which combines the principles of SEM measurement model and PLS, SEM structural model and PLS, and trend spatial analysis by GIS. Thus, the new mathematical model can not only generate factors to form a structural model but also ensure the optimum relationship to the objective dependent variables .This method consists of ten steps: 1) the concept formation in SEM model, 2) examining the data normality and evaluation of the missing data, 3) examining the outliers in the data to more precisely forecast the precipitation changes 4) selection and initialization of the goodness of fit test in measuring models, 5) studying the reliability of measurement model, 6) studying the reliability of structural model, 7) determining the distribution of data in the SEM-PLS measurement and structural models by GIS, 8) measuring the standard distance (spatial statistics), 9) examining the geographical weighted regression and 10) drawing the maps of direct, indirect and total effects. The maps of the effects of the selected climatic elements in Iran were provided with a higher accuracy using this method. Finally, the trend maps of temperatures effects on precipitation were drawn. Trend spatial analysis of the effects allows us to model, examine, and explore spatial relationships and helps explain the factors behind observed spatial patterns [42]. By modeling spatial relationships, however, spatial trend analysis and prediction of the temperature effects on precipitation have also been done. Modeling the factors that contribute to precipitation, enables us to make predictions about precipitation and climatic changes [42,43]. In this paper the new mathematical model of SEM-PLS-GIS is introduced and its applicability in climatic data processing is validated by a case study for identifying the factors associated with precipitation change patterns in Iran. The case study uses concentration values of 14 elements obtained from 140 station samples in the study area. For comparison purposes, all three methods, i.e. SEM, PLS and GIS were used for analyzing the dataset. To implement the GIS and the new SEM –PLS-GIS method, precipitation was taken as the dependent variable and the other elements as the independent variables. In order to interpret the climatic associations of latent variables from the precipitation point of view, the loadings and regression coefficients of latent variables are important [44,45]. Algorithm 3 explains the SEM-PLS-GIS method; the steps of the proposed algorithm are as follows. |
 |
| Materials and Methods |
| Materials |
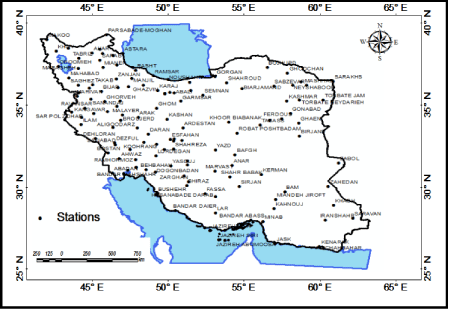
| Iran, situated in the southwest of Asia, ranges from 25°3’ to 39°47’ N and from 44°5’ to 63°18’ E. The case study dealt with the identification of temperatures effect on precipitation in order to better forecast the precipitation variations in Iran. Precipitation variations can be defined from various aspects, such as effectiveness of precipitation formation factors or even climatic events such as drought. With regard to precipitation changes in Iran, we chose thirteen temperature indices, namely: 1. Annual average temperature (T.AAN) 2. Average minimum temperature (T.MIN) 3. Average maximum temperature (T.MAX) 4. Dew point temperature (T.D.P) 5. Temperature range (T. Range) 6. Daily temperature (T.Daily) 7. Recorded absolute maximum (T. MAXA) and minimum temperature (T. MINA) 8. Number of days with maximum temperature equal and lower than 0°C (T.MAXB) 9. Number of days with maximum temperature equal and higher than 30°C (T.HIGH) 10. Number of days with minimum temperature 11. Number of days with minimum temperature equal and lower than -4°C 12) number of days with minimum temperature equal and lower than 0°C (T. MINC) 13. Number of days with minimum temperature equal and higher than 21°C (T. LOW). The chosen indices were obtained from meteorological organization and included the monthly, seasonal and annual information of 140 stations in Iran for the period of 1975-2012 (Figure 2). All the observed precipitation data have been subject to strict quality control obtained from http://www.irimo.ir/eng/wd/720- Products-Services.html. The study focused on monthly and seasonal variations. For this purpose, a harmonic analysis was applied to all data, and data were studied with respect to the time defaults, linearity, normality, missing data, outliers etc. at different phases of the research. |
| Methods |
| Prediction of temperatures effect on precipitation changes are based on exploratory and confirmatory analyses with the incorporation of direct, indirect and total effects of predictor variables on response variables. SEM-PLS-GIS is a multivariate statistical technique that uses factor analysis, PLS analysis, path analysis and spatial analysis to evaluate the relationship between temperatures and precipitation [28,46]. Application of this technique in climatology leads to this question of how the causal relationships among latent variables and the climatic factors are studied. Path analysis can be used to answer this question. In organizing this paper, the following phases were considered: |
| Concept formation model: To test the absolute effects of temperature elements on precipitation, we performed a confirmatory and exploratory path analysis, which identifies the most likely causal links among correlated variables [47]. We studied the possible causal paths between temperature and precipitation. Direct, indirect and the total effects of temperatures on precipitation is highly related to the causal link between temperatures and precipitation. Nevertheless, temperature could influence precipitation, which in turn affects amount, with only no direct link between temperatures and precipitation. Moreover, paths differences could also directly influence temperatures and precipitation. We studied ten possible cause–effect |
| linkage models for each measure of temperatures at each stage (Figure 3). For causal analysis of temperature factors, different symbols were used in order to show the relationships among temperatures elements and precipitation. Formulating a conceptual model, designing path diagram, assessment of the model details and forecasting the temperature factors affecting Iran’s precipitation were done. In formulating the conceptual model, the relationships between the temperatures and precipitation have been taken into account. We also explored the relationships between each measure of temperature and precipitation because primary analyses showed different relationships within temperature factors. When analyzing, the effect of factors on precipitation and the rate of this impact were studied. Standard series of covariance values among exogenous variables and correlation coefficients among the series were also examined to determine the relationships among the conceptual model paths of the research [48]. Through estimating the standard of the series, the regression weights of the series were identified. Through estimating simple moments in addition to variance-covariance evaluation, the typical covariance of the series and typical correlation matrix of the series were estimated. By estimating implied moments or all implied moments, covariance was identified based on the temperature factors and the reconstructed correlation matrix was based on the temperature factors; the variance-covariance reconstruction was also identified. Moreover, direct, indirect and total effects of the series were determined as standardized and non-standardized values and squared multiple correlation coefficients between each endogenous variable and other variables of the model were calculated. To assess the relative importance of direct, indirect and total effects of temperature on precipitation, we compared standardized and non-standardized coefficients. By estimating factor score weights, the capability of each variable in predicting the studied series was revealed. Through estimating threshold ratio or critical ratio for the difference between the factors, other factors are carefully compared. As for the temperature variables, we used the calculated minimum temperature, which was found to be the best predictor of precipitation among temperature factors. |
| Data normality assumption and evaluation of missing data: We examined graphically and statistically the relationship between the temperature and precipitation variables; temperature and precipitation variables were normally fitted. We did not use data from one single station because the number of data points varied widely in Iran. In this paper, some of the stations were omitted due to the lack of sufficient data. Reconstruction of variables was done using least squares and kriging methods. Kriging models are very valuably in identifying ambiguous points and their fittings. These two methods may be calculated using the following relations: |
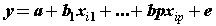 (7) (7) |
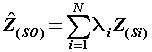 (8) (8) |
| Where: P is the prediction period, Z (si) the value of the data measurement at its position, λi weight for measuring value, so the prediction value at that position and N the number of measured values. We used least square and kriging to explore whether there were significant relationships between temperature factors and precipitation. |
| Recognition of outliers in the data: Outliers are scores that are different from the rest. One of the factors influencing the data normality is the presence of the data whose values are substantially different from the other data and their distance is high to the extremes. Deleting these data is effective for providing better results on research plan. To detect single-variable port data, it is enough to standardize the total data. Accordingly, the data must demonstrate the following characteristics: there should be no outliers in the data [12]. To detect multi-variable port data, Mahalanobis Distinct Index was used: |
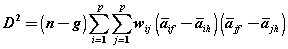 (9) (9) |
| Where, aif is the mean for ith variable in group, f wij is an element from the inverse of the pooled within groups covariance matrix (down weights correlated variables), n is the number of sample units, g is the number of groups, and i ≠ j. This index is a typical average for the whole variables and its higher values indicate that the variables are placed at a further distance from the general distribution of the sample and vice-versa. To measure latent and observed variables, the variables were studied individually. In the first phase, regressive weights of the series were studied. Also, to make the series scales homogenous, standard regressive weights of the series were studied and the effect sizes of the variables were also calculated. Moreover, to study the significance level of the model, the variables were studied using their significance level considering the critical ratio of variables. |
| Goodness of fit test in measuring models |
| Goodness of fit index was used in this study. Hence, absolute fit indices (AFI), comparative fit indices (CFI) and parsimonious fit indices (PFI) were considered. Comparative fit index is based on comparing the model with competitor models and parsimonious fit index is dependent on the desired parameters of the researcher. Absolute fit indices include chi-square index (X2), goodness of fit index (GFI), adjusted goodness of fit index (AGFI) and root mean squared residual (RMR), (Fernando Gutiérrez, 2014). Comparative or relative fit index includes Tucker-Lewis index (TLI), Bentler-Bonnet index (NFI), comparative fit index (CFI), relative fit index (RFI), and incremental fit index (IFI). Parsimonious fit indices include; normed chi-square (NC), parsimony ratio (PRATIO), parsimonious normed fit index (PNFI), parsimonious goodness fit index (PGFI), root average squared error of approximation (RMSEA) and normed chi-square (CMIN/DF). To compare the models, Akaike information criterion indices (AIC), Browne-Cudeck criterion (BCC), Bayes information criterion (BIS), consistent version of Akaike information criterion (CAIC), non-central parameter (NCP), Hoelter non-central parameter (NCP), Hoelter’s index, (HOELTER), expected cross-validation index (ECVI) and modified expected cross-validation index (MECVI) are used (Table 1). |
| Measurement model |
| The measurement model of SEM allows the researcher to evaluate how well his or her observed (measured) variables were combined to identify underlying hypothesized constructs. Confirmatory factor analysis is used in testing the measurement model, and the hypothesized factors are referred to as latent variables. A measurement model in SEM defines the association between the variables of interest. It provides the link between scores on a measuring instrument and the underlying constructs they are designed to measure. The measurement model is tested to validate the measurement instruments. The basic equations of the structural and measurement models are the following: |
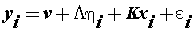 (10) (10) |
| Where η is an m-dimensional vector of latent variables, x is a q-dimensional vector of covariates, ε is a p-dimensional vector of residuals or measurement errors which are uncorrelated with other variables, v is a p-dimensional parameter vector of measurement intercepts, L is a p × m parameter matrix of measurement slopes or factor loadings, and K is a p × q parameter matrix of regression slopes. |
| Structural model |
| Equations in the structural portion of the model specify the hypothesized relationships among latent variables. The structural model is defined in terms of the latent variables regressed on each other and the q-dimensional vector x of independent variables [49-51]: |
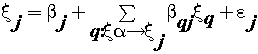 (11) (11) |
| where ξj is the generic endogenous latent variable, β is the generic path coefficient interrelating the q-th exogenous latent variable to the j-th endogenous one, and εj is the error in the inner relation. We include one hypothesized structural model in the composite model in Figure 2. In this model, we hypothesize that conceptual elements provide a function of particular concepts for several issues. We can describe relationships among latent variables as covariance, direct effects, or indirect effects. We showed those pictorially using double-headed arrows. Because we did not anticipate any non-directional relationships between the latent variables, we specified no covariance in the structural model in Figure 3. Direct effects are relationships among measured and latent variables. We showed those pictorially using single-directional arrows. An indirect effect is the relationship between an independent latent variable and a dependent latent variable that is mediated by one or more latent variables. Mediation may be full or partial. Figure 3 shows the assumed relations with regard to the direct, indirect and total effects. |
| Results and Discussion |
| Measurement model test |
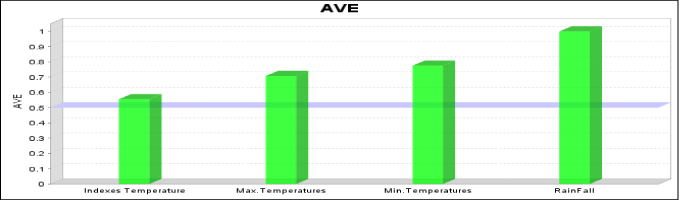
| A pointed out, SEM studies the effect of latent variables or the variables which are not directly observable [52]. These latent variables are measured by several observed variables. Concerning the effects of temperature variables on precipitation, three indicators that is, maximum temperatures, minimum temperatures and temperature indexes were found to influence precipitation (Figure 1). With respect to designing conceptual model, testing the model is done along with testing the measurement model and structural model. Studies on the reliability and validity of measuring tool, on testing the structural models, and on the effects of temperature variables on precipitation in Iran have been conducted [53]. Hence, the PLS method includes two measuring model and structural model tests [54]. Measurement model test includes the study of reliability and validity for identifying the model. To study the reliability, three criteria including the reliability of observed variables, composition validity of the constructs and average variance extracted (AVE) were calculated [55] and the results are shown in Table 2. The results show that the data are significant for the final model (Figure 4). To study the diagnostic validity, two criteria were suggested; first, the indicators of a construct should have higher factor loadings for their construct, that is, the lowest cross-loading to other constructs. Tenenhaus et al. [56] suggest that factor loading of each indicator on the related construct should be at least 0.1 higher than the factor loading of the same indicator on other constructs. Secondly, AVE nth root of a construct should be more than the correlation of that construct with other constructs. In addition, the positive value of this index indicates the suitable quality of measuring tools while negative values show the low quality of tools in measuring the target hidden variable. As shown in Table 2, values higher than 0.7 are the indicators of suitable composite reliability. Hence, the constructs showed a suitable composite reliability. To study the second criterion, it is necessary that nth root series of AVE be taken and substituted by the mentioned matrix diameter instead of correlation matrix of latent variables [56], so that the value of the mentioned matrix diameter should be higher than 0.7. Hence, the results in Figure 5 show that the series have an acceptable condition and the mentioned constructs of research have a suitable diagnostic validity. To study validity, Cross Loading study was used to see if the factor loading on the target construct is 0.1 higher than that on the other construct [57]. As Table 3 shows, the constructs are with an appropriate validity. Finally, to study the quality of measuring instruments (tools), Construct Cross Validated Communality was used [58]. Table 4 shows the sum of squared of the observations for each block (SSO) and for each latent variable block, and the sum of square of prediction errors for block communality (SSE) for each hidden block, as well as the inspection index of communality validity (CV) [59]. Since the coefficient of the mentioned index is positive in Table 4, the measuring model has an appropriate quality. |
| Structural model test |
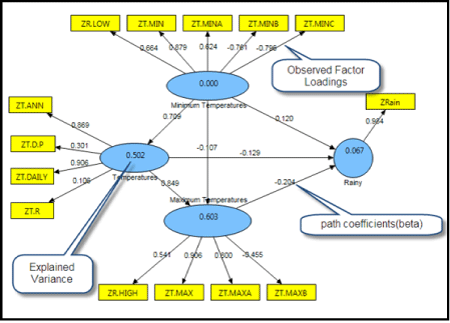
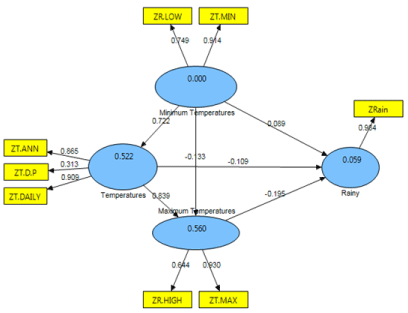
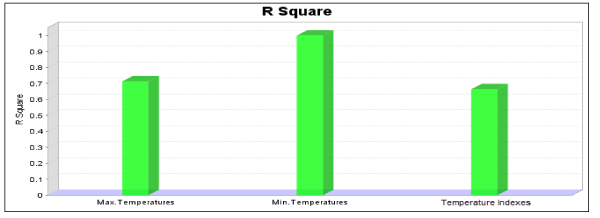
| After studying the measuring model, structural model should be studied and tested. To test the structural model, path coefficients (β), significance of path coefficients and coefficient of determination values should be studied. In addition, to examining the quality of the structural model, Stone-Giser coefficient, Q2, or CV-redundancy study should also be used [60]. t values of 1.96 at significance level of 0.05 were set for studying the path coefficients. Figure 6 shows coefficient of determination values or clarified variance of each latent dependent variable. Hence, the variance for minimum temperature is 0.903, that is, minimum temperature predicts 90 percent of the precipitation changes. To study the significance of the path, t-test (outer model T-statistic) may be used. As Table 5 shows, all paths were higher than 2.66 at 0.01 level of significance. Table 6 shows the significance values of the total effects (total effects, average, STDEV, T-values). Since the t values of variables are higher than 2.66, the total effects of all variables are at 0.01 level with low significance. In addition, to study the quality of structural model, construct cross validated redundancy coefficient may be utilized [18]. As shown in Table 7, the values of the mentioned coefficient or Q2 coefficient are positive, so the structural model enjoys an appropriate quality. |
| Spatial distribution of effects |
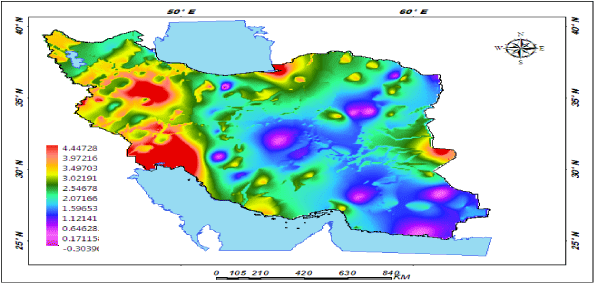
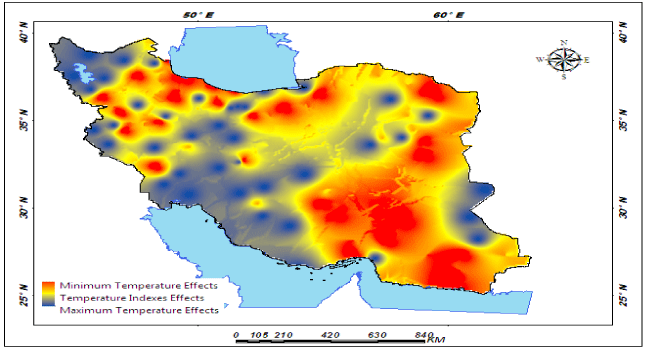
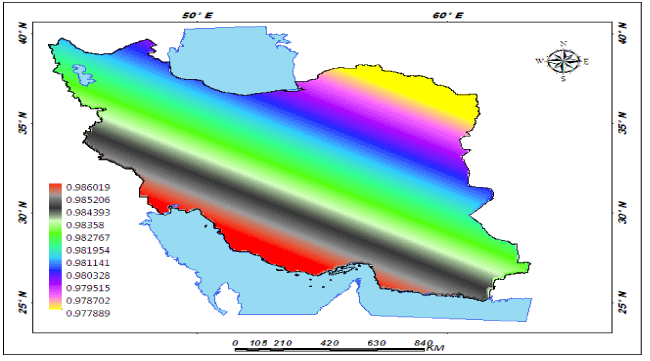
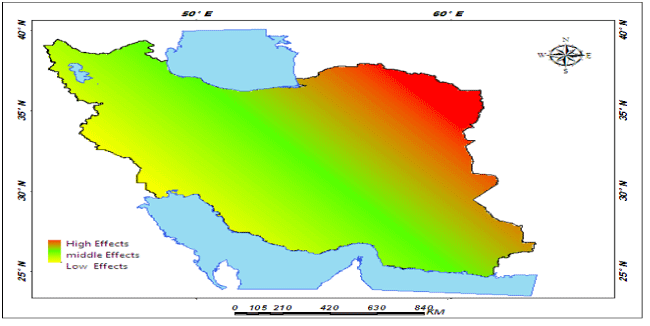
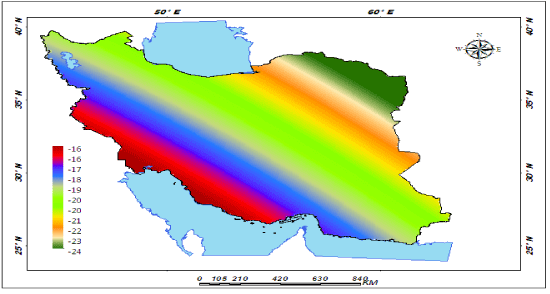
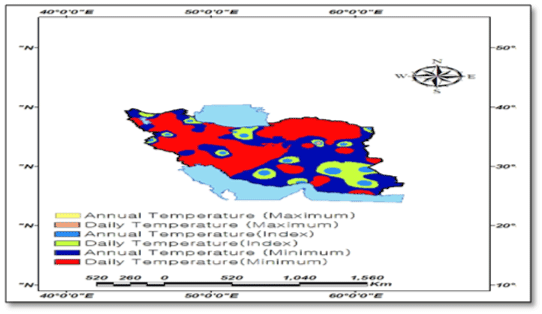
| The findings of this research showed that among the three components, minimum temperature had the largest direct effect on precipitation with an average effect coefficient of 2.67, and maximum temperature had the smallest effect with the average effect coefficient of -0.0038 (Figure 7) . The effect of spatial extension of temperature components on the rate of precipitation shows that around 55.84 percent of the areas in Iran have been under the effect of minimum temperature components, 33.55 percent under the effect of temperature indices and around 11.61 percent under the effect of maximum temperature components (Figure 8). Among the minimum temperature components, the highest effect of trend was related to average minimum temperature with average effect coefficient of 0.986 (Figure 9). The effect trend of maximum temperatures on the rate of precipitation shows that northeast and east of Iran have been under the effect of maximum temperature components (Figure 10). The effect trend of temperature indexes on the rate of precipitation shows that west and southwest of Iran have been under the effect of temperature indexes components (Figure 11). In studying the indirect effects of temperature components on Iran precipitation, two of the elements, namely annual average temperature and daily temperature had significant effects in view of the three components, that is, maximum temperature components, minimum temperature components and temperature indices. The highest rate of variations in the indirect effects of temperature components on Iran precipitation is related to maximum temperature components with variations effect coefficient of 3.256 related to daily temperature and its minimum rate is related to daily temperature component with variations effect coefficient of 0.863 and the annual average temperature (Figure 12). About 1 percent of the areas in Iran is under indirect effect of maximum temperature components, 13.6 percent under the indirect effect of temperature indices and 85.4 percent under the indirect effect of minimum temperature components [61,62]. |
| Conclusions |
| Using an SEM-PLS-GIS tool – especially one with a graphical- quantitative editor that allows the user to specify the model by drawing it on curtain – it is quite easy to add climatic elements to a structural equation model. A primary purpose of our study was zoning of temperature effects on precipitation. Our other aim was to examine the effects of the three causal indicators, composite indicators, and covariates. In this study, the direct, indirect and total effects of temperature on precipitation in Iran were studied. 14 variables were investigated using a structural model. Results indicated that there are six major temperature variables that affect precipitation in Iran .The findings of this study also indicated that among the three temperature factors which were influential on precipitation, the minimum temperatures factor had the highest effect on the rate of precipitation .The hypothesis for the effects of the minimum temperature mean, lowest temperature records, maximum temperature mean, highest temperature records, dew point temperature and daily temperature on the rate of rainfall in Iran is also accepted. After all, the analysis of the temperature effects on the rate of precipitation in Iran through the SEM-PLS-GIS method can show the magnitude of these effects on the rate of precipitation changes and can well examine the variation patterns. |
References
|
Tables and Figures at a glance
| Table 1 | Table 2 | Table 3 | Table 4 |
| Table 5 | Table 6 | Table 7 |
Figures at a glance
 |
 |
 |
 |
| Figure 1 | Figure 2 | Figure 3 | Figure 4 |
 |
 |
 |
 |
| Figure 5 | Figure 6 | Figure 7 | Figure 8 |
 |
 |
 |
 |
| Figure 9 | Figure 10 | Figure 11 | Figure 12 |
Relevant Topics
- Atmosphere
- Atmospheric Chemistry
- Atmospheric inversions
- Biosphere
- Chemical Oceanography
- Climate Modeling
- Crystallography
- Disaster Science
- Earth Science
- Ecology
- Environmental Degradation
- Gemology
- Geochemistry
- Geochronology
- Geomicrobiology
- Geomorphology
- Geosciences
- Geostatistics
- Glaciology
- Microplastic Pollution
- Mineralogy
- Soil Erosion and Land Degradation
Recommended Journals
Article Tools
Article Usage
- Total views: 15785
- [From(publication date):
specialissue-2015 - Aug 16, 2025] - Breakdown by view type
- HTML page views : 10995
- PDF downloads : 4790
