Special Issue Article Open Access
Cable Shovel Stress & Fatigue Failure Modeling - Causes and Solution Strategies Review
Muhammad Azeem Raza* and Samuel FrimpongMissouri University of Science & Technology, Rolla, MO, USA
- *Corresponding Author:
- Muhammad AzeemRaza
Missouri University of Science & Technology
Rolla, MO, USA
E-mail: muhammad.raza@mst.edu
Received Date: January 15, 2013; Accepted Date: January 17, 2013; Published Date: January 26, 2013
Citation: Raza MA, Frimpong S (2013) Cable Shovel Stress & Fatigue Failure Modeling - Causes and Solution Strategies Review. J Powder Metall Min S1:003. doi: 10.4172/2168-9806.S1-003
Copyright: © 2013 Raza MA, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Powder Metallurgy & Mining
Abstract
Cable shovel is a primary excavation unit in many surface mines around the world. The capacities of the shovels have seen an ever increasing trend to achieve the economies of large scale operation. The modern day shovels have 100+ tons per pass production capacities. The dynamic force of 100+ ton material combined with the dynamic cutting, friction and acceleration forces during the excavation result in severe stress loading of the shovel front end components. Stress and fatigue cracks appear, as a result of this cyclic stress loading, resulting in expansive breakdown of shovel components. Numerical and analytical techniques can be used to model the stress and fatigue failures. This paper outlines the causes and some of the strategies to model stress and fatigue failure of shovel components and to predict shovel component life.
Introduction
Material excavation is the primary activity in surface mining operations; and shovel excavators are the primary production equipment in mining industry. The active population of cable shovels is about 2400 units around the world out of which 1700 are 20mt or larger capacity (http://parkerbaymining.com/mining-equipment/ electric-shovels.htm). Joy Global (P&H), Caterpillar (formerly under Bucyrus) and OMZ(IZ-KARTEX) are the largest electric shovels OEM around the world. The cable shovel is the preferred equipment for excavating larger capacities economically over its economic life. The capital investment in cable shovels can be as high as $25 million. The efficiency of the overall surface mining operations, where shovel-truck system is the primary mining system, is largely dependent on shovel efficiency. There is a trend in the mining industry towards excavating and loading more tons per scoop to achieve the economies of scale and reduce per ton excavation and haulage costs. There has been an increasing trend in cable shovel capacities as the capacity improved from 5yd3 in 1960 to 44+ yd3 today. Modern day cable shovels have the payload capacities of 100+ tons per scoop. The excavation of 100+ tons per scoop, combined with the weight of the dipper, and diggability variation of the formation result in varying mechanical energy inputs and stress loading of the boom and dipper-and-tooth assembly across the working bench. Furthermore, the repeated loading and unloading cycles of the shovel induce fatigue stresses in the shovel components. The induced stresses over time may exceed the yield strength of steel/ material of the shovel leading to fatigue failure, teeth losses, and boom and handle cracks. These frequent breakdowns result in increased shovel downtime, reduced efficiency, higher repair costs, and increased production costs.
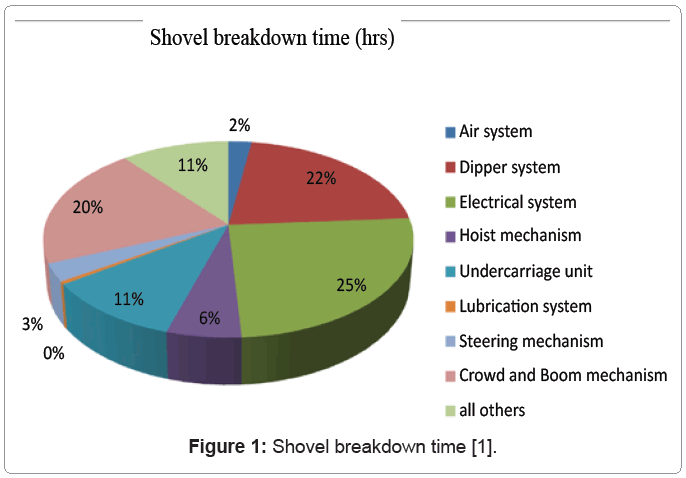
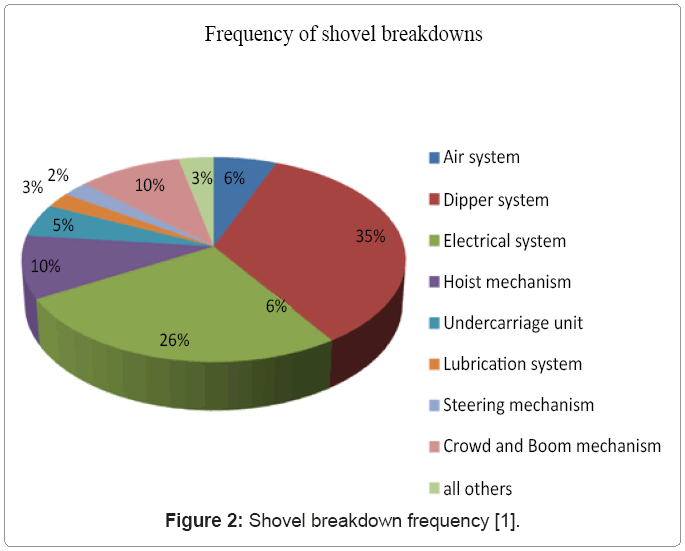
Majority of the shovel downtime is dipper related. Roy et al. [1] reported the dipper related problems to be the 2nd largest contributor towards shovel breakdown time as shown in figure 1. The data also show that dipper related breakdowns were the most frequent amongst all the breakdowns as shown in figure 2. Knights [2] reported a teeth set interval time of four days at Morenci mine, costing around US$3,000 per set for planned replacement. The cost of unplanned change-out of tooth set was estimated at US$41,368 during the study period of approximately a year. Pearson et al. [3] reported the sudden breaking down of the boom of a large barge mounted hydraulic excavator due to fatigue cracks reaching the critical length. Many times the broken teeth of the excavator end-up in the crushers resulting in crusher breakdown and increased repair costs. Understanding and estimating the stresses on teeth and dipper assembly is, therefore, very critical towards estimating the economic life of these components and avoid the costly downtimes and related problems.
The current practice for the shovel front-end assembly repair is generally based on experience and history rather than science. This leads to frequent and costly shovel breakdowns. A systematic study is required to model the dynamic stresses during the digging to understand the failure mechanism and quantitative assessment of the failure.
Solution Methodology
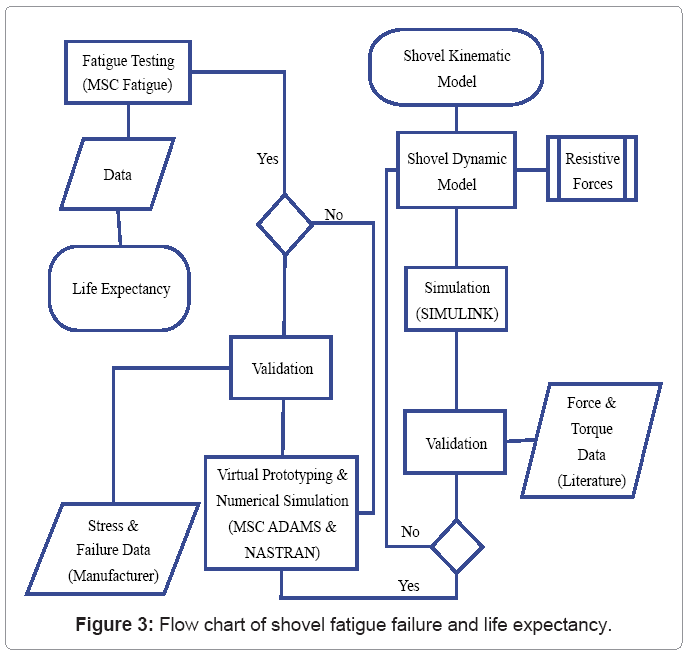
To have a systematic study for shovel stress and fatigue failure modeling, a detailed understanding of the shovel working and its interaction with the formation is required. Figure 3 shows a flowchart for such a study and to determine the life expectancy of shovel front-end components for known defect or assumed cracks. Understanding and modeling the stresses on the shovel components is the first step towards this study. A dynamic model of the shovel is essentially required to model the stresses. A critical component of this shovel dynamic modeling is to model the shovel-formation interaction incorporating the dynamic resistive forces during the digging. A validated dynamic model can lead to a virtual prototype of the shovel front-end assembly measuring the stresses during the normal duty cycle of the shovel. The stress level history data generated through these virtual prototypes, combined with the finite element modeling of the shovel components, can be used to estimate the life expectancy of the shovel front-end components for assumed or known cracks.
Cable Shovel Nomenclature and Working
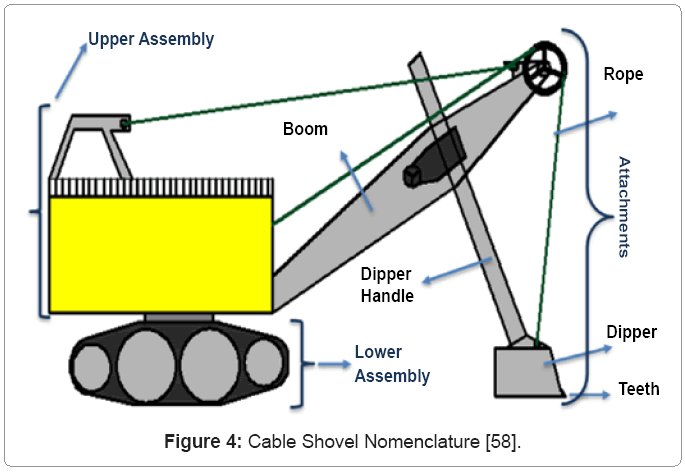
Figure 4 illustrates a schematic view of a cable shovel. A cable shovel consists of three major mechanisms: the lower, upper and the attachments. The lower assembly consists of the propel drive and crawler system and provides a solid and stable base for the excavator. This helps relocating and repositioning the excavator against the face. The shovel’s upper assembly is a roller and center-pin mounted on the lower mechanism. The upper assembly consists of multiple decks with housing for the hoist and swing machinery and electronic control cabinet on the lower deck; and the operator’s cab on the upper deck. Additionally the upper assembly provides a platform for boom attachment and counter weight for the dipper. The attachment consists of the boom, crowd machinery, dipper-handle, dipper and ropes.
The primary motions of a cable shovel include propel, swing, and crowd/retract. The shovel uses the propel function to tram from one digging site to another and to position itself against the face. Shovel swing motion, between excavation face and haulage equipment, is controlled through multiple swing gears, pinions and electric circuits. Dipper, dipper teeth, dipper handle and ropes are the important components of shovel front-end assembly.
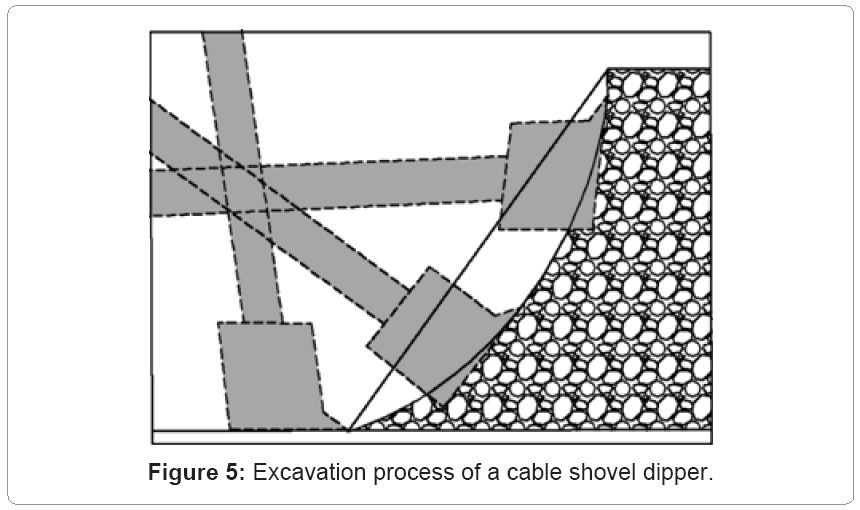
Figure 5 shows the digging operation of the duty cycle of cable shovel. The digging cycle starts with the crowding motion of the dipper along the surface of the ground and then hoisting through the formation. A good digging practice involves the penetration of dipper enough into the formation to fill the bucket completely closer to the top of the bench i.e., avoiding the filled bucket moving through the formation. Dynamic weight and excavation forces act on the shovel as the dipper moves through the formation. In the topics below we review the resistive forces acting on the shovel dipper, followed by the methodologies for dynamic modeling of the shovel, and the fatigue life expectancy of the shovel front-end assembly.
Formation Resistive Forces
The excavation process with a tool can be categorized as penetration, cutting, and scooping processes [4,5]. In general terms, penetration is the insertion of the tool into the medium; and cutting is the lateral movement of the tool, generally at a constant depth. The resistive force and soil failure theories date back to the research efforts by Coulomb [6] and Mohr[7] resuling in simpler mathematical formulation for shear failure. Ninteenth century saw a significant work and development in the soil failure theories, especially for soil cutting using tools; and 2D and 3D failure models are avaialble based on imperical, analytical, andFEM and DEM techniques.
The soil-tool interaction and resistive forces depend on a number of tool, soil and operating parameters. Hemami and Hassani [8] listed 32 parameters (tool, medium, operation, environment, and tool-medium related) that were considered in the cutting and excavation models by different researchers. The high frequency tool parameter was the tool width (w), while high frequency soil parameters included cohesion (c), angle of internal friction (φ) and bulk density (γ); and high frequency operating parameters included cutting angle (α), tool velocity (v), depth of cut (d), and surcharge (q) [4].The basic assumptions in almost all the models are the homogeneity, continuity, and isotropy of the medium in front of the tool [9-12]. Blasted or fragmented rock, as found in many mining operations, can be considered as homogeneous and continuous material when excavated with narrow tools [13]. Exceptions do exist; however, in general the variability is low in mined rocks.
Terzaghi [14] presented a theory for the bearing capacities of soils for shallow foundations based on passive earth pressure theory, equation1. The model is important as it formed the basis for Universal Earthmoving Equation (UEE).
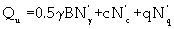 (1)
(1)
Osman [15] and Reece [16] based their excavation models, realizing the similarities between the two, on Terzaghi’s bearing capacity model. The fundamental equation for earthmoving or UEE was first introduced by Reece [16] as given in equation (2).
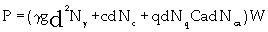 (2)
(2)
The most complete form of the UEE can be summarized as [10] as in equation3, with a dynamic term to account for speed of the tool:
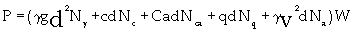 (3)
(3)
The N-factors here depend upon the soil properties, tool geometry, and tool-soil interface; and in simple cases may be determined analytically. The above 2D models are based upon passive earth pressure theory or limit equilibrium techniques. The models assume an instantaneous failure, which is true for most plastic soils. The failure for soils, e.g., cohesive soils, can be progressive failure as well. Yong and Hanna [17] applied FEM techniques to analyze soil cutting to account for the progressive failure of soil at the tool tip. The model was a 2-D model and used plane strain conditions. Their experimental and predicted results matched closely under the experimental conditions. FEM techniques assume material as a continuum, while, soil and fragmented rocks are discontinuous medium and undergo larger displacements at pre-defined planes.
Cundall and Strack [18] introduced a DEM method to analyze discrete particle assemblies. In DEM the medium is considered as an assembly of discrete particles connected through a spring to represent the elastic/in-elastic properties of the medium. DEM has been used to model soil cutting by different tools and cutting conditions [19-23]. DEM analyses are generally limited to small scale studies. The actual soil cutting process consists of billions of particles which require huge computational resources for real simulation experiments. Further, the particles and contact are generally simpler, while the actual grain geometries and contacts are complex in nature.
Digging with a cable shove dipper is 3-dimensionl in nature, where the side plates also take part in excavation. There exist few 3-D extensions of 2D soil cutting models [10,24,25].
Shovel Resistance Forces and Modeling
A cable shovel dipper has teeth at its front end as the cutting tools and the excavation process is a combination of penetration, cutting, and scooping (bucket filling) as shown in figure 5. When cutting by a blade, the cutting force is generally decomposed into two orthogonal components: (i) tangential force component acting along the blade surface, and (ii) normal force acting perpendicular to the blade surface. For excavation with a dipper, the teeth, lips, and side plates all take part during the digging process. Resistance offered by soil on cutting tool forms the basis for resistive force theories or models on excavator. The resistive forces acting on the dipper of a shovel during the digging operation are a combination of cutting forces at the teeth and lip and the excavator, and excavation forces due to material movement along, ahead, and inside the dipper. There have been attempts to model these forces, both experimentally and analytically. Some of the earlier work was carried out by Russian researchers.
Dombrovskii and Pankratov [26] proposed the tangential force to the digging of soil, P, as the sum of three component forces – soil’s resistance to cutting; frictional resistance of the tool with soil; resistance to movement of the drag prism ahead of the tool and the soil movement inside the bucket (Alekseeva et al. [27] given in equation 4. They proposed another simplified model as given in equation 5.
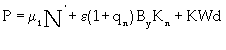 (4)
(4)
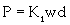 (5)
(5)
Here k1 was the specific digging resistance which, unlike the specific cutting resistance k, includes the cutting and all other resistances. The values for k and k1 were calculated experimentally for different kind of soils.
Balovnev [9] extended the UEE and the passive earth pressure theory to model the forces on a bucket by dividing the forces into individual constitutive components (side walls, front blade, back of bucket). Balovnev[9] proposed the total excavating effort as the sum of all the forces on individual parts. The four individual forces were identified (P1- P4).
Zelenin et al.[12], after extensive experimentation, proposed models and came up with the following empirical formulae (equation 6) for the cutting resistance, P for unfrozen soil with a bucket without teeth.
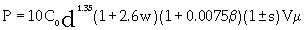 (6)
(6)
Zelenin et al. [12] postulated that for soil cutting with a bucket with teeth, the teeth eliminated the participation of side plates during cutting; therefore, the cutting force for a bucket with teeth was as modified into equation 7.
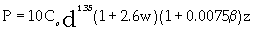 (7)
(7)
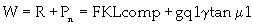 (8)
(8)
Where z is the coefficient taking into account the effect of blades. Zelenin et al.[12] gave a graph to calculatez values depending upon the ‘w’ and ‘d’. The information in table 1 can be approximated from that graph. The ‘z’ values increase with decrease in ‘d’values and were calculated for d=25cm to d=5cm. The coefficient z also depends upon the ratio of a’/b’ (where a’ being the spacing between teeth and b’ being the width of tooth). Table 2 gives the multiplying factors for z based on ratio a’/b’. Zelenin et al. [12] further developed the model (equation 8) for the forces during excavation process and divided the excavation forces into two categories: forces due to longitudinal compression of soil chip (R) and forces due to movement of drag prism ahead of bucket (Pn).
| Length of horizontal surface (w, meters) | 0.25-0.50 | 0.50-0.75 | 0.75-1.00 | 1.00-1.25 |
| Coefficient z | 0.55-0.75 | 0.63-0.78 | 0.69-0.78 | 0.72-0.82 |
Table 1: Dependence of z on d and w.
| Ratio a'/b' | a'=b' | a'=2b'-3b' | a'=4b' | a'=5b' |
| z | 1.2 | 1 | 1.1 | 1.25 |
Table 2: Dependence of z on a/b [12].
Zelenin et al. [12] postulated that these forces were present for buckets with teeth for graders and draglines.However, they were absent for bucket with teeth for a cable shovel, teeth disintegrate the soil in front of the bucket and there is no drag prism. Therefore, the total excavation force for the shovel bucket with teeth was as given in equation 7[12]. It must be noted that these empirical results came from a large number of experiments with smaller buckets. Given the dipper sizes today, the results might change.
Wu [28] used a resistance model based on the resistive forces acting on the dragline bucket proposed by Rowland [29]. The forces on the dipper were divided into four components – payload weight; friction forces on teeth; friction forces on lip; and four frictional forces on dipper surfaces (outer dipper bottom, inner dipper bottom, outer surfaces of side plates, and inner surfaces of side plates). The frictional forces of the bottom surface, inner and outer, were modeled based on the total payload which increased linearly with position. The frictional forces on the side plates (inner and outer) were calculated utilizing the passive earth pressure theory on a wall. The teeth and lip forces were modeled based on Hettiaratchi and Reece [30]. The payload was modeled as the maximum payload capacity of the dipper. All these forces were considered as static forces acting at the tip of the dipper.
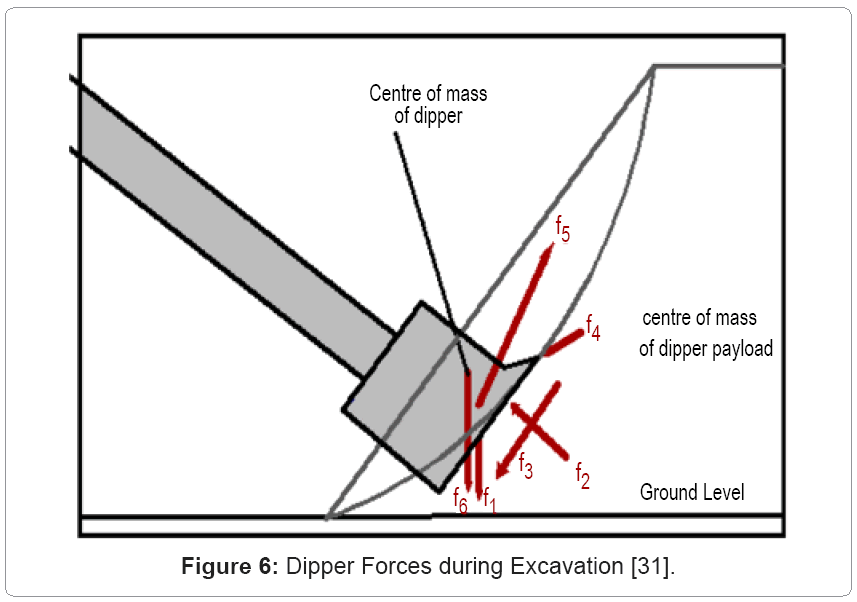
Hemami [31], in an attempt to automate the LHD loading, proposed a model consisting of five component forces (f1-f6), which must be overcome, on a dipper during excavation as shown in figure 6. Force f6was originally defined as a part of f1.Hemami[31] defined the f1 and f5 as the dynamic forces, where f1 changes both in magnitude and the point-of-application and f5 depends upon the acceleration of the bucket. Further, the force f6 was defined as a part of f1 and f6. The force f6 cannot be made a part of f1 and f5 as the point of application of f6 is not concentric with f1. Hemami [31] modeled f1 using geometric configuration, velocity, position and orientation of the bucket. The geometric assumptionsfor calculating the center of mass of material inside the bucket may not be valid for the shovel dipper.This is due to the fact that the bucket considered had a triangular shape while the modern shovel dipper is more rectangular in shape.
Takahashi et al. [32] used a similar description for the resistive forces (f1-f5) on the bucket of a LHD. Forcef6 was modeled as part of f1. The forces f1 and f3 were calculated geometrically using the bucket orientation and soil properties, and f4 was calculated by solving the force balance equations using the static earth pressure on the particles. A small scale model was used to compare the experimental and calculated forces. The model, however, was not tested for the larger buckets and forhigher penetration rates.
Awuah-Offei et al. [33] kept the same six forces as proposed by Hemami[31] and modeled the force f1 and f3. Forcef4was modeled as a part of f3. Force f1 was modeled as a dynamic force as given in equation 9.
f1 = Aωγg (9)
The cross-sectional area A was calculated as equation10.
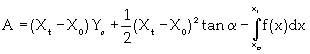 (10)
(10)
Where x0, y0 were the initial coordinates of the tip of the dipper when it comes in contact with the material and xt is the x co-ordinate after a time t. The integral in the above equation defined the area under the trajectory curve and is numerically calculated once the points on the trajectory of the curve are known.
Forces f3 and f4were modeled based on the forces defined by Balovnev [9] model using the passive earth pressure theory. A numerical model was created to calculate the forces on the dipper while it moves through the muck pile. The model, however, doesn’t give the forces for shovel joints and links that are important to compare against the strength, yield and fatigue behavior of the shovel.
Summary of Resistive Forces
Shovel excavation is complex in nature. There have been several attempts to model the resistive forces; however, no model describes the model completely. Some of the recent comprehensive models made the following assumptions:
• The modelsare two-dimensional, while the dipper width is incorporated later in the model.
• The material failure plane is flat. [31,32]
• The material is homogenous. [31,32]
• The thickness of the bucket is negligibly small compared with the size of the rock pile. [32]
Hemami [31] model, consisting of six forces (f1- f6), is by far the most comprehensive model. All these forces, except f6 are dynamic in nature. Research shows that f1 and f4 are the most important and dominant forces for shovel digging [31,32]. The excavation research generally ignored the dynamic nature of the resistive forces especially for f1.
Hemami [31] and Awuah-Offei et al. [33] modeled f1. Awuah et al.[33]’s model is easier to compute for simpler dipper trajectories. The force f2 can be set to zero, provided the bottom of the bucket stays clear of the material and does not compress the material by selecting a proper trajectory of the bucket (Hemami, [31]). Several models exist to estimate the cutting force of soil by bucket type dippers. Only Zelenin et al.[12] empirical model considers the teeth ahead of the bucket; therefore, f3 can be modeled as a part of f4 using Zelenin et al. [12] model[31,33].The force f5 can be set to zero if we assume that the dipper moves with a constant speed through the muck pile [33]. Force f6 is a known force as it depends on the dipper dimensions and the material being excavated. It is simply the weight of the bucket.
Kinematic and Dynamic Modeling
One of the early developments on the excavator kinematics, for an automatic or semiautomatic backhoe, are described in Seward et al. [34].Kinematic relations were developed, for both forward and reverse, between the joint angles and the position of the bucket. This work was primarily based on the geometric relationships between the different links.
Koivo [35] produced a good texton the robotic manipulators.He described the principles and strategies for kinematic and dynamic design of robotic manipulators. Koivo [36] later presented a detailed kinematic model for backhoe excavator using the Denavit and Hartenberg [37] notation. In that research, Koivo [36]gave a detailed description of the scheme for the coordinate frame assignment and the estimation of structural kinematic parameters. The forward and reverse kinematic equations for the backhoe were developed using the Newton-Euler formulations. He presented a very fundamental background for the kinematics of the loaders, which is a great research referencein the field of kinematic analysis of excavators.
Vaha and Skibniewsky [38] used Newton-Euler equations of motion to produce a dynamic model of the excavator. They preferred Newton-Euler motion equations over Lagrange energy equations because of computational ease and effeciency for being recursive in nature. The dynamic model didnot, however, consider the external resistive forces which are very important aspect for the complete dynamics of an excavator.
Koivo et al. [39] extended the earlier work Koivo [36] and presented a dynamic model for the excavators (backhoe). The model comprises of detailed kinematic and dynamic equations for the backhoe using Newton-Euler recursive techniques. The desired trajactories were computed using simulation studies done in C language programming environment. The resistive forces were also included based on Alekseevaet. al. [27].
Hendricks et al. [40] developed the kinematic and dynamic model and simulator of cable shovel to improve the shovel productivity using Lagrangian formulations. Daneshmend et al. [41] later applied the iterative Newton-Euler formulation to the same kinetic model and developed the dynamic model. This later approach is considered better being iterative and for easier computer programming. The work, however, did not consider the crowd action of the arm which is very important for complete description of the dynamic behavior of the cable shovel. In addition, no model predictions were presented in these papers.
Wu [28] developed a five-link full-body dynamic model of the cable shovel using Newton-Euler equations. The author used a resistive force model of Rowland [29], developed for dragline bucket filling, as the forces on cable shovel dipper. The forces were assumed to be acting at the tip of the dipper as well.
Frimpong et al. [42] used the Newton-Euler method to build the dynamic model of the cable shovel front-end assembly for shovel-formation interaction studies as given in equation 11and12. The formation resistive and breakout forces were based on the Zelenin et al. [12] model. The breakout forces were considered to be acting at the tip of the excavator. The model only considered the shovel breakout forces and ignored the dynamic forces of material inside the dipper, the dipper itself, and the reaction forces. A simulated study calculated the joint torque and force during a 3-seconds digging cycle.
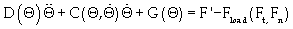 (11)
(11)
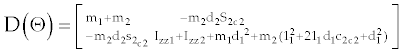
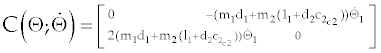
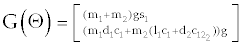
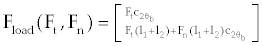 (12)
(12)
Frimpong and Li [43] modeled the cable shovel using Lagrange formulations to study the boom stresses for oil-sands excavation. The cable shovel was modeled as a seven bar linkage and the full multi-body simulations were created in ADAMS/NASTRAN software. No separate resistive model was used; rather the in-situ digging environment for oil-sands was modeled as continuous media using a spring-dashpots system. The virtual prototype was created to test the two oil-sands material digging cases. The 3-seconds simulations revealed that the Von-Mises stresses at three nodes of the booms are critical and might exceed the yield strength of the dipper.
Li and Frimpong [44] extended the research [43] and performed rigid and flexible body analysis in ADAMS/NASTRAN and ADAMS/FLEX softwares. The hybrid virtual prototype simulated the in-situ digging conditions as described in previous research [43] to calculate the Von-Mises stresses for shovel components. Frimpong et al. [45] advanced the shovel component stress analysis research [43,44] for in-situ oil-sand excavation to three different cases. The research found that six nodes received the maximum stress in all the three different cases studied and the stress values were critical for low-carbon and the lower end of the medium-carbon steel. The researchers also suggested that the boom stresses could be used to assess the efficiency of the operator towards better training.
Awuah-Offei [46] utilized Newton-Euler based vector loop equations for dynamic modeling of the front-end of shovel dipper. The model calculated the hoist force for the dipper by incorporating the dynamic weight and excavation forces as the dipper moved through the muck pile. The vector loop equations, however, don’t calculate the joint torques and forces as the vector lengths didn’t exactly match with the geometric lengths of the dipper.
Summary of Kinematic and Dynamic Models
The literature review shows that both Newton-Euler and Lagrange formulations are commonly used for kinematic and dynamic modeling of the cable shovel. However, Newton-Euler equations of motions are preferred for modeling of the excavators being computationally easier and recursive in nature that helps in computer implementation.
In general, the forces acting on the dipper were greatly simplified; and generally limited to cutting forces only. The dynamic nature of the weight and cutting forces is generally ignored. Similarly, the research didn’t model the stresses on the dipper surfaces, teeth and ropes.
Fatigue Failure Modeling of Excavators
Cable shovel excavation is cyclic in nature. The stresses on the front-end assembly continuously vary during an excavation duty cycle of cable shovel [45,46]. This stress loading results in fatigue cracking of shovel components leading to expensive repairs, increased shovel down-time, and possible failures. Pearson et al. [3] reported a sudden breaking down of the boom of a large barge-mounted hydraulic excavator due to fatigue cracks reaching the critical length.
Metal Fatigue is a complex metallurgical phenomenon and depends on microstructure of the metal. External factors e.g. environment, temperature etc. impact the metal fatigue properties and toughness. A cable shovels; therefore, with similar stress levels in one operation might experience brittle fracture failure in freezing conditions. Cable shovel, like all other engineering structures, is designed to withstand the normal elastic stress levels. However, the internal material flaws and welded joints may expand rapidly to undesirable lengths under cyclic loading condition leading to failure. The current practice for crack repairs is based on experience rather than on scientific principles. Fatigue analysis is used to assess the damage and take concrete actions to rectify the problems early for machine health and longevity. It is important to understand the fracture growth rates at different areas of the shovel for better shovel health and longevity. Metal fatigue has been a subject of interest for design engineers and there are a number of good texts available. One of the good texts is produced by Bannantine et al. [47].
There are three common fatigue failure analysis approaches– stress-life approach; strain-life approach; and fracture-mechanics approach; and all have their own application with overlapping boundaries. Stress-life approach is generally represented by a Stress-Number of cycles to failure (S-N) curve as defined by Anon [48]. The technique is generally suitable for high cycle fatigue components where material behavior is elastic i.e. stress-strain levels stay within elastic limits.
Strain-life approach is best suitable for high stress, low cycle fatigue, where stress-strain behavior is plastic. The engineering structures are generally designed to keep the stress ranges within elastic limits. However, there are generally left few notches due to internal material flaws, and welding points. The stress levels around these notches can be well above the elastic ranges and can fall in the plastic ranges. Every fatigue failure has two crack related phases –crack initiation and crack propagation. The distinction between two phases is almost impossible to make. However, it is believed that fatigue life is more spent during the crack propagation. The plastic behavior around the notches can be attributed as the crack-initiation phase. Standardized procedures and recommendations are available for testing and fatigue life prediction [49,50] based on strain-life approach.
Fracture mechanics approach is used to estimate the propagation life of a crack. For these approaches the initial crack lengths are either known (welds, known defects, porosities, cracks found during non-destructive testing etc.) or assumed. A combination of strain-life and fracture mechanics approach can be used for crack initiation and crack propagation lives, to estimate the total fatigue life of a component; which in this case will be a sum of lives estimated by strain-life approach and by fracture-mechanics approach.
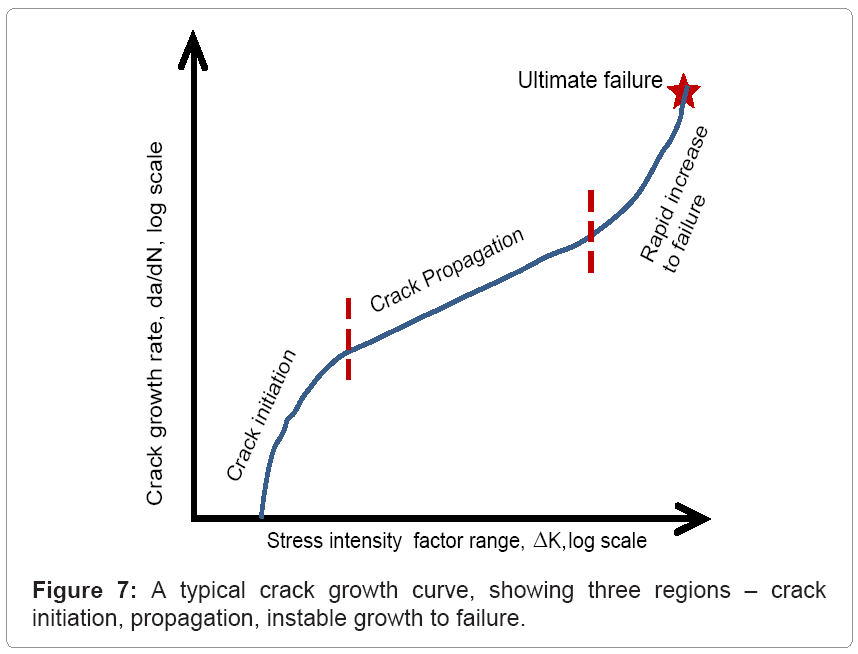
A typical crack growth curve is shown in figure 7. Three regions can be identified on this curve: crack initiation, crack propagation (region-II), and rapid increase in crack growth leading to failure. Crack propagation is relatively linear and the slope of this curve defines the crack growth rate. The majority of lifeof a crack is spent during this stage, and different models are available for region-II of this curve. One of the most commonly used methods is given by Paris and Erdogan [51] and is known as Paris Law (Equation 13).
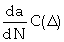 (13)
(13)
The material constants (c, m) can be found for different metals in literature or obtained using standard tests i.e. ASTM E647.
The stress intensity factor ‘K’ defines the magnitude of local stresses around the crack tip and can be defined as in equation14 [47].
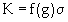 (14)
(14)
Stress intensity factors are available for simple crack geometries in literature and can also be computed numerically [52-55].
The fatigue life can then be computed for a known length crack by integrating the equation 15 [47].
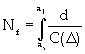 (15)
(15)
There is no reported work for fatigue life estimation of cable shovel dipper and front-end assembly. The only reported work is done by [56-58] who estimated the fatigue life for corner cracks in the steel welded box section of the shovel boom. The researchers used finite element method to estimate the crack growth rate, and metal properties were found in the lab using standard procedures.
Conclusions
Cable shovel front end assembly undergoes severe stress loading during the excavation process, given the present day capacities. The stress loading results in stress and fatigue failure of the shovel components, resulting in shovel downtime, expensive repairs and reduced efficiencies. To model the fatigue failure and estimate the lives of the shovel front-end components a systematic and detailed dynamic and stress modeling of the shovel is required. A key component of this modeling is the shovel-formation interaction and a dynamic model that incorporates all the resistive forces during the excavation process. Virtual prototyping combined with finite element modeling techniques can be utilized to estimate the stresses loading of shovel front-end assembly. Once the stress modeling is done, numerical techniques can be used to find the fatigue properties of the material and hence the life of the components can be estimated.
Nomenclature
| τ | shear strength |
| c | cohesion |
| φ | internal friction angle of the soil |
| C | material constant for Paris Law |
| Ca | coefficient of adhesion between soil and tool |
| Co | the number of impacts required to sink a cylindrical tip in a standardized test by 10 cm.(Zelenin, Balovnev, & Kerov, 1985) |
| ρ | the angle that the rupture surface makes with the horizontal |
| s | thickness of side plate of bucket |
| V,μ | coefficients dependent upon the cutting conditions for (Zelenin et al., 1985) model |
| β | tool cutting angle |
| q | surcharge pressure acting vertically on soil surface |
| d | tool working depth |
| w | width of tool |
| γ | bulk density |
| Nγ', Nc', Nq' | N-Coefficients for Terzaghi’s model. Valued depend upon the internal friction angle (φ) |
| Nγ, Nc, Na, Nca, Nq | N-factors in the Universal Earthmoving Equation |
| z | coefficient for teeth configuration in the Zelenin model |
| Qu | ultimate bearing capacity of rock, as defined in Terzaghi’s Equation |
| B | width of foundation |
| FEM | Finite Element Modeling |
| DEM | Discrete or Distinct Element Modeling |
| μ1 | coefficient of friction between material and bucket |
| N' | Normal force |
| ε | coefficient of resistance to filling of the bucket and movement of the drag prism of soil |
| qn | ratio of the volume of the drag prism ahead of bucket to the volume of the bucket |
| Bv | volume of bucket |
| kn | ratio of the volume of the drag prism ahead of bucket to the volume of the bucket |
| k | specific cutting resistance of soil |
| P1 | cutting resistance of the blade |
| P2 | additional resistance due to wear of the edge |
| P3 | resistance offered by the two sides |
| P4 | (resistance due to friction of the sides |
| Kcomp | specific resistance of the given stratum to longitudinal compression, (N/cm2) |
| F | stratum cross-section (w*d) |
| g | gravitational acceleration (m/sec2) |
| q1 | volume of drag prism (m3) |
| γ | is density of soil (kg/m3) |
| f1 | Force required to overcome the weight of the loaded material in and above the bucket. |
| f2 | Resultant of forces of resistance for material moving towards the bucket. |
| f3 | Force due to the friction between the bucket walls and the soil material sliding into the bucket. |
| f4 | Resistance to cutting and/or penetration acting at the tip of the bucket and side walls. |
| f5 | Inertia force of the material inside and above the bucket. |
| f6 | force required to move the empty bucket (modeled as part of f1) |
| A | Cross-sectional area swept by the dipper up to failure plane |
| f(x) | function defining the failure plain (curve) |
| ω | dipper width |
| da/dN | crack growth rate with every cycle as defined by Paris Law |
| a | crack length |
| N | Number of cycles to failure |
| K | Stress intensity factor |
| m | Material constant for Paris Law |
| σ | remote stress |
| f(g) | correction factor depending upon the material and crack geometry |
| ai, af | Initial and final/critical known/assumed crack length |
| C(Θ,Θ) | Generalized Coriolis and centripetal torque |
| D(Θ) | Generalized inertia matrix |
| G(Θ) | Generalized gravity torque |
| m1, m2 | mass of crowd arm and dipper, respectively |
| l1 | length of crowd arm from pivotal point to connection point between arm and dipper |
| l2 | Length between dipper tip and connect point of arm and dipper |
| si, ci | Sinθi and cosθi, respectively |
| di | Offset distance of the gravity centre in link i |
| Izz, Izz2 | Moment of inertias of crowd arm & dipper |
| Fn, Ft | normal & tangential cutting resistive forces on dipper tip |
| F' | Cable shovel breakout force |
| Fload(Fn, Ft) | formation resistive forces |
References
- RoySK, BhattacharyyaMM,NaikanVNA(2001)Maintainability and reliability analysis of a fleet of shovels. Mining Technology 110: 163-171.
- KnightsPF(2009)Optimal Replacement Intervals for Shovel Dipper Teeth. International Journal of Mining, Reclamation and Environment23: 157-167.
- PearsonJ,HannenW,SoderbergE(2004)Development of fatigue monitoring system for a hydraulic excavator. Pract Period Struct Des Constr 9: 221-226.
- BlouinS, HemamiA, LipsettM(2001)Review of Resistive Force Models for Earthmoving Processess. JAerospEng14: 102-111.
- LipsettMG,MoghaddamY(2011) Modeling Excavator-Soil Interaction. Bifurcations, Instabilities and Degradation in Geomaterials0: 347-366.
- Coulomb CA (1776) Essai Sur Une Application Des REgles Des Maximis et Minimis a Quelques Problems de Statique Relatifs a l'architechture. Academic Royale des Sciences: Memories de Mathmatique et de Physique, presentes a l'Acaemie Royale des Sciences, par Divers Savants, et lus dans les Assemblees, Paris, 7: 343-382.
- Mohr O (1914) Die Elastizitatsgrenze und Bruch eines Materials. Z Ver Dtsch Ing 44: 1524.
- Hemami A, Hassani F Procedure Design for Experiments Towards Modeling of the Cutting Force in Excavation of Bulk Media.
- Balovnev VI (1983) New Methods for Calculating Resistance to Cutting of Soil: Amerind Publishing, India.
- McKyes E (1985)Soil Cutting and Tillage. Elsevier Science Publishers, New York, USA.
- Thakur TC, Godwin RJ (1990) The Mechanics of Soil Cutting by a Rotating Wire. J Terramechanics24: 295-305.
- Zelenin AN, Balovnev VI, Kerov IP (1985) Machines for moving the earth : fundamentals of the theory of soil loosening, modeling of working processes and forecasting machine Parameters. Amerind Publishing New Delhi,India.
- Fowkes RS, Frisque DE, Pariseau WG (1973)Materials handling research: Penetration of selected/granular materials by wedge-shaped tools (Report of investigations / United States Department of the Interior, Bureau of Mines).
- Terzaghi K (1943) Theoretical Soil Mechanics: John Wiley and Sons, New York, USA.
- Osman MS (1964) The Mechanics of Soil Cutting Blades. Journal of Agricultural Engineering Research 9: 313-328.
- Reece AR (1965) The Fundamental Equation of Earthmoving Mechanics. Symposium on Earthmoving Machinery, Institute of Mechanical Engineers, 179(Part-3F).
- Yong RN, Hanna AW (1977) Finite Element Analysis of Plane Soil Cutting. J Terramechanics 14: 103-125.
- Cundall PA, Strack OD L (1979) A Discrete Numerical Model for Granular Assemblies. Géotechnique, 29: 47-65.
- Mak J, Chen Y, Sadek MA (2012) Determining parameters of a discrete element model for soil–tool interaction. Soil and Tillage Research 118: 117-122.
- Momozu M, Oida A, Yamazaki M, Koolen AJ (2003) Simulation of Soil Loosening Process by Means of Modified Distinct Element Method. J Terramechanics 39: 207-220.
- Oida A, Momozu M (2002) Simulation of Soil Behavior and Reaction by Machine Part by Means of DEM. Agricultural Engineering International: The CIGR Journal of Scientific Research and Development, IV.
- Tanaka H, Momozu M, Oida A, Yamazaki M (2000) Simulation of Soil Deformation and Resistance at Bar Penetration by the Distinct Element Method.J Terramechanics 37: 41-56.
- Ting JM, Corkum BT, Kauffman C, Greco C (1989) Discrete Numerical Model for Soil Mechanics. J Geotech Eng 115: 379-398.
- Boccafogli A, Busatti G, Gherardi F, Malaguti F, Paoluzzi R (1992) Experimental evaluation of cutting dynamic models in soil bin facility. J Terramechanics 29: 95-105.
- Swick WC, Perumpral JV (1988) A model for predicting soil-tool interaction. J Terramechanics 25: 43-56.
- Dombrovskii NG, Pankratov SA (1961) Zemleroinye Mashiny, Ch. 1 Odnokovshovye Ekskavatory (Earthmoving Machines, Part 1 Single-Bucket Shovels): Gosstroiizdat, Moscow.
- Artem'ev KA, Bromberg AA, Alekseeva TV (1985) Machines for Earthmoving Work, Theory and Calculations: Amerind Publishing Co. Pvt. Ltd. New Delhi, India.
- Wu H (1995) Modeling and Simulation of Electric Mining Shovels. McGill University, Canada.
- Rowland JC (1991) Dragline Bucket Filling. University of Queensland.
- Hettiaratchi DRP, Reece AR (1974) The calculation of passive soil resistance. Géotechnique 24: 289-310.
- Hemami A (1994) An Approximation of the Weight of the Loaded Material During the Scooping Operation of a Mechanical Loader. Transactions of the Canadian Society of Mechanical Engineering 18: 191-205.
- Takahashi H, Hasegawa M, Nakano E (1999) Analysis on the Resisitive Forces Acting on the Bucket of a Load-Hual-Dump Machine and a Wheel Loader in the Scooping Task. Advanced Robotics 13: 97-114.
- Awuah-Offei K, Frimpong S, Askari-Nasab H (2009)Formation excavation resistance modelling for shovel dippers. International Journal of Mining and Mineral Engineering 1: 127-146.
- Seward D, Bradley D, Bracewll R (1988) The Development of Research Models for Automatic Excavation. Paper presented at the Proc. The 5th International Symposium on Robotics in Construction, Tokyo, Japan.
- Koivo AJ (1989) Fundamentals for Control of Robotic Manipulators. Jhon Wiley & Sons.
- Koivo AJ (1994) Kinematics of Excavators (Backhoes) for Transferring Surface Material. J. Aerosp. Eng 7: 17-32.
- Denavit J, Hartenberg RS (1955) A Kinematic Notation for Lower-Pair Mechanisms Based on Matricies. Trans. of ASME. Journal of Applied Mechanics 22: 215-221.
- Vaha PK, Skibniewsky MJ (1993) Dynamic Model of Excavator. Journal of Aerospace Engineering 6: 148-158.
- Koivo AJ, Thoma M, Kocaoglan E, Andrade-Cetto J (1996) Modeling and Control of Excavator Dynamics During Digging Operation. Journal of Aerospace Engineering 9: 10-18.
- Hendricks C, Daneshmend L, Wu S, Scoble M (1993) Design of a Simulator for Productivity Analysis of Electric Mining Shovels. Proc. of 2nd International Symposium on Mine Mechanization and Automation, Lulea, Sweden 329-336.
- Daneshmend L, Hendricks C, Wu S, Scoble M (1993) Design of a Mining Shovel Simulator. Innovative mine design for the 21st century: Proceedings of the International Ccongress on Mine Design, Ontario, Canada 551-561.
- Frimpong S, Hu Y, Awuah-Offei K (2005) Mechanics of Cable Shovel-fromation Interactions in Surface Mining Excavations. Journal of Terramechanics 15-33.
- Frimpong S, Li Y (2007) Stress Loading of the Cable Shovel Boom under in-situ Digging Conditions. Engineering Failure Analysis 14: 702-715.
- Li Y, Frimpong S (2008) Hybrid Virtual Prototype for analyzing Cable Shovel Component Stress. Int Journal of Manufacturing Technology 37: 423-430.
- Frimpong S, Li Y, Awuah-Offei K (2008) Cable Shovel Health and Longevity and Operator Efficiency in Oil Sands Excavation. International Journal of Mining and Mineral Engineering 1: 47-61.
- Awuah-Offei K (2005) Dynamic Modeling of Cable Shovel-Formation Interactions for Efficient Oil Sands Excavation. Missouri S&T, Rolla, USA.
- Bannantine JA, Comer JJ, Handrock JL (1989)Fundamentals of Metal Fatigue Analysis. Prentice Hall, USA.
- Anon (1871) Wöhler's Experiment on Fatigue of Metals. Engineering (London), 11.
- ASTM (1969) Manual on Low Cycle Fatigue Testing ASTM STP465. American Society of Testing and Materials, USA.
- Rice RC (1968) SAE Fatigue Design Handbook. Society of Automotive Engineers,USA.
- Paris P, Erdogan F (1963) A Critical Analysis of Crack Propagation Laws. J Basic EngD85: 528-534.
- Byskov E (1970) The calculation of stress intensity factors using the finite element method with cracked elements. Int J Fract Mech 6: 159-167.
- Parks DM (1974) A stiffness derivative finite element technique for determination of crack tip stress intensity factors. International Journal of Fracture 10: 487-502.
- Riveros GA (2006) Numerical Evaluation of Stress Intensity Factors (Ki) J-Integral Approach (Vol. ERDC/CHL-CHETN-iX-16): US Army Corps of Engineers.
- Rybicki EF, Kanninen MF (1977) A finite element calculation of stress intensity factors by a modified crack closure integral. Eng Fract Mech 9: 931-938.
- Yin Y, Grondin GY, Obaia KH, Elwi AE (2007) Fatigue life prediction of heavy mining equipment. Part 1: Fatigue load assessment and crack growth rate tests. J Constr Steel Res 63: 1494-1505.
- Yin Y, Grondin GY, Obaia KH, Elwi AE (2008) Fatigue life prediction of heavy mining equipment. Part 2: Behaviour of corner crack in steel welded box section and remaining fatigue life determination. J Constr Steel Res 64: 62-71.
- Mining PH (2003) Peak Performance Practices: Excavator selection. P&H MinePro Services, Canada.
Relevant Topics
- Additive Manufacturing
- Coal Mining
- Colloid Chemistry
- Composite Materials Fabrication
- Compressive Strength
- Extractive Metallurgy
- Fracture Toughness
- Geological Materials
- Hydrometallurgy
- Industrial Engineering
- Materials Chemistry
- Materials Processing and Manufacturing
- Metal Casting Technology
- Metallic Materials
- Metallurgical Engineering
- Metallurgy
- Mineral Processing
- Nanomaterial
- Resource Extraction
- Rock Mechanics
- Surface Mining
Recommended Journals
Article Tools
Article Usage
- Total views: 19880
- [From(publication date):
specialissue-2013 - Aug 29, 2025] - Breakdown by view type
- HTML page views : 14972
- PDF downloads : 4908