Research Article Open Access
Clinical Prediction Rule for Patient Outcome after In-Hospital CPR
Satyam Merja1, Ryan H. Lilien1 and Hilary F. Ryder2,3*1Department of Computer Science, University of Toronto, Lebanon
2Department of Medicine and The Dartmouth Institute, Dartmouth Medical School, Lebanon
3Section of Hospital Medicine, Dartmouth-Hitchcock Medical Center, Lebanon
- *Corresponding Author:
- Hilary F. Ryder, M.D
Department of Medicine and The Dartmouth Institute
Dartmouth Medical School
One Medical Center Drive
NH, 03756, Lebanon
Tel: (603) 650-8380
Fax: (603) 653-6110
E-mail: Hilary.F.Ryder@Dartmouth.edu
Received date March 16, 2015; Accepted date March 25, 2015; Published date March 30, 2015
Citation: Merja S, Lilien RH, Ryder HF (2015) Clinical Prediction Rule for Patient Outcome after In-Hospital CPR. J Palliat Care Med 5:217. doi:10.4172/2165-7386.1000217
Copyright: © 2015 Merja S, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Journal of Palliative Care & Medicine
Abstract
Abstract Background: Physicians and patients frequently overestimate likelihood of survival after in-hospital cardiopulmonary resuscitation (CPR). Discussions and decisions around resuscitation after in-hospital cardiopulmonary arrest often take place without adequate or accurate information. Methods: We conducted a retrospective chart review of 470 instances of resuscitation after in-hospital cardiopulmonary arrest. Individuals were randomly assigned to a derivation cohort and a validation cohort. Logistic Regression and Linear Discriminant Analysis were used to perform multivariate analysis of the data. The resultant best performing rule was converted to a weighted integer tool and thresholds of survival and non-survival were determined with an attempt to optimize sensitivity and specificity for survival. Results: A 10-feature rule, using thresholds for survival and non-survival, was created; the sensitivity of the rule on the validation cohort was 42.7%, and specificity was 82.4%. Conclusions: Utilizing information easily obtainable on admission, our clinical prediction tool, the Dartmouth Score, provides physicians individualized information about their patients’ probability of survival after in-hospital cardiopulmonary arrest. The Dartmouth Score may become a useful addition to medical expertise and clinical judgment in evaluating and communicating an individual’s probability of survival after in-hospital cardiopulmonary arrest after it is validated by other cohorts. Methodologically, because LDA outperformed LR in the creation of this clinical prediction rule, it may be an approach for others to more frequently consider when performing similar analysis.
Keywords
In-hospital CPR; Clinical prediction rule; Cardiopulmonary resuscitation
Introduction
Cardiopulmonary Resuscitation (CPR) was introduced in 1960 to revive victims of acute insult in otherwise good physiological condition [1]. In the past fifty years, CPR evolved from unorganized actions by untrained staff to synchronized teamwork, and has become a fundamental part of medical care for all hospitalized patients in cardiac arrest. Despite these changes, survival from CPR to hospital discharge declined from 24% in 1961 to 14% in 1981 [2]. Since 2000, the national average of survival from in-hospital cardiac arrest to hospital discharge has remained around 18% [3].
In the 1980s, responding to demands for patient autonomy, many hospitals began instituting "Do Not Resuscitate" (DNR) policies allowing patients or their families to determine that no resuscitation be attempted in the event of a cardiac arrest. However, less than 25% of seriously ill patients discuss preferences for resuscitation with their physicians [4-6]. Less than 50% of in-patients who prefer not to receive CPR have DNR orders written [7-9]. A known obstacle to the conversation is physician reluctance to discuss the issue [10,11].
Despite being asked to predict the future frequently by patients, most physicians avoid prognostication, largely because they believe they do not have sufficient information to estimate outcomes [12]. When physicians do engage in this conversation, they overestimate the likelihood of survival to hospital discharge after in-hospital CPR by as much as 300%, and they predict a success rate that is twice that actually observed [13]. This optimism strongly influences the choices of their patients. Accurate information about the probability of survival to discharge after CPR significantly alters patients’ DNR preferences [14,15] and might be helpful to patients and their physicians in deciding whether to forego this intervention.
A tool, or clinical prediction rule, utilizing pre-arrest data to estimate an individual's risk of not surviving CPR, could empower physicians to prognosticate more accurately, increase frequency of code status discussions and thereby promote patient autonomy. In the late 1980s and early 1990s, three morbidity scores, Pre-Arrest Morbidity score (PAM) [16,19], Prognosis After Resuscitation score (PAR) [20], and Modified PAM Index (MPI) [21] attempted to predict survival after resuscitation based on univariate meta-analysis (PAR), literature review (MPI) or stepwise logistic regression (PAM). However, changes in CPR algorithms, a changing and ageing population and advances in medical science in the past twenty years have led to a need to update these tools. In addition, advances in the use of computational sciences allow increasingly sophisticated multivariate and multidimensional analysis of data.
Since the creation of the “Utstein template” defining variables and outcomes essential for documenting in-hospital cardiac arrest, it has been possible to gather data in a standardized fashion. Recent studies [16-18], availing themselves of Utstein template and data collection methods, have focused on intra-arrest characteristics that are predictive of survival, but such data is not helpful to the physician or patient attempting to make a preemptive decision about use of CPR.
This study uses primary CPR data gathered retrospectively at a single center and analyzed by both linear discriminant analysis and logistic regression to attempt to determine variables predictive of nonsurvival after cardiac arrest and in-hospital resuscitation and to create a score that can be clinically useful to physicians and their patients.
Methods
Setting
We retrospectively reviewed medical and nursing records of all adult in-patient CPR attempts at our institution between January 2003 and December 2005. The center is a 389-bed tertiary care hospital affiliated with Dartmouth Medical School with average yearly admission of 20,000 patients.
Patient selection
Individuals were identified retrospectively from the CPR committee log of in-hospital cardiopulmonary arrests. Cardiac arrest was defined "the cessation of cardiac mechanical activity, confirmed by the absence of a detectable pulse, unresponsiveness, and apnea" [22]. The study cohort consisted of all consecutive patients aged 18 years and older with an in-hospital cardiac arrest and attempted resuscitation. Syncope, seizures, and primary respiratory arrests were excluded. Multiple arrests by the same individual were excluded. Patients whose resuscitation began outside of the hospital were excluded.
Assuming unequal groups (based on previous statistics, we predicted a 20% survival rate after cardiac arrest), 308 enrolled patients were needed for the study to have a statistical power of 80% to detect a significant difference with respect to history of congestive heart failure or renal failure (the only parameters with adequate published data) with a 2-sided α level of 0.05.
Data collection
A single trained chart abstractor reviewed each medical record. Admission variables were recorded on a structured data collection sheet designed for this study. We used admission variables (values obtained within 24 hours of admission) because we expect conversations about CPR and therefore the use of our rule, to take place on admission. We pre-specified all variables by developing a list of variables identified in the literature as varying significantly between survivors and non-survivors. All features were defined precisely (Appendix) prior to data collection. These criteria were adapted when possible from those used in previous investigations [23]. To minimize bias associated with the unavailability of data in patient subgroups, we imputed a value of normal when a physiologic value was missing.
The primary outcome measured was non-survival to hospital discharge. The study protocol was approved by the institutional review board of Dartmouth College.
Development of the clinical prediction rule
Two different techniques, linear discriminant analysis (LDA) and logistic regression (LR), were considered. Both techniques are established methods of generating prediction rules. The slight differences in the techniques allow each to occasionally outperform the other. In theory, if the feature covariance matrices for each of two sets of patients are unequal, there may be a slight advantage to using LR over LDA. However, empirical evidence suggests that this covariance matrix test is not always predictive [24,25]. We therefore computed clinical prediction rules using both LDA and LR, and compared their performance.
To remain consistent with previous work, we defined a positive outcome as not surviving to discharge [26]. A true positive is a patient who does not survive to discharge who was predicted not to survive. The specificity measures the percentage of patients who lived that were predicted to live. The sensitivity measures the percentage of patients who did not survive who were predicted to not survive. We maximized specificity.
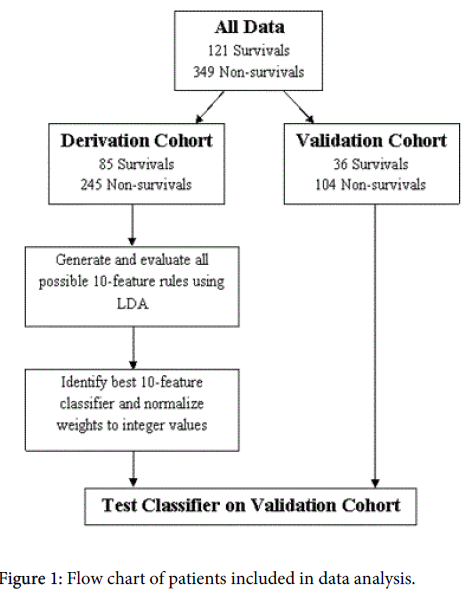
The dataset consisting of 470 patients was divided into derivation and validation cohorts. A random sample of 330 patients was assigned to the derivation cohort, which was used for developing the prediction rule (Figure 1). After we constructed the model, we evaluated its performance on the validation cohort.
Twenty-six of thirty initially collected features were used with LDA to create the clinical prediction rule. S3 gallop and abnormal PaCO2 were excluded due to insufficient data. Independence or dependence with ADLs were removed after analysis revealed that the act of assessing ADL status, not the status itself, was predictive of survival. Using the derivation cohort, a search over all possible 10-feature combinations of the 26 features (approximately 5.3 million combinations) was performed. Each set of 10-features was evaluated by performing 1000 splits of the derivation cohort into a training set containing 90% of the patients in the cohort and a testing set containing the remaining 10%. For each split, LDA was used to generate significance weights for each feature and a temporary threshold was chosen to identify all survivors on the training set. The choice to identify all survivors compromised sensitivity but resulted in a desired low false-positive rate. The average performance over the 1000 randomly chosen test sets was used as a criterion to rank each set of 10 features.
The best performing 10-feature rule was identified and normalized to create an integer classifier with all feature weights falling between 0 and 5 (inclusive). To increase the usability and adaptability of the tool by the healthcare team, all initially negative weights were converted to positive weights by replacing each feature with a negative weight with an equivalent ‘absent’ feature with the same weight magnitude, albeit positive (e.g., angina pectoris had an initial weight of -4, so we added a feature “no angina pectoris” with a weight of +4). This weight inversion required that the thresholds be shifted by an equivalent amount. The final thresholds reported in this study (≤7 and ≥9) were manually selected. Patients with a score of 7 or lower are likely to survive to discharge, patients with a score of 9 or above are not likely to survive to discharge, and no prediction is made for patients who score between the thresholds. The performance of this rule was evaluated against the validation cohort and the results were compared against other clinical prediction rules.
We also considered the technique of LR. The entire dataset was analyzed with the logistic regression functions as implemented in the statistical computing software R [27]. The binomial logit model was used and calculations took four Fisher Scoring iterations. Four features were identified with p-values less than 0.05. The classifier was normalized to integer weights and thresholds were manually selected to optimize sensitivity and specificity. Since the data was not divided into derivation and validation cohorts, the performance of LR was judged using the entire dataset. Given that we are trying to optimize specificity, it is most fair to compare the LDA model to an LR model with threshold chosen to approximately match the specificity of the LDA-derived rule.
Results
Characteristics of the study population
A total of 470 individual attempts at CPR after cardiopulmonary arrest were reviewed. Overall, 25.7% survived to hospital discharge. In the derivation cohort, the mean age was 67.2 years (Standard Deviation, 14.8 years); 58.5% were men; and 85 of 330 or 25.8% survived to hospital discharge. In the validation cohort, the mean age was 67.0 (Standard Deviation, 15.7 years); 51.4% were men; and 36 of 140 or 25.7% survived to hospital discharge. No significant differences in baseline characteristics between the two cohorts were observed (Table 1).
| Number of Patients | % of Patients | |||||
|---|---|---|---|---|---|---|
| Characteristic | Derivation Cohort | Validation Cohort | Derivation Cohort | Validation Cohort | P-Value | Chi-Square Score |
| Male Sex | 193 | 72 | 58% | 51% | 0.158 | 1.990 |
| Age >70 | 148 | 67 | 45% | 48% | 0.549 | 0.359 |
| Independent ADLs | 160 | 76 | 48% | 54% | 0.250 | 1.323 |
| Not-Completely-Independent ADLs | 128 | 47 | 39% | 34% | 0.285 | 1.145 |
| PMH CVA | 37 | 15 | 11% | 11% | 0.875 | 0.025 |
| CRI/ ESRD | 71 | 29 | 22% | 21% | 0.846 | 0.038 |
| Angina Pectoris | 102 | 36 | 31% | 26% | 0.258 | 1.279 |
| CHF (III or IV) | 98 | 36 | 30% | 26% | 0.382 | 0.765 |
| PMH MI | 73 | 24 | 22% | 17% | 0.223 | 1.487 |
| Cancer | 82 | 32 | 25% | 23% | 0.645 | 0.212 |
| Cirrhosis | 9 | 6 | 3% | 4% | 0.379 | 0.773 |
| Dementia | 13 | 4 | 4% | 3% | 0.566 | 0.330 |
| Respiratory Insufficiency | 114 | 47 | 35% | 34% | 0.839 | 0.041 |
| Immunocompromised | 8 | 4 | 2% | 3% | 0.786 | 0.074 |
| Sepsis | 25 | 9 | 8% | 6% | 0.661 | 0.193 |
| Pneumonia | 46 | 19 | 14% | 14% | 0.916 | 0.011 |
| Recent MI | 90 | 41 | 27% | 29% | 0.656 | 0.198 |
| CVA | 14 | 8 | 4% | 6% | 0.490 | 0.477 |
| Coma | 13 | 3 | 4% | 2% | 0.326 | 0.965 |
| Ventilation | 145 | 71 | 44% | 51% | 0.178 | 1.817 |
| Hypotension | 94 | 35 | 28% | 25% | 0.439 | 0.599 |
| S3 Gallop | 1 | 0 | 0% | 0% | 0.514 | 0.425 |
| Oliguria | 4 | 2 | 1% | 1% | 0.848 | 0.037 |
| Pulmonary Edema | 73 | 37 | 22% | 26% | 0.313 | 1.017 |
| Abnl BUN | 48 | 23 | 15% | 16% | 0.602 | 0.272 |
| Abnl Cr | 136 | 51 | 41% | 36% | 0.333 | 0.939 |
| Abnl pH | 75 | 28 | 23% | 20% | 0.513 | 0.427 |
| Abnl PaCO2 | 95 | 38 | 29% | 27% | 0.717 | 0.131 |
| Abnl PaO2 | 23 | 11 | 7% | 8% | 0.734 | 0.115 |
| AbnlBicarb | 31 | 11 | 9% | 8% | 0.593 | 0.285 |
| Deceased | 245 | 104 | 74% | 74% | 0.992 | 0.000 |
Table 1: Baseline characteristics of the derivation and validation cohorts
In chi-square univariate analysis of the derivation cohort, the presence of angina pectoris, hypotension, abnormal pH, and abnormal bicarbonate were the only characteristics that had a statistically significant difference between patients who survived to discharge and those who did not (Table 2). Angina pectoris was found to be protective while hypotension, abnormal pH, and abnormal bicarbonate were significant risk factors for non-survival to hospital discharge. There was no significant association between mortality and the other variables.
| Number of Patients | % of Patients | |||||
|---|---|---|---|---|---|---|
| Characteristic | Survived | Deceased | Survived | Deceased | P-Value | Chi-Square Score |
| Male Sex | 57 | 136 | 67% | 56% | 0.063 | 3.466 |
| Age >70 | 34 | 114 | 40% | 47% | 0.297 | 1.088 |
| Independent ADLs | 41 | 119 | 48% | 49% | 0.957 | 0.003 |
| Not-Completely-Independent ADLs | 38 | 90 | 45% | 37% | 0.194 | 1.689 |
| PMH CVA | 9 | 28 | 11% | 11% | 0.832 | 0.045 |
| CRI/ ESRD | 22 | 49 | 26% | 20% | 0.255 | 1.293 |
| Angina Pectoris | 38 | 64 | 45% | 26% | 0.001 | 10.205 |
| CHF (III or IV) | 32 | 66 | 38% | 27% | 0.063 | 3.466 |
| PMH MI | 19 | 54 | 22% | 22% | 0.952 | 0.004 |
| Cancer | 20 | 62 | 24% | 25% | 0.744 | 0.107 |
| Cirrhosis | 1 | 8 | 1% | 3% | 0.308 | 1.038 |
| Dementia | 4 | 9 | 5% | 4% | 0.673 | 0.178 |
| Respiratory Insufficiency | 36 | 78 | 42% | 32% | 0.079 | 3.086 |
| Immunocompromised | 3 | 5 | 4% | 2% | 0.442 | 0.591 |
| Sepsis | 5 | 20 | 6% | 8% | 0.493 | 0.469 |
| Pneumonia | 12 | 34 | 14% | 14% | 0.956 | 0.003 |
| Recent MI | 24 | 66 | 28% | 27% | 0.817 | 0.053 |
| CVA | 1 | 13 | 1% | 5% | 0.104 | 2.649 |
| Coma | 2 | 11 | 2% | 4% | 0.383 | 0.761 |
| Ventilation | 35 | 110 | 41% | 45% | 0.551 | 0.355 |
| Hypotension | 16 | 78 | 19% | 32% | 0.022 | 5.246 |
| S3 Gallop | 0 | 1 | 0% | 0% | 0.555 | 0.348 |
| Oliguria | 0 | 4 | 0% | 2% | 0.236 | 1.405 |
| Pulmonary Edema | 19 | 54 | 22% | 22% | 0.952 | 0.004 |
| Abnl BUN | 11 | 37 | 13% | 15% | 0.626 | 0.237 |
| Abnl Cr | 34 | 102 | 40% | 42% | 0.792 | 0.069 |
| Abnl pH | 9 | 66 | 11% | 27% | 0.002 | 9.606 |
| AbnlPaCO2 | 24 | 71 | 28% | 29% | 0.896 | 0.017 |
| AbnlPaO2 | 2 | 21 | 2% | 9% | 0.052 | 3.764 |
| AbnlBicarb | 3 | 28 | 4% | 11% | 0.031 | 4.626 |
Table 2: Univariate analysis of clinical characteristics and survival in the derivation cohort.
The four features in bold demonstrated a statistically significant difference between patients that did and did not survive (via chisquare analysis at the 0.05 level).
Description of the clinical prediction rule
We define the Dartmouth Score as the best ten-feature clinical prediction rule generated using LDA (Table 3). The rule includes both protective features and those indicative of non-survival. It achieves a specificity of 82.4% and a sensitivity of 42.7% on the validation cohort. In contrast, the LR derived rule obtained when the threshold is set to approximate the same specificity (83%) achieves a lower sensitivity and a higher false negative rate than the Dartmouth Score (Table 4).
| Clinical feature | Weighted score |
|---|---|
| Age>70 | 2 |
| No Angina Pectoris | 4 |
| No Dementia | 1 |
| No Respiratory Insufficiency | 2 |
| CVA | 5 |
| Hypotension | 3 |
| AbnlPaO2 | 3 |
| AbnlBicarb | 3 |
| Coma | 2 |
| Cancer | 1 |
Table 3: The Dartmouth Score ten feature clinical prediction rule.
| Performance of logistic regression classifier | |
| Specificity | 0.83 |
| Sensitivity | 0.33 |
| FNrate | 0.67 |
| LRP | 1.99 |
| LRN | 0.8 |
| PPV | 0.85 |
| NPV | 0.3 |
| FNrate: False Negative Rate, LRP: Likelihood ratio of a positive result, LRN: Likelihood ratio of a negative result, PPV: Positive Predictive Value, NPV: Negative Predictive Value | |
Table 4: Test characteristics of Logistic Regression Analysis classifier.
In the Dartmouth Score, the features of age (greater than 70 years of age), history of cancer, previous cardiovascular accident or CVA, presence of coma, hypotension, abnormal PaO2, and abnormal bicarbonate were identified as the best predictors of non-survival. Angina, dementia, and chronic respiratory insufficiency were selected as protective features.
Development of thresholds for utilization
Setting the survival threshold at ≤7 and the non-survival threshold at ≥9 allowed us to predict the outcome in 88% of patients in our validation cohort. For 12% of the patients there was insufficient information, given the clinical features, to make a prediction. In these instances, rather than force a prediction, the rule states that the outcome is uncertain.
Comparison with other scores
We compared our rule’s performance to the performance of previously published clinical prediction rules (PAM [19], PAR [20], MPI [21]) on our testing cohort (Table 5). Compared with previously published rules, our score achieves the highest sensitivity, and is most predictive, having the highest positive and negative prediction values, while maintaining relatively similar specificity and false negative rates. Interestingly, the previously published morbidity scores PAM, PAR, MPI do not show a statistically significant difference between the scores of those who survive to hospital discharge and those who do not (P-values for χ2 for MPI 0.10, PAM 0.38, PAR 0.55). There is a statistically significant correlation between the Dartmouth Scores (DS) of patients who are discharged alive and those who are not (P-value for χ2 for DS is 0.01). It is important to note that despite our use of separate derivation and validation cohorts, one would reasonably expect our rule to outperform previous rules on our dataset given that our patient demographics are likely slightly different from those used to create previous rules. Follow-up studies will be informative with respect to how well our rule generalizes.
| Test | ||
| PAM | Specificity | 0.78 |
| Sensitivity | 0.3 | |
| FNrate | 0.7 | |
| LRP | 1.34 | |
| LRN | 0.9 | |
| PPV | 0.8 | |
| NPV | 0.28 | |
| P-value | 0.382 | |
| PAR | Specificity | 0.86 |
| Sensitivity | 0.18 | |
| FNrate | 0.82 | |
| LRP | 1.32 | |
| LRN | 0.95 | |
| PPV | 0.79 | |
| NPV | 0.27 | |
| P-value | 0.548 | |
| MPI | Specificity | 0.89 |
| Sensitivity | 0.24 | |
| FNrate | 0.76 | |
| LRP | 2.16 | |
| LRN | 0.86 | |
| PPV | 0.86 | |
| NPV | 0.29 | |
| P-value | 0.099 | |
| DS Cutoff 7, 9 | Specificity | 0.82 |
| Sensitivity | 0.43 | |
| FNrate | 0.57 | |
| LRP | 2.42 | |
| LRN | 0.7 | |
| PPV | 0.86 | |
| NPV | 0.35 | |
| P-value | 0.01 | |
| FNrate: False Negative Rate, LRP: Likelihood ratio of a positive result, LRN: Likelihood ratio of a negative result, PPV: Positive Predictive Value, NPV: Negative Predictive Value, P-value: chi-square p-value for clinical prediction vs. actual outcome. | ||
Table 5: Comparison of test characteristics The Dartmouth Score with other published scores.
Discussion
Discussion of code status has become a routine part of many hospital admissions, but is still performed without sufficient discussion of or knowledge about the patient’s chance of surviving resuscitation. We used two statistical techniques to create a simple but clinically useful prediction tool. The Dartmouth Score uses information easily obtainable on admission to provide physicians and their patient’s individualized information about their probability of survival after in-hospital cardiopulmonary arrest and attempted resuscitation.
Our dataset is the largest to date used to develop a clinical prediction rule for non-survival after in-hospital cardiac arrest. We used standardized definitions of medical diagnoses, physical findings and laboratory tests to determine each individual’s features. We combined our comprehensive retrospective chart review with rigorous computational methods to create a relatively sensitive and specific score with a statistically significant correlation between predicted and actual outcomes. We attempted to maximize specificity since most physicians would prefer to attempt several unsuccessful resuscitations rather than risk withholding resuscitation from a single patient in whom it would be successful. Our two-threshold prediction rule is more sensitive than other previously published scores. Our prediction rule has the additional advantage that it can indicate when there is insufficient information to make a prediction. Given the complexity of many patients’ medical state, the identification of a ‘grey zone’ is clinically reasonable.
As mentioned above, our study population (derivation plus validation cohorts), had an average of 25.7% of patients survive CPR to hospital discharge. The Dartmouth Score was able to provide more patient-specific information about chances of surviving to hospital discharge. Patients with a score of 7 or lower on the Dartmouth Score had a 38.5% chance of surviving to hospital discharge after CPR, while those patients with a score of 9 or higher had a less than 15% chance of surviving to hospital discharge after CPR. This information may be helpful to clinicians when attempting to translate a patient’s Dartmouth Score into actionable information for a patient and their family.
Our prediction rule has reasonable face validity in addition to our successful empirical validation. The multifaceted nature of the relevant medical phenomena makes it difficult to fully rationalize the inclusion of each clinical variable into our prediction rule. In the next few paragraphs we propose potential medical justification to support our rule’s inclusion of several clinical variables. These ideas are intended to spur discussion and are not meant as definitive explanations.
Many of the features of our prediction rule (age>70 years, angina pectoris, dementia, CVA, cancer, comatose state and hypotension) are included as risk factors in previous mortality scores (Table 6). Angina pectoris is included as a risk factor in PAM and MPI but is a protective factor in our study. This difference may be because of how angina pectoris was defined; we were more rigorous in our definition of angina pectoris and did not include unstable angina as a feature. Chronic, stable angina pectoris may be a surrogate marker for VT arrest, which is known to lead to better survival rates than other forms of cardiac arrest [28].
| Comparison of Dartmouth Score (DS) with PAM, PAR and MPI scores | ||||
| DS | PAM | PAR | MPI | |
| Age > 70 | 2 | 2 | 1 | |
| Angina Pectoris | 1 | 1 | ||
| No Angina Pectoris | 4 | |||
| Dementia | 2 | |||
| No Dementia | 1 | |||
| Respiratory Insufficiency | ||||
| No Respiratory Insufficiency | 2 | |||
| CVA | 5 | 1 | 2 | |
| Hypotension | 3 | 3 | 3 | |
| Abnl PaO2 | 3 | |||
| AbnlBicarb | 3 | |||
| Coma | 2 | 1 | 1 | |
| Cancer | 1 | 3 | 2 | |
| Metastatic Cancer | 10 | |||
| Non-Metastatic Cancer | 3 | |||
| Homebound | 3 | 5 | 2 | |
| Heart Failure | 1 | 1 | ||
| Cirrhosis | 1 | |||
| Sepsis | 1 | 5 | 1 | |
| Pneumonia | 3 | 3 | 2 | |
| Acute MI | 1 | -2 | 1 | |
| Ventilated | 1 | 1 | ||
| Gallop | 1 | 1 | ||
| Oliguria | 1 | 1 | ||
| Abnl Creatinine | 3 | 3 | 2 | |
| Cutoff | ≤7 and ≥9 | >6 | >7 | >6 |
Table 6: Comparison of the Dartmouth Score (DS) with previously published decision rules.
Dementia is included as a risk factor in MPI but is protective in our study. Our study had far fewer patients with dementia than expected (3.6% of the patients in our sample had dementia, compared to a national prevalence of dementia in the elderly of 13.9% [29]). We suspect that our finding reflects that only a subsection of healthier demented patients undergo CPR as increased use of advanced directives and living wills prevent resuscitation in patients with endstage dementia.
Chronic respiratory insufficiency is unique to our score. Patients with respiratory insufficiency are more likely to be exposed to theophylline and beta-adrenergic agonists, which can cause ventricular ectopy including ventricular tachycardia. In addition, COPD is associated with prolonged QT which can degenerate into torsades de pointes. Increased survival after CPR for patients with chronic respiratory insufficiency may reflect these more treatable arrhythmias.
Abnormal laboratory results of partial pressure of oxygen in arterial blood (PaO2) and serum bicarbonate are also unique to our score. Review of patients with abnormal PaO2 found hypoxia significant enough to require ventilation, and is therefore in line with prior scores use of indicators of acute respiratory insufficiency (ventilatordependent and pneumonia) as risk factors for non-survival. Review of patients with abnormal serum bicarbonate indicated that 91% of patients with abnormal levels suffered from severe acidemia, with the remaining patients having chronic respiratory acidosis. Low serum bicarbonate may thus be a proxy for organ infarction (lactic acidosis), diabetic ketoacidosis, renal failure, or fatal toxic ingestions.
Poor functional status has been shown to correlate with poor outcomes in other studies. We had hoped to incorporate functional status in our score, but the lack of data reflecting functional status in the sicker, intensive-care based population, prevented us from doing so.
Our rule was derived using data from a patient population that underwent CPR. Patients with DNR orders who did not undergo CPR were not captured in our study. Hence, our rule is biased towards patients who opted against a DNR order.
The Dartmouth Score was developed based on data collected at a rural, academic, tertiary-care center serving a largely Caucasian population. Differences in survival after CPR based on location and size of hospital as well as race have been documented [3]. The Dartmouth Score should be evaluated outside our institution. The score was based on data collected retrospectively and validated with an independent validation cohort. Due to the rarity of in-hospital cardiopulmonary arrest, prospective validation of the tool is impractical. Validation retrospectively at multiple centers would provide further evidence as to the accuracy and clinical utility of The Dartmouth Score. Our score may be clinically useful after it is validated by other cohorts.
The complex physiologic process of cardiac arrest, resuscitation, and recovery makes it unlikely that a handful of features will be able to predict outcomes with extremely high accuracy. However, the Dartmouth Score may be a useful addition to medical expertise and clinical judgment in evaluating and communicating an individual’s probability of survival after in-hospital cardiopulmonary arrest. Our model may provide helpful information to guide physicians and patients in shared decision making on this important subject.
Acknowledgements
We are indebted to the Department of Medicine, Dartmouth-Hitchcock Medical Center, for providing funding for data collection. Satyam Merja was funded by Natural Sciences and Engineering Research Council of Canada’s (NSERC) Undergraduate Student Research Awards Program and he performed data and statistical analysis. Other than providing financial support, NSERC did not have any role or involvement with the study.
References
- Kouwenhoven WB, Jude JR, Knickerbocker GG (1960) Closed-chest cardiac massage. See comment in PubMed Commons below JAMA 173: 1064-1067.
- Dans PE, Nevin KL, Seidman CE, McArthur JC, Kariya ST (1985) Inhospital CPR 25 years later: why has survival decreased? South Med J 78: 1174-1178.
- Ehlenbach WJ, Barnato AE, Curtis JR, Kreuter W, Koepsell TD, et al. (2009) Epidemiologic study of in-hospital cardiopulmonary resuscitation in the elderly. N Engl J Med 361: 22-31.
- Mirza A, Kad R, Ellison NM(2005) Cardiopulmonary resuscitation is not addressed in the admitting medical records for the majority of patients who undergo CPR in the hospital. American Journal of Hospice & Palliative Medicine22: 20-25.
- Krumholz HM, Phillips RS, Hamel MB (1998) Resuscitation preferences among patients with severe congestive heart failure: results from the SUPPORT project. Circulation98: 648-55.
- Hofmann JC, Wenger NS, Davis RB, Teno J, Connors AF Jr, et al. (1997) Patient preferences for communication with physicians about end-of-life decisions. SUPPORT Investigators. Study to Understand Prognoses and Preference for Outcomes and Risks of Treatment. Ann Intern Med 127: 1-12.
- Phillips RS, Wenger NS, Teno J, Oye RK, Youngner S, et al. (1996) Choices of seriously ill patients about cardiopulmonary resuscitation: correlates and outcomes. SUPPORT Investigators. Study to Understand Prognoses and Preferences for Outcomes and Risks of Treatments. Am J Med 100: 128-137.
- Haidet P, Hamel MB, Davis RB (1998) Outcomes, preferences for resuscitation, and physician-patient communication among patients with metastatic colorectal cancer. American Journal of Medicine105: 222-229.
- Hakim RB, Teno JM, Harrell FE Jr, Knaus WA, Wenger N, et al. (1996) Factors associated with do-not-resuscitate orders: patients' preferences, prognoses, and physicians' judgments. SUPPORT Investigators. Study to Understand Prognoses and Preferences for Outcomes and Risks of Treatment. Ann Intern Med 125: 284-293.
- Paris BE, Carrion VG, Meditch JS Jr, Capello CF, Mulvihill MN (1993) Roadblocks to do-not-resuscitate orders. A study in policy implementation. Arch Intern Med 153: 1689-1695.
- Eliasson AH, Parker JM, Shorr AF, Babb KA, Harris R, et al. (1999) Impediments to writing do-not-resuscitate orders. Arch Intern Med 159: 2213-2218.
- Christakis NA, Iwashyna TJ (1998) Attitude and self-reported practice regarding prognostication in a national sample of internists. Arch Intern Med 158: 2389-2395.
- Miller DL, Gorbien MJ, Simbartl LA, Jahnigen DW (1993) Factors influencing physicians in recommending in-hospital cardiopulmonary resuscitation. Arch Intern Med 153: 1999-2003.
- Schonwetter RS, Walker RM, Kramer DR, Robinson BE (1993) Resuscitation decision making in the elderly: the value of outcome data. J Gen Intern Med 8: 295-300.
- Murphy DJ, Burrows D, Santilli S, Kemp AW, Tenner S, et al. (1994) The influence of the probability of survival on patients' preferences regarding cardiopulmonary resuscitation. N Engl J Med 330: 545-549.
- van Walraven C, Forster AJ, Parish DC, Dane FC, Chandra KM, et al. (2001) Validation of a clinical decision aid to discontinue in-hospital cardiac arrest resuscitations. JAMA 285: 1602-1606.
- Brindley PG, Markland DM, Mayers I, Kutsogiannis DJ (2002) Predictors of survival following in-hospital adult cardiopulmonary resuscitation. CMAJ 167: 343-348.
- Tok D, Keles GT, Toprak V, Topcu I.(2004) Assessment of in-hospital cardiopulmonary resuscitation using Utstein Template in a University hospital. Tohoku J Exp Med202: 265-273.
- George AL Jr, Folk BP 3rd, Crecelius PL, Campbell WB (1989) Pre-arrest morbidity and other correlates of survival after in-hospital cardiopulmonary arrest. Am J Med 87: 28-34.
- Ebell MH (1992) Prearrest predictors of survival following in-hospital cardiopulmonary resuscitation: a meta-analysis. J FamPract 34: 551-558.
- Dautzenberg PL, Broekman TC, Hooyer C, Schonwetter RS, Duursma SA (1993) Review: patient-related predictors of cardiopulmonary resuscitation of hospitalized patients. Age Ageing 22: 464-475.
- Cummins RO, Chamberlain D, Hazinski MF (1997) Recommended Guidelines for Reviewing, Reporting, and Conducting Research on In-Hospital Resuscitation: The In-Hospital `Utstein Style' : A Statement for Healthcare Professionals From the American Heart Association, the European Resuscitation Council, the Heart and Stroke Foundation of Canada, the Australian Resuscitation Council, and the Resuscitation Councils of Southern Africa. Circulation95 :2213-39.
- Ballew KA, Philbrick JT, Caven DE, Schorling JB (1994) Predictors of survival following in-hospital cardiopulmonary resuscitation. A moving target. Arch Intern Med 154: 2426-2432.
- Lei P, Koehly L (2003) Linear Discriminant Analysis versus Logistic Regression: A Comparison of Classification Errors in the Two-Group Case. The Journal of Experimental Education72:25-49.
- Meshbane A, Morris JD (1996) Predictive discriminant analysis versus logistic regression in two-group classification problems. In: American Educational Research Association. New York
- Bowker L, Stewart K (1999) Predicting unsuccessful cardiopulmonary resuscitation (CPR): a comparison of three morbidity scores. Resuscitation 40: 89-95.
- Dean CB, Nielsen JD (2007) Generalized linear mixed models: a review and some extensions. Lifetime Data Anal 13: 497-512.
- Marwick TH, Case CC, Siskind V, Woodhouse SP (1991) Prediction of survival from resuscitation: a prognostic index derived from multivariate logistic model analysis. Resuscitation 22: 129-137.
- Plassman BL, Langa KM, Fisher GG, Heeringa SG, Weir DR, et al. (2007) Prevalence of dementia in the United States: the aging, demographics, and memory study. Neuroepidemiology 29: 125-132.
Relevant Topics
- Caregiver Support Programs
- End of Life Care
- End-of-Life Communication
- Ethics in Palliative
- Euthanasia
- Family Caregiver
- Geriatric Care
- Holistic Care
- Home Care
- Hospice Care
- Hospice Palliative Care
- Old Age Care
- Palliative Care
- Palliative Care and Euthanasia
- Palliative Care Drugs
- Palliative Care in Oncology
- Palliative Care Medications
- Palliative Care Nursing
- Palliative Medicare
- Palliative Neurology
- Palliative Oncology
- Palliative Psychology
- Palliative Sedation
- Palliative Surgery
- Palliative Treatment
- Pediatric Palliative Care
- Volunteer Palliative Care
Recommended Journals
- Journal of Cardiac and Pulmonary Rehabilitation
- Journal of Community & Public Health Nursing
- Journal of Community & Public Health Nursing
- Journal of Health Care and Prevention
- Journal of Health Care and Prevention
- Journal of Paediatric Medicine & Surgery
- Journal of Paediatric Medicine & Surgery
- Journal of Pain & Relief
- Palliative Care & Medicine
- Journal of Pain & Relief
- Journal of Pediatric Neurological Disorders
- Neonatal and Pediatric Medicine
- Neonatal and Pediatric Medicine
- Neuroscience and Psychiatry: Open Access
- OMICS Journal of Radiology
- The Psychiatrist: Clinical and Therapeutic Journal
Article Tools
Article Usage
- Total views: 15023
- [From(publication date):
May-2015 - Aug 29, 2025] - Breakdown by view type
- HTML page views : 10414
- PDF downloads : 4609